В закрытом сосуде объемом 20 л находится 5 моль кислорода

8. Молекулярно-кинетическая теория
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
В сосуде объёмом 2 л находится 10 г идеального газа при давлении 1 атм. и температуре 300 К. Во втором сосуде объёмом 4 л находится 20 г того же газа при давлении 2 атм. Чему равна температура газа во втором сосуде? (Ответ дайте в кельвинах.)
Уравнение состояния газа: [pV=nu RT=dfrac{m}{mu}RT] где (p) — давление газа, (V) — объем, занимаемый газом, (nu) — количество вещества, (R) — универсальная газовая постоянная, (T) — температура газа, (m) — масса газа, (mu) — молярная масса газа.
Для первого сосуда: [p_1V_1=dfrac{m_1}{mu}RT_1] Для второго сосуда: [p_2V_2=dfrac{m_2}{mu}RT_2] Поделим уравнения друг на друга: [dfrac{p_1V_1}{p_2V_2}=frac{m_1T_1}{m_2T_2}] [T_2=T_1cdotdfrac{m_1}{m_2}cdotdfrac{V_2}{V_1}cdotdfrac{p_2}{p_1}=300text{ К}cdotdfrac{1}{2}cdot2cdot2=600 text{ К}]
Ответ: 600
При уменьшении абсолютной температуры газа на 300 К давление уменьшилось в 5 раз. Какова начальная температура газа, если в ходе эксперимента количество вещества уменьшилось втрое, а объём оставался постоянным? (Ответ дайте в кельвинах.)
Запишем уравнение Менделеева-Клапейрона для первого и второго состояния: [begin{cases}
p_1 V=nu_1 R T_1\
p_2 V=nu_2 R T_2
end{cases}] где (p_1) и (p_2) — давления газа в первом и втором состояниях, V — объём газа, (nu_1) и (nu_2)— количество вещества в первом и втором состояниях, (R) — универсальная газовая постоянная, (T_1) и (T_2) — абсолютная температура в первом и втором состояниях.
Поделив одно уравнение на другое, получим: [dfrac{p_1}{p_2} = dfrac{nu_1 T_1}{nu_2 T_2}] Так как (nu_1 = 3nu_2) и (p_1 = 5p_2), то: [dfrac{5p_2}{p_2} = dfrac{3nu_2cdot T_1}{nu_2cdot T_2}
hspace{0,4 cm} Rightarrow hspace{0,4 cm}
5=dfrac{3T_1}{T_2}
hspace{0,4 cm} Rightarrow hspace{0,4 cm}
5T_2 = 3T_1] Так как (T_2 = (T_1 – 200) К), то: [5(T_1 – 300text{ K}) = 3T_1
hspace{0,4 cm} Rightarrow hspace{0,4 cm}
5T_1 – 1500text{ K } = 3T_1
hspace{0,4 cm} Rightarrow hspace{0,4 cm}
2T_1 = 1500text{ K }
hspace{0,4 cm} Rightarrow hspace{0,4 cm}
T_1 = 750text{ K }]
Ответ: 750
На графиках приведены зависимости давления (p) и объема (V) от времени (t) для 1 моля идеального газа. Чему равна температура газа в момент (t) = 30 минут? (Ответ дайте в градусах Кельвина с точностью до 10 К.)
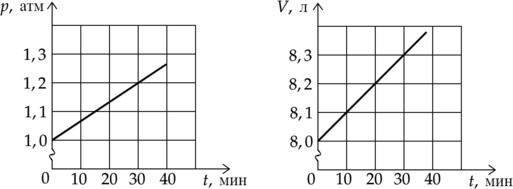
Уравнение состояния идеального газа: [displaystyle pV=nu RT,] где (p)—давление газа, (V)—объем газа, (nu) — количество вещества газа, (R) — универсальная газовая постоянная, (T) — температура. Выразим температуру газа: [T=dfrac{pV}{nu R}] Из графика найдем давление и объем в момент времени 30 мин:
(p=1,2cdot10^5) Па
(V=8,3cdot10^{-3}text{ м$^3$})
Подставим известные и найденные значения в формулу: [T=dfrac{1,2cdot10^5text{ Па}cdot8,3cdot10^{-3}text{ м$^3$}}{1text{ моль}cdot8,31text{ }dfrac{text{Дж}}{text{моль}}} approx 120 text{ К}]
Ответ: 120
В сосуде неизменного объёма находится разреженный газ в количестве 3 моль. Во сколько раз изменится давление газа в сосуде, если выпустить из него 1 моль газа, а абсолютную температуру газа уменьшить в 2 раза?
“Демоверсия 2019”
Запишем уравнение Клапейрона – Менделеева: [p1V=nu_1RT_1=3RT_1] [p_2V=nu_2RT_2=2Rdfrac{T_1}{2}=RT_1] [dfrac{p_1}{p_2}=dfrac{3RT_1}{RT_1}=3]
Ответ: 3
В сосуде неизменного объёма находится идеальный газ. Во сколько раз нужно увеличить количество газа в сосуде, чтобы после уменьшения абсолютной температуры газа в 2 раза его давление стало вдвое больше начального?
“Досрочная волна 2020 вариант 1”
Из уравнения Клапейрона –Менделеева: [pV=nu RT] чтобы давление ((p)) увеличилось в 2 раза, при уменьшении температуры ((T)) в 2 раза, количество вещества ((nu)) должно увеличится в 4 раза
Ответ: 4
В сосуде неизменного объема находится разреженный газ в количестве 4 моль. Во сколько раз нужно увеличить абсолютную температуру газа, чтобы после удаления из сосуда 3 моль газа, давление осталось неизменным?
“Основная волна 2020 ”
Уравнение Клайперона – Менделеева: [pV=nu RT] если удалить 3 моль газа, то количество вещества уменьшится в 4 раза (nu_1=dfrac{nu}{4}), следовательно, температуру надо увеличить в 4 раза.
Ответ: 4
Источник
В сосуде содержится гелий под давлением кПа. Концентрацию гелия увеличили в раза, а среднюю кинетическую энергию его молекул уменьшили в раза.
Определите установившееся давление газа.
Ответ дайте в кПа.
Это задание решали 178 раз. С ним справились 33% пользователей.
Газ, который можно считать идеальным, перешел из состояния в состояние
Определите отношение давлений газа в начальном и конечном состояниях
Масса газа постоянна.
Это задание решали 54 раза. С ним справились 26% пользователей.
На рисунке изображен процесс перехода идеального газа постоянной массы из состояния в состояние
Найдите, во сколько раз изменилась абсолютная температура газа в состоянии по сравнению с абсолютной температурой в состоянии
Это задание решали 93 раза. С ним справились 71% пользователей.
Это задание решали 42 раза. С ним справились 57% пользователей.
На рисунке изображена зависимость давления от абсолютной температуры для
постоянной массы идеального газа.
Объем газа в состоянии равен л.
Определите объем газа (в л) в состоянии
Это задание решали 58 раз. С ним справились 71% пользователей.
Это задание решали 65 раз. С ним справились 42% пользователей.
моль идеального газа изохорно нагревают на К, при этом его давление
увеличивается в раза.
Какова первоначальная абсолютная температура газа?
Это задание решали 51 раз. С ним справились 37% пользователей.
Во сколько раз увеличится значение квадрата среднеквадратичной скорости
движения молекул, если для данной массы газа его внутренняя энергия
увеличится в раза?
Это задание решали 52 раза. С ним справились 65% пользователей.
Давление идеального газа в герметичном сосуде объемом л равно кПа.
Каким будет давление (в кПа) этого газа, если объем сосуда изотермически
увеличить в раза?
Это задание решали 63 раза. С ним справились 57% пользователей.
Давление газа на стенки герметичного баллона равно кПа.
Чему будет равно давление этого газа (в кПа) при увеличении квадрата средней скорости движения молекул газа в раза?
Это задание решали 43 раза. С ним справились 77% пользователей.
В ходе эксперимента давление разреженного газа в сосуде увеличилось в раза, а средняя энергия теплового движения его молекул уменьшилась в раза.
Во сколько раз увеличилась концентрация молекул газа в сосуде?
Это задание решали 117 раз. С ним справились 22% пользователей.
В сосуде находится идеальный газ при температуре C. Концентрация молекул этого газа равна м
Определите давление (в кПа), создаваемое
газом на стенки сосуда.
Постоянная Больцмана равна Дж/К.
Это задание решали 75 раз. С ним справились 53% пользователей.
В ходе эксперимента давление разреженного газа в сосуде уменьшилось в
раза.
Во сколько раз уменьшилось среднее значения квадрата скорости
движения молекул этого газа, если его концентрация осталась неизменной?
Это задание решали 22 раза. С ним справились 41% пользователей.
Идеальный газ находится в закрытом сосуде.
Во сколько раз уменьшится давление в этом сосуде, если его наполнить другим идеальным газом, молярная масса которого в два раза больше?
Абсолютная температура и плотность газа в
сосуде не изменились.
Это задание решали 64 раза. С ним справились 77% пользователей.
При проведении опыта в сосуд постоянного объема закачали воздух и одновременно сосуд с воздухом нагрели. В конечном равновесном состоянии воздуха в сосуде абсолютная температура повысилась в раза, а его давление возросло в раза по сравнению с начальными значениями.
Во сколько раз увеличилась масса воздуха в сосуде?
Это задание решали 82 раза. С ним справились 50% пользователей.
Источник
Задача 28.
При 17°С некоторое количество газа занимает объем 580 мл. Какой объем займет это же количество газа при 100°С, если давление его останется неизменным?
Решение:
По закону Гей – Люссака при постоянном давлении объём газа изменяется прямо пропорционально абсолютной температуре (Т):

V2 – искомый объём газа;
T2 – соответствующая V2 температура;
V1 – начальный объём газа при соответствующей температуре Т1.
По условию задачи V1 = 580мл; Т1 = 290К (273 + 17 = 290) и Т2 = 373К (273 + 100 = 373). Подставляя эти значения в выражение закона Гей – Люссака, получим:

Ответ: V2 = 746мл.
Задача 29.
Давление газа, занимающего объем 2,5л, равно 121,6 кПа (912мм рт. ст.). Чему будет равно давление, если, не изменяя температуры, сжать газ до объема в 1л?
Решение:
Согласно закону Бойля – Мариотта, при постоянной температуре давление, производимое данной массой газа, обратно пропорционально объёму газа:

Обозначив искомое давление газа через Р2, можно записать:

Ответ: Р2 = 304кПа (2280мм.рт.ст.).
Задача 30. На сколько градусов надо нагреть газ, находящийся в закрытом сосуде при 0 °С, чтобы давление его увеличилось вдвое?
Решение:
При постоянном объёме давление газа изменяется прямо пропорционально температуре:

По условию задачи Т1 = 0 °С + 273 = 273К; давление возросло в два раза: Р2 = 2Р1.
Подставляя эти значения в уравнение, находим:

Ответ: Газ нужно нагреть на 2730С.
Задача 31.
При 27°С и давлении 720 мм.рт. ст. объем газа равен 5л. Кой объем займет это же количество газа при 39°С и давлении 104кПа?
Решение:
Зависимость между объёмом газа, давлением и температурой выражается общим уравнением, объединяющим законы Гей-Люссака и Бойля-Мариотта:

где Р и V – давление и объём газа при температуре Т; Р0 и V0 – давление и объём газа при нормальных условиях. Данные задачи: V = 5л; Т = 298К (273 + 25 = 298); Р = 720 мм.рт.ст. (5,99 кПа); Р0 = 104 кПа; Т = 312К (273 + 39 = 312); Т = 273К. Подставляя данные задачи в уравнение, получим:

Ответ: V0 = 4,8л
Задача 32.
При 7°С давление газа в закрытом сосуде равно 96,0 кПа. Каким станет давление, если охладить сосуд до —33 °С?
Решение:
При постоянном объёме давление газа изменяется прямо пропорционально абсолютной температуре:

Обозначим искомое давление через Р2, а соответствующую ему температуру через Т2. По условию задачи Р1 = 96,0 кПа; Т1 = 280К (273 + 7 = 280); Т2 = 240К (273 – 33 = 240). Подставляя эти значения в уравнение, получим:

Ответ: Р2 = 82,3кПа.
Задача 33.
При нормальных условиях 1г воздуха занимает объем 773 мл. Какой объем займет та же масса воздуха при 0 °С и )и давлении, равном 93,3 кПа (700мм. рт. ст.)?
Решение:
Зависимость между объёмом газа, давлением и температурой выражается общим уравнением, объединяющим законы Гей-Люссака и Бойля-Мариотта:

где Р и V – давление и объём газа при температуре Т; Р0 и V0 – давление и объём газа при нормальных условиях. Данные задачи: Р0 = 101,325кПа; V0 = 773мл; Т0 = 298К (273 + 25 = 298); Т = 273К; Р = 93,3кПа. Подставляя данные задачи и преобразуя уравнение, получим:

Ответ: V = 769, 07 мл.
Задача 34.
Давление газа в закрытом сосуде при 12°С равно 100 кПа (750мм рт. ст.). Каким станет давление газа, если нагреть сосуд до 30°С?
Решение:
При постоянном объёме давление газа изменяется прямо пропорционально абсолютной температуре:

Обозначим искомое давление через Р2, а соответствующую ему температуру через Т2. По условию задачи Р1 = 100 кПа; Т1 = 285К (273 + 12 = 285); Т2 = 303К (273 + 30 = 303). Подставляя эти значения в уравнение, получим:

Ответ: Р2 = 106,3кПа.
Задача 35.
В стальном баллоне вместимостью 12л находится при 0°С кислород под давлением 15,2 МПа. Какой объем кислорода, находящегося при нормальных условиях можно получить из такого баллона?
Решение:
Зависимость между объёмом газа, давлением и температурой выражается общим уравнением, объединяющим законы Гей-Люссака и Бойля-Мариотта:

где Р и V – давление и объём газа при температуре Т; Р0 и V0 – давление и объём газа при нормальных условиях. Данные задачи: V = 12л; Т = 273К (273 + 0 = 2273); Р =15,2МПа); Р0 = 101,325кПа; Т0 = 298К (273 + 25 = 298). Подставляя данные задачи в уравнение, получим:

Ответ: V0 = 1,97м3.
Задача 36.
Температура азота, находящегося в стальном баллоне под давлением 12,5 МПа, равна 17°С. Предельное давление для баллона 20,3МПа. При какой температуре давление азота достигнет предельного значения?
Решение:
При постоянном объёме давление газа изменяется прямо пропорционально абсолютной температуре:

Обозначим искомое давление через Р2, а соответствующую ему температуру через Т2. По условию задачи Р1 = 12,5МПа; Т1 = 290К (273 + 17 = 290); Р2 = 20,3МПа. Подставляя эти значения в уравнение, получим:

Ответ: Т2 = 1980С.
Задача 37.
При давлении 98,7кПа и температуре 91°С некоторое количество газа занимает объем 680 мл. Найти объем газа при нормальных условиях.
Решение:
Зависимость между объёмом газа, давлением и температурой выражается общим уравнением, объединяющим законы Гей-Люссака и Бойля-Мариотта:

где Р и V – давление и объём газа при температуре Т; Р0 и V0 – давление и объём газа при нормальных условиях. Данные задачи: Р0 = 101,325кПа; V = 680мл; Т0 = 298К (273 + 25 = 298); Т = 364К (273 + 91 = 364); Р = 98,7кПа. Подставляя данные задачи и преобразуя уравнение, получим:
<

Ответ: V0 = 542,3мл.
Задача 38.
При взаимодействии 1,28г металла с водой выделилось 380 мл водорода, измеренного при 21°С и давлении 104,5кПа (784мм рт. ст.). Найти эквивалентную массу металла.
Решение:
Находим объём выделившегося водорода при нормальных условиях, используя уравнение:

где Р и V – давление и объём газа при температуре Т = 294К (273 +21 = 294); Р0 = 101,325кПа; Т0 = 273К; Р = 104,5кПа. Подставляя данные задачи в уравнение,
получим:

Согласно закону эквивалентов, массы (объёмы) реагирующих друг с другом веществ m1 и m2 пропорциональны их эквивалентным массам (объёмам):

Мольный объём любого газа при н.у. равен 22,4л. Отсюда эквивалентный объём водорода равен 22,4 : 2 = 11,2л или 11200 мл. Тогда, используя формулу закона эквивалентов, рассчитаем эквивалентную массу металла:

Ответ: mЭ(Ме) = 39,4г/моль.
Задача 39.
Как следует изменить условия, чтобы увеличение массы данного газа не привело к возрастанию его объема: а) понизить температуру; б) увеличить давление; в) нельзя подобрать условий?
Решение:
Для характеристики газа количеством вещества (n, моль) применяется уравнение РV = nRT, или – это уравнение Клапейрона-Менделеева. Оно связывает массу (m, кг); температуру (Т, К); давление (Р, Па) и объём (V, м3) газа с молярной массой (М, кг/моль).
Тогда из уравнения Клапейрона-Менделеева объём газа можно рассчитать по выражению:

Отсюда следует, что V = const, если при увеличении массы (m) газа на некоторую величину будет соответственно уменьшена температура (T) системы на некоторое необходимое значение. Объём системы также не изменится при постоянной температуре, если при увеличении массы (m) газа на некоторую величину будет соответственно увеличено давление (P) системы на необходимую величину.
Таким образом, при увеличении массы газа объём системы не изменится, если понизить температуру системы или же увеличить давление в ней на некоторую величину.
Ответ: а); б).
Задача 40.
Какие значения температуры и давления соответствуют нормальным условиям для газов: а) t = 25 °С, Р = 760 мм. рт. ст.; б) t = 0 °С, Р = 1,013 • 105Па; в) t = 0°С, Р = 760 мм. рт. ст.?
Решение:
Состояние газа характеризуется температурой, давлением и объёмом. Если температура газа равна 0 °С (273К), а давление составляет 101325 Па (1,013 • 105) или 760 мм. рт. ст., то условия, при которых находится газ, принято считать нормальными.
Ответ: б); в).
Источник
В данной работе предлагается определенный подход к классификации и способам решения задач на газовые законы. Такой подход позволит быстро сориентироваться в большом количестве задач на свойства газов и применить к ним те или иные приемы решения.
Основные теоретические сведения
Состояние газа характеризуется совокупностью трех физических величин или термодинамических параметров:объемом газа V, давлением Р и температурой Т. Состояние газа, при котором эти параметры остаются постоянными считают равновесным состоянием.В этом состоянии параметры газа связаны между собой уравнением состояния. Самый простой вид уравнение состояния имеет для идеального газа. Идеальным газом называют газ, молекулы которого не имеют размеров (материальные точки) и взаимодействуют друг с другом лишь при абсолютно упругих соударениях (отсутствует межмолекулярное притяжение и отталкивание). Реальные газы тем точнее подчиняются законам идеальных газов, чем меньше размеры их молекул (т.е. газ одноатомный), и чем больше он разряжен.
Уравнение состояния идеального газа или уравнение Менделеева-Клапейрона имеет вид:
– универсальная газовая постоянная
Из этого закона вытекает, что для двух произвольных состояний газа справедливо равенство, называемое уравнением Клапейрона:
Так же для идеальных газов имеют место следующие экспериментальные законы:
Закон Бойля — Мариотта:
Закон Гей-Люссака:
Закон Шарля:
Если в сосуде находится смесь нескольких газов, не вступающих друг с другом в химические реакции, то результирующее давление определяется по закону Дальтона: давление смеси равно сумме давлений, производимых каждым газом в отдельности, как если бы он один занимал весь сосуд.
Р = Р1 + Р2 +… + РN
Задачи, решение которых основывается на данных уравнениях, можно разделить на две группы:
§ задачи на применение уравнения Менделеева-Клапейрона.
- задачи на газовые законы.
ЗАДАЧИ НА ПРИМЕНЕНИЕ УРАВНЕНИЯ МЕНДЕЛЕЕВА-КЛАПЕЙРОНА.
Уравнение Менделеева-Клапейрона применяют тогда, когда
I. дано только одно состояние газа изадана масса газа (или вместо массы используют количество вещества или плотность газа).
II. масса газа не задана, но она меняется, то есть утечка газа или накачка.
При решении задач на применение равнения состояния идеального газа надо помнить:
1.если дана смесь газов, то уравнение Менделеева-Клапейрона записывают для каждого компонента в отдельности.Связь между парциальными давлениями газов, входящих в смесь и результирующим давлением смеси, устанавливается законом Дальтона.
2.если газ меняет свои термодинамические параметры или массу, уравнение Менделеева-Клапейрона записывают для каждого состояния газа в отдельности и полученную систему уравнений решают относительно искомой величины.
P.S.
§ Необходимо пользоваться только абсолютной температурой и сразу же переводить значения температуры по шкале Цельсия в значения по шкале Кельвина.
§ В задачах, где рассматривается движение сосуда с газом (пузырька воздуха, воздушного шара) к уравнению газового состояния добавляют уравнения механики.
§ если между газами происходит реакция, то надо составить уравнение реакции и определить продукты реакции
ПЕРВЫЙ ТИП ЗАДАЧ: НЕТ ИЗМЕНЕНИЯ МАССЫ
Определить давление кислорода в баллоне объемом V = 1 м3 при температуре t=27 °С. Масса кислорода m = 0,2 кг.
| V = 1 м3 μ = 0,032кг/моль m = 0,2 кг t=27 °С | Т=300К | Записываем уравнение Менделеева-Клапейрона и находим из него давление, производимое газом: |
| Р-? |
Баллон емкостью V= 12 л содержит углекислый газ. Давление газа Р = 1 МПа, температура Т = 300 К. Определить массу газа.
| V = 12 л μ =0,044кг/моль Т=300К Р =1 МПа | 0,012м3 1∙106Па | Записываем уравнение Менделеева-Клапейрона и находим массу газа |
| m -? |
При температуре Т = 309 К и давлении Р = 0,7 МПа плотность газа ρ = 12 кг/м3. Определить молярную массу газа.
| V = 12 л Т=309К Р =0,7 МПа ρ = 12 кг/м3 | 0,012м3 0,7∙106Па | Записываем уравнение Менделеева-Клапейрона Так как масса газа может быть определена через плотность газа и его объем имеем: |
| μ -? | ||
Отсюда находим молярную массу газа: | ||
Какова плотность водорода при нормальном атмосферном давлении и температуре 20°С.
| V = 12 л t=20°C Р =105 Па μ =0,002кг/моль | 0,012м3 T=293К | Нормальное атмосферное давление – это давление, равное 105 Па. И эту информацию запишем как данные задачи. Записываем уравнение Менделеева-Клапейрона |
| ρ -? | ||
Так как масса газа может быть определена через плотность газа и его объем имеем: Отсюда находим плотность газа: | ||
До какой температуры Т1 надо нагреть кислород, чтобы его плотность стала равна плотности водорода при том же давлении ,но при температуре Т2 = 200 К?
| Т2=200К ρ1 = ρ2 μ1 =0,032кг/моль μ2 =0,002кг/моль | Записываем уравнение Менделеева-Клапейрона для кислорода и для водорода через плотности газов: Так как по условию давление у двух газов одинаковое, то можно приравнять правые части данных уравнений: Сократим на R и на плотность ρ (по условию плотности газов равны) и найдем Т1 |
| Т1 -? | |
В сосуде объемом 4·10-3 м3 находится 0,012 кг газа при температуре 177°С. При какой температуре плотность этого газа будет равна 6·10-6 кг /см3, если давление газа остается неизменным.
Смесь газов
В баллоне объемом 25 литров находится 20г азота и 2 г гелия при 301К. Найдите давление в баллоне.
Определить плотность смеси, состоящей из 4 граммов водорода и 32 граммов кислорода при давлении 7°С и давлении 93кПа?
Сосуд емкостью 2V разделен пополам полупроницаемой перегородкой. В одной половине находится водород массой mВ и азот массой mА. В другой половине вакуум. Во время процесса поддерживается постоянная температура Т. Через перегородку может диффундировать только водород. Какое давление установиться в обеих частях сосуда?
| μа m1 = m2 = m3 = m μв μк Т | отсек №1 отсек №2 отсек №3 Диффундирует только водород. Следовательно, после завершения установочных процессов, в отсеке I будет водород, массой на |
| РI-? РII-? | |
половину меньшей, чем была, и весь азот. А во втором отсеке только половина массы водорода. Тогда для первого отсека установившееся давление равно: Для отсека II можно так же определить установившееся давление: | |
Вакуумированный сосуд разделен перегородками на три равных отсека, каждый объемом V. В средний отсек ввели одинаковые массы кислорода, азота и водорода. В результате чего давление в этом отсеке стало равно Р. Перегородка I проницаема только для молекул водорода, перегородка II проницаема для молекул всех газов. Найти давления Р1 Р2 и Р3, установившиеся в каждом отсеке, если температура газа поддерживается постоянной и равной Т.
| μа m1 = m2 = m3 = m μв μк Р | отсек №1 отсек №2 отсек №3 После диффундирования газов через перегородки в первом отсеке окажется треть массы водорода. Во втором и в третьем отсеках будет треть водорода, половина массы кислорода и половина всей массы азота. Тогда для первого отсека установившееся давление равно: |
| Р1-? Р2-? Р3-? | |
Если до диффундирования первоначальное давление во втором отсеке было Р, то можно записать: Отсюда можно найти Находим выражение для давления во втором и в третьем отсеках | |
И тогда давление в первом отсеке равно: | |
С химическими реакциями
В сосуде находится смесь азота и водорода. При температуре Т, когда азот полностью диссоциирован на атомы, давление равно Р (диссоциацией водорода можно пренебречь). При температуре 2Т, когда оба газа полностью диссоциированы, давление в сосуде 3Р. Каково отношение масс азота и водорода в смеси?
| μа μв Т1 =Т Т2 =2Т Р1=Р Р2=3Р | mв μвmа При температуре Т параметры газов в сосуде следующие: И результирующее давление в сосуде по закону Дальтона равно: |
2Т 2Т При температуре 2Т параметры газов в сосуде следующие: И результирующее давление в сосуде по закону Дальтона равно: | |
В герметично закрытом сосуде находится 1 моль неона и 2 моля водорода. При температуре Т1=300К, когда весь водород молекулярный, атмосферное давление в сосуде Р1=105 Па. При температуре Т2=3000К давление возросло до Р2=1,5∙105 Па. Какая часть молекул водорода диссоциировала на атомы?
| ν1=1 моль ν2=2 моль Т1 =300К Т2 =3000К Р1=105 Па Р2=1,5∙105 Па | При температуре Т1 давление газа в сосуде складывается из парциальных давлений двух газов и равно: При температуре Т2 давление газа равно: |
Из уравнения (1): Из первого находим объем V: | |
В закрытом баллоне находится смесь из m1= 0,50 г водорода и m2 = 8,0 г кислорода при давлении Р1= 2,35∙105 Па. Между газами происходит реакция с образованием водяного пара. Какое давление Р установится в баллоне после охлаждения до первоначальной температуры? Конденсации пара не происходит.
| V = 25 л μ1 = 2г/моль m1 = 0,5 г μ2 = 32г/моль m2 = 8 г | В сосуде будет происходить реакция водорода с кислородом с образованием воды:
|
| Р-? | Из уравнения реакции видно, что если в реакцию вступит весь водород, то кислорода только половина |
В результате образуется ν3=0,25 молей водяного пара и останется ν4= 0,125молей кислорода. По закону Дальтона результирующее давление в сосуде равно сумме парциальных давлений Так как известно, что до реакции давление в сосуде было Р1, то для этого момента можно так же применить закон Дальтона: Решаем полученные уравнение в системе относительно неизвестного: Дата добавления: 2018-04-04; просмотров: 3494; | |
Источник
