В закрытом сосуде в воде плавает пузырек
486. В чем различие передачи давления в случаях, показанных на рисунке 121?
В первом случае давление передается только на дно сосуда, а во втором — как на дно, так и на стенки сосуда.
487. Если выстрелить из мелкокалиберной винтовки в вареное яйцо, то в яйце образуется отверстие. Если же выстрелить в сырое яйцо, оно разлетится. Как объяснить это явление?
При выстреле в сырое яйцо давление, оказываемое пулей, передается по всем направлениям без изменения. Таким образом, скорлупа сырого яйца под действием этого давления разлетается.
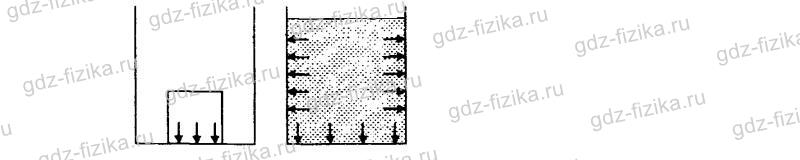
488. В одном сосуде находится металлический кубик, в другом — вода (рис. 122). Изобразите графически (одной—тремя стрелками), как эти тела будут передавать производимое на них давление.
489. Сосуд плотно закрыт пробкой, в которую вставлены две трубки (рис. 123). Если подуть в трубку а, то вода через трубку б выливается из сосуда. Будет ли вытекать вода из трубки а, если подуть в трубку б?
Если подуть в трубку б), то вода из трубки а) вытекать не будет.
490. Почему взрыв снаряда под водой губителен для живущих в воде организмов?
Потому что при взрыве снаряда развиваются большие давления, которые распространяются во все стороны (ударная волна).
491. Объясните действие фонтана, изображенного на рисунке 124.
При нагревании колбы давление воздуха в сосуде увеличивается и передается через трубку в пространство над жидкостью в правом сосуде. Как только это давление превысит атмосферное, вода начнет подниматься по трубке, и фонтан заработает.
492. Забавляясь, мальчик выдувает мыльные пузыри. Почему мыльные пузыри приобретают форму шара?
Потому что давление воздуха передается во все точки стенок мыльного пузыря одинаково.
493. В закрытом сосуде в воде плавает пузырек так, как показано на рисунке 125. Пузырек заполнен водой и воздухом. Будет ли увеличиваться масса воды в пузырьке, если увеличить давление воздуха в сосуде? Почему?
Если в сосуд накачать воздух, то давление увеличится в любой точке сосуда (в том числе и под водой). Поэтому уровень воды в пузырьке увеличится.
494. Поршень неподвижно прикреплен ко дну сосуда (рис. 126). Что произойдет с цилиндром, надетым на поршень, если в сосуд накачать воздух; откачать воздух из сосуда? Ответ поясните.
Если в сосуд накачать воздух, то цилиндр опустится. Если же воздух откачать, то цилиндр поднимется. Объясняется это тем, что при изменении в сосуде давления цилиндр изменяет свое положение (поднимается или опускается) таким образом, чтобы давления внутри и снаружи цилиндра были равны (рис. 126).
495. Будет ли, как и при обычном пользовании, выдавливаться зубная паста из тюбика в условиях состояния невесомости? Ответ поясните.
В состоянии невесомости зубная паста будет выдавливаться даже легче, чем обычно, потому что в земных условиях приходится преодолевать силу тяжести выдавливаемой пасты (если держать тюбик вертикально вверх).
496. Два сообщающихся сосуда с различными поперечными сечениями (рис. 127) наполнены водой. Площадь поперечного сечения у узкого сосуда в 100 раз меньше, чем у широкого. На поршень А поставили гирю весом 10 Н. Какой груз надо положить на поршень В, чтобы оба груза находились в равновесии?
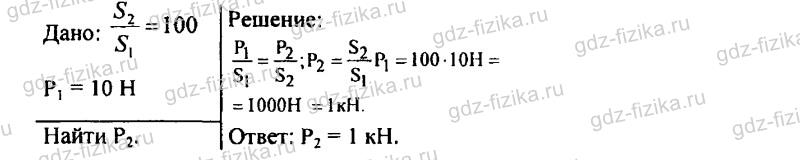
497. Какой выигрыш в силе можно получить на гидравлических машинах, у которых площади поперечных сечений поршней относятся как: а) 1:10; б) 2:50; в) 1:100; г) 5:60; д) 10:100?
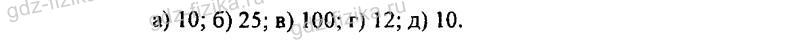
498. Площадь меньшего поршня гидравлического пресса 10 см2. На него действует сила 200 Н. Площадь большего поршня 200 см2. Какая сила действует на больший поршень?
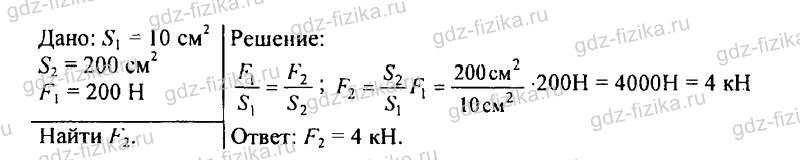
499. Поршень гидравлического пресса площадью 180 см2 действует силой 18 кН. Площадь малого поршня 4 см2. С какой силой действует меньший поршень на масло в прессе?
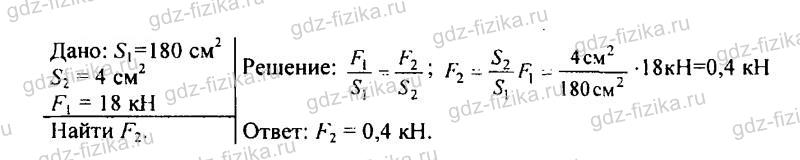
500. Определите (устно): а) каков вес шара (рис. 128), если жидкость в гидравлической машине находится в равновесии; б) какие силы действуют на тела, прессуемые гидравлическими машинами (рис. 129, а, б).

501. Малый поршень гидравлического пресса под действием силы 500 Н опустился на 15 см. При этом большой поршень поднялся на 5 см. Какая сила действует на большой поршень?

502. Малый поршень гидравлического пресса площадью 2 см2 под действием силы опустился на 16 см. Площадь большого поршня 8 см2. Определите: а) вес груза, поднятого поршнем, если на малый поршень действовала сила 200 Н; б) на какую высоту поднят груз.

503. Давление в гидравлической машине 400 кПа (рис. 130). На меньший поршень действует сила 200 Н. Площадь большого поршня 400 см2. Определите: а) показания динамометра В, сжимаемого большим поршнем; б) площадь меньшего поршня.
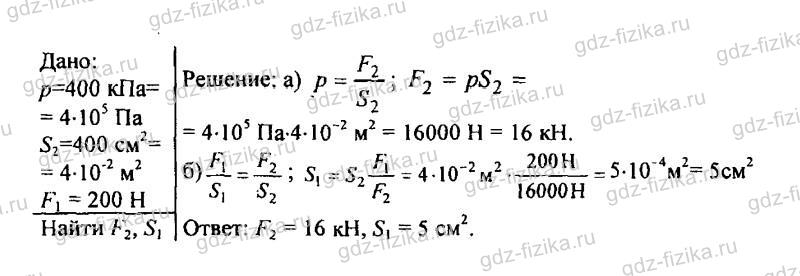
Источник
Сборник задач по физике, Лукашик В.И.
486. В чем различие передачи давления в случаях, показанных на рисунке 121?
В первом случае давление передается только на дно сосуда, а во втором — как на дно, так и на стенки сосуда.
487. Если выстрелить из мелкокалиберной винтовки в вареное яйцо, то в яйце образуется отверстие. Если же выстрелить в сырое яйцо, оно разлетится. Как объяснить это явление?
При выстреле в сырое яйцо давление, оказываемое пулей, передается по всем направлениям без изменения. Таким образом, скорлупа сырого яйца под действием этого давления разлетается.
488. В одном сосуде находится металлический кубик, в другом — вода (рис. 122). Изобразите графически (одной—тремя стрелками), как эти тела будут передавать производимое на них давление.
489. Сосуд плотно закрыт пробкой, в которую вставлены две трубки (рис. 123). Если подуть в трубку а, то вода через трубку б выливается из сосуда. Будет ли вытекать вода из трубки а, если подуть в трубку б?
Если подуть в трубку б), то вода из трубки а) вытекать не будет.
490. Почему взрыв снаряда под водой губителен для живущих в воде организмов?
Потому что при взрыве снаряда развиваются большие давления, которые распространяются во все стороны (ударная волна).
491. Объясните действие фонтана, изображенного на рисунке 124.
При нагревании колбы давление воздуха в сосуде увеличивается и передается через трубку в пространство над жидкостью в правом сосуде. Как только это давление превысит атмосферное, вода начнет подниматься по трубке, и фонтан заработает.
492. Забавляясь, мальчик выдувает мыльные пузыри. Почему мыльные пузыри приобретают форму шара?
Потому что давление воздуха передается во все точки стенок мыльного пузыря одинаково.
493. В закрытом сосуде в воде плавает пузырек так, как показано на рисунке 125. Пузырек заполнен водой и воздухом. Будет ли увеличиваться масса воды в пузырьке, если увеличить давление воздуха в сосуде? Почему?
Если в сосуд накачать воздух, то давление увеличится в любой точке сосуда (в том числе и под водой). Поэтому уровень воды в пузырьке увеличится.
494. Поршень неподвижно прикреплен ко дну сосуда (рис. 126). Что произойдет с цилиндром, надетым на поршень, если в сосуд накачать воздух; откачать воздух из сосуда? Ответ поясните.
Если в сосуд накачать воздух, то цилиндр опустится. Если же воздух откачать, то цилиндр поднимется. Объясняется это тем, что при изменении в сосуде давления цилиндр изменяет свое положение (поднимается или опускается) таким образом, чтобы давления внутри и снаружи цилиндра были равны (рис. 126).
495. Будет ли, как и при обычном пользовании, выдавливаться зубная паста из тюбика в условиях состояния невесомости? Ответ поясните.
В состоянии невесомости зубная паста будет выдавливаться даже легче, чем обычно, потому что в земных условиях приходится преодолевать силу тяжести выдавливаемой пасты (если держать тюбик вертикально вверх).
496. Два сообщающихся сосуда с различными поперечными сечениями (рис. 127) наполнены водой. Площадь поперечного сечения у узкого сосуда в 100 раз меньше, чем у широкого. На поршень А поставили гирю весом 10 Н. Какой груз надо положить на поршень В, чтобы оба груза находились в равновесии?
497. Какой выигрыш в силе можно получить на гидравлических машинах, у которых площади поперечных сечений поршней относятся как: а) 1:10; б) 2:50; в) 1:100; г) 5:60; д) 10:100?
498. Площадь меньшего поршня гидравлического пресса 10 см2. На него действует сила 200 Н. Площадь большего поршня 200 см2. Какая сила действует на больший поршень?
499. Поршень гидравлического пресса площадью 180 см2 действует силой 18 кН. Площадь малого поршня 4 см2. С какой силой действует меньший поршень на масло в прессе?
500. Определите (устно): а) каков вес шара (рис. 128), если жидкость в гидравлической машине находится в равновесии; б) какие силы действуют на тела, прессуемые гидравлическими машинами (рис. 129, а, б).
501. Малый поршень гидравлического пресса под действием силы 500 Н опустился на 15 см. При этом большой поршень поднялся на 5 см. Какая сила действует на большой поршень?
502. Малый поршень гидравлического пресса площадью 2 см2 под действием силы опустился на 16 см. Площадь большого поршня 8 см2. Определите: а) вес груза, поднятого поршнем, если на малый поршень действовала сила 200 Н; б) на какую высоту поднят груз.
503. Давление в гидравлической машине 400 кПа (рис. 130). На меньший поршень действует сила 200 Н. Площадь большого поршня 400 см2. Определите: а) показания динамометра В, сжимаемого большим поршнем; б) площадь меньшего поршня.
Источник
Задачи, тесты
Е. М.
Раводин,
, МОУ СОШ № 2, г. Прокопьевск, Кемеровская обл.
Окончание. См. № 5,
8/2010
18. Прямоугольная коробочка из жести массой m = 76 г с дном площадью S = 38 см2 и высотой H = 6 см плавает в воде. Определите высоту h надводной части коробочки.
Решение. Коробочка плавает, если действующая на неё сила тяжести равна по модулю действующей на неё силе Архимеда: mg = FА, причём FА = Vпчgρв, где  – объём погружённой части коробочки. Подставляя числовые данные, получаем
– объём погружённой части коробочки. Подставляя числовые данные, получаем 
Отсюда глубина погружения коробочки равна

Значит h = H – x = 4 см.
19. Льдина плавает на поверхности пресной воды. Какую часть составляет объём подводной части от объёма всей льдины? Если задача не решается в общем виде, то, для упрощения, примите объём льдины равным 100 м3. Плотность льда 900 кг/м3.
Решение. Раз льдина плавает, то её сила тяжести равна по модулю силе Архимеда: mg = FА, т. е.:

20. На поверхности широкого озера лёд имеет толщину 2 м. Какой минимальной длины надо взять верёвку, чтобы зачерпнуть кружкой воды из проруби?
Решение. Так как озеро широкое, то лёд на его поверхности может только плавать, а не держаться за берега за счёт примерзания к ним. Согласно решению задачи № 19, в проруби под поверхностью воды окажется 0,9 толщи льда, т. е. 0,9 · 2 м = 1,8 м, а над поверхностью воды 0,2 м = 20 см. Для зачерпывания воды с такой глубины верёвка не нужна.
21. В стакане с пресной водой плавает кусок льда. Изменится ли уровень воды, когда лёд растает? Рассмотрите дополнительно случаи: когда в лёд вмёрзла дробинка; когда в лёд вмёрз пузырёк воздуха.
Решение. Лёд плавает, если его вес равен весу жидкости в объёме погружённой части. Образовавшаяся изо льда пресная вода имеет тот же вес, что и лёд, и, следовательно, точно заполнит объём, который вытеснял плавающий лёд. Значит, уровень воды не изменится.
Если во льду была дробинка, лёд вытеснял больше воды, чтобы поддерживать на плаву дробинку. Когда лёд растаял, дробинка утонула (её вес больше веса вытесненной ею воды), уровень воды понизился.
В случае вмёрзшего пузырька уровень воды после таяния льдины практически не изменится. Хотя, если подсчитать точно, уровень воды несколько понизится, т. к. масса воздуха в пузырьке хоть и мала, но не равна нулю.
22. В прямоугольный сосуд с водой пустили плавать модель судна массой m = 4 кг. На сколько при этом повысился уровень воды, если площадь дна сосуда S = 2000 см2?
Решение. Вес сосуда при опускании в него модели увеличится на вес модели mg. Это увеличение веса можно интерпретировать как следствие подъёма уровня воды на ∆h и, следовательно, увеличения силы давления воды ∆Fд = ρвg∆hS. Отсюда:

23. Кусок парафина массой m = 200 г плавает на границе раздела воды и бензина. Определите объём V1 надводной части бруска. Плотность парафина 900 кг/м3, бензина 700 кг/м3.
Решение. Если парафин плавает, то сила тяжести равна сумме сил Архимеда в обеих жидкостях: mg = Vвρвg + V1ρб g, где Vв – объём, погружённый в воду, V1 – искомый надводный объём (в бензине). Общий объём парафина 
Решая совместно оба уравнения, получаем:

24. Кусок льда, внутрь которого вморожен шарик из свинца, плавает в цилиндрическом сосуде с водой. Площадь дна сосуда S. Какова масса шарика, если после полного таяния льда уровень воды в сосуде понизился на H? Плотность свинца ρ1, плотность воды ρ2.
Решение. На плавающую льдину со свинцовым шариком действует бóльшая сила Архимеда, чем на такую же льдину без шарика, т. к. она тяжелее на силу тяжести шарика mg. Следовательно, объём вытесняемой в первом случае воды больше, чем во втором, на  Но когда льдина растает, шарик упадёт на дно и займёт объём V1 = m/ρ1. Общее уменьшение объёма воды в конечном счёте ∆V = ∆Vп – V1. Так как ∆V = SH (по условию), то приходим к уравнению:
Но когда льдина растает, шарик упадёт на дно и займёт объём V1 = m/ρ1. Общее уменьшение объёма воды в конечном счёте ∆V = ∆Vп – V1. Так как ∆V = SH (по условию), то приходим к уравнению: 
25. Корона царя Гиерона в воздухе весит P1 = 20 Н, а в воде P2 = 18,75 Н. Вычислите плотность вещества короны. Была ли она из чистого золота? Дополнение: найдите, сколько золота и сколько серебра было в короне. Плотность золота округлённо принять 20 000 кг/м3, а серебра 10 000 кг/м3.
Решение. Для оценки добросовестности мастера найдём плотность короны по формуле  полученной при решении задачи 9 (см. № 5/2010):
полученной при решении задачи 9 (см. № 5/2010):

– корона не из чистого золота.
Чтобы найти состав короны, используем два факта: 1) общая масса короны m = mз + mс; 2) общий объём короны V = Vз + Vс (индексы «з» и «с» относятся к золоту и серебру соответственно). Заменяя объёмы их выражениями через массы и плотности, получаем систему из двух уравнений:

Решение
Опуская громоздкие промежуточные вычисления, запишем ответ:

26. Какую силу надо приложить к пробковому телу массой 400 кг, чтобы удерживать его, когда оно целиком погружено в воду? ρп = 200 кг/м3; g = 10 м/с2.
Решение. Сила тяжести тела mg = 4000 Н направлена вниз, сила Архимеда направлена вверх и равна

Чтобы удержать тело в воде, надо приложить направленную вниз силу F = FА – mg = 16 кН.
27. Чугунная плита толщиной 0,5 м, длиной 10 м и шириной 4 м лежит на глинистом дне, выдавив из-под себя воду. Глубина водоёма 2,5 м. Какую силу необходимо приложить, чтобы начать подъём плиты?
Решение. Объём плиты V = 0,5 м · 10 м · 4 м = 20 м3.
Её масса m = Vρч = 20 м3 · 7000 кг/м3 = 140 000 кг.
Сила тяжести mg = 1 400 000 Н.
Поскольку под плитой нет воды, сила Архимеда на неё не действует. Вниз на плиту, кроме силы тяжести, действуют сила давления воды на глубине 2,5 – 0,5 = 2 (м) и сила давления атмосферы, которую передаёт вода по закону Паскаля. При нормальном атмосферном давлении общее давление на плиту:
p = pв + pа = 1,2 · 105 Па.
Горизонтальная площадь поверхности плиты
S = 40 м2. Сила давления на плиту F = pS = 4,8 · 106 Н.
Полная сила, прижимающая плиту к грунту:
F = mg + Fа = 1,4 · 106 Н + 4,8 · 106 Н = 6,2 ·106 Н.
Для отрыва от грунта нужна сила F > 6,2 МН.
Источник
Коткин Г. Всплывающий воздушный пузырек и закон Архимеда // Квант. – 1976. – № 1. – С. 19-23. (1996. – № 3. – С. 50-51.)
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Представьте себе, что вы готовитесь к экзамену по физике, расположившись на лесной опушке на берегу озера. Повторяя второй закон Ньютона, бы хотите применить этот закон к движению всплывающих со дна пузырьков газа. И тут начинается что-то странное…
Сила тяжести, действующая на пузырек, раз в тысячу меньше веса вытесняемой им воды (плотности воздуха и воды отличаются примерно в тысячу раз). Сила сопротивления при жидком трении, пропорциональная скорости пузырька, поначалу мала, поэтому ее учитывать не стоит (О роли силы сопротивления будет сказано дальше.). Таким образом, ускорение определяется, в основном, архимедовой выталкивающей силой:
(1)
Здесь m – масса, а – ускорение пузырька, V – его объем, ρ – плотность воды. Пусть плотность газа ρ0. Тогда
Итак, ускорение пузырька порядка тысячи g. Это очень большая величина. Вспомним, что ускорение, которое приходится переносить космонавтам к летчикам, достигает нескольких g (скажем, до 10g). Если снаряд будет двигаться в стволе длиной 1 м с таким ускорением, то он сможет взлететь на высоту h = 1 км (проверьте это самостоятельно); если внутрь нашего всплывающего пузырька попадет букашка, она будет раздавлена в таком «лифте»; и т.д. и т.п. Поистине богатые возможности для изобретателей.
Впрочем, сидя на берегу озера, можно увидеть собственными глазами, что на самом деле ускорение пузырька вовсе не так велико.
Вместо того чтобы сразу дать ответ на возникшую загадку, зададим еще одну.
Пусть вы без труда можете поднять пудовую гирю (m = 16 кг) на высоту 1 м. А что если приложить силу, равную весу этой гири, к камешку массы 1 г (или к копеечной монете) на пути тоже в 1 м? Нетрудно сообразить, что камешек после этого взлетит на высоту 16 км. (Сопротивление воздуха не учитываем. Ясно, что дело не в нем.) Что это – еще один фантастический проект? Нет, на этот раз разоблачить автора проекта совсем легко: поднимать придется не только камешек, но и собственную руку! К каждому ее грамму нужно приложить силу порядка 160 Н. Вся рука будет весить несколько тонн, и поднять ее не хватит сил.
Таким образом, неподвижная или движущаяся с небольшим ускорением рука может приложить к грузу силу гораздо большую, чем рука, которая движется с большим ускорением.
Но ведь при движении воздушного пузырька в воде возникает аналогичная картина. Когда пузырек поднимается, некоторая масса воды устремляется вниз, заполняя освобожденное место. Пузырек взаимодействует с движущейся, а не с неподвижной водой. По-видимому, и сила, действующая со стороны воды на пузырек, зависит от ускорения самой воды. Закон Архимеда, записанный в обычном виде , неприменим к пузырьку, движущемуся ускоренно!
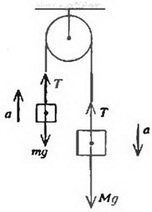
Рис. 1.
Оказывается, задача о пузырьке очень близка к задаче о движении грузиков, связанных переброшенной через неподвижный блок нитью (рис. 1). Нетрудно увидеть аналогию между ними. Действительно, один из грузиков (с массой m) как бы играет роль пузырька, другой (с массой М) – роль воды, а натяжение нити Т – роль выталкивающей силы.
Второй закон Ньютона в применении к грузику массы m можно записать так:
(2)
Если грузик массы m удерживать, то натяжение нити Т окажется численно равным весу грузина Mg (весу «вытесненной» воды). Подставив в уравнение (2), получаем:
(неверно!). (3)
При оказывается . Этот вывод своей нелепостью похож на вывод об огромном ускорении пузырька (см. (1)). Причина обеих ошибок одна и та же: необходимо учитывать движение грузика массы М и движение «вытесненной» воды. Напомним, что для правильного решения задачи о грузиках нужно записать еще уравнение второго закона Ньютона для грузика массы М
(4)
и решить систему уравнений (2) и (4). Отсюда
(5)
При оказывается , что вполне соответствует действительности.
Можно решить эту задачу и другим способом – воспользоваться законом сохранения энергии. При смещении грузика массы m вверх (и соответственно, грузика массы М вниз) на расстояние h потенциальная энергия системы уменьшится на величину . Кинетическая энергия станет равной , где υ – скорость грузиков (начальную скорость считаем равной нулю). Приравняв величины
находим
или (см. (5))
(6)
Такая связь скорости и перемещения характерна для движения с постоянным ускорением а. (В данном случае )
Воспользуемся этим для решения задачи о движении тела в жидкости. Правда, привести полное решение задачи о воздушном пузырьке мы не сможем. Дело в том, что распределение скоростей жидкости вокруг пузырька слишком сложно (рис. 2).
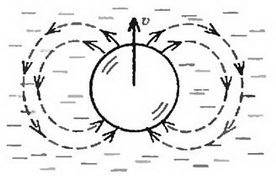
Рис. 2.
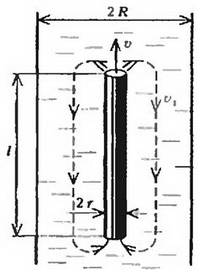
Однако мы решим похожую задачу. Рассмотрим движение длинного стержня радиуса r, длины l и массы m вдоль оси заполненной жидкостью плотности с трубки радиуса (рис. 3).

Рис 3.
В этом случае движение жидкости легко рассчитать. Вытесняемая верхней частью стержня жидкость смещается вниз и заполняет место, освобождаемое нижней частью стержня. Если исключить небольшие участки вблизи торцов стержняt то скорость жидкости всюду между стержнем и стенками трубки оказывается одной и той же. Обозначим через υ скорость стержня, а через υ1 —скорость воды, движущейся между стержнем и стенками трубки, в тот момент, когда стержень поднялся на высоту h от того уровня, на котором его скорость была равна нулю. Приравняв объем жидкости, вытесненной стержнем за малый промежуток времени Δt, объему жидкости, прошедшей за это же время между стержнем и трубкой, находим
За то время, пока стержень поднимался на высоту h, масса жидкости, равная ( – объем стержня), опустится тоже на h, тогда уменьшение потенциальной энергии стержня и жидкости равно . Кинетическая энергия системы равна , где m1 – масса движущейся жидкости. Кинетическую энергию жидкости удобно записать в таком виде:
где
Воспользовавшись законом сохранения энергии, получим
откуда
Такой зависимости скорости υ от перемещения h отвечает движение с ускорением (см. (6))
(7)
Таким образом, стержень движется так, будто бы его масса увеличилась на величину m‘, а выталкивающая сила осталась равной гидростатической архимедовой силе . Величину m‘ называют присоединенной массой. Это чисто формальное, но удобное толкование равенства (7). Формула (7) получается из неправильной формулы (1) добавлением в знаменателе слагаемого m‘. Отметим, что подобным же образом формула (5) получается из (3) добавлением в знаменателе слагаемого М.
Силу Fвыт, с которой движущаяся жидкость действует на стержень, теперь легко получить из второго закона Ньютона
откуда
(8)
В частности, если , то ; при выталкивающая сила оказывается порядка веса стержня (и не имеет отношения к весу вытесненной воды). Если же то то есть мы возвращаемся к закону Архимеда в обычном виде.
< style=”text-transform: uppercase”>Для шарика (в частности, для пузырька) расчет дает такой результат: кинетическая энергия жидкости равна где V – объем шарика, υ – его скорость. Тогда присоединенная масса для пузырька т.е. она равна половине массы вытесненной воды. Пузырек всплывает с ускорением
Выталкивающая сила определяется из уравнения (8), она приблизительно равна т.е. тройному весу неподвижного пузырька (и во много раз меньше веса вытесненной воды).
Теперь вспомним о силе сопротивления, Для пузырька газа в жидкости она определяется формулой где r – радиус пузырька, υ – его скорость, η – так называемый коэффициент вязкости среды (Приведенная формула справедлива при если , коэффициент 12πследует заменить на 4π. Дли твердого шарика при коэффициент равен 6π (формула Стокса).). С учетом силы сопротивления уравнение движения пузырька запишется так (см. (7)):
(9)
Очевидно, что Fс уменьшает ускорение (а значит, и скорость) пузырька по сравнению с тем случаем, когда мы не учитываем сопротивление жидкости. Однако, если т.е. при силой сопротивления можно пренебречь. Например, если речь идет о пузырьке радиуса r = 3 мм (Пузырек большего радиуса не может сохранить шарообразную форму (подобно падающей дождевой капле, деформируемой силой давления воздуха; см., например, статью И.Ш. Слободецкого «О форме дождевой капли», «Квант», 1970, № 8).), движущемся в воде (ρ = 1 г/см3, η = 1,0•10–2 г/(см•с), то его скорость должна быть много меньше величины Прикинем, на каком пути h0, пузырек достигнет такой скорости. Для грубой опенки воспользуемся равенством где
Таким образам, на пути 1,5 м силой сопротивления можно пренебречь. При этом υ0 = 10 м/с – это предельная скорость, которой может достичь всплывающий пузырек газа в воде.
Упражнения
1. Цилиндрическая труба, состоящая из двух частей с радиусами R1 и R2 (рис. 4), соединенных плавным переходом, заполнена водой. Вдоль осп трубы движется длинный стержень радиуса r и плотности ρ0. Скорость стержня а левой части трубы равна υ1. Какой станет его скорость после перехода в правую часть трубы?
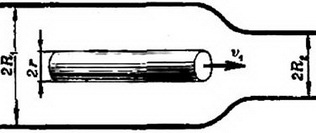
Рис. 4.
2. В жидкости плотности ρ плавает шарик радиуса R с трубкой радиуса . (рис. 5). Масса шарика с трубкой ранка m. Шарик удален от поверхности жидкости, дна и стенок сосуда на расстояние, много большее его радиуса. Шарик слегка приподняли за трубку и отпустили. Определить период возникших колебаний шарика.

Рис. 5.
3. Вдоль оси трубки с водой всплывает стержень массы m (рис. 6). Определить силу, действующую на дно.
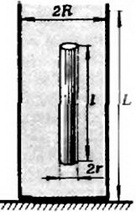
Рис. 6.
Ответы
1. Из закона сохранения энергии где (V – объем стержня), (ρ —плотность поды), находим
2. (Решение задачи см., например, в «Кванте», 1974, № 6, с. 36. Только нужно m заменить на
3. Запишем второй закон Ньютона для стержня, для массы воды, движущейся между стержнем и стенками трубки, и для остальной, неподвижной воды массы
Здесь Fвыт1 (Fвыт2) – сила, с которой движущаяся (неподвижная) вода действует на стержень, F1 – сила взаимодействия < style=”text-transform: uppercase”>подвижной и неподвижной воды, F – сила, с которой на неподвижную воду действует дно трубки. Сложив все три уравнения, исключаем силы Fвыт1, Fвыт2 и F1. Заметим, что Тогда после несложных преобразовании получаем:
Отсюда видно, что сила давления воды на дно (численно равная силе F) меньше суммарного веса волы и стержня. Причем это справедливо и когда стержень всплывает , и когда он тонет .
Источник
