В замкнутом сосуде протекает реакция константа равновесия
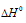
Задача 356.
Для реакции Н2(г) + Br2(г) = 2HBr(г) при некоторой температуре К = 1. Определить состав (в процентах по объему) равновесной реакционной смеси, если исходная смесь состояла из 3 молей Н2 и 2 молей Вг2.
Решение:
Уравнение реакции имеет вид:
Н2(г) + Br2(г) = 2HBr(г)
Согласно уравнению реакции из 1 моля Н2 и 1 Br2 образуется 2 моль HBr. Обозначим количество израсходованных исходных веществ через x. Тогда равновесные концентрации реагирующих веществ будут раны:
[Н2] = (3 – х) моль/л, [Br2] = (2 – х) моль/л, [HBr] = (2х) моль/л. Подставив эти значения концентраций в выражение константы равновесия реакции, рассчитаем значение x:
Тогда равновесные концентрации веществ будут равны:
[Н2] = 3 – 0,808 = 2,192 моль/л;
[Br2] = 2 – 0,808 = 1,192 моль/л;
[HBr] = 2 . 0,808 = 1,616 моль/л.
Находим объёмы газов в равновесной системе, учитывая, что 1 моль любого газа при нормальных условиях занимает 22,4л, получим:
Тогда общий объём газовой равновесной системы будет равен 112 л (49,1 + 26,7 + 36,2 = 112).
Теперь определим состав газов (в процентах по объему) равновесной реакционной смеси по формуле:
w% – объёмная доля вещества, выраженная в процентах, V(в-ва) – объём вещества, V(смеси) – общий объём газовой смеси.
Тогда
Ответ: 43,84% Н2; 23,84% Br2; 32,32%HBr.
Задача 357.
Константа равновесия реакции равна единице. Сколько процентов вещества А подвергнется превращению, если смешать З моля вещества А и 5 молей вещества В?
Решение:
Уравнение реакции имеет вид:
А(г) + В(г) = С(г) + D(г)
Согласно уравнению реакции из 1 моля вещества А и 1 моля вещества В образуется по 1 молю веществ С и D. Обозначим равновесные концентрации веществ С и D через x. Тогда равновесные концентрации веществ будут раны: [C] = [D] = моль/л, [A] = (3 – х)моль/л, [B] = (5 – х)моль/л. Подставив эти значения концентраций в выражение кон-станты равновесия реакции, рассчитаем значение x:
Теперь рассчитаем, сколько процентов вещества А подвергнется превращению из пропорции:
3 : 100 = 1,875 : x; x = (1,875 . 100)/3 = 62,5%
Ответ: 62,5%.
Задача 358.
После смешивания газов А и В в системе А(г) + В(г) = С(г) + D(г) устанавливается равновесие при следующих концентрациях: [B] = 0,05 моль/л; [C] = 0,02 моль/л. Константа равновесия реакции равна 4.102. Найти исходные концентрации веществ А и В.
Решение:
Уравнение реакции имеет вид:
А(г) + В(г) = С(г) + D(г) .
Согласно уравнению реакции из 1 моля вещества А и 1 моля вещества В образуется по 1 молю веществ С и D.
Поскольку по условию задачи в каждом литре системы образовалось 0,02 моля вещества С, то такое же количество образовалось вещества D, было израсходовано по 0,02 моля веществ А и В.
Сначала найдём концентрацию вещества А из выражения для константы равновесия реакции:
Отсюда рассчитаем искомые исходные концентрации веществ А и В:
[A]0 = 0,2 + 0,02 = 0,22 моль/л;
[B]0 = 0,05 + 0.02 = 0,07 моль/л.
Ответ: [A]0 = 0,22 моль/л; [B]0 = 0,07 моль/л.
Задача 359.
Найти константу равновесия реакции N2O4 ⇔ 2NO2, если начальная концентрация N2O4 составляла 0,08 моль/л, а к моменту наступления равновесия диссоциировало 50% N2O4.
Решение:
Уравнение реакции имеет вид: N2O4 ⇔ 2NO2. Из уравнения реакции следует, что из 1 моля N2O4 образуется 2 моля NO2. Поскольку по условию задачи 50% N2O4 диссоциировало, то количество N2O4, продиссоциировавшегося составляет 0,04 моль/л (0,08 . 0,5 = 0,04).
Тогда равновесные концентрации участвующих веществ будут равны:
[N2O4]0 = 0,08 – 0,04 = 0,04 моль/л;
[NO2]0 = 0,04 .2 = 0,08 моль/л
Выражение для константы равновесия для данной реакции будет иметь вид:
Подставляя в это выражение данные из задачи, получим:
Ответ: 0,16
Задача 360.
В замкнутом сосуде протекает реакция АВ(г) ⇔ А(г) + В(г) Константа равновесия реакции равна 0,04, а равновесная концентрация вещества В составляет 0,02 моль/л. Найти начальную концентрацию вещества АВ. Сколько процентов вещества АВ разложилось?
Решение:
Уравнение реакции имеет вид: АВ(г) ⇔ А(г) + В(г). Из уравнения реакции следует, что из 1 моля вещества АВ образуется 1 моль вещества А и 1 моль вещества В. Поскольку по условию задачи в каждом литре системы образовалось 0,02 моля вещества В, то столько же образовалось и вещества А, при этом было израсходовано 0,02 моля вещества АВ.
Константа равновесия данной реакции выражается уравнением
Подставляя в это выражение данные задачи, рассчитаем равновесную концентрацию вещества АВ:
Таким образом, искомая исходная концентрация вещества АВ будет равна:
[AB]0 = 0,02 + 0,01 = 0,03 моль/л
Сколько процентов вещества АВ разложилось находим из пропорции:
0,03 : 100 = 0,02 : х = (0,02 . 100)/0,03 = 66,7%
Ответ: [AB]0 = 0,03 моль/л; 66,67%.
Источник
Задача 350.
Реакция СО + С12 ⇔ СОС12 протекает в закрытом сосуде при постоянной температуре; исходные вещества взяты в эквивалентных количествах. К моменту наступления равновесия остается 50% начального количества СО. Определить давление равновесной газовой смеси, если первоначальное давление равнялось 100 кПа (750 мм рт. ст.).
Решение:
Уравнение реакции имеет вид:
СО + С12 ⇔ СОС12
По условию задачи в реакцию вступило 50% СО. Из уравнения реакции следует, что из 1 моля СО и 1 моля С12 образуется 1 моль СОС12. Следовательно, из 0,5 моль СО и 0,5 моль С12 образовалось тоже 0,5 молей СОС12. Учитывая, что вещества реагируют друг с другом в эквивалентных количествах, значит, в 1л реакционной смеси содержится 2 моля исходных веществ (СО и С12), половина из которых прореагировало с образованием 0,5 молей СОС12.
Таким образом, количество системы уменьшилось на 0,5 молей и составило после протекания реакции 1,5 молей (2 – 0,5 = 1,5). Следовательно, давление равновесной газовой смеси определится из пропорции:
2 : 1,5 = 100 : х; х = (1,5 . 100)/2 = 75 кПа.
Ответ: 75кПа.
Задача 351.
В закрытом сосуде установилось равновесие: СО2(г.) + Н2(г.) ⇔ СО(г.) + +Н2О(г.); константа равновесия равна единице. Определить: а) сколько процентов СО2 подвергнется превращению в СО при данной температуре, если смешать 1 моль СО2 и 5 молей Н2? б) в каких объемных соотношениях были смешаны СО2 и Н2, если к моменту наступления равновесия в реакцию вступило 90% первоначального количества водорода?
Решение:
а) Уравнение реакции имеет вид
СО2(г.) + Н2(г.) ⇔ СО(г.) + +Н2О(г.)
Из уравнения следует, что из 1 моля СО2 и 1 моля Н2 образуется по 1 молю СО и Н2О.
Обозначим равновесную концентрацию СО и Н2О через х, тогда [CO] = [H2O]. Таким образом, равновесные концентрации СО2 и Н2 будут составлять, соответственно, (1 – х) и (5 – х)моль/л, а СО и Н2О – по х моль/л. Подставим эти значения в выражение константы равновесия реакции:
Таким образом, 83,3% СО2 подвергнется разложению в СО, учитывая, что [CO2] = 1 моль/л.
б) Находим количество Н2, которое вступило в реакцию: 5 . 0,9 = 4,5 моль/л. Остаток количества СО2 и Н2 одинаков и будет составлять 0,5 моль/л (5 – 4,5 = 0,5). Тогда объёмные соотношения СО2 и Н2, к моменту наступления равновесия, составляют:
V(H2) : V(CO2) = 4,5 : 0,5 = 9 : 1 .
Ответ: а) 83,3%; б) 9:1.
Задача 352.
При состоянии равновесия в системе:
N2(г) + 3H2(г) ⇔ 2NН3(г); = -92,4 кДж
концентрации участвующих веществ равны: [N2] = 3 моль/л; [H2] = 9 моль/л; [NН3] = 4 моль/л. Определить: а) исходные концентрации Н2 и N2 б) в каком направлении сместится равновесие с ростом температуры? в) в каком направлении сместится равновесие, если уменьшить объем реакционного сосуда?
Решение:
а) Для нахождения исходных концентраций веществ N2 и Н2 учтём, что, согласно уравнению реакции из 1 моля N2 и 3 молей Н2 образуется 2 моля NH3. Поскольку по условию задачи в каждом литре системы образовалось 4 моля NH3, то при этом было израсходовано 1/2 . 4 = 2 моля N2 и 3/4 . 4 = 6 молей Н2. Таким образом, искомые исходные концентрации N2 и Н2 равны:
[N2]0 = 3 + 2 = 5 моль/л;
[H2]0 = 6 + 3 = 9 моль/л.
б) Из уравнения реакции следует, что данная реакция экзотермическая, т.е. протекает с выделением теплоты. Поэтому при повышении температуры в экзотермической системе, согласно принципу Ле Шателье, равновесие системы сместится в сторону уменьшения действия температуры, т.е. влево.
в) Реакция протекает с уменьшением числа молей газообразных веществ, т.е. с уменьшением объёма и, соответственно, с уменьшением давления в системе. Поэтому при уменьшении объёма реакционного сосуда равновесие системы сместится в сторону образования аммиака, вправо, т.е. согласно принципу Ле Шателье, в сторону уменьшения действия (повышения давления при уменьшении объёма реакционного сосуда).
Ответ: а) [N2]0 = 5 моль/л, [H2]0 = 6 + 3 = 9 моль/л; б) влево; в) вправо.
Задача 353.
Константа равновесия реакции FeO(к) + CO(г) ⇔ Fe(к) + CO2(г), при некоторой температуре равна 0,5. Найти равновесные концентрации СО и СО2, если начальные концентрации этих веществ составляли: [СО] = 0,05 моль/л, [СО2] = 0,01 моль/л.
Решение:
Для нахождения равновесных концентраций веществ учтем, что, согласно уравнению реакции из 1 моля СО образуется 1 моль СО2. Обозначим количество, прореагировавшего вещества СО за x моль. Учитывая, что моль СО2 образуется при реакции, то при этом равновесная концентрация СО будет равна (0,05 – х)моль/л, а СО2 – (0,01 + х) моль/л.
Таким образом, подставив в выражение константы равновесия реакции эти концентрации, найдём значение:
Отсюда искомые равновесные концентрации веществ равны:
[СО]равн. = 0,05 – 0,01 = 0,04 моль/л;
[СО2]равн. = 0,01 + 0,01 = 0,02 моль/л.
Ответ: [СО] = 04 моль/л; [СО2] = 0,02 моль/л.
Задача 354.
Равновесие в системе H2(г) + I2(г) ⇔ 2HI(г) установилось пи следующих концентрациях: [H2] = 0,025 моль/л; [I2] = 0,005 моль/л; [HI] = 0,09 моль/л. Определить исходные концентрации йода и водорода.
Решение:
Для нахождения исходных концентраций йода и водорода учтём, что согласно уравнению реакции, из 1 моля йода и 1 моля водорода образуется 2 моля йодоводорода. Поскольку по условию задачи в каждом литре системы образовалось 0,09 молей вещества HI, то при этом было затрачено 0,045 (0,09/2 = 0,045) молей H2 и, соответственно 0,045 молей I2.
Отсюда находим исходные концентрации водорода и йода:
[I2]исх. = 0,005 + 0,045 = 0.0 5моль/л;
[H2]исх. =.0,025 + 0,045 = 0,07 моль/л.
Ответ: [H2]исх. = 0,07 моль/л; [I2]исх. = 0.05 моль/л.
Задача 355.
При некоторой температуре равновесие в системе 2NO2 ⇔ 2NO + O2 установилось при следующих концентрациях: [NO2] = 0,006 моль/л; [NO] = 0,024 моль/л. Найти константу равновесия реакции и исходную концентрацию NO2.
Решение:
Константа равновесия данной реакции выражается уравнением:
Учитывая, что равновесная концентрация О2 будет составлять 1/2 концентрации NO, т.е. 0,012 моль/л (0,024/2 = 0,012), рассчитаем константу равновесия:
Для нахождения исходной концентрации NO2 учтём, что согласно уравнению реакции из 1 моля NO2 образуется 1 моль NO. Поскольку по условию задачи в каждом литре системы образовалось 0,024 моля NO, то при этом было израсходовано 0,024 моля NO2.
Таким образом, искомая исходная концентрация NO равна:
[NO2]исх. = 0,006 + 0,024 = 0,03 моль/л.
Ответ: К = 0,192; [NO2]исх. = 0,03 моль/л.
Источник
Ó÷åáíûå ìàòåðèàëû ïî ôèçè÷åñêîé õèìèè
Çàäà÷è ïî ôèçè÷åñêîé õèìèè.×àñòü 1.Õèìè÷åñêàÿ òåðìîäèíàìèêà
9. Õèìè÷åñêîå ðàâíîâåñèå
Õèìè÷åñêèì ðàâíîâåñèåì íàçûâàåòñÿ òàêîå ñîñòîÿíèå îáðàòèìîé õèìè÷åñêîé ðåàêöèè
aA + bB = cC + dD,
ïðè êîòîðîì ñ òå÷åíèåì âðåìåíè íå ïðîèñõîäèò èçìåíåíèÿ êîíöåíòðàöèé ðåàãèðóþùèõ âåùåñòâ â ðåàêöèîííîé ñìåñè. Ñîñòîÿíèå õèìè÷åñêîãî ðàâíîâåñèÿ õàðàêòåðèçóåòñÿ êîíñòàíòîé õèìè÷åñêîãî ðàâíîâåñèÿ:
, (9.1)
ãäå Ci – êîíöåíòðàöèè êîìïîíåíòîâ â ðàâíîâåñíîé èäåàëüíîé ñìåñè.
Êîíñòàíòà ðàâíîâåñèÿ ìîæåò áûòü âûðàæåíà òàêæå ÷åðåç ðàâíîâåñíûå ìîëüíûå äîëè Xi êîìïîíåíòîâ:
. (9.2)
Äëÿ ðåàêöèé, ïðîòåêàþùèõ â ãàçîâîé ôàçå, êîíñòàíòó ðàâíîâåñèÿ óäîáíî âûðàæàòü ÷åðåç ðàâíîâåñíûå ïàðöèàëüíûå äàâëåíèÿ Pi êîìïîíåíòîâ:
. (9.3)
Äëÿ èäåàëüíûõ ãàçîâ Pi = CiRT è Pi = XiP, ãäå P – îáùåå äàâëåíèå, ïîýòîìó KP, KC è KX ñâÿçàíû ñëåäóþùèì ñîîòíîøåíèåì:
KP = KC (RT) c+d-a-b = KXP c+d-a-b. (9.4)
Êîíñòàíòà ðàâíîâåñèÿ ñâÿçàíà ñ rGo õèìè÷åñêîé ðåàêöèè:
(9.5)
(9.6)
Èçìåíåíèå rG èëè rF â õèìè÷åñêîé ðåàêöèè ïðè çàäàííûõ (íå îáÿçàòåëüíî ðàâíîâåñíûõ) ïàðöèàëüíûõ äàâëåíèÿõ Pi èëè êîíöåíòðàöèÿõ Ci êîìïîíåíòîâ ìîæíî ðàññ÷èòàòü ïî óðàâíåíèþ èçîòåðìû õèìè÷åñêîé ðåàêöèè (èçîòåðìû Âàíò-Ãîôôà):
. (9.7)
. (9.8)
Ñîãëàñíî ïðèíöèïó Ëå Øàòåëüå, åñëè íà ñèñòåìó, íàõîäÿùóþñÿ â ðàâíîâåñèè, îêàçàòü âíåøíåå âîçäåéñòâèå, òî ðàâíîâåñèå ñìåñòèòñÿ òàê, ÷òîáû óìåíüøèòü ýôôåêò âíåøíåãî âîçäåéñòâèÿ. Òàê, ïîâûøåíèå äàâëåíèÿ ñäâèãàåò ðàâíîâåñèå â ñòîðîíó óìåíüøåíèÿ êîëè÷åñòâà ìîëåêóë ãàçà. Äîáàâëåíèå â ðàâíîâåñíóþ ñìåñü êàêîãî-ëèáî êîìïîíåíòà ðåàêöèè ñäâèãàåò ðàâíîâåñèå â ñòîðîíó óìåíüøåíèÿ êîëè÷åñòâà ýòîãî êîìïîíåíòà. Ïîâûøåíèå (èëè ïîíèæåíèå) òåìïåðàòóðû ñäâèãàåò ðàâíîâåñèå â ñòîðîíó ðåàêöèè, ïðîòåêàþùåé ñ ïîãëîùåíèåì (âûäåëåíèåì) òåïëîòû.
Êîëè÷åñòâåííî çàâèñèìîñòü êîíñòàíòû ðàâíîâåñèÿ îò òåìïåðàòóðû îïèñûâàåòñÿ óðàâíåíèåì èçîáàðû õèìè÷åñêîé ðåàêöèè (èçîáàðû Âàíò-Ãîôôà)
(9.9)
è èçîõîðû õèìè÷åñêîé ðåàêöèè (èçîõîðû Âàíò-Ãîôôà)
. (9.10)
Èíòåãðèðîâàíèå óðàâíåíèÿ (9.9) â ïðåäïîëîæåíèè, ÷òî rH ðåàêöèè íå çàâèñèò îò òåìïåðàòóðû (÷òî ñïðàâåäëèâî â óçêèõ èíòåðâàëàõ òåìïåðàòóð), äàåò:
(9.11)
(9.12)
ãäå C – êîíñòàíòà èíòåãðèðîâàíèÿ. Òàêèì îáðàçîì, çàâèñèìîñòü ln KP îò 1/Ò äîëæíà áûòü ëèíåéíîé, à íàêëîí ïðÿìîé ðàâåí -rH/R.
Èíòåãðèðîâàíèå â ïðåäåëàõ K1, K2, è T1,T2 äàåò:
(9.13)
(9.14)
Ïî ýòîìó óðàâíåíèþ, çíàÿ êîíñòàíòû ðàâíîâåñèÿ ïðè äâóõ ðàçíûõ òåìïåðàòóðàõ, ìîæíî ðàññ÷èòàòü rH ðåàêöèè. Ñîîòâåòñòâåííî, çíàÿ rH ðåàêöèè è êîíñòàíòó ðàâíîâåñèÿ ïðè îäíîé òåìïåðàòóðå, ìîæíî ðàññ÷èòàòü êîíñòàíòó ðàâíîâåñèÿ ïðè äðóãîé òåìïåðàòóðå.
ÏÐÈÌÅÐÛ
Ïðèìåð 9-1. Ðàññ÷èòàòü êîíñòàíòó ðàâíîâåñèÿ äëÿ ðåàêöèè
CO(ã) + 2H2(ã) = CH3OH(ã)
ïðè 500 K. fGoäëÿ CO(ã) è CH3OH(ã) ïðè 500 Ê ðàâíû -155.41 êÄæ. ìîëü-1 è -134.20 êÄæ. ìîëü-1 ñîîòâåòñòâåííî.
Ðåøåíèå. Goðåàêöèè:
rGo= fGo(CH3OH) – fGo(CO) = -134.20 – (-155.41) = 21.21 êÄæ. ìîëü-1.
= 6.09 10-3.
Ïðèìåð 9-2. Êîíñòàíòà ðàâíîâåñèÿ ðåàêöèè
N2(ã) + 3H2(ã) = 2NH3(ã)
ðàâíà KP = 1.64 10-4 ïðè 400o C. Êàêîå îáùåå äàâëåíèå íåîáõîäèìî ïðèëîæèòü ê ýêâèìîëÿðíîé ñìåñè N2 è H2, ÷òîáû 10% N2 ïðåâðàòèëîñü â NH3? Ãàçû ñ÷èòàòü èäåàëüíûìè.
Ðåøåíèå. Ïóñòü ïðîðåàãèðîâàëî ìîëü N2. Òîãäà
Ñëåäîâàòåëüíî, KX = è KP = KX.P-2 = .
Ïîäñòàâëÿÿ = 0.1 â ïîëó÷åííóþ ôîðìóëó, èìååì
1.64 10-4 =, îòêóäà P = 51.2 àòì.
Ïðèìåð 9-3. Êîíñòàíòà ðàâíîâåñèÿ ðåàêöèè
CO(ã) + 2H2(ã) = CH3OH(ã)
ïðè 500 K ðàâíà KP = 6.09 10-3. Ðåàêöèîííàÿ ñìåñü, ñîñòîÿùàÿ èç 1 ìîëü CO, 2 ìîëü H2 è 1 ìîëü èíåðòíîãî ãàçà (N2) íàãðåòà äî 500 K è îáùåãî äàâëåíèÿ 100 àòì. Ðàññ÷èòàòü ñîñòàâ ðàâíîâåñíîé ñìåñè.
Ðåøåíèå. Ïóñòü ïðîðåàãèðîâàëî ìîëü CO. Òîãäà
Ñëåäîâàòåëüíî, KX = è KP = KX.P-2 = .
Òàêèì îáðàçîì, 6.09 10-3 = .
Ðåøàÿ ýòî óðàâíåíèå, ïîëó÷àåì = 0.732. Ñîîòâåòñòâåííî, ìîëüíûå äîëè âåùåñòâ â ðàâíîâåñíîé ñìåñè ðàâíû: = 0.288, = 0.106, = 0.212 è = 0.394.
Ïðèìåð 9-4. Äëÿ ðåàêöèè
N2(ã) + 3H2(ã) = 2NH3(ã)
ïðè 298 Ê KP = 6.0 105, à fHo(NH3) = -46.1 êÄæ. ìîëü-1. Îöåíèòü çíà÷åíèå êîíñòàíòû ðàâíîâåñèÿ ïðè 500 Ê.
Ðåøåíèå. Ñòàíäàðòíàÿ ìîëüíàÿ ýíòàëüïèÿ ðåàêöèè ðàâíà
rHo= 2fHo(NH3) = -92.2 êÄæ. ìîëü-1.
Ñîãëàñíî óðàâíåíèþ (9.14), =
= ln (6.0 105) + = -1.73, îòêóäà K2 = 0.18.
Îòìåòèì, ÷òî êîíñòàíòà ðàâíîâåñèÿ ýêçîòåðìè÷åñêîé ðåàêöèè óìåíüøàåòñÿ ñ ðîñòîì òåìïåðàòóðû, ÷òî ñîîòâåòñòâóåò ïðèíöèïó Ëå Øàòåëüå.
ÇÀÄÀ×È
Óêàçàíèå: âî âñåõ çàäà÷àõ ñ÷èòàòü ãàçû èäåàëüíûìè.
- Ïðè 1273 Ê è îáùåì äàâëåíèè 30 àòì â ðàâíîâåñíîé ñìåñè
CO2(ã) + C(òâ) = 2CO(ã)
ñîäåðæèòñÿ 17% (ïî îáúåìó) CO2. Ñêîëüêî ïðîöåíòîâ CO2 áóäåò ñîäåðæàòüñÿ â ãàçå ïðè îáùåì äàâëåíèè 20 àòì? Ïðè êàêîì äàâëåíèè â ãàçå áóäåò ñîäåðæàòüñÿ 25% CO2?
- Ïðè 2000oC è îáùåì äàâëåíèè 1 àòì 2% âîäû äèññîöèèðîâàíî íà âîäîðîä è êèñëîðîä. Ðàññ÷èòàòü êîíñòàíòó ðàâíîâåñèÿ ðåàêöèè
H2O(ã) = H2(ã) + 1/2O2(ã) ïðè ýòèõ óñëîâèÿõ.
- Êîíñòàíòà ðàâíîâåñèÿ ðåàêöèè
CO(ã) + H2O(ã) = CO2(ã) + H2(ã)
ïðè 500oC ðàâíà Kp = 5.5. Ñìåñü, ñîñòîÿùàÿ èç 1 ìîëü CO è 5 ìîëü H2O, íàãðåëè äî ýòîé òåìïåðàòóðû. Ðàññ÷èòàòü ìîëüíóþ äîëþ H2O â ðàâíîâåñíîé ñìåñè.
- Êîíñòàíòà ðàâíîâåñèÿ ðåàêöèè
N2O4(ã) = 2NO2(ã)
ïðè 25oC ðàâíà Kp = 0.143. Ðàññ÷èòàòü äàâëåíèå, êîòîðîå óñòàíîâèòñÿ â ñîñóäå îáúåìîì 1 ë, â êîòîðûé ïîìåñòèëè 1 ã N2O4 ïðè ýòîé òåìïåðàòóðå.
- Ñîñóä îáúåìîì 3 ë, ñîäåðæàùèé 1.79 10-2 ìîëü I2, íàãðåëè äî 973 K. Äàâëåíèå â ñîñóäå ïðè ðàâíîâåñèè îêàçàëîñü ðàâíî 0.49 àòì. Ñ÷èòàÿ ãàçû èäåàëüíûìè, ðàññ÷èòàòü êîíñòàíòó ðàâíîâåñèÿ ïðè 973 K äëÿ ðåàêöèè
I2 (ã) = 2I (ã).
- Äëÿ ðåàêöèè
PCl5(ã) = PCl3(ã) + Cl2(ã)
ïðè 250oC rGo = -2508 Äæ. ìîëü-1. Ïðè êàêîì îáùåì äàâëåíèè ñòåïåíü ïðåâðàùåíèÿ PCl5 â PCl3 è Cl2 ïðè 250o C ñîñòàâèò 30%?
- Äëÿ ðåàêöèè
2HI(ã) = H2(ã) + I2(ã)
êîíñòàíòà ðàâíîâåñèÿ KP = 1.83 10-2 ïðè 698.6 Ê. Ñêîëüêî ãðàììîâ HI îáðàçóåòñÿ ïðè íàãðåâàíèè äî ýòîé òåìïåðàòóðû 10 ã I2 è 0.2 ã H2 â òðåõëèòðîâîì ñîñóäå? ×åìó ðàâíû ïàðöèàëüíûå äàâëåíèÿ H2, I2 è HI?
- Ñîñóä îáúåìîì 1 ë, ñîäåðæàùèé 0.341 ìîëü PCl5 è 0.233 ìîëü N2, íàãðåëè äî 250oC. Îáùåå äàâëåíèå â ñîñóäå ïðè ðàâíîâåñèè îêàçàëîñü ðàâíî 29.33 àòì. Ñ÷èòàÿ âñå ãàçû èäåàëüíûìè, ðàññ÷èòàòü êîíñòàíòó ðàâíîâåñèÿ ïðè 250oC äëÿ ïðîòåêàþùåé â ñîñóäå ðåàêöèè
PCl5 (ã) = PCl3 (ã) + Cl2(ã)
- Êîíñòàíòà ðàâíîâåñèÿ ðåàêöèè
CO(ã) + 2H2(ã) = CH3OH(ã)
ïðè 500 K ðàâíà KP = 6.09 10-3. Ðàññ÷èòàòü îáùåå äàâëåíèå, íåîáõîäèìîå äëÿ ïîëó÷åíèÿ ìåòàíîëà ñ 90% âûõîäîì, åñëè CO è H2 âçÿòû â ñîîòíîøåíèè 1: 2.
- Ïðè 25oC fGo(NH3) = -16.5 êÄæ. ìîëü-1. Ðàññ÷èòàòü rG ðåàêöèè îáðàçîâàíèÿ NH3 ïðè ïàðöèàëüíûõ äàâëåíèÿõ N2, H2 è NH3, ðàâíûõ 3 àòì, 1 àòì è 4 àòì ñîîòâåòñòâåííî.  êàêóþ ñòîðîíó ðåàêöèÿ áóäåò èäòè ñàìîïðîèçâîëüíî ïðè ýòèõ óñëîâèÿõ?
- Ýêçîòåðìè÷åñêàÿ ðåàêöèÿ
CO(ã) + 2H2(ã) = CH3OH(ã)
íàõîäèòñÿ â ðàâíîâåñèè ïðè 500 K è 10 áàð. Åñëè ãàçû èäåàëüíûå, êàê ïîâëèÿþò íà âûõîä ìåòàíîëà ñëåäóþùèå ôàêòîðû: à) ïîâûøåíèå T; á) ïîâûøåíèå P; â) äîáàâëåíèå èíåðòíîãî ãàçà ïðè V = const; ã) äîáàâëåíèå èíåðòíîãî ãàçà ïðè P = const; ä) äîáàâëåíèå H2 ïðè P = const?
- Êîíñòàíòà ðàâíîâåñèÿ ãàçîôàçíîé ðåàêöèè èçîìåðèçàöèè áîðíåîëà (C10H17OH) â èçîáîðíåîë ðàâíà 0.106 ïðè 503 K. Ñìåñü 7.5 ã áîðíåîëà è 14.0 ã èçîáîðíåîëà ïîìåñòèëè â ñîñóä îáúåìîì 5 ë è âûäåðæèâàëè ïðè 503 K äî äîñòèæåíèÿ ðàâíîâåñèÿ. Ðàññ÷èòàòü ìîëüíûå äîëè è ìàññû áîðíåîëà è èçîáîðíåîëà â ðàâíîâåñíîé ñìåñè.
- Ðàâíîâåñèå â ðåàêöèè
2NOCl(ã) = 2NO(ã) + Cl2(ã)
óñòàíàâëèâàåòñÿ ïðè 227oC è îáùåì äàâëåíèè 1.0 áàð, êîãäà ïàðöèàëüíîå äàâëåíèå NOCl ðàâíî 0.64 áàð (èçíà÷àëüíî ïðèñóòñòâîâàë òîëüêî NOCl). Ðàññ÷èòàòü rGoäëÿ ðåàêöèè. Ïðè êàêîì îáùåì äàâëåíèè ïàðöèàëüíîå äàâëåíèå Cl2 áóäåò ðàâíî 0.10 áàð?
- Ðàññ÷èòàòü îáùåå äàâëåíèå, êîòîðîå íåîáõîäèìî ïðèëîæèòü ê ñìåñè 3 ÷àñòåé H2 è 1 ÷àñòè N2, ÷òîáû ïîëó÷èòü ðàâíîâåñíóþ ñìåñü, ñîäåðæàùóþ 10% NH3 ïî îáúåìó ïðè 400oC. Êîíñòàíòà ðàâíîâåñèÿ äëÿ ðåàêöèè
N2(ã) + 3H2(ã) = 2NH3(ã)
ïðè 400oC ðàâíà K = 1.60 10-4.
- Ïðè 250oC è îáùåì äàâëåíèè 1 àòì PCl5 äèññîöèèðîâàí íà 80% ïî ðåàêöèè
PCl5 (ã) = PCl3 (ã) + Cl2(ã).
×åìó áóäåò ðàâíà ñòåïåíü äèññîöèàöèè PCl5, åñëè â ñèñòåìó äîáàâèòü N2, ÷òîáû ïàðöèàëüíîå äàâëåíèå àçîòà áûëî ðàâíî 0.9 àòì? Îáùåå äàâëåíèå ïîääåðæèâàåòñÿ ðàâíûì 1 àòì.
- Ïðè 2000oC äëÿ ðåàêöèè
N2(ã) + O2(ã) = 2NO(ã)
Kp = 2.5 10-3.  ðàâíîâåñíîé ñìåñè N2, O2, NO è èíåðòíîãî ãàçà ïðè îáùåì äàâëåíèè 1 áàð ñîäåðæèòñÿ 80% (ïî îáúåìó) N2 è 16% O2. Ñêîëüêî ïðîöåíòîâ ïî îáúåìó ñîñòàâëÿåò NO? ×åìó ðàâíî ïàðöèàëüíîå äàâëåíèå èíåðòíîãî ãàçà?
- Ðàññ÷èòàòü ñòàíäàðòíóþ ýíòàëüïèþ ðåàêöèè, äëÿ êîòîðîé êîíñòàíòà ðàâíîâåñèÿ
à) óâåëè÷èâàåòñÿ â 2 ðàçà, á) óìåíüøàåòñÿ â 2 ðàçà ïðè èçìåíåíèè òåìïåðàòóðû îò 298 Ê äî 308 Ê.
- Îêñèä ðòóòè äèññîöèèðóåò ïî ðåàêöèè
2HgO(òâ) = 2Hg(ã) + O2(ã).
Ïðè 420oC äàâëåíèå ãàçîâ ðàâíî 5.16 104 Ïà, à ïðè 450oC 10.8 104 Ïà. Ðàññ÷èòàòü êîíñòàíòû ðàâíîâåñèÿ ïðè ýòèõ òåìïåðàòóðàõ è ýíòàëüïèþ äèññîöèàöèè íà ìîëü HgO.
- Äëÿ ðåàêöèè
Ag2CO3(òâ) = Ag2O(òâ) + CO2(ã)
ïîëó÷åíû ñëåäóþùèå äàííûå ïî çàâèñèìîñòè êîíñòàíòû ðàâíîâåñèÿ îò òåìïåðàòóðû:
T, K
350
400
450
500
KP
3.98 10-4
1.41 10-2
1.86 10-1
1.48
Îïðåäåëèòü ñòàíäàðòíóþ ýíòàëüïèþ ðåàêöèè â ýòîì òåìïåðàòóðíîì èíòåðâàëå.
- Çàâèñèìîñòü êîíñòàíòû ðàâíîâåñèÿ ðåàêöèè 2C3H6(ã) = C2H4(ã) + C4H8(ã) îò òåìïåðàòóðû ìåæäó 300 Ê è 600 Ê îïèñûâàåòñÿ óðàâíåíèåì
ln K = -1.04 -1088 /T +1.51 105 /T2.
Ðàññ÷èòàòü rGo, rHoè rSoðåàêöèè ïðè 400 Ê.
Источник
