В замкнутом сосуде установилось равновесие

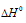
Задача 350.
Реакция СО + С12 ⇔ СОС12 протекает в закрытом сосуде при постоянной температуре; исходные вещества взяты в эквивалентных количествах. К моменту наступления равновесия остается 50% начального количества СО. Определить давление равновесной газовой смеси, если первоначальное давление равнялось 100 кПа (750 мм рт. ст.).
Решение:
Уравнение реакции имеет вид:

СО + С12 ⇔ СОС12

По условию задачи в реакцию вступило 50% СО. Из уравнения реакции следует, что из 1 моля СО и 1 моля С12 образуется 1 моль СОС12. Следовательно, из 0,5 моль СО и 0,5 моль С12 образовалось тоже 0,5 молей СОС12. Учитывая, что вещества реагируют друг с другом в эквивалентных количествах, значит, в 1л реакционной смеси содержится 2 моля исходных веществ (СО и С12), половина из которых прореагировало с образованием 0,5 молей СОС12.

Таким образом, количество системы уменьшилось на 0,5 молей и составило после протекания реакции 1,5 молей (2 – 0,5 = 1,5). Следовательно, давление равновесной газовой смеси определится из пропорции:

2 : 1,5 = 100 : х; х = (1,5 . 100)/2 = 75 кПа.

Ответ: 75кПа.

Задача 351.
В закрытом сосуде установилось равновесие: СО2(г.) + Н2(г.) ⇔ СО(г.) + +Н2О(г.); константа равновесия равна единице. Определить: а) сколько процентов СО2 подвергнется превращению в СО при данной температуре, если смешать 1 моль СО2 и 5 молей Н2? б) в каких объемных соотношениях были смешаны СО2 и Н2, если к моменту наступления равновесия в реакцию вступило 90% первоначального количества водорода?
Решение:
а) Уравнение реакции имеет вид

СО2(г.) + Н2(г.) ⇔ СО(г.) + +Н2О(г.)

Из уравнения следует, что из 1 моля СО2 и 1 моля Н2 образуется по 1 молю СО и Н2О.

Обозначим равновесную концентрацию СО и Н2О через х, тогда [CO] = [H2O]. Таким образом, равновесные концентрации СО2 и Н2 будут составлять, соответственно, (1 – х) и (5 – х)моль/л, а СО и Н2О – по х моль/л. Подставим эти значения в выражение константы равновесия реакции:

Таким образом, 83,3% СО2 подвергнется разложению в СО, учитывая, что [CO2] = 1 моль/л.

б) Находим количество Н2, которое вступило в реакцию: 5 . 0,9 = 4,5 моль/л. Остаток количества СО2 и Н2 одинаков и будет составлять 0,5 моль/л (5 – 4,5 = 0,5). Тогда объёмные соотношения СО2 и Н2, к моменту наступления равновесия, составляют:

V(H2) : V(CO2) = 4,5 : 0,5 = 9 : 1 .

Ответ: а) 83,3%; б) 9:1.

Задача 352.
При состоянии равновесия в системе:

N2(г) + 3H2(г) ⇔ 2NН3(г); = -92,4 кДж

концентрации участвующих веществ равны: [N2] = 3 моль/л; [H2] = 9 моль/л; [NН3] = 4 моль/л. Определить: а) исходные концентрации Н2 и N2 б) в каком направлении сместится равновесие с ростом температуры? в) в каком направлении сместится равновесие, если уменьшить объем реакционного сосуда?
Решение:
а) Для нахождения исходных концентраций веществ N2 и Н2 учтём, что, согласно уравнению реакции из 1 моля N2 и 3 молей Н2 образуется 2 моля NH3. Поскольку по условию задачи в каждом литре системы образовалось 4 моля NH3, то при этом было израсходовано 1/2 . 4 = 2 моля N2 и 3/4 . 4 = 6 молей Н2. Таким образом, искомые исходные концентрации N2 и Н2 равны:

[N2]0 = 3 + 2 = 5 моль/л;
[H2]0 = 6 + 3 = 9 моль/л.

б) Из уравнения реакции следует, что данная реакция экзотермическая, т.е. протекает с выделением теплоты. Поэтому при повышении температуры в экзотермической системе, согласно принципу Ле Шателье, равновесие системы сместится в сторону уменьшения действия температуры, т.е. влево.

в) Реакция протекает с уменьшением числа молей газообразных веществ, т.е. с уменьшением объёма и, соответственно, с уменьшением давления в системе. Поэтому при уменьшении объёма реакционного сосуда равновесие системы сместится в сторону образования аммиака, вправо, т.е. согласно принципу Ле Шателье, в сторону уменьшения действия (повышения давления при уменьшении объёма реакционного сосуда).

Ответ: а) [N2]0 = 5 моль/л, [H2]0 = 6 + 3 = 9 моль/л; б) влево; в) вправо.

Задача 353.
Константа равновесия реакции FeO(к) + CO(г) ⇔ Fe(к) + CO2(г), при некоторой температуре равна 0,5. Найти равновесные концентрации СО и СО2, если начальные концентрации этих веществ составляли: [СО] = 0,05 моль/л, [СО2] = 0,01 моль/л.
Решение:
Для нахождения равновесных концентраций веществ учтем, что, согласно уравнению реакции из 1 моля СО образуется 1 моль СО2. Обозначим количество, прореагировавшего вещества СО за x моль. Учитывая, что моль СО2 образуется при реакции, то при этом равновесная концентрация СО будет равна (0,05 – х)моль/л, а СО2 – (0,01 + х) моль/л.

Таким образом, подставив в выражение константы равновесия реакции эти концентрации, найдём значение:

Отсюда искомые равновесные концентрации веществ равны:

[СО]равн. = 0,05 – 0,01 = 0,04 моль/л;
[СО2]равн. = 0,01 + 0,01 = 0,02 моль/л.

Ответ: [СО] = 04 моль/л; [СО2] = 0,02 моль/л.

Задача 354.
Равновесие в системе H2(г) + I2(г) ⇔ 2HI(г) установилось пи следующих концентрациях: [H2] = 0,025 моль/л; [I2] = 0,005 моль/л; [HI] = 0,09 моль/л. Определить исходные концентрации йода и водорода.
Решение:
Для нахождения исходных концентраций йода и водорода учтём, что согласно уравнению реакции, из 1 моля йода и 1 моля водорода образуется 2 моля йодоводорода. Поскольку по условию задачи в каждом литре системы образовалось 0,09 молей вещества HI, то при этом было затрачено 0,045 (0,09/2 = 0?045) молей H2 и, соответственно 0,045 молей I2.

Отсюда находим исходные концентрации водорода и йода:

[I2]исх. = 0,005 + 0,045 = 0.0 5моль/л;
[H2]исх. =.0,025 + 0,045 = 0,07 моль/л.

Ответ: [H2]исх. = 0,07 моль/л; [I2]исх. = 0.05 моль/л.

Задача 355.
При некоторой температуре равновесие в системе 2NO2 ⇔ 2NO + O2 установилось при следующих концентрациях: [NO2] = 0,006 моль/л; [NO] = 0,024 моль/л. Найти константу равновесия реакции и исходную концентрацию NO2.
Решение:
Константа равновесия данной реакции выражается уравнением:

Учитывая, что равновесная концентрация О2 будет составлять 1/2 концентрации NO, т.е. 0,012 моль/л (0,024/2 = 0,012), рассчитаем константу равновесия:

Для нахождения исходной концентрации NO2 учтём, что согласно уравнению реакции из 1 моля NO2 образуется 1 моль NO. Поскольку по условию задачи в каждом литре системы образовалось 0,024 моля NO, то при этом было израсходовано 0,024 моля NO2.

Таким образом, искомая исходная концентрация NO равна:

[NO2]исх. = 0,006 + 0,024 = 0,03 моль/л.

Ответ: К = 0,192; [NO2]исх. = 0,03 моль/л.

Источник

Задача 356.
Для реакции Н2(г) + Br2(г) = 2HBr(г) при некоторой температуре К = 1. Определить состав (в процентах по объему) равновесной реакционной смеси, если исходная смесь состояла из 3 молей Н2 и 2 молей Вг2.
Решение:
Уравнение реакции имеет вид:

Н2(г) + Br2(г) = 2HBr(г)

Согласно уравнению реакции из 1 моля Н2 и 1 Br2 образуется 2 моль HBr. Обозначим количество израсходованных исходных веществ через x. Тогда равновесные концентрации реагирующих веществ будут раны:
[Н2] = (3 – х) моль/л, [Br2] = (2 – х) моль/л, [HBr] = (2х) моль/л. Подставив эти значения концентраций в выражение константы равновесия реакции, рассчитаем значение x:

Тогда равновесные концентрации веществ будут равны:

[Н2] = 3 – 0,808 = 2,192 моль/л;
[Br2] = 2 – 0,808 = 1,192 моль/л;
[HBr] = 2 . 0,808 = 1,616 моль/л.

Находим объёмы газов в равновесной системе, учитывая, что 1 моль любого газа при нормальных условиях занимает 22,4л, получим:

Тогда общий объём газовой равновесной системы будет равен 112 л (49,1 + 26,7 + 36,2 = 112).
Теперь определим состав газов (в процентах по объему) равновесной реакционной смеси по формуле:

w% – объёмная доля вещества, выраженная в процентах, V(в-ва) – объём вещества, V(смеси) – общий объём газовой смеси.

Тогда

Ответ: 43,84% Н2; 23,84% Br2; 32,32%HBr.

Задача 357.
Константа равновесия реакции равна единице. Сколько процентов вещества А подвергнется превращению, если смешать З моля вещества А и 5 молей вещества В?
Решение:
Уравнение реакции имеет вид:

А(г) + В(г) = С(г) + D(г)

Согласно уравнению реакции из 1 моля вещества А и 1 моля вещества В образуется по 1 молю веществ С и D. Обозначим равновесные концентрации веществ С и D через x. Тогда равновесные концентрации веществ будут раны: [C] = [D] = моль/л, [A] = (3 – х)моль/л, [B] = (5 – х)моль/л. Подставив эти значения концентраций в выражение кон-станты равновесия реакции, рассчитаем значение x:

Теперь рассчитаем, сколько процентов вещества А подвергнется превращению из пропорции:

3 : 100 = 1,875 : x; x = (1,875 . 100)/3 = 62,5%

Ответ: 62,5%.

Задача 358.
После смешивания газов А и В в системе А(г) + В(г) = С(г) + D(г) устанавливается равновесие при следующих концентрациях: [B] = 0,05 моль/л; [C] = 0,02 моль/л. Константа равновесия реакции равна 4.102. Найти исходные концентрации веществ А и В.
Решение:
Уравнение реакции имеет вид:

А(г) + В(г) = С(г) + D(г) .

Согласно уравнению реакции из 1 моля вещества А и 1 моля вещества В образуется по 1 молю веществ С и D.
Поскольку по условию задачи в каждом литре системы образовалось 0,02 моля вещества С, то такое же количество образовалось вещества D, было израсходовано по 0,02 моля веществ А и В.

Сначала найдём концентрацию вещества А из выражения для константы равновесия реакции:

Отсюда рассчитаем искомые исходные концентрации веществ А и В:

[A]0 = 0,2 + 0,02 = 0,22 моль/л;
[B]0 = 0,05 + 0.02 = 0,07 моль/л.

Ответ: [A]0 = 0,22 моль/л; [B]0 = 0,07 моль/л.

Задача 359.
Найти константу равновесия реакции N2O4 ⇔ 2NO2, если начальная концентрация N2O4 составляла 0,08 моль/л, а к моменту наступления равновесия диссоциировало 50% N2O4.
Решение:
Уравнение реакции имеет вид: N2O4 ⇔ 2NO2. Из уравнения реакции следует, что из 1 моля N2O4 образуется 2 моля NO2. Поскольку по условию задачи 50% N2O4 диссоциировало, то количество N2O4, продиссоциировавшегося составляет 0,04 моль/л (0,08 . 0,5 = 0,04).

Тогда равновесные концентрации участвующих веществ будут равны:

[N2O4]0 = 0,08 – 0,04 = 0,04 моль/л;
[NO2]0 = 0,04 .2 = 0,08 моль/л

Выражение для константы равновесия для данной реакции будет иметь вид:

Подставляя в это выражение данные из задачи, получим:

Ответ: 0,16

Задача 360.
В замкнутом сосуде протекает реакция АВ(г) ⇔ А(г) + В(г) Константа равновесия реакции равна 0,04, а равновесная концентрация вещества В составляет 0,02 моль/л. Найти начальную концентрацию вещества АВ. Сколько процентов вещества АВ разложилось?
Решение:
Уравнение реакции имеет вид: АВ(г) ⇔ А(г) + В(г). Из уравнения реакции следует, что из 1 моля вещества АВ образуется 1 моль вещества А и 1 моль вещества В. Поскольку по условию задачи в каждом литре системы образовалось 0,02 моля вещества В, то столько же образовалось и вещества А, при этом было израсходовано 0,02 моля вещества АВ.

Константа равновесия данной реакции выражается уравнением

Подставляя в это выражение данные задачи, рассчитаем равновесную концентрацию вещества АВ:

Таким образом, искомая исходная концентрация вещества АВ будет равна:

[AB]0 = 0,02 + 0,01 = 0,03 моль/л

Сколько процентов вещества АВ разложилось находим из пропорции:

0,03 : 100 = 0,02 : х = (0,02 . 100)/0,03 = 66,7%

Ответ: [AB]0 = 0,03 моль/л; 66,67%.

Источник

СО + С12 ⇔ СОС12

2 : 1,5 = 100 : х; х = (1,5 . 100)/2 = 75 кПа.

Ответ: 75кПа.

Читайте также: Защитить сосуды от жары

СО2(г.) + Н2(г.) ⇔ СО(г.) + +Н2О(г.)

Из уравнения следует, что из 1 моля СО2 и 1 моля Н2 образуется по 1 молю СО и Н2О.

Таким образом, 83,3% СО2 подвергнется разложению в СО, учитывая, что [CO2] = 1 моль/л.

V(H2) : V(CO2) = 4,5 : 0,5 = 9 : 1 .

Ответ: а) 83,3%; б) 9:1.

Задача 352.
При состоянии равновесия в системе:

N2(г) + 3H2(г) ⇔ 2NН3(г); = -92,4 кДж

[N2]0 = 3 + 2 = 5 моль/л;
[H2]0 = 6 + 3 = 9 моль/л.

Ответ: а) [N2]0 = 5 моль/л, [H2]0 = 6 + 3 = 9 моль/л; б) влево; в) вправо.

Таким образом, подставив в выражение константы равновесия реакции эти концентрации, найдём значение:

Отсюда искомые равновесные концентрации веществ равны:

[СО]равн. = 0,05 – 0,01 = 0,04 моль/л;
[СО2]равн. = 0,01 + 0,01 = 0,02 моль/л.

Ответ: [СО] = 04 моль/л; [СО2] = 0,02 моль/л.

Отсюда находим исходные концентрации водорода и йода:

[I2]исх. = 0,005 + 0,045 = 0.0 5моль/л;
[H2]исх. =.0,025 + 0,045 = 0,07 моль/л.

Ответ: [H2]исх. = 0,07 моль/л; [I2]исх. = 0.05 моль/л.

Таким образом, искомая исходная концентрация NO равна:

[NO2]исх. = 0,006 + 0,024 = 0,03 моль/л.

Ответ: К = 0,192; [NO2]исх. = 0,03 моль/л.

Источник

Материалы портала onx.distant.ru

Понятие химического равновесия

Признаки химического равновесия

Принцип Ле Шателье

Влияние температуры на химическое равновесие

Влияние давления на химическое равновесие

Влияние концентрации на химическое равновесие

Константа химического равновесия

Примеры решения задач

Задачи для самостоятельного решения

Равновесным считается состояние системы, которое остается неизменным, причем это состояние не обусловлено действием каких-либо внешних сил. Состояние системы реагирующих веществ, при котором скорость прямой реакции становится равной скорости обратной реакции, называется химическим равновесием. Такое равновесие называется еще подвижным или динамическим равновесием.

Состояние системы остается неизменным во времени при сохранении внешних условий.
Равновесие является динамическим, то есть обусловлено протеканием прямой и обратной реакции с одинаковыми скоростями.
Любое внешнее воздействие вызывает изменение в равновесии системы; если внешнее воздействие снимается, то система снова возвращается в исходное состояние.
К состоянию равновесия можно подойти с двух сторон – как со стороны исходных веществ, так и со стороны продуктов реакции.
В состоянии равновесия энергия Гиббса достигает своего минимального значения.

Влияние изменения внешних условий на положение равновесия определяется принципом Ле Шателье (принципом подвижного равновесия):

Если на систему, находящуюся в состоянии равновесия, производить какое–либо внешнее воздействие, то в системе усилится то из направлений процесса, которое ослабляет эффект этого воздействия, и положение равновесия сместится в том же направлении.

Принцип Ле Шателье применим не только к химическим процессам, но и к физическим, таким как кипение, кристаллизация, растворение и т. д.

Рассмотрим влияние различных факторов на химическое равновесие на примере реакции окисления NO:

2NO(г) + O2(г) → 2NO2(г); ΔHо298 = — 113,4 кДж/моль.

При повышении температуры равновесие сдвигается в сторону эндотермической реакции, при понижении температуры – в сторону экзотермической реакции.

Степень смещения равновесия определяется абсолютной величиной теплового эффекта: чем больше по абсолютной величине энтальпия реакции ΔH, тем значительнее влияние температуры на состояние равновесия.

В рассматриваемой реакции синтеза оксида азота (IV) повышение температуры сместит равновесие в сторону исходных веществ.

Сжатие смещает равновесие в направлении процесса, который сопровождается уменьшением объема газообразных веществ, а понижение давления сдвигает равновесие в противоположную сторону.

В рассматриваемом примере в левой части уравнения находится три объема, а в правой – два. Так как увеличение давления благоприятствует процессу, протекающему с уменьшением объема, то при повышении давления равновесие сместится вправо, т.е. в сторону продукта реакции – NO2. Уменьшение давления сместит равновесие в обратную сторону. Следует обратить внимание на то, что, если в уравнении обратимой реакции число молекул газообразных веществ в правой и левой частях равны, то изменение давления не оказывает влияния на положение равновесия.

Для рассматриваемой реакции введение в равновесную систему дополнительных количеств NO или O2 вызывает смещение равновесия в том направлении, при котором концентрация этих веществ уменьшается, следовательно, происходит сдвиг равновесия в сторону образования NO2. Увеличение концентрации NO2 смещает равновесие в сторону исходных веществ.

Катализатор одинаково ускоряет как прямую, так и обратную реакции и поэтому не влияет на смещение химического равновесия.

При введении в равновесную систему (при Р = const) инертного газа концентрации реагентов (парциальные давления) уменьшаются. Поскольку рассматриваемый процесс окисления NO идет с уменьшением объема, то при добавлении инертного газа равновесие сместится в сторону исходных веществ.

Для химической реакции:

2NO(г) + O2(г) → 2NO2(г)

константа химической реакции Кс есть отношение:

Кс = [NO2]2/([NO]2 · [O2]) (1)

В этом уравнении в квадратных скобках – концентрации реагирующих веществ, которые устанавливаются при химическом равновесии, т.е. равновесные концентрации веществ.

Константа химического равновесия связана с изменением энергии Гиббса уравнением:

ΔGTо = – RTlnK (2)

Задача 1. При некоторой температуре равновесные концентрации в системе 2CO (г) + O2 (г)→2CO2 (г) составляли: [CO] = 0,2 моль/л, [O2] = 0,32 моль/л, [CO2] = 0,16 моль/л. Определите константу равновесия при этой температуре и исходные концентрации CO и O2, если исходная смесь не содержала СО2.

Решение.

2CO(г) + O2(г) →2CO2(г)

Вещество	CO	O2	CO2
Сисходн, моль/л	0,52	0,48
Спрореагир,моль/л	0,32	0,16	0,16
Сравн, моль/л	0,2	0,32	0,16

Во второй строке под Спрореагир понимается концентрация прореагировавших исходных веществ и концентрация образующегося CO2, причем, Сисходн= Спрореагир + Сравн.

Задача 2. Используя справочные данные, рассчитайте константу равновесия процесса

3 H2 (г) + N2 (г) →2 NH3 (г) при 298 К.

Решение.

ΔG298о = 2·(- 16,71) кДж = -33,42·103 Дж.

ΔGTо = — RTlnK.

lnK = 33,42·103/(8,314× 298) = 13,489. K = 7,21× 105.

Задача 3. Определите равновесную концентрацию HI в системе

H2(г) + I2(г) →2HI(г),

если при некоторой температуре константа равновесия равна 4, а исходные концентрации H2 , I2 и HI равны, соответственно, 1, 2 и 0 моль/л.

Решение. Пусть к некоторому моменту времени прореагировало x моль/л H2.

Вещество	H2	I2	HI
сисходн., моль/л	1	2
спрореагир., моль/л	x	x	2x
cравн., моль/л	1-x	2-x	2x

Тогда, К = (2х)2/((1-х)(2-х))

Решая это уравнение, получаем x = 0,67.

Значит, равновесная концентрация HI равна 2× 0,67 = 1,34 моль/л.

Задача 4. Используя справочные данные, определите температуру, при которой константа равновесия процесса: H2(г) + HCOH(г) →CH3OH(г) становится равной 1. Принять, что ΔНоТ » ΔНо298, а ΔSоT » ΔSо298.

Решение.

Если К = 1, то ΔGоT = — RTlnK = 0;

ΔGоT = ΔНо298 — ТΔ Sо298 .

ΔНо298 = -202 – (- 115,9) = -86,1 кДж = — 86,1× 103 Дж;

ΔSо298 = 239,7 – 218,7 – 130,52 = -109,52 Дж/К;

0 = — 86100 — Т·(-109,52)

Т = 786,15К

Задача 5. Для реакции SO2(Г) + Cl2(Г) →SO2Cl2(Г) при некоторой температуре константа равновесия равна 4. Определите равновесную концентрацию SO2Cl2, если исходные концентрации SO2, Cl2 и SO2Cl2 равны 2, 2 и 1 моль/л соответственно.

Решение. Пусть к некоторому моменту времени прореагировало x моль/л SO2.

SO2(г) + Cl2(г) →SO2Cl2(г)

Вещество	SO2	Cl2	SO2Cl2
cисходн., моль/л	2	2	1
cпрореагир., моль/л	x	x	х
cравн., моль/л	2-x	2-x	x + 1

Тогда получаем:

(х + 1)/(2 — х)2 = 4

Решая это уравнение, находим: x1 = 3 и x2 = 1,25. Но x1 = 3 не удовлетворяет условию задачи.

Следовательно, [SO2Cl2] = 1,25 + 1 = 2,25 моль/л.

1. В какой из приведенных реакций повышение давления сместит равновесие вправо? Ответ обоснуйте.

1) 2 NH3 (г) → 3H2 (г) + N2 (г)

2) ZnCO3 (к) → ZnO(к) + CO2 (г)

3) 2HBr (г) → H2 (г) + Br2 (ж)

4) CO2 (г) + C (графит) →2CO (г)

Так как увеличение давления благоприятствует процессу, протекающему с уменьшением количества
газообразных веществ, то равновесие сместится вправо в реакции 3.

2. При некоторой температуре равновесные концентрации в системе:

2HBr (г) →H2 (г) + Br2 (г)

составляли: [HBr] = 0,3 моль/л, [H2] = 0,6 моль/л, [Br2] = 0,6 моль/л. Определите константу равновесия и исходную концентрацию HBr.

3. Для реакции H2(г) + S(г) →H2S(г) при некоторой температуре константа равновесия равна 2. Определите равновесные концентрации H2 и S, если исходные концентрации H2, S и H2S равны, соответственно, 2, 3 и 0 моль/л.

4. Используя справочные данные, вычислите температуру, при которой константа равновесия процесса

CO2(г) + C(графит) →2CO(г)

становится равной 1. Примите, что ΔНоТ≈ΔНо298, а ΔSоT≈ΔSо298

5. Используя справочные данные, рассчитайте константу равновесия процесса:

С2Н4(г) →С2Н2(г) + Н2(г)при 298 К

6. Для реакции 2С3Н8(г) → н-С5Н12(г)+СН4(г) при температуре 1000 К константа равновесия равна 4. Определите равновесную концентрацию н-пентана, если исходная концентрация пропана равна 5 моль/л.

7. При температуре 500 К константа равновесия процесса:

СО2(г) + 3Н2(г) → СН3ОН(г) + Н2О(г)

равна 3,4·10-5. Вычислите Δ Gо500.

8. При температуре 800 К константа равновесия процесса н-С6Н14(г)+ 2С3Н6(г)+Н2(г) равна 8,71. Определите ΔGоf,800(С3Н6(г)), если ΔGоf,800(н-С6Н14(г)) = 305,77 кДж/моль.

9. Для реакции СО(г) + Cl2(г) →СO2Cl2(г) при некоторой температуре равновесная концентрация СO2Cl2(г) равна 1,2 моль/л. Определите константу равновесия данного процесса, если исходные концентрации СО(г) и Cl2(г) равны соответственно 2,0 и 1,8 моль/л.

10. При некоторой температуре равновесные концентрации в системе 2SО2(г) + О2(г) →2SO3(г) составляли: [SО2 ]=0,10 моль/л, [О2]=0,16 моль/л, [SО3]=0,08 моль/л. Вычислите константу равновесия и исходные концентрации SО2 и О2.

К=4,0; исходная концентрация SО2 составляет 0,18 моль/л;
исходная концентрация О2 составляет 0,20 моль/л.

Источник