Внутренняя энергия газа в сосуде
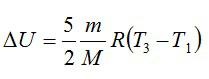
6.2. Первый закон термодинамики
6.2.1. Внутренняя энергия идеального газа
Внутренняя энергия любого вещества – это энергия теплового движения его молекул и энергия их взаимодействия между собой. Модель идеального газа предполагает отсутствие взаимодействия между его молекулами, поэтому внутренней энергией идеального газа принято считать только энергию теплового движения молекул. Внутренняя энергия газа представляет собой сумму кинетических энергий его молекул и определяется формулой
U = N ⟨ E k ⟩ ,
где N – число молекул (атомов), N = νN A; ν – количество вещества; N A – постоянная (число) Авогадро, N A = 6,02 ⋅ 1023 моль-1; ⟨ E k ⟩ – средняя кинетическая энергия одной молекулы, ⟨ E k ⟩ = i 2 k T ; i – число степеней свободы; k – постоянная Больцмана, k = 1,38 ⋅ 10−23 Дж/К; T – абсолютная температура.
Число степеней свободы зависит от количества атомов в молекуле газа и имеет следующие значения:
- для одноатомного –
i = 3;
- для двухатомного –
i = 5;
- для трех- и многоатомного –
i = 6.
В Международной системе единиц внутренняя энергия вещества (газа) измеряется в джоулях (1 Дж).
Внутренняя энергия идеального газа определяется формулой
U = i 2 ν R T ,
где i – число степеней свободы; ν – количество вещества (газа); R – универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T – абсолютная (термодинамическая) температура вещества.
Внутренняя энергия для одно-, двух-, трех- и многоатомных газов определяется следующими формулами:
- для одноатомного –
U = 3 2 ν R T ;
- для двухатомного –
U = 5 2 ν R T ;
- для трех- и многоатомного –
U = 3νRT.
Изменение внутренней энергии газа определяется разностью
ΔU = U 2 − U 1,
где U 1 – внутренняя энергия начального состояния газа; U 2 – внутренняя энергия конечного состояния газа.
Изменение внутренней энергии газа связано с изменением кинетической энергии движения его молекул. Изменение кинетической энергии движения молекул вещества, в свою очередь, связано с изменением температуры. Следовательно, изменение внутренней энергии газа определяется изменением его температуры.
Изменение внутренней энергии идеального газа рассчитывается по формуле
Δ U = i 2 ν R ( T 2 − T 1 ) = i 2 ν R Δ T ,
где i – число степеней свободы; ν – количество вещества; R – универсальная газовая постоянная, R ≈ 8,31 Дж/(моль ⋅ К); T 2 – абсолютная температура конечного состояния газа; T 1 – абсолютная температура начального состояния идеального газа; ∆T = T 2 − T 1.
Изменение внутренней энергии для одно-, двух-, трех- и многоатомных газов определяется следующими формулами:
- для одноатомного –
Δ U = 3 2 ν R Δ T ;
- для двухатомного –
Δ U = 5 2 ν R Δ T ;
- для трех- и многоатомного –
∆U = 3νR∆T.
Изменение внутренней энергии газа ΔU при различных процессах также различно и показано в таблице (для одно-, двух-, трех- и многоатомных газов):
Процесс | Одноатомный газ, i = 3 | Двухатомный газ, i = 5 | Трех- и многоатомный газ, i = 6 |
|---|---|---|---|
| Изотермический T = const | |||
| Изохорный V = const | 3 2 ν R Δ T | 5 2 ν R Δ T | 3νR∆T |
| Изобарный P = const | 3 2 ν R Δ T | 5 2 ν R Δ T | 3νR∆T |
| Циклический |
Внутренняя энергия газа не изменяется (U = const):
- при изотермическом процессе, так как ΔT = 0;
- при циклическом процессе, так как в конце процесса газ возвращается в состояние с исходными параметрами; циклическим (круговым, замкнутым) процессом, или циклом, называется процесс, при котором газ, пройдя ряд состояний, возвращается в исходное.
Пример 1. В ходе некоторого процесса давление и объем постоянной массы идеального одноатомного газа изменяются таким образом, что pV 2 = const, где p – давление в паскалях; V – объем в кубических метрах. Во сколько раз уменьшается внутренняя энергия газа при увеличении его объема в 3 раза?
Решение. Внутренняя энергия идеального одноатомного газа определяется следующей формулой:
- для начального состояния газа –
U 1 = 3 2 ν R T 1 ,
где ν – количество вещества (газа); R – универсальная газовая постоянная, R ≈ 8,31 Дж/(моль ⋅ К); T 1 – температура газа в начальном состоянии;
- для конечного состояния газа –
U 2 = 3 2 ν R T 2 ,
где T 2 – температура газа в конечном состоянии.
Искомым является отношение
U 1 U 2 = 3 ν R T 1 2 ⋅ 2 3 ν R T 2 = T 1 T 2 .
Найдем отношение температур.
Для этого из уравнения Менделеева – Клапейрона
pV = νRT
выразим давление
p = ν R T V
и подставим полученное выражение в заданный в условии задачи закон:
ν R T V ⋅ V 2 = ν R T V = const , или TV = const.
Заданное в условии соотношение между давлением и объемом эквивалентно полученному соотношению между температурой и объемом.
Для двух состояний газа справедливо тождество
T 1V 1 = T 2V 2,
где V 1 – объем газа в начальном состоянии; V 2 – объем газа в конечном состоянии.
Отсюда следует, что отношение температур определяется выражением
T 1 T 2 = V 2 V 1 ,
а искомое отношение внутренних энергий газа равно
U 1 U 2 = V 2 V 1 = 3 .
Пример 2. Термоизолированный сосуд, содержащий некоторое количество водорода, движется со скоростью 250 м/с. Как изменится температура газа, если сосуд внезапно остановить? Молярная масса водорода равна 2,0 г/моль. Теплоемкостью сосуда пренебречь.
Решение. Энергия газа в сосуде определяется суммой:
- для движущегося сосуда –
E 1 = U 1 + W k 1,
где U 1 – внутренняя энергия водорода (двухатомного газа) в движущемся сосуде (энергия теплового движения молекул водорода), U 1 = 5νRT 1/2; ν – количество водорода, ν = m/M; m – масса водорода; M – молярная масса водорода, M = 2,0 г/моль; T 1 – начальная температура водорода; R – универсальная газовая постоянная, R = = 8,31 Дж/(моль ⋅ К); W k 1 – кинетическая энергия водорода, движущегося вместе с сосудом, W k 1 = mv 2/2; v – скорость сосуда, v = 250 м/с;
- для остановившегося сосуда –
E 2 = U 2 + W k 2,
где U 2 – внутренняя энергия водорода (двухатомного газа) в остановившемся сосуде, U 2 = 5νRT 2/2; T 2 – конечная температура водорода; W k 2 – кинетическая энергия водорода, остановившегося вместе с сосудом, W k 2 = 0.
По условию задачи обмена энергией между газом в сосуде и окружающей средой не происходит, так как сосуд является термоизолированным; поэтому энергия газа сохраняется
E 1 = E 2,
или, в явном виде, –
U 1 + W k 1 = U 2 + W k 2.
Подстановка в полученное равенство выражений для внутренней и кинетической энергий газа в сосуде дает
5 m R T 1 2 M + m v 2 2 = 5 m R T 2 2 M .
Искомая разность температур определяется формулой
Δ T = v 2 M 5 R .
Вычислим:
Δ T = ( 250 ) 2 ⋅ 2,0 ⋅ 10 − 3 5 ⋅ 8,31 = 3,0 К.
При внезапной остановке сосуда, движущегося с указанной скоростью, температура содержащегося в нем водорода повышается на 3,0 К.
Источник
Определение
Числом степеней свободы механической системы называют количество независимых величин, с помощью которых может быть задано положение системы.
Внутренняя энергия идеального газа представляет собой сумму только кинетической энергии всех молекул, а потенциальной энергией взаимодействия можно пренебречь:
U=∑Ek0=NEk0=mNAM·ikT2=i2·mMRT=i2νRT=i2pV
i – степень свободы. i = 3 для одноатомного (или идеального) газа, i = 5 для двухатомного газа, i = 6 для трехатомного газа и больше.
Изменение внутренней энергии идеального газа в изопроцессах
| Основная формула | ΔU=32·mMRT=32νRT=32νR(T2−T1) |
| Изотермический процесс | ΔU=0 Температура при изотермическом процессе – величина постоянная. Так как внутренняя энергия идеального газа постоянной массы в замкнутой системе зависит только от изменения температуры, то она тоже остается постоянной. |
| Изобарное расширение | ΔU=32νR(T2−T1)=32(pV2−pV1)=32pΔV |
| Изохорное увеличение давления | ΔU=32νR(T2−T1)=32(p2V−p1V)=32VΔp |
| Произвольный процесс | ΔU=32νR(T2−T1)=32(p2V2−p1V1) |
Пример №1. На рисунке показан график циклического процесса, проведенного с идеальным газом. На каком из участков внутренняя энергия газа уменьшалась?
Внутренняя энергия газа меняется только при изменении температуры. Так как она прямо пропорциональная температуре, то уменьшается она тогда, когда уменьшается и температура. Температура падает на участке 3.
Работа идеального газа
Если газ, находящийся под поршнем, нагреть, то, расширяясь, он поднимет поршень, т.е. совершит механическую работу.
Механическая работа вычисляется по формуле:
A=Fscosα
Перемещение равно разности высот поршня в конечном и начальном положении:
s=h2−h1
Также известно, что сила равна произведению давления на площадь, на которое это давление оказывается. Учтем, что направление силы и перемещения совпадают. Поэтому косинус будет равен единице. Отсюда работа идеального газа равна произведению давления на площадь поршня:
Работа идеального газа
F=pS
p – давление газа, S – площадь поршня
Работа, необходимая для поднятия поршня – полезная работа. Она всегда меньше затраченной работы, которая определяется изменением внутренней энергии идеального газа при изобарном расширении:
A’=p(V2−V1)=pΔV>0
Внимание! Знак работы определяется только знаком косинуса угла между направлением силы, действующей на поршень, и перемещением этого поршня.
Работа идеального газа при изобарном сжатии:
A’=p(V2−V1)=pΔV<0
Работа идеального газа при нагревании газа:
A’=νRΔT=νR(T2−T1)=mMνRΔT
Внимание! В изохорном процессе работа, совершаемая газом, равна нулю, так как работа газа определяется изменением его объема. Если изменения нет, работы тоже нет.
Геометрический смысл работы в термодинамике
В термодинамике для нахождения работы можно вычислить площадь фигуры под графиком в осях (p, V).
Примеры графических задач
| Изобарное расширение: A’=p(V2−V1) A’>0 |
| Изобарное сжатие: A’=p(V2−V1) A'<0 |
| Изохорное охлаждение: V=const A’=0 |
Изохорное охлаждение и изобарное сжатие: 1-2: A’=0 2-3: A’=pΔV<0 |
| Замкнутый цикл: 1-2: A’>0 2-3: A’=0 3-4: A'<0 4-1: A’=0 A’=(p1−p3)(V2−V1) |
| Произвольный процесс: A’=p1+p22(V2−V1) |
Пример №2. На pV-диаграмме показаны два процесса, проведенные с одним и тем же количеством газообразного неона. Определите отношение работ A2 к A1 в этих процессах.
Неон – идеальный газ. Поэтому мы можем применять формулы, применяемые для нахождения работы идеального газа. Работа равна площади фигуры под графиком. С учетом того, что в обоих случаях изобарное расширение, получим:
A2=p(V2−V1)=4p(5V−3V)=4p2V=8pV
A1=p(V2−V1)=p(5V−V)=4pV
Видно, что работа, совершенная во втором процессе, вдвое больше работы, совершенной газом в первом процессе.
Задание EF17505 Идеальный одноатомный газ переходит из состояния 1 в состояние 2 (см. диаграмму). Масса газа не меняется. Как изменяются при этом следующие три величины: давление газа, его объём и внутренняя энергия?
Для каждой величины подберите соответствующий характер изменения:
1) увеличивается
2) уменьшается
3) не изменяется
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
- Определить по графику, как меняется давление.
- Определить, как меняется объем.
- Определить, отчего зависит внутренняя энергия газа, и как она меняется в данном процессе.
Решение
На графике идеальный одноатомный газ изотермически сжимают, так как температура остается неизменной, а давление увеличивается. При этом объем должен уменьшаться. Но внутренняя энергия идеального газа определяется его температурой. Так как температура постоянна, внутренняя энергия не изменяется.
Ответ: 123
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF17758
Один моль аргона, находящийся в цилиндре при температуре T1=600 K и давлении p1=4⋅105 Па, расширяется и одновременно охлаждается так, что его температура при расширении обратно пропорциональна объёму. Конечное давление газа p2=105 Па. Какое количество теплоты газ отдал при расширении, если при этом он совершил работу A=2493 Дж?
Алгоритм решения
1.Записать исходные данные.
2.Записать уравнение состояния идеального газа.
3.Записать формулу для расчета внутренней энергии газа.
4.Используя первое начало термодинамики, выполнить общее решение задачи.
5.Подставив известные данные, вычислить неизвестную величину.
Решение
Запишем исходные данные:
• Начальная температура газа: T1 = 600 К.
• Начальное давление: p1 = 4∙105Па.
• Конечное давление: p2 = 105Па.
• Работа, совершенная газом: A = 2493 Дж.
Аргон является одноатомным газом. Поэтому для него можно использовать уравнение состояния идеального газа:
pV=νRT
Внутренняя энергия одноатомного идеального газа пропорциональна температуре:
U=32νRT
Внутренняя энергия аргона до расширения и после него:
U1=32νRT1
U2=32νRT2
Согласно условию задачи, температура при расширении обратно пропорциональна объёму. Следовательно:
T=constV
T1V1=T2V2
Выразим конечную температуру:
T2=T1V1V2
Составим уравнение состояния газа для состояний аргона 1 и 2:
p1V1=νRT1
p2V2=νRT2
Отсюда:
νR=p1V1T1=p2V2T2
Отсюда отношение объема аргона в состоянии 1 к объему газа в состоянии 2 равно:
V1V2=p2T1p1T2
Подставим это отношение в формулу для конечной температуры:
T2=T1V1V2=p2T12p1T2
Отсюда:
T2=T1√p2p1
Отсюда внутренняя энергия газа в состоянии 2 равна:
U2=32νRT1√p2p1
Уменьшение внутренней энергии аргона составило (изначально она была выше):
ΔU=U1−U2=32νRT1−32νRT1√p2p1=32νRT1(1−√p2p1)
В соответствии с первым началом термодинамики уменьшение внутренней энергии равно сумме совершённой работы и количества теплоты, отданного газом:
ΔU=Q+A
Следовательно, газ отдал следующее количество теплоты:
Q=ΔU−A=32νRT1(1−√p2p1)−A
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF17966 Идеальный газ переводят из состояния 1 в состояние 3 так, как показано на графике зависимости давления газа от объёма. Работа, совершённая при этом газом, равна
Ответ:
а) р0V0
б) 2р0V0
в) 4р0V0
г) 6р0V0
Алгоритм решения
1.Определить, на каком участке графика совершается работа.
2.Записать геометрический смысл работы.
3.Извлекая данные из графика, вычислить работу, совершенную газом.
Решение
Работа совершается только тогда, когда газ меняет объем. Поэтому работа совершается только на участке 1-2.
Работа идеального газа равна площади фигуры, заключенной под графиком термодинамического процесса в координатах (p, V).
Давление газа при этом равно 2p0, а объем равен разности 2V0и V0. Следовательно, работа, совершенная газом, будет равна произведению:
A=2p0(2V0−V0)=2p0V0
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алиса Никитина | ???? Скачать PDF | Просмотров: 3.3k | Оценить:
Источник
Решение задач – занятие, которое любит далеко не каждый. Здесь мы стараемся сделать так, чтобы оно занимало у вас поменьше времени без ущерба для качества самого решения. Тема этой статьи – задачи на внутреннюю энергию.
Подписывайтесь на наш телеграм и читайте полезные материалы для студентов каждый день!
Решение задач: внутренняя энергия
Прежде чем приступать к задачам на внутреннюю энергию тела, посмотрите общую памятку по решению физических задач. И пусть под рукой на всякий случай всегда будут основные физические формулы.
Задача №1. Изменение внутренней энергии
Условие
Воздушный шар объёмом 500 м3 наполнен гелием под давлением 105 Па. В результате нагрева температура газа в аэростате поднялась от 10 °С до 25 °С. Как увеличилась внутренняя энергия газа?
Решение
Для решения будем использовать формулу внутренней энергии идеального газа:
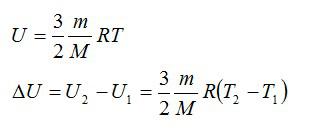
Массу гелия выразим из уравнения Клапейрона-Менделеева:
Тогда можно записать:
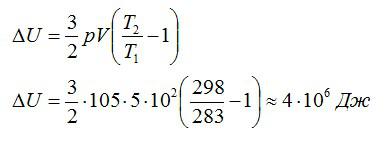
Ответ: 4 МДж.
Задача №2. Внутренняя энергия и работа
Условие
Азот массой 200 г расширяется изотермически при температуре 280 К, причем объём газа увеличивается в 2 раза. Найти:
- Изменение ∆U внутренней энергии газа.
- Совершенную при расширении газа работу А.
- Количество теплоты Q, полученное газом.
Решение
Так как процесс изотермический, то изменение внутренней энергии равно нулю, а работа равна количеству теплоты, полученному газом:
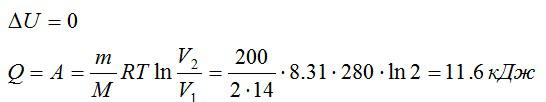
Ответ: 0; 11,6 кДж; 11,6 кДж.
Задача №3. Изменение внутренней энергии при изобарном и изохорном процессе
Условие
Кислород занимает объём V1= 3 л при давлении p1= 820 кПа. В результате изохорного нагревания и изобарного расширения газ переведён в состояние с объёмом V2= 4,5 л и давлением p2= 600 кПа. Найти количество теплоты, полученное газом; изменение внутренней энергии газа.
Решение
Теплота, подведенная к газу, идет на совершение работы и изменение внутренней энергии:
В изохорном и изобарном процессе соответственно:
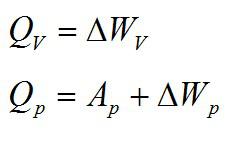
Изохорное нагревание:
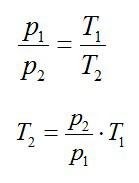
Изменение внутренней энергии при изохорном процессе:
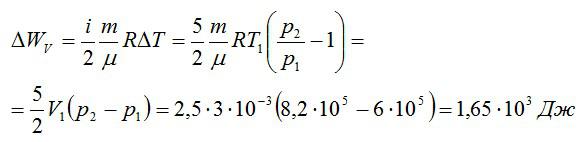
Изменение внутренней энергии при изобарном процессе:
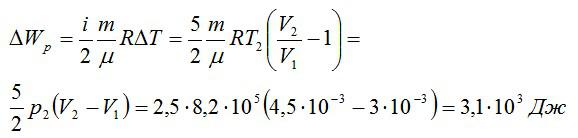
Общее изменение внутренней энергии:
Ответ: 4,75 кДж.
Задача №4. Изменение внутренней энергии двухатомного газа
Условие
Кислород массой 2 кг занимает объём 6 м3 и находится под давлением 1 атм. Газ был нагрет сначала при постоянном давлении до объёма 13 м3, а затем при постоянном объёме – до давления 23 атм. Найти изменение внутренней энергии газа.
Решение
Изменение внутренней энергии находим по формуле:
Эту форму можно преобразовать, используя уравнение Клапейрона-Менделеева:
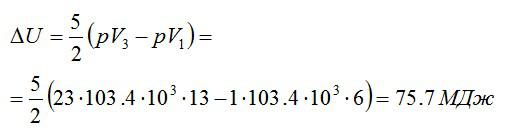
Ответ: 75,7 МДж.
Задача №5. Внутренняя энергия смеси газов
Условие
В закрытом сосуде находится масса m1 = 20 г азота и масса m2 = 32 г кислорода. Определить изменение ΔU внутренней энергии смеси газов при охлаждении ее на ΔТ = 28 К.
Решение
Определим количество молей азота и кислорода, а затем общее количество вещества в смеси соответственно:
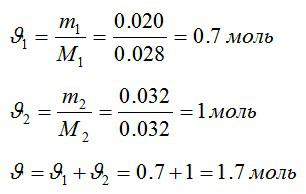
Изменение внутренней энергии:
Знак «минус» означает, что внутренняя энергия уменьшается.
Ответ: -539 Дж.
Вопросы на тему «Внутренняя энергия тела»
Вопрос 1. Что такое внутренняя энергия?
Ответ. Для начала, внутренняя энергия чего? Бутылки с пивом, воздуха в шарике, тазика с водой? Все макроскопические тела обладают энергией, заключенной внутри них: атомы твердого тела колеблются в кристаллической решетке около положений равновесия, молекулы газа находятся в постоянном хаотическом движении и т.д.
По определению:
Внутренняя энергия вещества – это энергия, которая складывается из кинетической энергии всех атомов и молекул, и потенциальной энергии их взаимодействия друг с другом.
Для идеального газа с числом степеней свободы i внутренняя энергия вычисляется по формуле:
Вопрос 2. От чего зависит внутренняя энергия идеального газа?
Ответ. Эта величина не зависит от объёма и определяется только температурой.
Вопрос 3. Как изменяется внутренняя энергия тела?
Ответ. Если тело совершает работу, его внутренняя энергия уменьшается. Например, газ передвигает поршень. Если же работа совершается над телом, то внутренняя энергия увеличивается.
Вопрос 4. Что такое функция состояния?
Ответ. Функция состояния – это один из параметров, которым можно описать термодинамическую систему. Функция состояния не зависит от того, как система пришла в то или иное состояние, а определяется несколькими переменными состояния.
Внутренняя энергия – это функция состояния термодинамической системы. В общем случае она зависит от температуры и объёма.
Вопрос 5. Можно ли изменить внутреннюю энергию тела, не совершая над ним работы?
Ответ. Да, еще один способ изменения внутренней энергии – теплопередача. В процессе теплопередачи внутренняя энергия тел изменяется.
Нужна помощь в решении задач по любой теме и других студенческих заданий? Профессиональный студенческий сервис поспособствует в выполнении работы вне зависимости от ее сложности.
Источник
