Внутренняя энергия идеального газа при закрытом сосуде
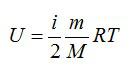
Автор Маргарита Малиновская На чтение 7 мин. Опубликовано 06.04.2020
Для понимания процессов, протекающих в природе, для их математического описания в физике используют различные упрощенные модели. Одной из них является идеальный газ. Формула внутренней энергии для него играет важную роль при изучении переходов между макроскопическими состояниями, в которых изменяются давление, объем и температура.
Идеальные газы
Прежде чем узнать, по какой формуле рассчитывается внутренняя энергия газа, следует подробно разобраться с этим классом веществ. В 1648 году ученый из Голландии Ян Баптиста ван Гельмонт ввел в физику термин «газ», который произошел от древнегреческого слова kaos (беспорядок).

Впоследствии его начали применять для всех веществ, которые соответствуют этому агрегатному состоянию. Газами стали считать любые соединения, которые проявляют следующие физические характеристики:
- не сохраняют объем, то есть занимают любое предоставленное им пространство;
- не имеют определенной формы, она зависит от сосуда, в котором находится вещество.
Газы легко сжимаемы, не имеют упругости, часто являются бесцветными, обладают низкой плотностью, легко смешиваются друг с другом в произвольных долях. Ярким примером такой смеси является воздух, состоящий из кислорода и азота, а также из многих других соединений (паров воды, углекислоты, аргона и т. д. ).
Молекулярно-кинетическая теория
Эта теория является удобным и довольно точным упрощением или моделью, которая служит для наглядного понимания процессов, происходящих в газах. Основными постулатами ее являются следующие:

- Газовые частицы движутся хаотически по прямым траекториям.
- Они не взаимодействуют друг с другом с помощью каких-либо сил, кроме механических столкновений.
- В процессе соударений кинетическая энергия системы не изменяется, то есть столкновения носят исключительно упругий характер.
- Благодаря соударениям частиц со стенками сосуда газ оказывает на них давление.
- Кинетическая энергия является единственной энергетической составляющей газа, которая однозначно определяет его абсолютную температуру.
Эти принципы легли в основу модели идеального газа, которую с успехом применяют в настоящее время для решения многих практических задач.
Она дает хорошие результаты для инертных газов при относительно высоких температурах и низких давлениях.
Общее уравнение и частные законы
Идеальный газ – это упрощенная термодинамическая модель, которая полностью базируется на принципах молекулярно-кинетической теории. Состояние любого газообразного соединения можно описать, если знать три макроскопические величины:
- давление P;
- объем V;
- температуру T.
Впервые взаимосвязь между ними нашел французский ученый Эмиль Клапейрон в 1834 году. В своих научных трудах он использовал многие работы XVII-XVIII вв. Клапейрон показал, что для любых химических соединений, которые подчиняются приближению идеальной модели газа, справедливо равенство P*V = n*R*T, где:
- n – количество вещества в молях,
- R – газовая универсальная постоянная, равная 8,31 Дж/(моль*К).
Это равенство получило название общего уравнения или выражения Клапейрона. В общем случае оно содержит 4 переменные величины (P, V, T и n).

Записанное выражение было получено Клапейроном в результате обобщения уже открытых для газов частных законов. В таблице они кратко перечисляются.
| Фамилия открывшего ученого | Постоянная величина | Формула | Кривая перехода между состояниями |
| Бойль и Мариотт | T, n | P1*V1 = P2*V2 | изотерма |
| Шарль и Гей-Люссак | P, n | V1/T1 = V2/T2 | изобара |
| Гей-Люссак | V, n | P1/T1 = P2/T2 | изохора |
| Авогадро | P, T | V1/n1 = V2/n2 | изобарно-изотермический переход |
Каждый из законов легко может получить любой школьник, если обратится к общему уравнению. Например, если взять газ в закрытом сосуде, имеющем объем V, то выражение Клапейрона запишется так: P1*V = n*R*T1. Здесь индекс 1 показывает начальное состояние системы.
Теперь можно нагреть систему до некоторой температуры T2. Поскольку сосуд является закрытым, то объем во время его нагрева не изменяется, также остается постоянным количество частиц газа n. Уравнение Клапейрона для нового состояния системы принимает вид P2*V = n*R*T2. Оба выражения следует преобразовать таким образом, чтобы переменные находились в одной стороне равенства, а постоянные – в другой:
- P1/T1 = n*R/V;
- P2/T2 = n*R/V.
Приравнивая левые части равенств, можно получить формулу закона Гей-Люссака.
Внутренняя энергия

Любая система частиц с точки зрения термодинамики запасает в себе определенную внутреннюю (потенциальную) энергию. Теоретически она может быть использована для осуществления полезной работы. Единицей энергии в СИ является джоуль (Дж). Иногда в задачах могут встречаться расчеты в калориях, но они легко переводятся в единицы системы СИ (1 калория = 4,184 Дж).
Первый постулат термодинамики
Пусть существует некоторая газовая система, которая находится в состоянии 1. Под ним понимают набор термодинамических величин, характеризующих его однозначно. В случае перехода в состояние 2 энергетическое уравнение процесса запишется в следующей форме: Q (1−2) = A (1−2) + U (1−2).
Здесь Q (1−2) будет называться энергией, которая поглощена или выделена системой в процессе изменения ее состояния из 1 в 2. Эта величина в большинстве случаев указывает на энергетический (тепловой) обмен. Величина A (1−2) показывает механическую работу, совершенную газом в рассматриваемом процессе. Слагаемое, которое обозначается U (1−2), – это изменение внутренней энергии, запасенной газом.
Записанное равенство носит название первого закона термодинамики. Оно говорит о том, что энергия не появляется из ниоткуда и не исчезает бесследно, а лишь преобразуется в различные состояния.
Составляющие величины U
Если вспомнить приближения теории молекулярно-кинетической, то можно сказать, что для газа внутренняя энергия определяется исключительно его кинетической составляющей. Никакие взаимодействия между частицами с помощью энергетических полей не существуют. Кинетическая энергия является суммой следующих вкладов:
- поступательных движений частиц;
- их вращения вокруг собственных осей;
- их колебаний около некоторого внутреннего центра симметрии.
В случае одноатомного идеального газа формула для U будет включать только поступательную составляющую кинетического движения атомов, поскольку иные степени свободы у них отсутствуют.
Получение формулы

Пусть имеется система с идеальным газом, который занимает определенный сосуд. С помощью трубки присоединим этот сосуд к другому пустому, тогда газ практически мгновенно займет весь предоставленный ему объем. Поскольку процесс протекает быстро, то можно говорить, что обмен теплом с окружающей средой равен нулю (Q (1−2)=0). При этом система не совершает никакой механической работы (A (1−2)=0).
Это означает, что ее энергия U также остается неизменной: U (1−2) = 0. Так как переход является изотермическим, можно смело утверждать, что величина U – это исключительно функция температуры, а не давления или объема. Постоянство U подтверждается законом Бойля-Мариотта: P*V = n*R*T = const.
Чтобы получить формулу энергии газа, нужно выбрать произвольный процесс, который сопровождается изменением температуры, и разложить его на два перехода: изотермический (1−1′) и изохорный (1′-2). После первого из них величина U останется постоянной, после второго она изменится на следующую величину: U (1′-2) = n*Cv*(T2-T1).

Здесь T2, T1 – конечная и начальная абсолютные температуры системы, соответственно, Cv – теплоемкость при постоянном объеме. Так как U (1−1′) = 0 (изотермический переход), то можно записать следующее выражение: ΔU = n*Cv* ΔT.
Записанная формула позволяет производить расчет изменения ΔU для любых типов идеального газа. Для них будет различаться лишь само значение Cv:
- для одноатомного Cv = 3/2*R;
- для двухатомного Cv = 5/2*R;
- для трехатомного и более Cv = 3*R.
Теплоемкость при постоянном давлении
Любой неизотермический переход между двумя газовыми состояниями можно представить не только с использованием изохоры, но и через изобару. В этом случае первый закон термодинамики запишется в следующем виде: Q = A + ΔU. При изобарном переходе газ совершает механическую работу, которая вычисляется так: A = P* ΔV = n*R* ΔT.
Согласно определению при охлаждении на 1 К системы, состоящей из 1 моля частиц газа без изменения давления, выделяется энергия Cp (теплоемкость при постоянной величине P). Тогда получается для изобарного перехода следующая формула: Q = n*Cp* ΔT.
Подставляя все выражения для A, Q и ΔU в формулу первого постулата термодинамики, можно получить следующее равенство: n*Cp* ΔT = n*R* ΔT + n*Cv* ΔT =>Cp = R + Cv.
Эта формула связывает две разные теплоемкости друг с другом, что позволяет использовать любую из них для расчета изменения внутренней энергии ΔU.
Таким образом, модель идеального газа является универсальным теоретическим инструментом для исследования изменения макроскопических термодинамических величин давления, температуры и объема. С ее помощью легко получить и использовать формулу для расчета изменения внутренней энергии газовой системы, которая зависит исключительно от температуры и определяется только кинетическим вкладом составляющих молекул.
Источник
Решение задач – занятие, которое любит далеко не каждый. Здесь мы стараемся сделать так, чтобы оно занимало у вас поменьше времени без ущерба для качества самого решения. Тема этой статьи – задачи на внутреннюю энергию.
Подписывайтесь на наш телеграм и читайте полезные материалы для студентов каждый день!
Решение задач: внутренняя энергия
Прежде чем приступать к задачам на внутреннюю энергию тела, посмотрите общую памятку по решению физических задач. И пусть под рукой на всякий случай всегда будут основные физические формулы.
Задача №1. Изменение внутренней энергии
Условие
Воздушный шар объёмом 500 м3 наполнен гелием под давлением 105 Па. В результате нагрева температура газа в аэростате поднялась от 10 °С до 25 °С. Как увеличилась внутренняя энергия газа?
Решение
Для решения будем использовать формулу внутренней энергии идеального газа:
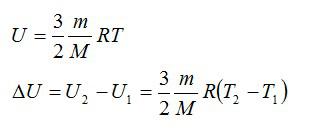
Массу гелия выразим из уравнения Клапейрона-Менделеева:
Тогда можно записать:
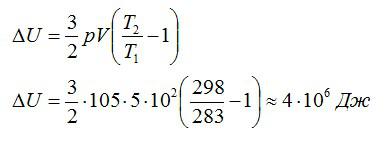
Ответ: 4 МДж.
Задача №2. Внутренняя энергия и работа
Условие
Азот массой 200 г расширяется изотермически при температуре 280 К, причем объём газа увеличивается в 2 раза. Найти:
- Изменение ∆U внутренней энергии газа.
- Совершенную при расширении газа работу А.
- Количество теплоты Q, полученное газом.
Решение
Так как процесс изотермический, то изменение внутренней энергии равно нулю, а работа равна количеству теплоты, полученному газом:
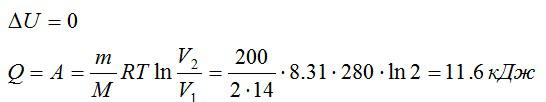
Ответ: 0; 11,6 кДж; 11,6 кДж.
Задача №3. Изменение внутренней энергии при изобарном и изохорном процессе
Условие
Кислород занимает объём V1= 3 л при давлении p1= 820 кПа. В результате изохорного нагревания и изобарного расширения газ переведён в состояние с объёмом V2= 4,5 л и давлением p2= 600 кПа. Найти количество теплоты, полученное газом; изменение внутренней энергии газа.
Решение
Теплота, подведенная к газу, идет на совершение работы и изменение внутренней энергии:
В изохорном и изобарном процессе соответственно:
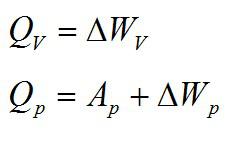
Изохорное нагревание:
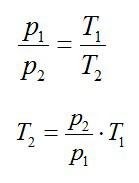
Изменение внутренней энергии при изохорном процессе:
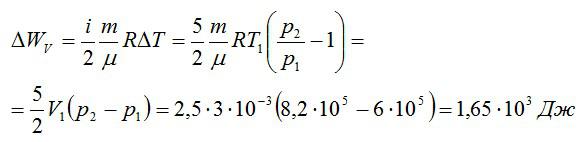
Изменение внутренней энергии при изобарном процессе:
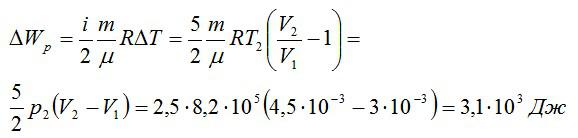
Общее изменение внутренней энергии:
Ответ: 4,75 кДж.
Задача №4. Изменение внутренней энергии двухатомного газа
Условие
Кислород массой 2 кг занимает объём 6 м3 и находится под давлением 1 атм. Газ был нагрет сначала при постоянном давлении до объёма 13 м3, а затем при постоянном объёме – до давления 23 атм. Найти изменение внутренней энергии газа.
Решение
Изменение внутренней энергии находим по формуле:
Эту форму можно преобразовать, используя уравнение Клапейрона-Менделеева:
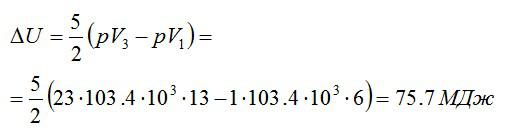
Ответ: 75,7 МДж.
Задача №5. Внутренняя энергия смеси газов
Условие
В закрытом сосуде находится масса m1 = 20 г азота и масса m2 = 32 г кислорода. Определить изменение ΔU внутренней энергии смеси газов при охлаждении ее на ΔТ = 28 К.
Решение
Определим количество молей азота и кислорода, а затем общее количество вещества в смеси соответственно:
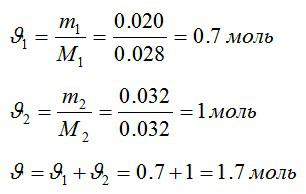
Изменение внутренней энергии:
Знак «минус» означает, что внутренняя энергия уменьшается.
Ответ: -539 Дж.
Вопросы на тему «Внутренняя энергия тела»
Вопрос 1. Что такое внутренняя энергия?
Ответ. Для начала, внутренняя энергия чего? Бутылки с пивом, воздуха в шарике, тазика с водой? Все макроскопические тела обладают энергией, заключенной внутри них: атомы твердого тела колеблются в кристаллической решетке около положений равновесия, молекулы газа находятся в постоянном хаотическом движении и т.д.
По определению:
Внутренняя энергия вещества – это энергия, которая складывается из кинетической энергии всех атомов и молекул, и потенциальной энергии их взаимодействия друг с другом.
Для идеального газа с числом степеней свободы i внутренняя энергия вычисляется по формуле:
Вопрос 2. От чего зависит внутренняя энергия идеального газа?
Ответ. Эта величина не зависит от объёма и определяется только температурой.
Вопрос 3. Как изменяется внутренняя энергия тела?
Ответ. Если тело совершает работу, его внутренняя энергия уменьшается. Например, газ передвигает поршень. Если же работа совершается над телом, то внутренняя энергия увеличивается.
Вопрос 4. Что такое функция состояния?
Ответ. Функция состояния – это один из параметров, которым можно описать термодинамическую систему. Функция состояния не зависит от того, как система пришла в то или иное состояние, а определяется несколькими переменными состояния.
Внутренняя энергия – это функция состояния термодинамической системы. В общем случае она зависит от температуры и объёма.
Вопрос 5. Можно ли изменить внутреннюю энергию тела, не совершая над ним работы?
Ответ. Да, еще один способ изменения внутренней энергии – теплопередача. В процессе теплопередачи внутренняя энергия тел изменяется.
Нужна помощь в решении задач по любой теме и других студенческих заданий? Профессиональный студенческий сервис поспособствует в выполнении работы вне зависимости от ее сложности.
Источник
