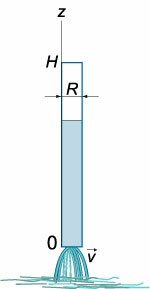
Вода через небольшое отверстие в дне сосуда вытекает за время t
Закон Торричелли
Итальянский ученый Эванджелиста Торричелли, изучавший движение жидкостей,
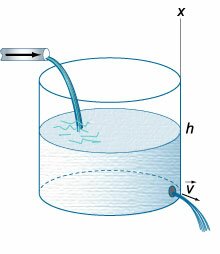
в (1643) году экспериментально обнаружил, что скорость вытекания жидкости через малое отверстие на дне открытого сосуда (рисунок (1)) описывается формулой:
[v = sqrt {2gh} ,]
где (h) − высота уровня жидкости над отверстием, (g) − гравитационная постоянная.
| |
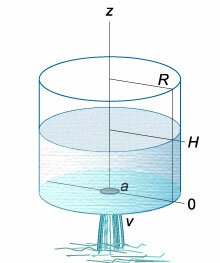
Рис.1 | Рис.2 |
Такая же формула описывает скорость тела, свободного падающего с высоты (h) в поле тяжести Земли в вакууме.
В действительности, найденная формула не совсем точна. В более точном приближении скорость жидкости зависит от формы и размера отверстия, от вязкости жидкости и режима течения. Поэтому,
формула Торричелли часто записывается с дополнительным множителем (varphi:)
[v = varphisqrt {2gh} ,]
где коэффициент (varphi) близок к (1.) Значения параметра (varphi) для отверстий различной формы и размера можно найти в гидравлических справочниках.
Вытекание жидкости из тонкой трубки
Вытекание жидкости из тонкой длинной трубки (рисунок (2)) имеет ряд особенностей. Здесь важную роль играют капиллярные эффекты, обусловленные
поверхностным натяжением и смачиванием вследствие контакта со стенками трубки.
Скорость вытекания жидкости из капиллярных трубок приблизительно пропорциональна высоте столба жидкости над отверстием, то есть
[v = kh,]
где (k) − некоторая константа, зависящая от вязкости жидкости, геометрии и материала трубки.
Далее мы будем описывать вытекание жидкости с помощью дифференциальных уравнений из сосудов обоих типов (широкого и тонкого).
Дифференциальное уравнение вытекания жидкости
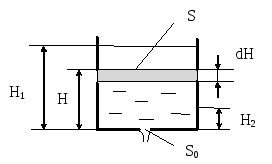
Данное дифференциальное уравнение можно вывести, рассматривая баланс жидкости в сосуде. Возьмем, например, цилиндрический сосуд с широким основанием, радиус
которого равен (R.) Предположим, что жидкость вытекает через малое отверстие радиуса (a) на дне сосуда (рисунок (3)).
|
|
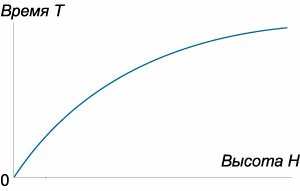
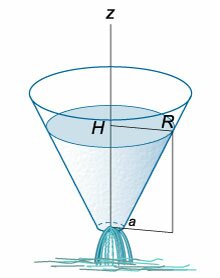
Рис.3 | Рис.4 |
Скорость жидкости описывается формулой Торричелли:
[v = sqrt {2gz} ,]
где (z) − высота жидкости над отверстием. Тогда поток жидкости определяется выражением:
[q = – pi {a^2}sqrt {2gz} .]
Здесь (pi {a^2}) соответствует площади отверстия, через которое вытекает жидкость, а знак “минус” означает,
что уровень жидкости уменьшается по мере ее вытекания из резервуара.
Уравнение баланса жидкости в резервуаре описывается следующим образом:
[frac{{dV}}{{dt}} = q.]
Поскольку изменение объема (dV) можно выразить как
[dV = Sleft( z right)dz,]
то мы получаем дифференциальное уравнение
[frac{{Sleft( z right)dz}}{{dt}} = qleft( z right).]
Подставим функцию (qleft( z right)) в это уравнение:
[frac{{Sleft( z right)dz}}{{dt}} = – pi {a^2}sqrt {2gz} .]
Поперечное сечение ({Sleft( z right)}) цилиндрического сосуда не зависит от высоты (z) и равно
[Sleft( z right) = pi {R^2},]
где (R) − радиус основания цилиндра. Тогда
[require{cancel}
cancel{pi} {R^2}frac{{dz}}{{dt}} = – cancel{pi} {a^2}sqrt {2gz} .
]
В результате получаем уравнение с разделяющимися переменными:
[frac{{dz}}{{sqrt z }} = – frac{{{a^2}}}{{{R^2}}}sqrt {2g} dt.]
Теперь проинтегрируем полученное уравнение, считая, что начальный уровень жидкости составляет (H,) и за время (T) он уменьшается до (0:)
[
{intlimits_H^0 {frac{{dz}}{{sqrt z }}} = – intlimits_0^T {frac{{{a^2}}}{{{R^2}}}sqrt {2g} dt} ,};;
{Rightarrow 2left[ {left. {left( {sqrt z } right)} right|_H^0} right] = – frac{{{a^2}}}{{{R^2}}}sqrt {2g} left[ {left. {left( t right)} right|_0^T} right],};;
{Rightarrow 2sqrt H = frac{{{a^2}}}{{{R^2}}}sqrt {2g} T,};;
{Rightarrow sqrt {2H} = frac{{{a^2}}}{{{R^2}}}sqrt g T.}
]
Отсюда следует выражение для полного времени вытекания жидкости (T:)
[T = frac{{{R^2}}}{{{a^2}}}sqrt {frac{{2H}}{g}} .]
Интересно, что в предельном случае (a = R) (когда площади отверстия и самого цилиндра равны), полученная
формула преобразуется в известную формулу (T = sqrt {largefrac{{2H}}{g}normalsize}, )
которая определяет время падения материального тела с высоты (H.) Зависимость времени (T) от высоты (H) схематически показана на рисунке (4.)
Аналогично можно описать вытекание жидкости и из сосуда другой формы.
Вывести дифференциальное уравнение вытекания жидкости из конического сосуда и определить полное время вытекания (T.)
Радиус верхнего основания конического сосуда равен (R,) а радиус нижнего основания (a.) Начальная уровень жидкости составляет (H) (рисунок (5)).
| |
Рис.5 | Рис.6 |
Изменение уровня жидкости на высоте (z) описывается дифференциальным уравнением
[Sleft( z right)frac{{dz}}{{dt}} = qleft( z right),]
где (Sleft( z right)) − площадь поперечного сечения сосуда на высоте (z,) а (qleft( z right)) − поток жидкости, зависящий от высоты (z.)
Принимая во внимание геометрию сосуда, можно предположить, что закон Торричелли выполняется. Поэтому, можно записать:
[qleft( z right) = – pi {a^2}sqrt {2gz} ,]
где (a) − радиус отверстия на дне конического сосуда. Учитывая, что отверстие достаточно малое, осевое сечение можно рассматривать как треугольник
(рисунок (6) выше). Из подобия треугольников следует, что
[frac{R}{H} = frac{r}{z}.]
Следовательно, площадь поверхности жидкости на высоте (z) будет равна
[
{Sleft( z right) = pi {r^2} }
= {pi {left( {frac{{Rz}}{H}} right)^2} }
= {frac{{pi {R^2}{z^2}}}{{{H^2}}}.}
]
Подставляя (Sleft( z right)) и (qleft( z right)) в дифференциальное уравнение, имеем:
[frac{{pi {R^2}{z^2}}}{{{H^2}}}frac{{dz}}{{dt}} = – pi {a^2}sqrt {2gz} .]
После простых преобразований получаем следующее дифференциальное уравнение:
[{z^{largefrac{3}{2}normalsize}}dz = – frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} dt.]
Проинтегрируем обе части, учитывая, что уровень жидкости уменьшается от начального значения (H) до нуля за время (T:)
[
{intlimits_H^0 {{z^{largefrac{3}{2}normalsize}}dz} = – intlimits_0^T {frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} dt} ,};;
{Rightarrow left. {left( {frac{{{z^{largefrac{5}{2}normalsize}}}}{{frac{5}{2}}}} right)} right|_0^H = frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} left[ {left. {left( t right)} right|_0^T} right],};;
{Rightarrow frac{2}{5}{H^{largefrac{5}{2}normalsize}} = frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} T,};;
{Rightarrow frac{1}{5}sqrt {frac{{2H}}{g}} = frac{{{a^2}}}{{{R^2}}}T,};;
{Rightarrow T = frac{{{R^2}}}{{5{a^2}}}sqrt {frac{{2H}}{g}} .}
]
Здесь мы снова видим аналогию с падением материального тела с высоты (H) в гравитационном поле Земли. Как известно,
время падения описывается формулой:
[T = sqrt {frac{{2H}}{g}}. ]
Если мы сравним этот результат со случаем вытекания жидкости из цилиндрического сосуда, то видно, что при тех же самых
значениях (H, R) и (a) время вытекания жидкости из конического сосуда ровно в (5) раз меньше, чем из цилиндра (хотя
объем конического сосуда меньше лишь в (3) раза!). Такие целочисленные отношения в природе выглядят удивительными, не правда ли?
Исследовать вытекание жидкости из тонкой трубки радиусом (R) и высотой (H,) считая трубку полностью заполненной жидкостью.
|
|
Рис.7 | Рис.8 |
Аналогично разобранным выше примерам, мы можем записать уравнение баланса жидкости на некоторой произвольной высоте (z) в следующей форме:
[Sleft( z right)frac{{dz}}{{dt}} = qleft( z right).]
В данном случае площадь поперечного сечения (Sleft( z right)) является константой:
[Sleft( z right) = S = pi {R^2},]
и поток жидкости, вытекающей из сосуда, определяется формулой:
[qleft( z right) = – kz,]
где (k) зависит от размера отверстия, смачиваемости и других параметров.
В результате получаем простое дифференциальное уравнение:
[pi {R^2}frac{{dz}}{{dt}} = – kz,]
или после разделения переменных:
[frac{{dz}}{z} = – frac{k}{{pi {R^2}}}dt.]
Теперь это уравнение можно проинтегрировать, считая, что уровень жидкости уменьшается с высоты (H) до (h) за время от (0) до (t:)
[
{intlimits_H^h {frac{{dz}}{z}} = – intlimits_0^t {frac{k}{{pi {R^2}}}dt} ,};;
{Rightarrow left. {left( {ln z} right)} right|_h^H = frac{k}{{pi {R^2}}}t,};;
{Rightarrow t = frac{{pi {R^2}}}{k}left( {ln H – ln h} right) = frac{{pi {R^2}}}{k}ln frac{H}{h}.}
]
Зависимость времени (t) от отношения (largefrac{H}{h}normalsize) показана схематически на рисунке (8.)
Данная кривая аналогична зависимости времени (T) от высоты (H) для широкого цилиндрического сосуда, для которого справедлив закон Торричелли.
Интересно, что в данной простой модели время вытекания жидкости (t) формально стремится к бесконечности при (h to 0.)
Источник
Решебник
ВСЕ
ФИЗИКА
МАТЕМАТИКА
ХИМИЯ
Задача по физике – 1448
Из крана выливается вода. Начиная с некоторого места диаметр струи уменьшается на протяжении $h$ от $b$ до $c$.
Сколько воды вытечет из крана за время $t$?
Подробнее
Задача по физике – 1449
Из широкого сосуда через узкую цилиндрическую трубку вытекает жидкость плотности $rho$. Как распределены по вертикали давление и скорость жидкости в сосуде и трубке? Давление воздуха $P_{0}$.
Подробнее
Задача по физике – 1450
Сосуд с водой подвешен к потолку. Высота воды в сосуде $H$. На сколько изменится натяжение веревки, если в днище сосуда открыть маленькое отверстие сечения $S$, из которого вытекает вода?
Подробнее
Задача по физике – 1451
Из отверстия в дне высокого сосуда вытекает вода. Сечение сосуда $S_{1}$, сечение струи $S_{2}$. Уровень воды в сосуде перемещается с постоянным ускорением. Найдите это ускорение.
Подробнее
Задача по физике – 1452
Насос должен подавать ежесекундно объем воды $Q$ на высоту $H$ по трубе постоянного сечения $S$. Какова должна быть мощность насоса? КПД насоса $eta$, плотность воды $rho$.
Подробнее
Задача по физике – 1453
По трубе сечением $S$, изогнутой под прямым углом, течет вода со скоростью $v$. Плотность воды $rho$.
Чему равна сила бокового давления в месте закругления трубы?
Подробнее
Задача по физике – 1821
Как вы думаете, справедлив ли закон сообщающихся Сосудов (однородная жидкость в сообщающихся сосудах имеет один и тот же уровень), если в одном из сосудов на поверхности жидкости находится некоторый поплавок (капиллярность не учитывать)?
Подробнее
Задача по физике – 1822
Достаточно длинная открытая снизу трубка с плотно пригнанным поршнем, который может все же двигаться по трубке без трения, находится под водой и удерживается с помощью веревки (рис.). Верхний конец трубки над поршнем пустой. Как зависит сила натяжения веревки от глубины погружения трубки в воду?

Подробнее
Задача по физике – 1823
Ведро, имеющее массу $m$, вместимость $V$, вытаскивают с водой из колодца. Плотность материала, из которого сделано ведро, равна $rho$, плотность воды $rho_{в}$. Какую силу необходимо приложить для подъема этого ведра, пока оно находится под водой и когда его вытащили из воды? Сопротивление воды движению ведра не учитывать.
Подробнее
Задача по физике – 1824
Для того чтобы поднять уровень жидкости в сосуде на Высоту $h$ с помощью насоса, надо совершить некоторую работу. Изменится ли необходимая для этой же цели работа, если на поверхности жидкости плавает какое-нибудь тело?
Подробнее
Задача по физике – 1825
Изменится ли осадка парохода, перешедшего из северных вод в экваториальные, вследствие изменения ускорения свободного падения с широтой?
Подробнее
Задача по физике – 1826
Как зависит подъемная сила аэростата от температуры, при которой производится его подъем?
Подробнее
Задача по физике – 1827
Когда объясняют опыт со взвешиванием воздуха, [иногда говорят, что сначала взвешивают колбу с воздухом, а затем, после откачки воздуха из колбы, взвешивают одну колбу. Разность показаний весов в первом и втором случаях и составляет массу воздуха в объеме колбы. Правильно ли такое толкование опыта по взвешиванию воздуха?
Подробнее
Задача по физике – 1828
Можно ли измерить плотность воздуха, взвешивая мягкий воздухонепроницаемый мешок сначала пустой (сжатый), а потом наполненный воздухом? Объем мешка в наполненном Состоянии известен.
Подробнее
Источник
4.1. Найти скорость v течения углекислого газа по трубе, если известно, что за время t= 30 мин через поперечное сечение трубы протекает масса газа m = 0,51 кг. Плотность газа р = 7,5 кг/м3. Диаметр трубы D= 2 см.
Решение:
4.2. В дне цилиндрического сосуда диаметром D= 0,5 м име круглое отверстие диаметром d= 1см. Найти зависимость скорости понижения уровня воды в сосуде от высоты hэтого уровня. Найти значение этой скорости для высоты h= 0,2 м.
Решение:
4.3. На столе стоит сосуд с водой, в боковой поверхности которого имеется малое отверстие, расположенное на рас h1 от дна сосуда и на расстоянии h2от уровня воды. Уровень воды в сосуде поддерживается постоянным. На каком расстоянии l от сосуда ( по горизонтали) струя воды падает на стол в случае, если: a) h1= 25 см, h2=16см ; б) h1 =16 см, h2 = 25 см?
Решение:
4.4. Сосуд, наполненный водой, сообщается с атмосферой через стеклянную трубку, закрепленную в горлышке сосуда. Кран К находится на расстоянии h2= 2 см от дна сосуда. Найти скорость v вытекания воды из крана в случае, если расстояние между нижним концом трубки и дном сосуда: а) h1 = 2 см; б) h1 =7,5 см; в) h1 =10 см.
Решение:
4.5. Цилиндрической бак высотой h= 1 м наполнен до краев водой. За какое время t вся вода выльется через отверстие, расположенное у дна бака, если площадь S2поперечного сечения отверстия в 400 раз меньше площади поперечного сечения бака? Сравнить это время с тем, которое понадобилось бы для вытекания того же объема воды, если бы уровень воды в баке поддерживался постоянным на высоте h= 1 м от отверстия.
Решение:
4.6. В сосуд льется вода, причем за единицу времени наливается объем воды V1= 0,2 л/с. Каким должен быть диаметр dотверстия в дне сосуда, чтобы вода в нем держалась на постоянном уровне h =8,3 см?
Решение:
4.7. Какое давление р создает компрессор в краскопульте, если струя жидкой краски вылетает из него со скоростью v = 25 м/с? Плотность краски р = 0,8 • 103 кг/м3.
Решение:
4.8. По горизонтальный трубе АВ течет жидкость. Разность уровней этой жидкости в трубах а и bравна dh = 10 см. Диаметры трубок а и bодинаковы. Найти скорость v течения жидкости в трубе АВ.
Решение:
4.9. Воздух продувается через трубку АВ. За единицу времени через трубку АВ протекает объем воздуха V1= 5 л/мин. Площадь поперечного сечения широкой части трубки АВ равна S1 = 2 см2, а узкой ее части и трубки abcравна S2= 0,5 см2. Найти разность уровней dhводы, налитой в трубку abc. Плотность воздуха р = 1,32 кг/м3.
Решение:
4.10. Шарик всплывает с постоянной скоростью v в жид, плотность р1которой в 4 раза больше плоскости мате шарика. Во сколько раз сила трения Fтр , действующая на всплывающий шарик, больше силы тяжести mg, действующей на этот шарик?
Решение:
4.11. Какой наибольшей скорости v может достичь дождевая капля диаметром d= 0,3 мм, если динамическая вязкость воз n= 1,2-10-5 Па*с?
Решение:
4.12. Стальной шарик диаметром d = 1мм падает с посто скоростью v = 0,185 см/с в большом сосуде, наполненном касторовым маслом. Найти динамическую вязкость nкасторо масла.
Решение:
4.13. Смесь свинцовых дробинок с диаметрами d1 =3 мм и d2= 1 мм опустили в бак с глицерином высотой h= 1 м. На сколько позже упадут на дно дробинки меньшего диаметра по сравнению с дробинками большего диаметра? Динамическая вязкость глицерина n= 1,47 Па*с.
Решение:
4.14. Пробковый шарик радиусом r = 5 мм всплывает в сосуде, наполненном касторовым маслом. Найти динамическую и кинематическую вязкости касторового масла, если шарик всплывает с постоянной скоростью v = 3,5 см/с.
Решение:
4.15. В боковую поверхность цилиндрического сосуда радиусом R = 2 см вставлен горизонтальный капилляр, внутренний радиус r= 1 мм которого и длина l = 2 см. В сосуд налито касторовое масло, динамическая вязкость которого n= 1,2Па*с. Найти зависимость скорости v понижения уровня касторового масла в сосуде от высоты hэтого уровня над капилляром. Найти значение этой скорости при h= 26 см.
Решение:
4.16. В боковую поверхность сосуда вставлен горизон капилляр, внутренний радиус которого r= 1 мм и длина l = 1,5 см. В сосуд налит глицерин, динамическая вязкость которого n= 1,0Па*с. Уровень глицерина в сосуде поддержи постоянным на высоте h = 0,18м выше капилляра. Какое время потребуется на то, чтобы из капилляра вытек объем глицерина V = 5 см3?
Решение:
4.17. На столе стоит сосуд, в боковую поверхность которого вставлен горизонтальный капилляр на высоте h1= 5 см от дна сосуда. Внутренний радиус капилляра r =1 мм и длина l = 1 см. В сосуд налито машинное масло, плотность которого р = 0,9 • 103 кг/м3 и динамическая вязкость n = 0,5 Па*с. Уровень масла в сосуде поддерживается постоянным на высоте h2– 50 см выше капилляра. На каком расстоянии Lот конца капилляра (по горизонтали) струя масла падает на стол?
Решение:
4.18. Стальной шарик падает в широком сосуде, напол трансформаторным маслом, плотность которого р — 0,9 • 103 кг/ m3 и динамическая вязкость n= 0,8Па*с. Считая, что закон Стокса имеет место при числе Рейнольдса Re< 0,5 (если при вычислении Reв качестве величины Dвзять диаметр шарика), найти предельное значение диаметра Dшарика.
Решение:
4.19. Считая, что ламинарность движения жидкости (или газа) в цилиндрической трубе сохраняется при числе Рейнольдса Rе<3000 (если при вычислении Reв качестве величины Dвзять диаметр трубы), показать, что условия задачи 4.1 соответствуют ламинарному движению. Кинематическая вязкость газа v = 1,33 • 10-6 м2/с.
Решение:
4.20. Вода течет по трубе, причем за единицу времени через поперечное сечение трубы протекает объем воды V1= 200см3/с. Динамическая вязкость воды n =0,001 Па*с. При каком предельном значении диаметра Dтрубы движение воды остается ламинарным? (Смотри условие предыдущей задачи.)
Решение:
/>
Источник
Знать,
чтобы предвидеть,
предвидеть,
чтобы обладать властью.
А.Шопенгауэр
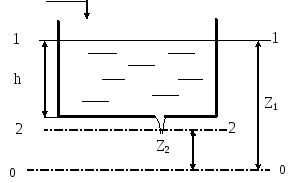
Пусть
имеем гидравлическую схему течения
жидкости, представленную на рис. 1.4 а.
Уровень жидкости поддерживается
постоянным за счет постоянной подпитки
сверху, объемным расходом V.
Жидкость имеет малую вязкость, и силы
инерции доминируют над силами вязкого
трения.
а
б
Рис.
1.4. Истечение жидкости из сосуда: а –
при постоянном уровне; б – при переменном
уровне.
Высота
уровня жидкости h.
Составим уравнение Бернулли для двух
сечений – поверхности жидкости и струи
(1-1 и 2-2)
![]() .
.
Согласно
уравнению потенциальная энергия
положения жидкости (высотой h)
превращается в кинетическую энергию
струи. Так как уровень поверхности
поддерживается постоянным, то скорость
на поверхности жидкости нулевая (0
=0), а скорость истечения определяется
соотношением
![]() ,
,
кроме
того, z1=0,
z0=h.
Пусть давление над поверхностью жидкости
равно давлению на выходе из сосуда Р0=Р1
–т.е. сосуд открытый. Тогда получим
формулу Торричелли для идеальной
жидкости:
![]() .
.
Скорость истечения не зависит от диаметра
отверстия, а определяется лишь высотой
уровня жидкости в емкости. Расчетная
формула сохраняет смысл, даже если
отверстие находится на боковой стенке
сосуда.
Для реальной жидкости необходимо учесть
потери трения на входе в насадок, поэтому
необходимо ввести множитель
![]() ,
,
где
– коэффициент расхода (1):
для отверстий в стенке =0,6;
для коротких цилиндрических насадок
= 0,97.
Объемный
расход определяется произведением
скорости на площадь сечения выходного
отверстия
![]() ,
,
где
fотв
– площадь
выходного отверстия.
Поскольку
полученная формула однозначно связывает
расход жидкости с ее уровнем, то,
контролируя уровень, можно контролировать
расход жидкости. Это свойство используется
для измерения расхода.
Пример.
Найти
расход воды, вытекающей из емкости, если
уровень жидкости h=2м,
диаметр отверстия d=2
см., коэффициент расхода α=0,97.
Решение.
Используем
расчетную формулу
![]() .
.
Сечение отверстия
![]() .
.
Подставив в формулу
численные значения, получим
.
Задачи.
1.
Найти диаметр сливного отверстия в
емкости, если расход жидкости V=5*10-4
м/с, высота уровня жидкости h=1
м, коэффициент расхода 0,6.
2. Как изменится
уровень жидкости, если расход увеличить
в два раза?
1.3. Истечение при переменном уровне
Число является
универсальным ключом, одновременно
открывающим доступ к истине и красоте.
Лука Пачоли.
Требуется
определить продолжительность слива
жидкости от уровня h1
до h2
(см. Рис.
1.4 б). Сосуд был предварительно заполнен
и приток жидкости сверху отсутствует.
Поскольку уровень жидкости непрерывно
меняется, то скорость истечения будет
изменяться: наибольшая в начале слива
и наименьшая – в конце.
Выделим
в жидкости участок толщиной dh.
Составим уравнение расхода для выделенного
участка. Его элементарный объем -dh*F.
С другой стороны, объём вытекающей
жидкости за время
![]() d
d
составляет
![]() ,
,
где
F
– площадь сечения сосуда, -
время.
Приравняв эти выражения, получим
дифференциальное уравнение первого
порядка, связывающее уровень жидкости
и время
![]() .
.
Разделим переменные и проинтегрируем
с учетом начального условия
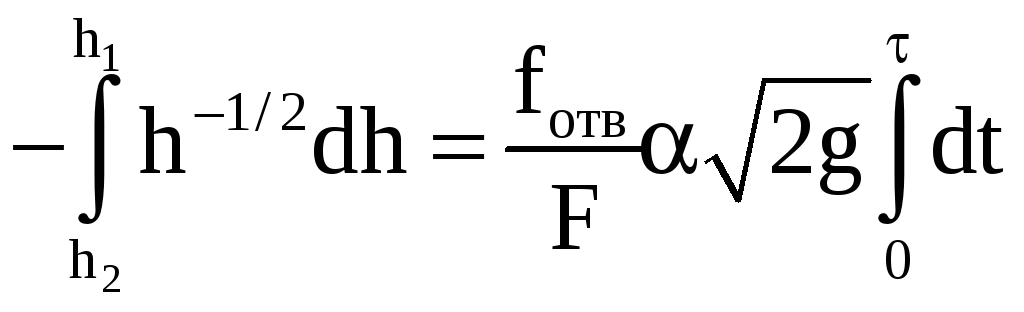 .
.
После несложных преобразований получим
выражение для расчета продолжительности
слива
![]()
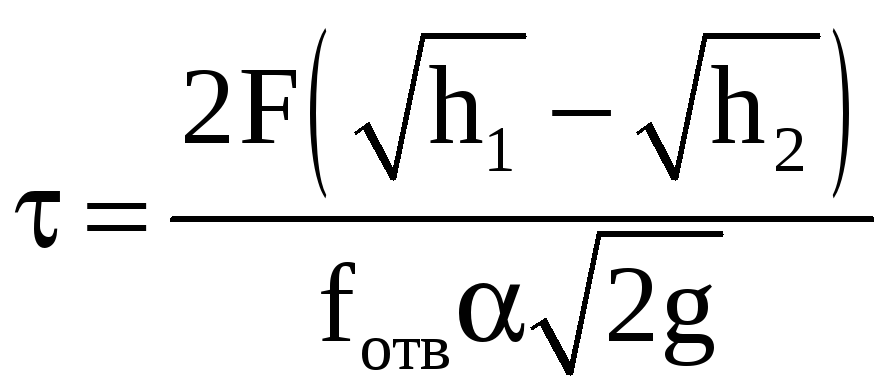 .
.
В
случае полного опорожнения сосуда
необходимо положить h2=0.
При этом расчетная формула примет вид
![]()
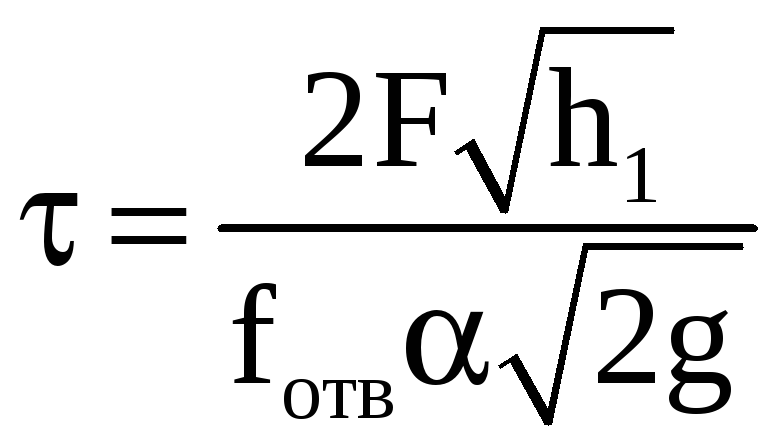 .
.
Если
сосуд имеет форму, отличную от
цилиндрической, например, коническую,
то необходимо при интегрировании
учитывать функциональную зависимость
площади поперечного сечения от высоты,
и расчетное уравнение будет иметь другой
вид.
Пример.
Сколько
времени потребуется для полного
опорожнения цилиндрического сосуда
диаметром D=1
м, если уровень жидкости h=1
м, диаметр сливного отверстия d=1
см, коэффициент расхода α=0,6?
Решение.
Используем формулу
![]()
![]() .
.
Учитывая,
что сосуд и отверстие имеют круглую
форму, расчетную формулу можно записать
следующим образом:
![]()
![]() .
.
Подставив численные
значения, найдем время полного слива
![]()
![]() .
.
Задачи.
В
бензобак вертолета попала пуля. Бак
имеет форму параллелепипеда размерами
0,3х1х0,5 м (высота h=0,5),
он заполнен бензином наполовину. Диаметр
отверстия d=9
мм. Приняв коэффициент расхода α=0,6,
найти время полного опорожнения
бензобака.Требуется
из цилиндрического сосуда изготовить
водяные часы. Диаметр сосуда 10 см.,
начальный уровень воды 0,3 м, коэффициент
расхода 0,63. Ожидаемое время полного
слива 5 минут. Найти требуемый диаметр
отверстия.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник