Вода через отверстие в дне сосуда вытекает за время

Закон Торричелли

Итальянский ученый Эванджелиста Торричелли, изучавший движение жидкостей,
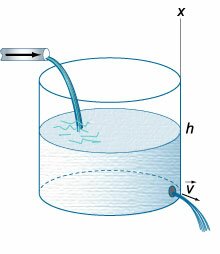
в (1643) году экспериментально обнаружил, что скорость вытекания жидкости через малое отверстие на дне открытого сосуда (рисунок (1)) описывается формулой:

[v = sqrt {2gh} ,]

где (h) − высота уровня жидкости над отверстием, (g) − гравитационная постоянная.

Такая же формула описывает скорость тела, свободного падающего с высоты (h) в поле тяжести Земли в вакууме.

В действительности, найденная формула не совсем точна. В более точном приближении скорость жидкости зависит от формы и размера отверстия, от вязкости жидкости и режима течения. Поэтому,
формула Торричелли часто записывается с дополнительным множителем (varphi:)

[v = varphisqrt {2gh} ,]

где коэффициент (varphi) близок к (1.) Значения параметра (varphi) для отверстий различной формы и размера можно найти в гидравлических справочниках.

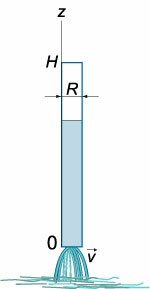
Вытекание жидкости из тонкой трубки

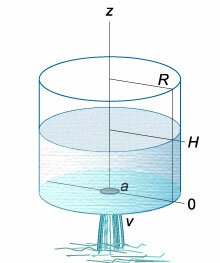
Вытекание жидкости из тонкой длинной трубки (рисунок (2)) имеет ряд особенностей. Здесь важную роль играют капиллярные эффекты, обусловленные
поверхностным натяжением и смачиванием вследствие контакта со стенками трубки.

Скорость вытекания жидкости из капиллярных трубок приблизительно пропорциональна высоте столба жидкости над отверстием, то есть

[v = kh,]

где (k) − некоторая константа, зависящая от вязкости жидкости, геометрии и материала трубки.

Далее мы будем описывать вытекание жидкости с помощью дифференциальных уравнений из сосудов обоих типов (широкого и тонкого).

Дифференциальное уравнение вытекания жидкости

Данное дифференциальное уравнение можно вывести, рассматривая баланс жидкости в сосуде. Возьмем, например, цилиндрический сосуд с широким основанием, радиус
которого равен (R.) Предположим, что жидкость вытекает через малое отверстие радиуса (a) на дне сосуда (рисунок (3)).

Скорость жидкости описывается формулой Торричелли:

[v = sqrt {2gz} ,]

где (z) − высота жидкости над отверстием. Тогда поток жидкости определяется выражением:

[q = – pi {a^2}sqrt {2gz} .]

Здесь (pi {a^2}) соответствует площади отверстия, через которое вытекает жидкость, а знак “минус” означает,
что уровень жидкости уменьшается по мере ее вытекания из резервуара.

Уравнение баланса жидкости в резервуаре описывается следующим образом:

[frac{{dV}}{{dt}} = q.]

Поскольку изменение объема (dV) можно выразить как

[dV = Sleft( z right)dz,]

то мы получаем дифференциальное уравнение

[frac{{Sleft( z right)dz}}{{dt}} = qleft( z right).]

Подставим функцию (qleft( z right)) в это уравнение:

[frac{{Sleft( z right)dz}}{{dt}} = – pi {a^2}sqrt {2gz} .]

Поперечное сечение ({Sleft( z right)}) цилиндрического сосуда не зависит от высоты (z) и равно

[Sleft( z right) = pi {R^2},]

где (R) − радиус основания цилиндра. Тогда

[require{cancel}
cancel{pi} {R^2}frac{{dz}}{{dt}} = – cancel{pi} {a^2}sqrt {2gz} .
]

В результате получаем уравнение с разделяющимися переменными:

[frac{{dz}}{{sqrt z }} = – frac{{{a^2}}}{{{R^2}}}sqrt {2g} dt.]

Теперь проинтегрируем полученное уравнение, считая, что начальный уровень жидкости составляет (H,) и за время (T) он уменьшается до (0:)

[
{intlimits_H^0 {frac{{dz}}{{sqrt z }}} = – intlimits_0^T {frac{{{a^2}}}{{{R^2}}}sqrt {2g} dt} ,};;
{Rightarrow 2left[ {left. {left( {sqrt z } right)} right|_H^0} right] = – frac{{{a^2}}}{{{R^2}}}sqrt {2g} left[ {left. {left( t right)} right|_0^T} right],};;
{Rightarrow 2sqrt H = frac{{{a^2}}}{{{R^2}}}sqrt {2g} T,};;
{Rightarrow sqrt {2H} = frac{{{a^2}}}{{{R^2}}}sqrt g T.}
]

Отсюда следует выражение для полного времени вытекания жидкости (T:)

[T = frac{{{R^2}}}{{{a^2}}}sqrt {frac{{2H}}{g}} .]

Интересно, что в предельном случае (a = R) (когда площади отверстия и самого цилиндра равны), полученная
формула преобразуется в известную формулу (T = sqrt {largefrac{{2H}}{g}normalsize}, )
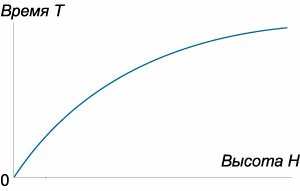
которая определяет время падения материального тела с высоты (H.) Зависимость времени (T) от высоты (H) схематически показана на рисунке (4.)

Аналогично можно описать вытекание жидкости и из сосуда другой формы.

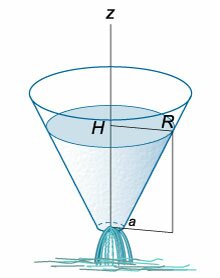
Вывести дифференциальное уравнение вытекания жидкости из конического сосуда и определить полное время вытекания (T.)
Радиус верхнего основания конического сосуда равен (R,) а радиус нижнего основания (a.) Начальная уровень жидкости составляет (H) (рисунок (5)).

Изменение уровня жидкости на высоте (z) описывается дифференциальным уравнением

[Sleft( z right)frac{{dz}}{{dt}} = qleft( z right),]

где (Sleft( z right)) − площадь поперечного сечения сосуда на высоте (z,) а (qleft( z right)) − поток жидкости, зависящий от высоты (z.)

Принимая во внимание геометрию сосуда, можно предположить, что закон Торричелли выполняется. Поэтому, можно записать:

[qleft( z right) = – pi {a^2}sqrt {2gz} ,]

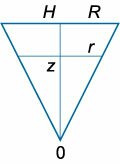
где (a) − радиус отверстия на дне конического сосуда. Учитывая, что отверстие достаточно малое, осевое сечение можно рассматривать как треугольник
(рисунок (6) выше). Из подобия треугольников следует, что

[frac{R}{H} = frac{r}{z}.]

Следовательно, площадь поверхности жидкости на высоте (z) будет равна

[
{Sleft( z right) = pi {r^2} }
= {pi {left( {frac{{Rz}}{H}} right)^2} }
= {frac{{pi {R^2}{z^2}}}{{{H^2}}}.}
]

Подставляя (Sleft( z right)) и (qleft( z right)) в дифференциальное уравнение, имеем:

[frac{{pi {R^2}{z^2}}}{{{H^2}}}frac{{dz}}{{dt}} = – pi {a^2}sqrt {2gz} .]

После простых преобразований получаем следующее дифференциальное уравнение:

[{z^{largefrac{3}{2}normalsize}}dz = – frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} dt.]

Проинтегрируем обе части, учитывая, что уровень жидкости уменьшается от начального значения (H) до нуля за время (T:)

[
{intlimits_H^0 {{z^{largefrac{3}{2}normalsize}}dz} = – intlimits_0^T {frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} dt} ,};;
{Rightarrow left. {left( {frac{{{z^{largefrac{5}{2}normalsize}}}}{{frac{5}{2}}}} right)} right|_0^H = frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} left[ {left. {left( t right)} right|_0^T} right],};;
{Rightarrow frac{2}{5}{H^{largefrac{5}{2}normalsize}} = frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} T,};;
{Rightarrow frac{1}{5}sqrt {frac{{2H}}{g}} = frac{{{a^2}}}{{{R^2}}}T,};;
{Rightarrow T = frac{{{R^2}}}{{5{a^2}}}sqrt {frac{{2H}}{g}} .}
]

Здесь мы снова видим аналогию с падением материального тела с высоты (H) в гравитационном поле Земли. Как известно,
время падения описывается формулой:

[T = sqrt {frac{{2H}}{g}}. ]

Если мы сравним этот результат со случаем вытекания жидкости из цилиндрического сосуда, то видно, что при тех же самых
значениях (H, R) и (a) время вытекания жидкости из конического сосуда ровно в (5) раз меньше, чем из цилиндра (хотя
объем конического сосуда меньше лишь в (3) раза!). Такие целочисленные отношения в природе выглядят удивительными, не правда ли?

Исследовать вытекание жидкости из тонкой трубки радиусом (R) и высотой (H,) считая трубку полностью заполненной жидкостью.

Аналогично разобранным выше примерам, мы можем записать уравнение баланса жидкости на некоторой произвольной высоте (z) в следующей форме:

[Sleft( z right)frac{{dz}}{{dt}} = qleft( z right).]

В данном случае площадь поперечного сечения (Sleft( z right)) является константой:

[Sleft( z right) = S = pi {R^2},]

и поток жидкости, вытекающей из сосуда, определяется формулой:

[qleft( z right) = – kz,]

где (k) зависит от размера отверстия, смачиваемости и других параметров.

В результате получаем простое дифференциальное уравнение:

[pi {R^2}frac{{dz}}{{dt}} = – kz,]

или после разделения переменных:

[frac{{dz}}{z} = – frac{k}{{pi {R^2}}}dt.]

Теперь это уравнение можно проинтегрировать, считая, что уровень жидкости уменьшается с высоты (H) до (h) за время от (0) до (t:)

[
{intlimits_H^h {frac{{dz}}{z}} = – intlimits_0^t {frac{k}{{pi {R^2}}}dt} ,};;
{Rightarrow left. {left( {ln z} right)} right|_h^H = frac{k}{{pi {R^2}}}t,};;
{Rightarrow t = frac{{pi {R^2}}}{k}left( {ln H – ln h} right) = frac{{pi {R^2}}}{k}ln frac{H}{h}.}
]

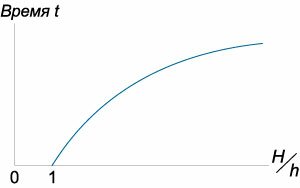
Зависимость времени (t) от отношения (largefrac{H}{h}normalsize) показана схематически на рисунке (8.)
Данная кривая аналогична зависимости времени (T) от высоты (H) для широкого цилиндрического сосуда, для которого справедлив закон Торричелли.
Интересно, что в данной простой модели время вытекания жидкости (t) формально стремится к бесконечности при (h to 0.)