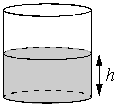
Вода в сосуде цилиндрической формы находится на уровне 40 на каком
Анонимный вопрос
21 февраля 2018 · 5,8 K
Люблю смотреть российские сериалы, играть в шахматы и путешествовать.
Возможно, имеется в виду задача:
Вода в сосуде цилиндрической формы находится на уровне h= 80 см. На каком уровне окажется вода, если её перелить в другой цилиндрический сосуд, у которого радиус основания вдвое больше, чем у первого? Ответ дайте в сантиметрах.
Решение.
Высота 1-ого цилиндра: h1= V/(πR²)=80см .
Высота 2-ого цилиндра: h2 = V/(π(2R)²)=V/(π4R²)=(1/4)*V/(πR²) =(1/4)*h1=(1/4)*80=20см.
Ответ: 20см.
а откуда взяли одну четвертую??
По какой формуле можно найти площадь цилиндра?
Любитель книг, кошек, увлекаюсь написанием рецензий
Полная площадь поверхности круглого цилиндра вычиляется так: площадь боковой поверхности цилиндра + удвоенная площадь основания.
Площадь боковой поверхности круглого цилиндра равна произведению длины окружности основания на высоту:
S=2 π rh (r – радиус, h – высота)
Основание – это круг. Площадь круга вычисляется по стандартной формуле.
Общая площадь поверхности цилиндра будет такой:
- S= 2 π rh+ 2 π r2 (обратите внимание: последняя двойка – это квадрат, т.е. r в квадрате).
Можно преобразовать так:
2 π r(h+ r).
Прочитать ещё 1 ответ
Как определить массу одной молекулы воды?
Образование: высшее (бакалавр + магистр). Увлечения: спорт, путешествие, кофе:)
Найдем массу одной молекулы воды.
1. Находим молекулярную массу воды: 16*1+1*2=18
2. Молярная масса = 18 г/моль
3. Масса 1 моля воды = 18 г
4. В 1 моле вещества содержится число Авогадро молекул 6,022*10 в 23 степени.
5. Чтобы найти массу одной молекулы, надо молярную массу разделить на число Авогадро, приблизительно будет 2,99*10 в минус 23 степени грамма.
Ответ: масса одной молекулы воды 2,99*10 в минус 23 степени грамма.
Какого вероятность того, что средняя температура на Земле станет выше 100°C?
По мере того, как Солнце постепенно расходует запасы своего водородного горючего, оно становится всё горячее, а его светимость медленно, но неуклонно увеличивается. Через 1,1 млрд лет от настоящего времени оно станет ярче на 11 %, через 3,5 млрд лет его яркость возрастёт на 40 %. К тому времени условия на Земле будут подобны условиям на Венере сегодня, а вы говорите “выше 100 градусов”… Температура будет как в аду.
Прочитать ещё 1 ответ
Как уровень воды зависит от площади дна сосуда?
Радиофизик, меньше математик, радио, сетевой админ, программист. Родом из…
Блин! Тут вопрос не о давлении! А об объёме!
Если один и тот же объём наливать в сосуды с разным по площади дном, то высота столба воды/её уровень будет зависеть от размеров дна.
Если предположить, что сосуд имеет форму параллепипеда, то уровень объёма жидкости V будет связан с дном формулой:
V = Sд * h, где Sд – площать дна, а h – уровень. Отсюда h = V/Sд, где площадь дна рассчитыаем по формуле: Sд = a * b, где а – длина сосуда, b – ширина сосуда. h в данном случае – минимальная высота сосуда, что бы влезла вся жидкость объёма V.
Для цилиндра, формула та же: V = Sд * h. Только площадь дна считается по формуле:
Sд = Пи * D в квадрате. Пи – число Пи.
Это всё случаи если сосуд или цилиндр или параллелепипед. В случае сосуда в виде шара так не посчитать, так как в данном случае в точке соприкосновения шара и поверхности площадь дан равна нулю. Тогда чтобы вычислить высоту, которую в шаре занял объём жидкости, нужно уже будет прибегать к вычислению объёма через интеграл. Тем не менее, минимальный объём шара и, следовательно, его диаметр посчитать легко – формула объёма шара известна.
V = 4/3 Пи * R в кубе, где Пи – число Пи, R – радиус шара. Если выразить R через D – диаметр шара, получим:
V = 4/3 Пи * (D/2)в кубе = 4/3 Пи * D в кубе / 8 = Пи * D в кубе / 6
Диаметр шара, полученный из этой формулы, будет минимальным, чтобы вместился весь объём:
D = Корень кубический из (6 * V / Пи).
Этот диаметр и будет высотой h для данного объёма.
Для других случаев нужно будет уже выводить всё через интеграл от объёма.
Прочитать ещё 1 ответ
Источник
ÐадаÑа â13 из 45 |
Ðода в ÑоÑÑде ÑилиндÑиÑеÑкой ÑоÑÐ¼Ñ Ð½Ð°Ñ
одиÑÑÑ Ð½Ð° ÑÑовне h= 80 Ñм. Ðа каком ÑÑовне окажеÑÑÑ Ð²Ð¾Ð´Ð°, еÑли ÐµÑ Ð¿ÐµÑелиÑÑ Ð² дÑÑгой ÑилиндÑиÑеÑкий ÑоÑÑд, Ñ ÐºÐ¾ÑоÑого ÑадиÑÑ Ð¾ÑÐ½Ð¾Ð²Ð°Ð½Ð¸Ñ Ð²Ð´Ð²Ð¾Ðµ болÑÑе, Ñем Ñ Ð¿ÐµÑвого? ÐÑÐ²ÐµÑ Ð´Ð°Ð¹Ñе
в ÑанÑимеÑÑаÑ
.
РеÑение задаÑи:
ÐÑи пеÑеливании Ð²Ð¾Ð´Ñ Ð¸Ð· одного ÑоÑÑда в дÑÑгой, обÑем водÑ, еÑÑеÑÑвенно, не менÑеÑÑÑ.
ÐÑÑÑÑ r – ÑадиÑÑ Ð¾ÑÐ½Ð¾Ð²Ð°Ð½Ð¸Ñ Ð¿ÐµÑвого ÑоÑÑда.
Тогда плоÑÐ°Ð´Ñ Ð¾ÑнованиÑ:
S=πr2
ÐбÑем водÑ:
V=S*h=πr2h
ÐлоÑÐ°Ð´Ñ Ð¾ÑÐ½Ð¾Ð²Ð°Ð½Ð¸Ñ Ð²ÑоÑого ÑоÑÑда:
S2=πR2=π(2r)2=4πr2 (R – ÑадиÑÑ Ð²ÑоÑого ÑоÑÑда = 2r, по ÑÑловиÑ)
ÐбÑем водÑ:
V2=S2*h2=4πr2h2
Ðак Ð¼Ñ Ñже Ñказали Ñанее обÑем Ð²Ð¾Ð´Ñ Ð½Ðµ менÑеÑÑÑ, Ñ.е. V=V2, полÑÑаем:
πr2h=4πr2h2 |:πr2
h=4h2
80=4h2
h2=80/4=20
ÐÑвеÑ: 20
ÐоделиÑеÑÑ ÑеÑением
ÐÑиÑоединÑйÑеÑÑ Ðº нам…
ÐÑ Ð¼Ð¾Ð¶ÐµÑе поблагодаÑиÑÑ Ð°Ð²ÑоÑа, напиÑаÑÑ Ñвои пÑеÑензии или пÑÐµÐ´Ð»Ð¾Ð¶ÐµÐ½Ð¸Ñ Ð½Ð°
ÑÑÑаниÑе ‘ÐÑо нађ
ÐÑÑгие задаÑи из ÑÑого Ñаздела

ÐадаÑа â4E4948
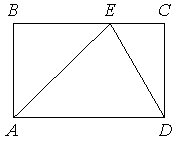Ðа ÑÑоÑоне BC пÑÑмоÑголÑника ABCD, Ñ ÐºÐ¾ÑоÑого AB=12 и AD=17, оÑмеÑена ÑоÑка E Ñак, ÑÑо ÑÑеÑголÑник ABE ÑавнобедÑеннÑй. ÐайдиÑе ED.

ÐадаÑа âF87A44
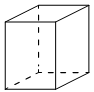Ðва ÑебÑа пÑÑмоÑголÑного паÑаллелепипеда ÑÐ°Ð²Ð½Ñ 8 и 5,
а обÑÑм паÑаллелепипеда Ñавен 280. ÐайдиÑе плоÑÐ°Ð´Ñ Ð¿Ð¾Ð²ÐµÑÑ
ноÑÑи ÑÑого паÑаллелепипеда.

ÐадаÑа â255A4D
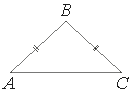Ð ÑавнобедÑенном ÑÑеÑголÑнике ABC Ð±Ð¾ÐºÐ¾Ð²Ð°Ñ ÑÑоÑона AB=25, sinA=3/5. ÐайдиÑе плоÑÐ°Ð´Ñ ÑÑеÑголÑника ABC.

ÐадаÑа â8BF84A
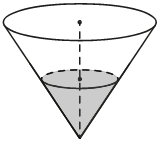Ð ÑоÑÑде, имеÑÑем ÑоÑÐ¼Ñ ÐºÐ¾Ð½ÑÑа, ÑÑÐ¾Ð²ÐµÐ½Ñ Ð¶Ð¸Ð´ÐºÐ¾ÑÑи доÑÑÐ¸Ð³Ð°ÐµÑ 1/2 вÑÑоÑÑ. ÐбÑÑм ÑоÑÑда 1600 мл. Ð§ÐµÐ¼Ñ Ñавен обÑÑм налиÑой жидкоÑÑи? ÐÑÐ²ÐµÑ Ð´Ð°Ð¹Ñе в миллилиÑÑаÑ
.

ÐадаÑа â87AE44
Ðа кооÑдинаÑной пÑÑмой оÑмеÑÐµÐ½Ñ ÑоÑки A, B, C и D.
ЧиÑло m Ñавно √2.
УÑÑановиÑе ÑооÑвеÑÑÑвие Ð¼ÐµÐ¶Ð´Ñ ÑказаннÑми ÑоÑками и ÑиÑлами в пÑавом ÑÑолбÑе, коÑоÑÑе им ÑооÑвеÑÑÑвÑÑÑ.
| ТÐЧÐÐ | ЧÐСÐÐ |
| A | 1) 2m-5 |
| B | 2) m3 |
| C | 3) m-1 |
| D | 4) -1/m |
ÐпиÑиÑе в пÑиведÑннÑÑ Ð² оÑвеÑе ÑаблиÑÑ Ð¿Ð¾Ð´ каждой бÑквой ÑооÑвеÑÑÑвÑÑÑий ÑиÑÐ»Ñ Ð½Ð¾Ð¼ÐµÑ.
Источник