Вода во вращающемся сосуде

Возьмем открытый цилиндрический сосуд с жидкостью и сообщим ему постоянную угловую скорость w вращения вокруг вертикальной оси. Жидкость постепенно приобретет ту же угловую скорость, что и сосуд, а свободная поверхность ее видоизменится: в центральной части уровень жидкости понизится, у стенок – повысится, и вся свободная поверхность жидкости станет некоторой поверхностью вращения (рис. 2.11).

На жидкость в этом случае будут действовать две массовые силы, сила тяжести и центробежная сила, которые, будучи отнесенными к единице массы, соответственно равны g и w2r. Равнодействующая массовая сила j увеличивается с увеличением радиуса за счет второй составляющей, а угол наклона ее к горизонту уменьшается. Эта сила нормальна к свободной поверхности жидкости, поэтому угол наклона поверхности к горизонту возрастает с увеличением радиуса. Найдем уравнение положения свободной поверхности.

Рис. 2.11

Учитывая, что сила j нормальна к свободной поверхности, получим

отсюда
или после интегрирования
В точке пересечения свободной поверхности с осью вращения C = h, поэтому окончательно будем иметь
                                       (2.10)
т. е. свободная поверхность жидкости является параболоидом вращения.

Максимальную высоту подъема жидкости можно определить исходя из равенства объемов неподвижной жидкости и жидкости во время вращения.
На практике очень часто приходится иметь дело с вращением сосуда, заполненного жидкостью, вокруг горизонтальной оси. При этом угловая скорость w столь велика, что сила тяжести на порядок меньше центробежных сил, и ее действие можно не учитывать. Закон изменения давления в жидкости для этого случая получим из рассмотрения уравнения равновесия элементарного объема с площадью основания dS и высотой dr, взятой вдоль радиуса (рис. 2.12). На выделенный элемент жидкости действуют силы давления и центробежная сила.

Обозначив давление в центре площадки dS, расположенной на радиусе r, через p, а в центре другого основания объема (на радиусе r + dr) через p + dp, получим следующее уравнение равновесия выделенного объема в направлении радиуса

или

Рис. 2.12

После интегрирования

Постоянную C найдем из условия, что при r = r0 p = p0.
Следовательно

Подставив ее значение в предыдущее уравнение, получим связь между p и r в следующем виде:
(2.11)
Очевидно, что поверхностями уровня в данном случае будут цилиндрические поверхности с общей осью – осью вращения жидкости.

Часто бывает необходимо определить силу давления вращающейся вместе с сосудом жидкости на его стенку, нормальную к его оси вращения. Для этого определим силу давления, приходящуюся на элементарную кольцевую площадку радиусом r и шириной dr. Используя формулу (2.11), получим

а затем следует выполнить интегрирование в требуемых пределах.

При большой скорости вращения жидкости получается значительная суммарная сила давления на стенку. Это используется в некоторых фрикционных муфтах, где для сцепления двух валов требуется создание больших сил давления.

Источник

Рассмотрим случай, когда на жидкость, помимо объемных сил тяжести, действует еще другая система объемных сил, например, система центробежных сил инерции.

Возьмем круглоцилиндрический сосуд, наполненный жидкостью, причем будем считать, что этот сосуд вращается вокруг своей вертикальной оси равномерно, т. е. с постоянной угловой скоростью (рис. 2-14). Благодаря силам трения стенки вращающегося сосуда будут вначале увлекать за собой жидкость, а по истечении некоторого времени вся жидкость начнет вращаться вместе с сосудом с той же угловой скоростью Ω, находясь по отношению к стенкам сосуда в покое. Силы трения при этом внутри жидкости, а также между жидкостью, стенками сосуда и его дном, будут отсутствовать.

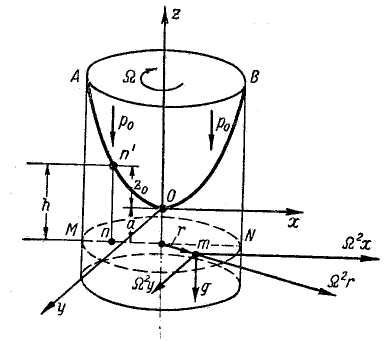
Вода во вращающемся сосуде

Рис. 2-14. Цилиндрический сосуд, вращающийся относительно вертикальной оси Oz

АОВ — свободная поверхность жидкости

Если оси координат, расположенные, как показано на чертеже, будем считать скрепленными с вращающимся сосудом, то по отношению к таким вращающимся осям координат жидкость также будет находиться в покое. Поэтому для исследования вращающейся жидкости при указанных подвижных осях координат могут быть применены известные уравнения Эйлера (2-14).

В эти уравнения входит объемная сила 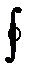Вода во вращающемся сосуде , действующая на единицу массы жидкости. В данном случае сила 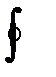будет слагаться из двух сил: силы тяжести и центробежной силы.

С тем чтобы найти проекцию центробежной силы на оси координат, наметим внутри жидкости точку т и выделим у нее элементарную массу жидкости δM. Масса δM будет вращаться вокруг оси сосуда, двигаясь по окружности, имеющей радиус r и лежащей в плоскости, нормальной к оси сосуда. Центробежная сила, действующая на данную массу, будет

I’= 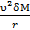Вода во вращающемся сосуде , (2-62)

где υ – скорость движения массы δM по окружности радиуса r.

Центробежная сила, отнесенная к единице массы жидкости, сосредоточенной в точке т,

I = 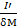Вода во вращающемся сосуде = Ω2r. (2-63)

Эта сила, так же как и сила I’, направлена по радиусу от оси сосуда наружу. Проекции силы I (отнесенной к единице м- ассы) на оси координат

Ix = Ω2rcos(r,x) = Ω2x

Iy = Ω2rcos(r,y) = Ω2y

Iz = 0 (2-64)

Проекции объемной силы тяжести, отнесенной к единице массы, выражаются зависимостью (2-28). Складывая объемные силы тяжести и объемные центробежные силы, отнесенные к единице массы, получаем

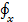Вода во вращающемся сосуде = 0 +Ω2x = Ω2x;

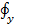Вода во вращающемся сосуде = 0 + Ω2y = Ω2y;

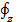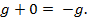Вода во вращающемся сосуде = – (2-65)

Подставляя (2-65) в (2-17), найдем

dpA = ρ(Ω2xdx + Ω2ydy – 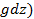Вода во вращающемся сосуде , (2-66)

что после интегрирования дает

dpA = ρ( 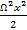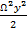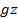Вода во вращающемся сосуде + – ) + C = 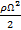(x2 + y2) – ρ 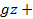C. (2-67)

Постоянную интегрирования С устанавливаем, написав (2-67) применительно к точке, находящейся в начале координат, для которой x = y = z =0; p = p0. Как видно,

C = p0 (2-68)

причем (2-67) перепишется в виде:

pA = p0 + 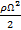Вода во вращающемся сосуде (x2 +y2) – γz (2-69)

Это последнее уравнение и выражает закон распределения давления в рассматриваемой жидкости. Пользуясь таким уравнением, можно найти поверхности равного давления.

Действительно, уравнение поверхности, во всех точках которой давление pA = pi= const, запишется в виде

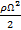Вода во вращающемся сосуде (x2 +y2) – γz = pi – p0. (2-70)

Уравнение (2-70) выражает поверхность, являющуюся параболоидом вращения (с вертикальной осью).

Свободная поверхность жидкости, характеризуемая постоянным давлением pi = p0, представляет собой также параболоид вращения; уравнение ее будет:

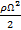Вода во вращающемся сосуде (x2 +y2) – γz = 0. (2-71)

Если учесть, что x2 + y2 = r2, то, решив (2-71) относительно z, получим следующее уравнение, по которому легко построить параболу АОВ, дающую свободную поверхность:

z0 = 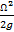Вода во вращающемся сосуде r2 (2-72)

где z0- ордината кривой АОВ.

Распределение давления в горизонтальной плоскости MN, лежащей ниже начала координат на величину a, можно найти, пользуясь (2-69):

pA = p0 + 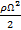Вода во вращающемся сосуде (x2 +y2) +γa = p0 + ρ 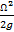r2+ γa = p0 + γ( 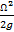r2+ a). (2-73)

Учитывая (2-72), получаем

pA = p0 + γ(a + z0) = p0 + γh (2-74)

где h = a +z0 показано на рис. 2-14.

Таким образом, давление в жидкости, находящейся внутри равномерно вращающегося сосуда, выражается зависимостью того же вида, что и для случая тяжелой покоящейся жидкости [см. (2-39)]; под величиной h здесь надо понимать только заглубление рассматриваемой точки под криволинейной свободной поверхностью.

Источник

Сегодня я заварил себе чай и задумался

Сегодня утром я задумался, пока размешивал два кубика сахара в чашке с только что заваренным чаем. Задумался о форме жидкости, которую она принимает при вращении. Безусловно, все представляют себе что будет, если очень быстро начать размешивать сахар в чашке с чаем. Мне захотелось рассмотреть этот банальный и привычный процесс подробнее и попытаться рассказать Вам немного интересного из физики окружающих нас в быту явлений.

Идея эксперимента

Давайте представим, что мы имеем некоторую цилиндрическую тару, в которой находится некоторая жидкость. Вращаться жидкость можно заставить, как минимум, двумя очевидными способами: размешать её каким-нибудь предметом или начать вращать цилиндрическую тару, что, благодаря силам трения между жидкостью и поверхностью сосуда, приведет к вращению жидкости, увлекаемой содержащим её вращающимся сосудам.

Физическая модель

Остановимся на втором варианте. Итак, у нас есть вращающийся с постоянной циклической частотой сосуд, в котором при динамическом равновесии с постоянной циклической частотой вращается жидкость в том же направлении.

Вырежем из всей жидкости элементарный бесконечно малый объем около поверхности и рассмотрим какие силы на него действуют. В силу симметрии задачи, будем ориентироваться на цилиндрические координаты, что заметно упростит расчеты.

Качественный расчет формы поверхности

Запишем второй закон Ньютона для элементарного кусочка объема жидкости:

К примеру, после размешивания ложкой сахара в чашке только что заваренного чая, жидкость вращается вокруг оси симметрии, отсюда наш элементарный кусочек объема имеет центростремительное ускорение. Поэтому спроецируем наш закон Ньютона на ось, совпадающую с радиусом-вектором от элементарного объема до оси симметрии. Не будем учитывать вязкость и поверхностное натяжение. Сила, сообщающая центростремительное ускорение (в правой части нашего закона движения) возникнет из-за разности давлений столбов жидкости, что можно увидеть на увеличенной части первого рисунка.

Таким образом, у нас получится следующее выражение:
, где , а та самая сила определится как , где площадью эффективного сечения обозначена та площадь нашего элементарного объема, на которую действует разница давлений столбов жидкости .
Получаем силу

Масса нашего элемента объема определяется по знакомой всем формуле , а сам объем будет равен (элементарный объем в цилиндрических координатах).
В итоге, 2 закон Ньютона для нашей маленькой задачки расписывается в следующее выражение:

После небольших сокращений и преобразований получаем:

Теперь проинтегрируем обе части выражения, используя неопределенные интегралы:

Детальный расчет формы поверхности

Теперь мы получили вполне ясную зависимость для формы поверхности и с уверенностью можем сказать, что это параболоид. Но нам неизвестна постоянная величина . Давайте её определим для полного понимания физики процесса.

Так как объем жидкости не меняется (мы считаем, что не пролили ни капли, пока размешивали наш чай ツ), то запишем объемы до вращения и во время вращения с постоянной циклической частотой.

До вращения:
, где — это высота жидкости в цилиндрической поверхности в спокойном состоянии (вращения нет).

Во время вращения:

Данные объемы равны, поэтому:

Отсюда выражается ранее неизвестная постоянная:
И окончательное уравнение формы поверхности вращающейся жидкости имеет вид:
или преобразовав

Некоторые заметки

Хотелось бы обратить внимание на то, что форма поверхности зависит от частоты вращения, ускорения свободного падения, геометрических параметров сосуда, первоначального объема жидкости, но не зависит от плотности жидкости. Это выражение мне показалось довольно интересным, так как с его помощью можно легко смоделировать примерное расположение жидкости внутри вращающегося вокруг своей оси симметрии цилиндрического сосуда. Для этого можно воспользоваться MathCAD’ом и построить несколько графиков.

Графическое представление результатов расчета

Возьмем вполне реальные параметры системы, соизмеримые с размерами чашки или стакана.
Радиус цилиндрической поверхности:
Высота жидкости в цилиндрической поверхности без вращения:
Ускорение свободного падения:
Циклическая частота вращения цилиндрической поверхности:
(Все значения этих величин заданы в системе Си)

Далее перепишем нашу функцию для её отображения в MathCAD.
Для 2D отображения сечения:

Для 3D отображения поверхности:

В качестве изменяющегося параметра будем менять циклическую частоту вращения . Результаты можно наблюдать на рисунках ниже:

При циклической частоте

Выводы

Видно, что если циклическая частота превысит значение , то мы увидим дно вращающегося цилиндрического сосуда, и, начиная с этой частоты, жидкость будет плавно «переходить» на стенки сосуда, всё сильнее оголяя дно. Очевидно, что при очень больших частотах вся жидкость растечется по стенкам сосуда. Теперь мы знаем все параметры такой жидкости. Зная её уравнение, не составит большого труда рассчитать толщину слоя жидкости на стенке сосуда на определенной высоте при определенной частоте.

upd. Отдельно хотелось бы подчеркнуть те противоречащие друг другу допущения, которые были приняты при рассмотрении задачи:
1. Считалось что, жидкость вращается благодаря вращению сосуда, который её содержит. Это может быть только при учете внутреннего трения, вязкости и поверхностного натяжения.
2. Но при выводе формы поверхности эти явления не учитываются для того, чтобы упростить решение и показать только качественный результаты моделирования. Т.е. решение немного противоречит описываемой изначально модели. Учет всех явлений, включая нелинейность процесса при высоких частотах, настолько бы усложнил задачу, что её вряд ли можно было бы решить аналитически и показать примерную и понятную модель для человека, который не связан с математикой/физикой.
3. Цель состоялась в том, чтобы показать лишь очень приближенное и самое простое решение, включающее в себя ряд допущений.

Источник

Вращение сосуда с жидкостью вокруг вертикальной оси

Рис. 2.15

На жидкость в этом случае будут действовать две массовые силы, сила тяжести и центробежная сила, которые, будучи отнесенными к единице массы, соответственно равны g и . Равнодействующая массовая сила j увеличивается с увеличением радиуса за счет второй составляющей, а угол наклона ее к горизонту уменьшается. Эта сила нормальна к свободной поверхности жидкости, поэтому угол наклона поверхности к горизонту возрастает с увеличением радиуса. Найдем уравнение положения свободной поверхности.

Учитывая, что сила нормальна к свободной поверхности, получим , отсюда или после интегрирования .

В точке пересечения свободной поверхности с осью вращения C=h и r=0, поэтому окончательно будем иметь

, (2.10)

где .

Таким образом, свободная поверхность жидкости является параболоидом вращения. Максимальную высоту подъема жидкости можно определить, используя выражение (2.10) и исходя из равенства объемов неподвижной жидкости и жидкости во время вращения.

Читайте также: Лопается сосуд при кашле

Запишем закон изменения давления во вращающейся жидкости в функции радиуса и глубины относительно верхней точки жидкости (без вывода):

Вращение сосуда с жидкостью вокруг горизонтальной оси

При таком вращении угловая скорость w столь велика, что (действие силы тяжести можно не учитывать). Закон изменения давления в жидкости для этого случая получим из рассмотрения уравнения равновесия элементарного объема с площадью основания dS и высотой dr, взятой вдоль радиуса (рис. 2.16). На выделенный элемент жидкости действуют силы давления и центробежная сила.

Рис. 2.16

Обозначив давление в центре площадки dS, расположенной на радиусе r, через p, а в центре другого основания объема (на радиусе r + dr) через p + dp (разложили p в ряд Тейлора, но так как в данном случае p зависит только от r, то dr/dr сократился), получим следующее уравнение равновесия выделенного объема в направлении радиуса

или .

После интегрирования получим . Постоянную C найдем из условия, что при r = rp = p0, следовательно, .

Подставив ее значение в предыдущее уравнение, получим связь между p и r в следующем виде:

. (2.11)

Очевидно, что поверхностями уровня в данном случае будут цилиндрические поверхности с общей осью – осью вращения жидкости.

а затем следует выполнить интегрирование в требуемых пределах:

Если равно внешнему давлению, то .

При большой скорости вращения жидкости получается значительная суммарная сила давления Fб на боковую стенку. Это используется в некоторых фрикционных муфтах, где для сцепления двух валов требуется создание больших сил давления.

Приведем выражение для определения силы Fб без вывода:

, где – длина цилиндра.

Источник

Работа 3. Исследование формы поверхности жидкости во вращающемся сосуде
(10-й класс)

Цель работы

Получить аналитическое выражение для кривой, образуемой поверхностью воды в плоской кювете, вращающейся с постоянной угловой скоростью, связать коэффициенты функции с характеристиками жидкости и параметрами вращения.

Теоретические основы работы

Рассмотрим жидкость, вращающуюся вместе с сосудом с угловой скоростью w вокруг вертикальной оси OY. Оси координат инерциальной системы отсчета выберем так, как показано на рисунке.

Вода во вращающемся сосуде

Рассмотрим условие равновесия вертикального столбика жидкости АВ = y, находящегося на расстоянии x от оси вращения. Если площадь DS основания столбика мала, условие равновесия столбика вдоль оси OY запишется как

где m =ryDS – масса столбика, p0 – атмосферное давление, p1 – давление у основания столбика. Тогда

(1)

Согласно закону Паскаля, давление p1 характеризует силу воздействия жидкости в окрестности точки А как на вертикальный столб АВ снизу, так и на горизонтальный столб АО слева. Поэтому для определения p1 рассмотрим движение горизонтального столбика ОА того же поперечного сечения DS, вращающегося вокруг оси OY. Он вращается как твердое тело. Для описания вращающегося твердого тела воспользуемся теоремой о движении центра масс столбика, находящегося в точке с координатами :

Здесь – масса горизонтального столбика, – сумма всех сил, действующих на горизонтальный столбик OA. В проекции на ось OX это уравнение запишется как

Проекция ускорения центра масс столбика при его движении по окружности

тогда

(2).

Сопоставляя это выражение с уравнением (1), получим , то есть кривая y(x) в сечении жидкости плоскостью OXY описывается функцией , графиком которой является парабола с вершиной в точке О.

Следовательно, поверхность жидкости является поверхностью, образованной вращением параболы вокруг оси OY.

Оборудование

· ПК с программой для видеоанализа

· Плоская пластиковая кювета с подкрашенной водой

· Электродвигатель

· Нить

· Штатив с лапкой для крепления электродвигателя

· Видеокамера (фотоаппарат с функцией видеосъемки) на штативе

Порядок проведения эксперимента

Соберите установку согласно схеме.

Вода во вращающемся сосуде

Сфотографируйтесь рядом с установкой. Замкните ключ, дождитесь, когда кювета раскрутится до вращения с постоянной скоростью, и снимите вращение кюветы с водой фотоаппаратом, работающим в режиме видеосъемки, или на видеокамеру в течение нескольких секунд. Объектив камеры должен располагаться на расстоянии не менее 1 м от кюветы напротив середины ее большей вертикальной грани. Ось объектива – горизонтальна.

4. Отключите электродвигатель от блока питания и замерьте высоту (ширину) кюветы.

5. Загрузите файлы с результатами фото – и видеосъемки на ваш рабочий компьютер, используя специальный кабель.

Обработка и анализ результатов

(описание для обработки в программе «1С:Измеритель»).

1. Загрузите в программу «1С:Измеритель» для обработке фото и видео видеофайл с вращающейся кюветой. Если видеофайлы имеют расширение, иное от *.avi и *.wmv (например, *.mov), то следует воспользоваться стандартными конверторами видеофайлов и перевести их в этот формат.

Проводя покадровый просмотр видеофайла, найдите кадр, где большая грань кюветы находится в плоскости, перпендикулярной оси объектива камеры. Используя кнопку «t=0», выберите этот кадр за начало отсчета. Листая по кадрам видеофайл, найдите следующий кадр, когда кювета с водой, совершив один оборот, оказалась в таком же положении, и, используя инструмент «Точка» , пометьте этот кадр. В таблице результатов во вкладке «Точки» должны появится номер и время кадра, на котором вы поставили «Точку». Пролистайте таким образом кадры, в течение которых груз совершит 10 оборотов вокруг оси вращения. Для того чтобы не ошибиться в счете, рекомендуется после каждого полного оборота кюветы ставить на кадре «Точку». Тогда в таблице будет заполнено 10 строк с номером кадра и временем его фиксирования после начала отсчета. Экспортируйте данные по периоду вращения груза в программу обработки результатов Excel, воспользовавшись в таблице с результатами измерения кнопкой «Экспорт таблиц в Excel». Если вы не фиксировали каждый полный оборот кюветы установкой «Точки» на экране и число строк таблицы не соответствует числу оборотов кюветы, то рекомендуется на этом этапе ввести в таблице Excel дополнительный столбец «N», показывающий число оборотов кюветы за время, зафиксированное в строке.

Точки
Подпись	Кадр	Время, с.	X, м.	Y, м.	N
Точка 1	5
Точка 2	124	4,76	10
Точка 3	244	9,56	20
Точка 4	304	11,96	25

Сохраните файл с таблицей в виде отдельного файла с названием «Таблица 1.xls». В загруженном видеофайле найдите кадр, в котором большая вертикальная плоскость кюветы перпендикулярна оси объектива камеры, с помощью которой проводилась видеосъемка. Зафиксируйте положение точек поверхности вращающейся жидкости в выбранной системе координат:

– установите систему координат Вода во вращающемся сосуде на кадр. Рекомендуется ось OX расположить вертикально, начало координат поместить в самой нижней точке поверхности вращающейся жидкости;

– растяните масштабный отрезок вдоль вертикального ребра кюветы и введите его реальную длину и единицы измерения в соответствующие окна на экране «Измерителя по обработке фото и видео»;

– используя инструмент «Точка» Вода во вращающемся сосуде , поставьте 15–20 точек вдоль всей линии показывающей форму поверхности жидкости во вращающейся кювете. В таблице элементов на вкладке «Точки» появятся номер кадра, на котором вы проводите фиксирование формы поверхности, и координаты всех поставленных точек в выбранной системе координат;

Вода во вращающемся сосуде

– экспортируйте таблицу в Excel с помощью соответствующей кнопки и сохраните файл с этими данными в редакторе таблиц Excel, присвоив ему название «Таблица2.xls».

Сохраните вид экрана с результатами обработки в виде рисунка, перенесите вид экрана в Буфер обмена (кнопка Print Screen на клавиатуре), а затем в любой графический редактор, например Paint, и сохраните рисунок в виде файла с названием, например «Результат обработки 1.jpg». Этот файл понадобится вам для подготовки отчета. Сохраните на всякий случай результаты обработки данного кадра, воспользовавшись в программе «Измеритель по обработке фото и видео» опцией Файл – Сохранить проект и дав проекту название, например «Проект 1.rul». Это позволит при обнаружении в дальнейшей работе с полученными данными неверных действий на данном этапе вернуться к повторной обработке того же файла с того же места.

Вода во вращающемся сосуде

Обработку результатов можно произвести в редакторе таблиц Excel, используя его возможности для графического представления информации из таблиц. Рекомендуется воспользоваться Шаблоном для обработки данных работы «Исследование формы поверхности жидкости во вращающемся сосуде», в который можно загрузить данные из файлов «Таблица1.xls» и «Таблица2.xls» путем копирования содержимого ячеек или соответствующих фрагментов таблиц. В шаблоне имеется два листа – «Период вращения кюветы» и «Данные по одной точке».

Вода во вращающемся сосуде

Ячейки таблицы, окрашенные желтым, должны быть заполнены данными из таблицы в файле «Таблица1.xls», столбец «Число оборотов N от начала отсчета» вручную, если не был заготовлен заранее в файле «Таблица1.xls».

Ошибка измерения времени на экране Dt = 0,04 с внесена в Шаблон заранее, как время смены одного кадра на экране. Если вы используете более совершенную камеру
(с большим числом кадров в 1 с), точность будет другая и вам следует изменить данные в столбце «Ошибка измерения времени Dt, с».

Заполнение ячеек в первых четырех столбцах приводит к автоматическому заполнению остальных ячеек, окрашенных зеленым. Так, относительная ошибка в определении периода считается относительной ошибкой измерения времени (Dt/t)×100%, а ее окончательное значение выбирается минимальным из всех полученных, значение периода и абсолютная ошибка периода считаются исходя из строчки с минимальной относительной ошибкой периода. В данном примере – на основании последней строки T=11,96/25=0,478 c, DT=T×(0.3%/100%)=0,001 c.

Вид Шаблона на листе «Данные по одной точке» показан ниже.

Вода во вращающемся сосуде

В желтые ячейки таблицы копируются значения из «Таблица2.xls». В правой части имеется инструментарий для графика экспериментальных данных Y(X) и сопоставления этого графика c графиками функций, приведенных в списке типовых функций на странице. Данные в ячейки, окрашенные фиолетовым цветом, вводятся с клавиатуры при уточнении коэффициентов подбираемых функций. На рисунке синим показан график экспериментальных данных, а красным – график функции Y=Аln|X|+B при значениях А=1 и В=1.

Внимание! Аналитический вид функциональной зависимости, описываемый данным графиком, сильно зависит от расположения системы координат. Если вы решите, что вы неудачно выбрали начало или направление осей OX и OY, то можно вернуться к обработке кадра видео с выбором системы координат и нанесением точек вдоль линии, отображающей форму поверхности жидкости в кювете (п. 6 раздела Порядок проведения измерений с использованием «Измерителя по обработке фото и видео»).

Для этого можно, открыв «Измеритель по обработке фото и видео», загрузить старый проект (файл «Проект 1.rul», который вы создали перед закрытием программы «Измеритель по обработке фото и видео»). После загрузки проекта можно выбрать опцию Правка – Выделить все, стереть результаты предыдущей работы и выбрать новое расположение системы отсчета, масштабного отрезка и нанести новые точки на кадр.

Вопросы и задания для предварительного опроса и защиты ЛР

Распечатайте кадр с вращающейся жидкостью, на котором кювета повернута большей боковой гранью перпендикулярно к оси видеосъемки. Выделите на нем фрагмент жидкости вблизи границы раздела вода – воздух и изобразите силы, действующие на этот фрагмент. Куда направлена равнодействующая сил, действующих на выделенный фрагмент жидкости? Одинаково ли давление во всех точках вращающейся жидкости, находящихся на горизонтальной прямой, проходящей через нижнюю точку границы раздела воздух–жидкость? Как связаны координаты X и Y точек, лежащих на границе раздела жидкость – воздух в кювете, вращающейся с периодом Т в системе координат, оси которой расположены вертикально и горизонтально, а начало координат расположено в нижней точке С границы раздела? Как будет выглядеть зависимость Y(X) в системе координат, сдвинутой относительно точки С (см. п. 4) на расстояние d вправо? влево? вверх? вниз? с осью OY, повернутой вниз? Вода налита в сосуд в форме параллелепипеда высотой и шириной 10 см и в состоянии покоя заполняет его на одну треть. При какой частоте вращения покажется дно сосуда? жидкость начнет выливаться через край сосуда?

Отчет

Отчет рекомендуется готовить в текстовом редакторе Word, доступном на школьных компьютерах и знакомом вам по урокам информатики. Вы сможете вставить в него различные данные и графические иллюстрации, подготовленные в ходе выполнения работы, путем копирования фрагментов цифровых ресурсов.

Отчет обязательно должен содержать:

1) фамилии и имена, класс, исполнителей работы с фотографией на фоне установки;

2) вид установки с выносками, поясняющими названия и предназначение ее компонентов (электродвигатель, крепеж, кювета, источник питания), описание условий фото – и видеосъемки (тип фотоаппарата, число кадров в секунду, разрешение матрицы, расстояние до установки и расположение точки съемки относительно кюветы);

3) таблицу исходных данных по измерению периода вращения кюветы и итоговые числовые значения периода с указанием точности измерений;

4) рисунок, иллюстрирующий процедуру фиксирования формы поверхности жидкости на экране компьютера с демонстрацией положения системы координат и масштабного отрезка;

5) таблицу исходных данных по координатам точек на границе вода–воздух на кадре с вращающейся кюветой.

6) график, показывающий степень соответствия экспериментальных данных и теоретической аналитической зависимости при указанных коэффициентах;

7) вывод по следующему образцу.

Вывод

При w0 = 0 форма поверхности описывается прямой y=.

При w1 =____ с-1 наблюдаемая форма поверхности описывается кривой с уравнением f(X)=__________

где А=____, В=______, С=______

Это с теоретической зависимостью ___________________, из которой можно, зная значение w1 =______, с-1 и А=_____ , оценить значение ускорения свободного падения g»______ .

Источник