Воздух в открытом сосуде медленно нагрели от 20 до 200
За это задание ты можешь получить 1 балл. Уровень сложности: базовый.
Средний процент выполнения: 64%
Ответом к заданию 10 по физике может быть целое число или конечная десятичная дробь.
Задачи для практики
Задача 1
Сколько керосина необходимо сжечь, чтобы 50 л воды нагреть от 20◦C до кипения? КПД нагревателя равен 35%. Удельная теплота сгорания керосина 4,3 · 107 Дж/кг. Ответ выразите в (кг), округлив до десятых.
Решение
Дано:
$V=50·10^{-3}м^3$
$ρ_в=10^3{кг}/{м^3}$
$t_1=20°C; t_2=100°C; η=0.35$
$q=4.3·10^7$Дж/кг
$c=4200$Дж/кг·К
$m-?$
Решение:
$Q_1=q·m$(1) – количество теплоты, которое выделяется при сжимании керосина, $m$ – масса керосина. $Q_2=c·m_в·(t_2-t_1)=c·ρ·V·(t_2-t_1)$(2) – количество теплоты, которое необходимо затратить, чтобы нагреть воду массой $m_в=ρ·V$(3), где $ρ$ – плотность воды, $c$ – удельная теплоемкость воды.
КПД нагревателя определяется выражением: $η={A_{полез}}/{A_{затр}}·100%={c·ρ·V·(t_2-t_1)}/{q_m}·100%$(4), откуда $m={c·ρ·V·(t_2-t_1)·100%}/{q·η}$(5). Подставим в (5): $m={4200·10^3·50·10^{-3}·(100-20)·100%}/{4.3·10^7·35%}={4.2·5·8}/{4.3·35}=1.1$кг.
Ответ: 1.1
Показать решение
Полный курс
Задача 2
В подвальном помещении относительная влажность воздуха 70%, а парциальное давление водяных паров 2100 Па. Чему равно давление насыщенных паров при той же температуре? Ответ выразите в (кПа).
Решение
Дано:
$p=2100$Па
$ϕ=70%$
$p_н-?$
Решение:
Относительная влажность воздуха равна: $ϕ={p}/{p_н}·100%$, откуда давление насыщенных паров $p_н$ равно: $p_н={p·100%}/{ϕ}={2100·100%}/{70%}=3000=3$кПа.
Ответ: 3
Показать решение
Полный курс
Задача 3
Определите КПД нагревателя, расходующего 80 г керосина на нагревание 3 л воды на 90 К. Удельная теплота сгорания керосина 4,3·107 Дж/кг. Ответ выразите в (%).
Решение
Дано:
$m_к=0.08$кг
$V_в=3=3·10^{-3}м^3$
$ρ_в=1000{кг}/{м^3}$
$∆T=90K$
$q=4.3·10^7$Дж/кг
$c=4200$Дж/кг·К
$η-?$
Решение:
КПД нагревателя определяется выражением: $η={A_{полез}}/{A_{затр}}·100%$(1), $m_в=ρ_в·V_в$(2) – масса воды, где $A_{полез}=Q_п=cm_в·∆T=c·ρ_в·V_в·∆T$(3) – полезная работа; $A_{затр}=Q_з=q·m_к$(4) – затраченная (полезная) работа. Подставим (3) и (4) в (1) получим: $η={c·ρ_в·V_в·∆T}/{q·m_к}·100%={4200·10^3·3·10^{-3}·90}/{4.3·10^7·8·10^{-2}}·100%={1134000}/{3440000}·100%=32.965%=33%$.
Ответ: 33
Показать решение
Полный курс
Задача 4
Определите относительную влажность воздуха при комнатной температуре, если парциальное давление пара при этой температуре равно 1167 Па, а давление насыщенного пара равно 2333 Па. Ответ выразите в (%).
Решение
Дано:
$p=1167$Па
$p_0=2333$Па
$ϕ-?$
Решение:
Относительная влажность воздуха равна: $ϕ={p}/{p_0}·100%$, где $p$ – парциальное давление пара, $p_0$ – давление насыщенного пара. Подставим числа: $ϕ={1167}/{2333}·100%=0.5·100%=50%$.
Ответ: 50
Показать решение
Полный курс
Задача 5
Относительная влажность воздуха 65%, давление насыщенного пара в нём при некоторой температуре равно 3,4 кПа. Чему равно парциальное давление пара при этой же температуре? Ответ выразите в (кПа).
Решение
Дано:
$ϕ=65%$
$p_0=3.4·10^3$Па
$p-?$
Решение:
По определению относительная влажность воздуха равна: $ϕ={p}/{p_0}·100%$(1), где $p$ – парциальное давление пара. Из (1) найдем $p$: $p={ϕ·p_0}/{100%}$(2). Подставим числа: $p={65·3.4·10^3}/{100%}=2210=2.21$кПа.
Ответ: 2.21
Показать решение
Полный курс
Задача 6
Относительная влажность воздуха в закрытом сосуде под поршнем составляет 65%. Какой станет относительная влажность воздуха в сосуде, если объём воздуха в нём изотермически уменьшить в 2 раза за счёт движения поршня? Ответ выразить в (%).
Решение
Дано:
$T=const$
$ϕ_{от.в.}=65%$
$V_2={V_1}/{2}$
Решение:
Из теории известно, что при $T=const$ и уменьшении объема, увеличивается давление по закону Менделеева-Клайперона $PV=υRT$. Тогда как $P∼ϕ_{от.в.}$, но более чем 100% быть не может.
Ответ: 100
Показать решение
Полный курс
Задача 7
Относительная влажность воздуха при температуре 100◦С составляет 60%. Чему равно парциальное давление водяных паров, содержащихся в воздухе? Ответ выразить в (кПа).
Решение
Дано:
$T=100°C$
$ϕ_{от}=60%$
$P_{вп}-?$
Решение:
Известно, что для $T=100°C$ давление насыщенного пара $P_*=100$кПа. Тогда $ϕ={P_{вп}}/{P_*}·100⇒P_{вп}=0.6·100=60$кПа.
Ответ: 60
Показать решение
Полный курс
Задача 8
Давление насыщенного водяного пара при 24◦С равно 22,4 мм рт. ст., а при 13◦С — 11,23 мм рт. ст. Определите относительную влажность воздуха при температуре 24◦С, если точка росы равна 13◦С. Ответ выразите в процентах и округлите до целых. Ответ выразите в (%).
Решение
Дано:
$T’=24°C+273=297°C$
$P_{нп}=22.4$мм.рт.ст.
$T_p=13°C+273=286°C$
$P’_{нп}=11.23$мм.рт.ст.
$ϕ_{от}(T=24°C)$
Решение:
$V=const$ (изохорный), тогда: ${P_p^{нп}}/{T_p}={P_{нп}}/{T_1}⇒P_p^{нп}={P’_{нп}·T_p}/{T_1}⇒$ подставим в выражение. Тогда для нахождения $ϕ_{от}:ϕ_{от}={P_p^{нп}}/{P_{нп}}={P’_{нп}·T_p}/{T_1·P_{нп}}={11.23·286}/{297·22.4}=50%$
Ответ: 50
Показать решение
Полный курс
Задача 9
Определите массу воды, взятой при температуре 40◦С, которую нагревают до температуры кипения и полностью испаряют. Необходимая для этих процессов энергия составляет 638 кДж. Ответ выразите в (г).
Решение
Дано:
$m-?$
$T_1=40°$
$Q_{об}=638$кДж
Решение:
$c_вm∆T+r·m=Q_{об}$ – закон теплообмена.
$m={Q_{об}}/{c_в∆T+r}={6.38·10^3}/{4200·60+2.3·10^6}=250$г.
Ответ: 250
Показать решение
Полный курс
Задача 10
Какое количество теплоты необходимо для нагревания железного бруска массой 200 г от 285 К до 305 К? Ответ выразите в (Дж). Удельная теплоемкость железа 460 Дж/(кг*К)
Решение
Дано:
$m_ж=0.2кг$
$∆T=20K$
$c_ж=460$ Дж/(кг*К)/
$Q-?$
Решение:
По закону нагревания тела равно $Q=c_ж·m_x·∆T=0.460·10^3·0.2·20=1840$Дж.
Ответ: 1840
Показать решение
Полный курс
Задача 11
Каково давление насыщенного водяного пара при температуре 100◦С? Атмосферное давление принять равным $10^5$ Па. Ответ выразите в (кПа).
Решение
Дано:
$p_{нв}-?$
$T=100°C$
Решение:
По определению давления насыщенного пара при $T=100°C$. Составляет 100кПа.
Ответ: 100
Показать решение
Полный курс
Задача 12
В сосуде с подвижным поршнем находятся вода и её насыщенный пар. Если одновременно увеличить в 2 раза температуру сосуда и его объём, то как увеличится его давление? В ответ запишите: примерно в _ раз(а).
Решение
Объём сосуда не влияет на давление насыщенного пара. Влияние температуры на давление насыщенного пара можно определить по уравнению Менделеева-Клайперона $pV=υRT$. Если температуру увеличить в 2 раза, то и давление увеличится в 2 раза.
Ответ: 2
Показать решение
Полный курс
Задача 13
Относительная влажность воздуха в цилиндре под поршнем равна 40%. Воздух изотермически сжали, уменьшив его объём в три раза. Какова стала относительная влажность воздуха? Ответ выразите в (%).
Решение
Дано:
$ϕ_{отн}=40%$
$T=const$
$V_2
$V_2={V_1}/{3}$
$ϕ_{отн}-?$
Решение:
Насыщенный пар подчиняется уравнению Менделеева-Клайперона: $ϕ={n}/{n_{нп}}·100%; n_{нп}$ – не изменяется ($T=const$)
$n=0.4n_{нп}$, следовательно, уменьшение в 3 раза приведет к увеличению $n=1.2=n_{нп}$, но $n=n_{нп}$ это максимум (насыщенный пар).
Ответ: 100
Показать решение
Полный курс
Задача 14
Относительная влажность водяного пара в сосуде при температуре 100◦С равна 62%. Какова плотность этого пара? Ответ округлите до сотых. Ответ выразить в (кг/м3).
Решение
Дано:
$ϕ_{отн}=62%$
$T=100°C$
$ρ_{вп}-?$
Решение:
Относительная влажность это отношение парциального давления паров воды в газе к равновесному давлению паров при данной температуре $ϕ={p}/{p_{нп}}$. При 100°C давление насыщенных паров равно атмосферному $p_{нп}=10^5$Па, тогда $ρ={p·M}/{R·T}={ϕ·p_{нп}·M}/{R·T}={0.62·10^5·0.018}/{8.31·373}=0.36{кг}/{м^3}$.
Ответ: 0.36
Показать решение
Полный курс
Задача 15
В кубическом метре воздуха в помещении при температуре 20◦С находится 1,12 · 10−2 кг водяных паров. Пользуясь таблицей плотности насыщенных паров воды, определите относительную влажность воздуха. Ответ округлите до целого. Ответ выразите в (%).
| t, ◦ C | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| ρ, г/м3 | 13,6 | 14,5 | 15,4 | 16,3 | 17,3 | 18,3 | 19,4 | 20,6 | 21,8 |
Решение
Дано:
$V=1м^3$
$T=20°C$
$m_{вп}=1.12·10^{-2}$кг
$ϕ_{отн}-?$
Решение:
1) Определим плотность водяных паров в комнате $ρ_{вп}={m_{вп}}/{V}={1.12·10^{-2}}/{1}{кг}/{м^3}$.
2) Используя таблицу, определим, и по при температуре 20°C плотность насыщенных паров равна $ρ_{нп}=1.73·10^{-2}{кг}/{м^3}$.
3) Тогда относительная влажность воздуха в комнате равна $ϕ_{отн}={ρ_{вп}}/{ρ_{нп}}={1.12·10^{-2}}/{1.73·10^{-2}}=100≈65%$.
Ответ: 65
Показать решение
Полный курс
Задача 16
Парциальное давление водяного пара в 1,25 раза меньше, чем давление насыщенного пара при той же температуре. Чему равна относительная влажность воздуха? Ответ выразите в (%).
Решение
Дано:
$p_п=p$
$p_н=1.25p$
$ϕ-?$
Решение:
Относительная влажность воздуха определяется как: $ϕ={p_п}/{p_н}·100%$, где $p_п$ – парциальное давление газа; $p_н$ – давление насыщенного газа при той же температуре, тогда имеем: $ϕ={p_п}/{p_н}·100%={p·100%}/{1.25p}=80%$
Ответ: 80
Показать решение
Полный курс
Задача 17
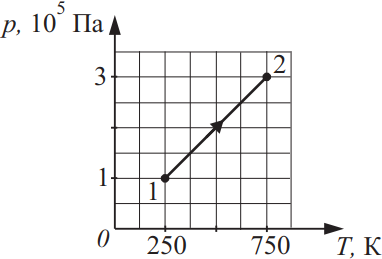
Какое количество теплоты получает 4 моля одноатомного идеального газа в процессе, график которого изображён на рисунке? Ответ выразите в (кДж).
Решение
Дано:
$υ=4$моль
$i=3$
$p_1=10^5$Па
$p_2=3·10^5$Па
$T_1=250K$
$T_2=750K$
$R=8.31{Дж}/{моль·К}$
$Q_{12}-?$
Решение:
Запишем I начало термодинамики: $Q_{12}=A_{12}+∆U_{12}$(1), где $A_{12}=p·∆V$, т.к. $V=const$ (процесс изохорный, то $∆V=0$ и работа газа $A_{12}=0$Дж).
$∆U_{12}={i}/{2}·υ·R∆T={i}/{2}υR(T_2-T_1)$(2) – изменение внутренней энергии газа, где $R$ – универсальная газовая постоянная.
Подставим (2) в (1) и найдем $Q_{12}: Q_{12}={i}/{2}υR(T_2-T_1)$(3)
Подставим числовые значения в (3): $Q_{12}={3}/{2}·4·8.31·(750-250)=24930Дж=24.93кДж$
Ответ: 24.93
Показать решение
Полный курс
Источник
За это задание ты можешь получить 1 балл. Уровень сложности: базовый.
Средний процент выполнения: 72.5%
Ответом к заданию 8 по физике может быть целое число или конечная десятичная дробь.
Задачи для практики
Задача 1
Сосуд вместимостью 12 л, содержащий газ при давлении 0,4 МПа, соединяют с другим сосудом, из которого откачан воздух. Найдите конечное значение давления. Процесс изотермический. Вместимость второго сосуда равна 3,0 л. Ответ выразите в (МПа).
Решение
Дано:
$V_1=12·10^{-3}м^3$
$V_2=3·10^{-3}м^3$
$p_1=0.4·10^6$Па
$T_1=T_2=T=const$
$p_2-?$
Решение:
Из уравнения Менделеева-Клайперона имеем: ${p_1V_1}/{T_1}={p_2(V_2+V_1)}/{T_2}$(1), т.к. $T_1=T_2=T=const$, можно записать: $p_1V_1=p_2(V-2+V_1)$(2), откуда $p_2={p_1V_1}/{(V_2+V_1)}={0.4·10^6·12·10^{-3}}/{15·10^{-3}}=0.32$МПа.
Ответ: 0.32
Показать решение
Полный курс
Задача 2
Газ, занимающий объём 12,32 л, охладили при постоянном давлении на 45 К, после чего его объём стал равен 10,52 л. Какова была первоначальная температура газа? Ответ выразите в (К).
Решение
Дано:
$∆T=45K$
$V_1=12.32·10^{-3}м^3$
$V_2=10.52·10^{-3}м^3$
$p_1=p_2=p=const$
$T_1-?$
Решение:
Из уравнения Менделеева-Клайперона имеем: ${p_1V_1}/{T_1}={p_2V_2}/{T_2}$(1), учитывая, что $p=const$, имеем: ${pV_1}/{T_1}={pV_2}/{T_2}$ или $V_1T_2=V_2T_1$(2). Так как газ охладили, то $T_2=T_1-∆T$(3). Подставим (3) в (2): $V_1T_1-V_1∆T=V_2T_1⇒T_1={V_1∆T}/{(V_1-V_2)}={12.32·10^{-3}·45}/{1.8·10^{-3}}=308K$.
Ответ: 308
Показать решение
Полный курс
Задача 3
В закрытом сосуде находится 120 г газа при комнатной температуре. Какая масса газа вытечет из сосуда, если после открытия крана давление в сосуде понизится в 4 раза? Ответ выразите в (кг).
Решение
Дано:
$T=20+273=293К$
$P_2={P_1}/{4}$
$m_1=0.12$кг
$∆m-?$
$T=const$
$V=const$
Решение:
Зная уравнение Менделеева-Клайперона составим систему 1 и 2.
${tableP_1V={m}/{M}·RT_1; P_2V={m}/{M}·RT_2;$, то $4={m_1}/{m_2}; m_2=0.03$.
$∆m=m_1-m_2=0.12-0.03=0.09$кг.
Ответ: 0.09
Показать решение
Полный курс
Задача 4
В сосуде содержится неон при температуре −3◦С. Во сколько раз увеличится средняя кинетическая энергия теплового движения молекул неона, если его нагреть до 132◦С? В ответе запишите в(во) сколько раз(а).
Решение
Дано:
$t_1=-3+273=270К$
$T_2=132+273=405K$
${E_{к_2}}/{E_{к_1}}$
Решение:
$E_к={3}/{2}KT$.
${E_{к_2}}/{E_{к_1}}={T_2}/{T_1}={405}/{270}=1.5$
Ответ: 1.5
Показать решение
Полный курс
Задача 5
В сосуде содержится аргон при температуре 327◦С. Какая абсолютная температура установится, если концентрацию аргона увеличить в 2 раза, а давление уменьшить в 3 раза? Ответ выразить в (K).
Решение
Дано:
$T^1_{Ар}=327+273=600K$
$n_2=2·n_1$
$P_2={P_1}/{3}$
$T_2$
Решение:
Запишем уравнение состояния газа дважды:
${tableP_1=n_1·K·T_1; P_2=n_2·K·T_2;$ $⇒T_2={T_1}/{2}={600}/{6}=100K$.
Ответ: 100
Показать решение
Полный курс
Задача 6
В сосуде содержится водород, манометр показывает 0,5 атмосферы. Какое установится давление, если концентрацию водорода увеличить в 6 раз, а среднюю кинетическую энергию теплового движения его молекул уменьшить в 4 раза? Ответ выразите в (кПа).
Решение
Дано:
$P_1=0.5·P_{атм}$
$n_2=6·n_1$
$E_{к_2}={E_{к_1}}/{4}$
$P_{атм}=10^5$
Решение:
${tableP_1={2}/{3}·n_1·E_{к_1}; P_2={2}/{3}·n_2·E_{к_2};$ $⇒{0.5·10^5}/{P_2}={1}/{6}:{1}/{4}$.
Для 1 и 2 случая $P_2=75·10^3$Па.
Ответ: 75
Показать решение
Полный курс
Задача 7
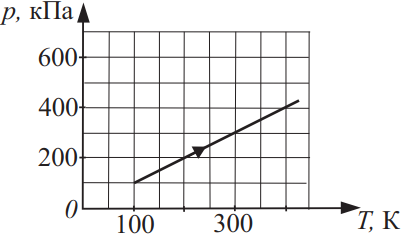
На рисунке показан график изменения давления 10 моль газа при изохорном нагревании. Найдите объём этого газа. Ответ округлите до целого, выразив в (дм3).
Решение
Дано:
$V-?$
$V=const$
$υ=10$моль
Решение:
Из уравнения Менделеева-Клайперона $pV=υRT⇒V={υRT}/{p}={10·8.31·100}/{100·10^3}=83.1дм^3$
Ответ: 83
Показать решение
Полный курс
Задача 8
1 моль идеального газа изохорно охлаждают на 200 К, при этом его давление уменьшается в 3 раза. Найдите первоначальную температуру газа. Ответ выразите в (К).
Решение
Дано:
$υ=1$моль
$υ=const$
$∆T=200K$
${P_1}/{3}=P_2$
$T_0-?$
Решение:
${P_1}/{T_1} > {P_2}/{T_2}$ – изохорный.
$T_0={P_1}/{P_2}·T_2=3(1-200)$
$2T_0=600$
$T_0=300K$
Ответ: 300
Показать решение
Полный курс
Задача 9
Определите плотность азота при температуре 27◦С и давлении 150 кПа. Ответ округлите до десятых. Ответ выразите в (кг/м3).
Решение
Дано:
$T=27°C=300K$
$P=150$кПа
$v=2(Т_2)$
$ρ-?$
Решение:
$PV={m}/{M}·RT$
$ρ·R·T=P·M$
$ρ={P·M}/{R·T}={150·10^3·0.028}/{8.31·300}=1.7{кг}/м^3$.
Ответ: 1.7
Показать решение
Полный курс
Задача 10
Определите температуру азота, имеющего массу 4 г, занимающего объём 831 см3 при давлении 0,2 МПа. Ответ выразите в (К).
Решение
Дано:
$N_2T-?$
$m=4·10^{-3}кг$
$V=831см^3$
$P=0.2·10^6$
$T_?$
Решение:
По закону Менделеева-Клайперона $pV={m}/{M}R·T; T={pv·M}/{m·R}$
$T={0.2·10^6·8.31·0.028}/{4·10^{-3}·8.31}=140K$
Ответ: 140
Показать решение
Полный курс
Задача 11
При повышении температуры идеального газа на 100 К среднеквадратичная скорость движения молекул выросла с 200 м/с до 600 м/с. Насколько надо понизить температуру газа, чтобы среднеквадратичная скорость уменьшилась с 600 м/с до 400 м/с? В ответе запишите на сколько (K).
Решение
Дано:
$∆T=100K↑$
$υ_{cр_1}=200$м/с
$υ_{cр_2}=600$м/с
$∆T-?↓$
$υ_{cр_2}=600$м/с
$υ_{cр_3}=400$м/с
Решение:
В первом процессе $T_1={υ_1^2μ}/{3R}$
$T_2={υ_2^2μ}/{3R}$
$∆T_1=T_2-T_1={μ}/{3R}·(υ_2^2·r_1^2)$
${μ}/{3R}={∆T}/{υ_2^2-r_1^2}={1}/{3200}$
Тогда $∆T_2={μ}/{3R}(υ_2^2-υ_3^2)={1}/{3200}(400^2-600^2)=62.5K$
Ответ: 62.5
Показать решение
Полный курс
Задача 12
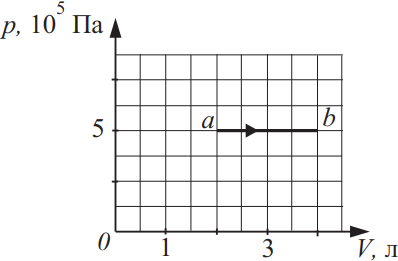
Идеальный газ в количестве 1,5 моль совершает процесс, изображённый на рисунке. Какова температура газа в состоянии b? Ответ выразите в (K), округлив до сотых.
Решение
Дано:
$v=1.5$моль
$T_в-?$
$P=const=10^5$Па
$V_a=2л$
$V_в=4л$
Решение:
По закону Менделеева-Клайперона для точки а и в составим систему: ${tableP·V_a=vRT_a(1); P·V_в=vRT_в(2);$. Из (2) найдем: $T_в={5·10^5·4·10^{-3}}/{1.5·8.31}=160.45K$
Ответ: 160.45
Показать решение
Полный курс
Задача 13
Концентрация молекул идеального одноатомного газа равна 2 · 1024 м−3. Какое давление оказывает газ на стенки сосуда, если при этом средняя кинетическая энергия молекулы равна 1,5 · 10−20 Дж? Ответ выразите в (кПа).
Решение
Дано:
$n=2·10^{24}м^{-3}$
$E_к=1.5·10^{-20}$
$P-?$
Решение:
${tableE_к={3}/{2}KT={3}/{2}K{P}/{nK}; P=nKT;$
Выразим и получим формулу из основ МКТ: $p={E_к·2n}/{3}={1.5·10^{-20}·2·2·10^{24}}/{3}=20$кПа.
Ответ: 20
Показать решение
Полный курс
Задача 14
Температура идеального газа понизилась от 700◦С до 350◦С. Во сколько раз при этом изменилась средняя кинетическая энергия движения молекул газа? Ответ округлить до сотых
Решение
Дано:
$T_1=700°C+273=973K$
$T_2=350°C+273=623K$
${E_1}/{E_2}-?$
Решение:
Из основ молекулярно-кинетической теории известно, что ${E_1}/{E_2}={T_1}/{T_2}$
${E_1}/{E_2}={973}/{623}=1.56$
Ответ: 1.56
Показать решение
Полный курс
Задача 15

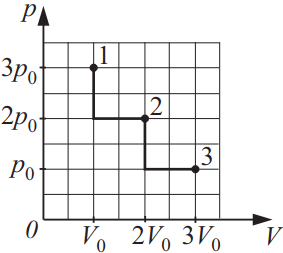
На диаграмме pV изображены процессы перевода некоторой неизменной массы идеального газа из состояния 1 в состояние 3. Начальная (T1) и конечная (T3) температуры связаны между собой соотношением T3/T1…
Решение
Дано:
$Т_1-$начальная
$Т_2$конечная
${T_3}/{T_1}-?$
Решение:
Запишем уравнение Менделеева-Клайперона для начальной и конечной точки состояния: ${table.{p_1·V_1}/{T_1}=υR; .{p_3·V_3}/{T_3}=υR;$.
$⇒{p_1·V_1}/{T_1}={p_3·V_3}/{T_3}⇒{T_3}/{T_1}={p_3·V_3}/{p_1·V_1}⇒{T_3}/{T_1}={p_0·3V_0}/{3p_0·V_0}=1$.
Ответ: 1
Показать решение
Полный курс
Задача 16
При какой температуре молекулы гелия имеют такую же среднюю квадратичную скорость, как молекулы водорода при 27◦С? Ответ выразите в (◦ С).
Решение
Дано:
$t_{H_2}=27°C$
$_{He}=_{H_2}$
$t_{He}-?$
Решение:
Средняя квадратичная скорость молекул гелия и водорода ($He$ и $H_2$) равны соответственно: $_{He}=√{{3RT_{He}}/{μ_{He}}}$, где $T_{He}=t_{He}+273°C$
$_{H_2}=√{{3RT_{H_2}}/{μ_{H_2}}}$, где $T_{H_2}=t_{H_2}-273°C$
Молярные массы гелия $He$ и водорода $H_2$ равны соответственно: $μ_{He}=4·10^{-3}кг/моль; μ_{H_2}=2·10^{-3}кг/моль; T_{H_2}=27°C+273°C=300K$
$√{{3RT_{He}}/{μ_{He}}}=√{{3RT_{H_2}}/{μ_{H_2}}}⇒{3RT_{He}}/{μ_{He}}={3RT_{H_2}}/{μ_{H_2}}⇒T_{He}={T_{H_2}·μ_{He}}/{μ_{H_2}}={300·4·10^{-3}}/{2·10^{-3}}=600K$, тогда $t_{He}=T_{He}-273°C=600°C-273°C=327°C$
Ответ: 327
Показать решение
Полный курс
Задача 17
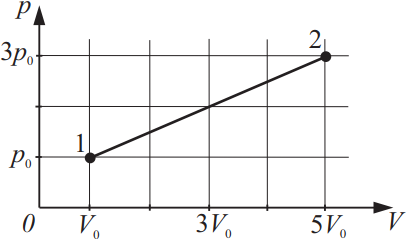
На рисунке изображено изменение состояния идеального газа. Во сколько раз температура в состоянии 2 больше, чем температура в состоянии 1?
Решение
Дано:
$p_1=p_0$
$V_1=V_0$
$p_2=3p_0$
$V_2=5V_0$
${T_2}/{T_1}-?$
Решение:
Из уравнения Менделеева-Клайперона: $pV={m}/{μ}RT$(1), следует равенство ${p_1V_1}/{T_1}={p_2V_2}/{T_2}⇒{p_0V_0}/{T_1}={3p_0·5V_0}/{T_2}$(2).
Из (2) имеем: $p_0V_0T_2=3p_0V_0·5T_1$
$T_2=3·5T_1⇒T_2=15T_1$ или ${T_2}/{T_1}=15$
Ответ: 15
Показать решение
Полный курс
Источник
