Вращательное движение сосуда с жидкостью
МОУ «Сернурская средняя общеобразовательная школа №2» имени Н.А.Заболоцкого
Исследовательская работа
на тему:
Изучение закономерностей вращательного движения на примере вращающегося сосуда с жидкостью
Выполнил:
Шабалин А.
Ученик
10«Б» класса
Руководитель:
Онучина В.И.
Сернур 2014
Содержание
- Введение
Цели и задачи
- Основная часть:
- Теоретическая часть
- Практическая часть:
Опыт №1
Опыт №2
Опыт №3
- Заключение
- Список используемой литературы
Введение.
Читая газеты, нередко можно встретить сообщения о трагедиях, разыгрывающихся в разных частях света по вине разбушевавшегося Великого Невидимого. Ураганы, тайфуны, торнадо, смерчи — эти опасные явления природы причиняют немало бед человеку.
В истории развития человеческого общества можно найти много примеров того, как по «воле» ветра и воды оказывались опустошенными обширные районы земного шара. При этом число человеческих жертв достигало сотен и тысяч человек.
Время от времени в атмосфере зарождаются и развиваются грандиозные вихри, вовлекающие в сферу своей деятельности огромные массы воздуха. Это тайфуны и ураганы. Закрутившись в гигантские спирали, они путешествуют по планете.
Сведения об очень сильных ураганах, случившихся в далеком прошлом, дошли до нашего времени в разных литературных источниках. К древнейшему из них относится шумеро-вавилонское сказание о всемирном потопе. Там рассказывается о страшном урагане, бушевавшем семь дней и ночей, и о ливне, затопившем Землю и погубившем всё.
Цели и задачи
Цели:
- Провести эксперименты с вращающейся жидкостью
- Получить уравнение поверхности вращающейся жидкости
Задачи:
- Изучить литературу по вращательному движению жидкости и газа, изучить применение этого явления в природе и технике
- Провести эксперименты : вращение жидкости с маком, вращение жидкости на приборе вращательное движение
- Построить уравнение этой поверхности жидкости в координатах х;у
- Сделать выводы
Теоретическая часть
Известен исторический мысленный эксперимент Ньютона с вращением жидкости в цилиндрическом ведре с получением поверхности в виде параболоида вращения. При проведении опыта можно провести аналогию между движением фрагмента вращающейся жидкости на ее поверхности, движущейся под действием выталкивающей силы и силы тяжести , и движением шара на нити, вращающимся в горизонтальной плоскости и движущимся под действием силы натяжения и силы тяжести. Очень часто для объяснения формы поверхности жидкости используют вращающуюся систему отсчета, в которой возникает «центробежная сила инерции». Однако придерживаясь механики Ньютона мы не должны вводить сил, не связанных с воздействием каких-либо тел. Сила инерции – это удобный математический трюк, который можно ввести рассмотрев несколько случаев сопоставления описания движений в инерциальной и неинерциальной системе отсчета и показав, что математически можно вводить в уравнения Ньютона некую псевдосилу. Возможность получения параболы в сечении вращающегося плоского слоя можно показать и в инерциальной системе отсчета.
Рассмотрим жидкость, вращающуюся вместе с сосудом с угловой скоростью ω вокруг вертикальной оси ОУ, инерциальной системы отсчета
Условие равновесия относительно остальной жидкости вертикального столбика жидкости высотой АВ=у, находящегося на расстоянии х от оси вращения запишется как
-mg-p₀ ΔЅ+p₁ΔЅ=0
Где ΔЅ – площадь основания узкого столбика, m=ρу ΔЅ – масса столбика, p₀ – атмосферное давление, p₁ – давление у основания столбика. Тогда
ρgyΔЅ=(p₁-p₀)ΔЅ
и
p₁-p₀=ρgy (1)
Согласно закону Паскаля давление p₁ характеризует силу воздействия жидкости в окрестности точки А как на вертикальный столб АВ снизу, так и на горизонтальный столб АО слева. Поэтому для определения p₁ рассмотрим движение горизонтального столбика ОА того же поперечного сечения ΔЅ, вращающегося вокруг оси ОУ. Он вращается как твердое дело. Если горизонтальный столбик ОА разбить на N элементарных фрагментов толщиной Δх, расположенный на расстоянии х ̨ то для каждого из них выполнено уравнение
Δmω²x ̨=(p ̨₊₁-p ̨)ΔЅ
Находим сумму N уравнений, в левой части получим значение Mω²(х/2) (удобнее сначала суммировать первые и последнее, второе и предпоследнее слагаемые с получением одинакового результата Δmω²x от каждой пары, а затем сложить N/2 одинаковых слагаемых). В первой части после суммирования останутся два слагаемых, содержащие давление в начале горизонтального столба p₀ и давление у торца на расстоянии х, т.е. p₁. Таким можно получить
ΔmNω²x/2=(p₁−p₀) (2)
С учетом того, что ΔmN = Mₓ=ρΔЅx – масса столба ОА с длиной х и площадью сечения ΔЅ , а давление в точке А уже было выражено через высоту столба АВ, из уравнений (1) и (2) получаем соотношение между у и х.
ρΔЅxω²x/2=ρgy
ω²x/2=gy
y= (3).
Кривая у(х) в сечении жидкости плоскостью ОХУ описывается функцией у(х)= , графиком которого является парабола с вершиной в точке О.
Следовательно, поверхность жидкости является поверхностью, образованной вращением параболы вокруг оси ОУ.
Практическая часть
Опыт №1
Цель опыта: Иллюстрация закономерностей вращательного движения на примере вращающегося
- Основание
- Узел привода с рамкой и датчиком частоты вращения
- Кювета
- Кабель измерительный
- Компьютерный измерительный блог
- Источник постоянного тока напряжения не более 15 В
Подготовка установки
Установите на демонстрационный стол основание и зажмите в нем узел привода с рамкой и датчиком частоты вращения. Подключите кабель питания электродвигателя к Блоку питания регулируемому (стабилированный выход 15В). Включите разъем кабеля датчика угловой скорости в разъем на корпусе привода. Подключите датчик к компьютеру. Проверьте, чтобы в зоне вращения рамы не осталось никаких посторонних предметов
Установите кювету на нижнем или верхнем профиле рамы. Кювета может быть установлена симметрично относительно оси вращения или сдвинута таким образом, чтобы ось вращения проходила через боковую стенку. На одной из стенок кюветы имеется изображение параболы. Кривую именно этого вида образует поверхность вращающейся жидкости, если рассечь(или ограничить) ее плоскость ю, проходящей через ось вращения. Парабола нанесена для симметричного расположения кюветы, поэтому такое расположение кюветы рекомендуется в качестве основного при проведении данного опыта.
Выполнение опыта:
Включите компьютер и запустите программу «Цифровая лаборатория. Демонстрационные эксперименты». В разделе «Физика» выберите группу экспериментов «Вращательное движение», в которой, в свою очередь, войдите в сценарий «Определение угловой скорости», где по умолчанию измеряется частота вращения.
Наполните кювету подкрашенной водой (например, ярко окрашенным газированным напитком). Для того, чтобы профиль поверхности полностью совпал с параболой на стенке кюветы, в нее необходимо налить 150мл жидкости.
Убедитесь, что ручка плавной регулировки напряжения блока питания находится в крайнем левом положении (минимальное напряжение). Включите блок питания и плавно повышайте угловую скорость, наблюдая за изменением распределения жидкости по объему кюветы и формой ее поверхности.
Прекратите изменение частоты вращения, когда поверхность жидкости совпадает с нарисованной на кювете параболой, чтобы ученики могли убедиться в том, что разрез жидкости – парабола. Остановите вращение рамы.
Опыт №2
Когда я смотрел фильм «Охотники за торнадо», то понял, какое это опасное явление. Раз в воздух взлетают автомобили, сходят с рельсов поезда и разваливаются дома, у мягкого и невидимого воздуха обнаруживается такая мощь, что не каждому снаряду под силу. Поэтому дома провести опыты по моделированию вихрей трудно. Но в книжке о простых домашних опытах я прочитал, что потоки воздуха и потоки воды очень похожи. Тогда я решил попробовать испытать способна ли вода перемещать предметы, которые в воде тонут.
Сначала я задумался о способе заставить воду вращаться. Стеклянная банка не дает воде разлетаться в стороны при вращении. Обычный шуруповёрт создает вращение, которое он передает воде через весло, вставленное вместо сверла. Вот и вся моя научная установка.
Чтобы сделать движение воды видимым, насыпаем в воду семена пищевого мака. Они мелкие, но тонут в воде. Начало опыта показано на снимке.
Включаем наш шуруповёрт. Весло вращается, закручивая воду. Обороты нарастают, и потоки воды поднимают семена на поверхность. А на поверхности образуется воронка.
Снимок очень похож на картинку смерча: вверху черная туча и воронкообразный вихрь.
Через две минуты вода растрачивает полученную при закрутке энергию. Скорость вращения уменьшается, и тяжелые частицы постепенно идут вниз.
Последний снимок показывает, что оседающие маковки похожи на маленький вулкан с кратером посередине. Но силы воды на исходе, и вулкан превращается в холмик с округлыми краями.
Опыт №3
Вращение газированной воды
Опыт №4
Вливание во вращающуюся горячую воду холодной воды
Заключение
В ходе моей работы установлено, что поверхность вращающей жидкости представляет собой форму параболы.
При вращении воды с семенами мака, при увеличении оборотов вращения, мак всплывает на поверхность.
При вращении воды с газом, поверхность вращающейся жидкости так же представляет собой параболу.
При вливании во вращающуюся горячую воду холодной, потоки холодной воды опускаются вниз и поднимаются по краю.
Список используемой литературы
- Бакулин П.И., Кононович Э.В., Мороз В.И. Курс общей астрономии, М., Наука, 1983.
- Косинов Н.В. Физический вакуум и гравитация. Физический вакуум и природа, N4, 2000, с.55 – 58.
- А.В.Бялко. Наша планета – Земля. Библиотечка “Кванта” вып. 29, М., Наука, 1989.
- Р.Скорер. Аэрогидродинамика окружающей среды, М., Мир, 1980.
Источник
Возьмем открытый цилиндрический сосуд с жидкостью и сообщим ему постоянную угловую скорость w вращения вокруг вертикальной оси. Жидкость постепенно приобретет ту же угловую скорость, что и сосуд, а свободная поверхность ее видоизменится: в центральной части уровень жидкости понизится, у стенок – повысится, и вся свободная поверхность жидкости станет некоторой поверхностью вращения (рис. 2.11).
На жидкость в этом случае будут действовать две массовые силы, сила тяжести и центробежная сила, которые, будучи отнесенными к единице массы, соответственно равны g и w2r. Равнодействующая массовая сила j увеличивается с увеличением радиуса за счет второй составляющей, а угол наклона ее к горизонту уменьшается. Эта сила нормальна к свободной поверхности жидкости, поэтому угол наклона поверхности к горизонту возрастает с увеличением радиуса. Найдем уравнение положения свободной поверхности.
Рис. 2.11
Учитывая, что сила j нормальна к свободной поверхности, получим
отсюда
или после интегрирования
В точке пересечения свободной поверхности с осью вращения C = h, поэтому окончательно будем иметь
(2.10)
т. е. свободная поверхность жидкости является параболоидом вращения.
Максимальную высоту подъема жидкости можно определить исходя из равенства объемов неподвижной жидкости и жидкости во время вращения.
На практике очень часто приходится иметь дело с вращением сосуда, заполненного жидкостью, вокруг горизонтальной оси. При этом угловая скорость w столь велика, что сила тяжести на порядок меньше центробежных сил, и ее действие можно не учитывать. Закон изменения давления в жидкости для этого случая получим из рассмотрения уравнения равновесия элементарного объема с площадью основания dS и высотой dr, взятой вдоль радиуса (рис. 2.12). На выделенный элемент жидкости действуют силы давления и центробежная сила.
Обозначив давление в центре площадки dS, расположенной на радиусе r, через p, а в центре другого основания объема (на радиусе r + dr) через p + dp, получим следующее уравнение равновесия выделенного объема в направлении радиуса
или
Рис. 2.12
После интегрирования
Постоянную C найдем из условия, что при r = r0 p = p0.
Следовательно
Подставив ее значение в предыдущее уравнение, получим связь между p и r в следующем виде:
(2.11)
Очевидно, что поверхностями уровня в данном случае будут цилиндрические поверхности с общей осью – осью вращения жидкости.
Часто бывает необходимо определить силу давления вращающейся вместе с сосудом жидкости на его стенку, нормальную к его оси вращения. Для этого определим силу давления, приходящуюся на элементарную кольцевую площадку радиусом r и шириной dr. Используя формулу (2.11), получим
а затем следует выполнить интегрирование в требуемых пределах.
При большой скорости вращения жидкости получается значительная суммарная сила давления на стенку. Это используется в некоторых фрикционных муфтах, где для сцепления двух валов требуется создание больших сил давления.
Источник
Вращение сосуда с жидкостью вокруг вертикальной оси
Возьмем открытый цилиндрический сосуд с жидкостью и сообщим ему постоянную угловую скорость w вращения вокруг вертикальной оси. Жидкость постепенно приобретет ту же угловую скорость, что и сосуд, а свободная поверхность ее видоизменится: в центральной части уровень жидкости понизится, у стенок – повысится, и вся свободная поверхность жидкости станет некоторой поверхностью вращения (рис. 2.15).
Рис. 2.15
На жидкость в этом случае будут действовать две массовые силы, сила тяжести и центробежная сила, которые, будучи отнесенными к единице массы, соответственно равны g и . Равнодействующая массовая сила j увеличивается с увеличением радиуса за счет второй составляющей, а угол наклона ее к горизонту уменьшается. Эта сила нормальна к свободной поверхности жидкости, поэтому угол наклона поверхности к горизонту возрастает с увеличением радиуса. Найдем уравнение положения свободной поверхности.
Учитывая, что сила нормальна к свободной поверхности, получим , отсюда или после интегрирования .
В точке пересечения свободной поверхности с осью вращения C=h и r=0, поэтому окончательно будем иметь
, (2.10)
где .
Таким образом, свободная поверхность жидкости является параболоидом вращения. Максимальную высоту подъема жидкости можно определить, используя выражение (2.10) и исходя из равенства объемов неподвижной жидкости и жидкости во время вращения.
Запишем закон изменения давления во вращающейся жидкости в функции радиуса и глубины относительно верхней точки жидкости (без вывода):
.
Вращение сосуда с жидкостью вокруг горизонтальной оси
При таком вращении угловая скорость w столь велика, что (действие силы тяжести можно не учитывать). Закон изменения давления в жидкости для этого случая получим из рассмотрения уравнения равновесия элементарного объема с площадью основания dS и высотой dr, взятой вдоль радиуса (рис. 2.16). На выделенный элемент жидкости действуют силы давления и центробежная сила.
Рис. 2.16
Обозначив давление в центре площадки dS, расположенной на радиусе r, через p, а в центре другого основания объема (на радиусе r + dr) через p + dp (разложили p в ряд Тейлора, но так как в данном случае p зависит только от r, то dr/dr сократился), получим следующее уравнение равновесия выделенного объема в направлении радиуса
или .
После интегрирования получим . Постоянную C найдем из условия, что при r = rp = p0, следовательно, .
Подставив ее значение в предыдущее уравнение, получим связь между p и r в следующем виде:
. (2.11)
Очевидно, что поверхностями уровня в данном случае будут цилиндрические поверхности с общей осью – осью вращения жидкости.
Часто бывает необходимо определить силу давления вращающейся вместе с сосудом жидкости на его стенку, нормальную к его оси вращения. Для этого определим силу давления, приходящуюся на элементарную кольцевую площадку радиусом r и шириной dr. Используя формулу (2.11), получим
,
а затем следует выполнить интегрирование в требуемых пределах:
.
Если равно внешнему давлению, то .
При большой скорости вращения жидкости получается значительная суммарная сила давления Fб на боковую стенку. Это используется в некоторых фрикционных муфтах, где для сцепления двух валов требуется создание больших сил давления.
Приведем выражение для определения силы Fб без вывода:
, где – длина цилиндра.
Источник
Возьмем открытый цилиндрический сосуд
с жидкостью и сообщим ему вращение с
постоянной угловой скоростью ω вокруг
его вертикальной оси. Силы трения о
стенки вращающегося сосуда будут
увлекать за собой жидкость. Она постепенно
приобретет ту же угловую скорость, что
и сосуд, находясь по отношению к сосуду
в покое. Свободная поверхность жидкости
изменится.
В центральной части уровень жидкости
опустится, у стенок она поднимется, и
вся свободная поверхность жидкости
станет поверхностью вращения (рис.4.6).
На жидкость будут действовать силы
давления, силы тяжести и силы инерции
переносного движения. Частица жидкости
будет находиться под действием ускорения
силы тяжести и центростремительного
ускорения, а равное ему ускорение силы
инерции будет центробежным. Единичная
массовая сила тяжести Fg
= gи единичная
массовая центробежная силаFцб
= ω2r.
Проекции этих сил на оси координат дадут
следующие выражения
X = (V2/r)Cos(r^x) = ω2r
Cos(r^x)= ω2X
Y = (V2/r)Cos(r^y) = ω2r
Cos(r^у)= ω2Y,
Z = -g

Подставляя эти проекции в дифференциальное
уравнение поверхности равного давления
и интегрируя :
X*dх+У*dy+Z*dz
= 0,
получим ρ(ω2/2)
(X2
+ Y2)
– ρgz
+ С=
0.
Уравнение свободной
поверхности, например, получим, при
нулевых условиях: Р
= const,
х = у = 0,
z= z,где
координата вершины параболоида свободной
поверхности. ТогдаС
=ρgz.
ρ(ω2/2)
(X2
+ Y2)
– ρgz
+ ρgz
= 0,
(ω2/2)
(X2
+ Y2)
=g(z
– z)
и после деления на g
уравнение свободной поверхности
получит вид
![]()
(4.22)
Таким образом, поверхности равного
давления, в том числе и свободная
поверхность, образуют семейство
параболоидов, сдвинутых вдоль вертикальной
оси. Каждому значению рсоответствует свой параболоид, положение
которого определяет константа С.
Эти поверхности будут
конгруэнтными параболоидами вращения
с осью Oz.
Один из этих параболоидов – свободная
поверхность жидкости, где Р=
Ратм.
Две геометрические фигуры
называются конгруэнтными, если их можно
совместить одну с другой, изменив их
положение в пространстве.
Подставляя проекции массовых сил в
дифференциал давления
dp= ρ(Xdx
+ Ydy
+ Zdz),
получим dp= ρω2
(Xdx
+ Ydy)
–ρgdz,
вынесем знак дифференциала за скобки,
dp= ρd[(ω2/2)
(X2
+ Y2)]
–ρgdz,
и проинтегрировав, получим выражение
для определения давления в любой точке
p= ρ(ω2/2)
(X2
+ Y2)
–ρgz
+ С1,
(4.21)
Значение константы для
свободной поверхности
Р = Р,
x=y=0,
z
= z:
С1
= Р
+ ρgz0.
Получим уравнение для определения
давления в любой точке:
![]()
(4.22)
Пользуясь этими уравнениями можно
определить положение свободной
поверхности и давление в сосуде.
Максимальная высота Н подъема жидкости
в параболоиде со свободной поверхностью
может быть определена, следующим образом.
![]()
На практике часто рассматривается
вращение сосуда с жидкостью, когда
угловая скорость ω столь велика, что
силой тяжести можно пренебречь по
сравнению с центробежными силами. При
этом закон изменения давления в жидкости
легко получить из формулы (4.22), в которой
следует принять g(z
– z)= 0.
Поверхности уровня примут вид цилиндров
с общей осью – осью вращения сосуда.
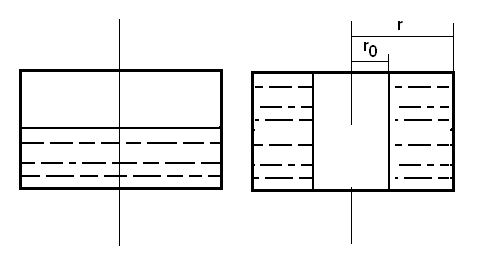
Если сосуд не был заполнен перед началом
вращения, давление Рбудет действовать не в центре, а приr
= r,
вместо выражения (4.22) будем иметь
Р = Р + ρ ω2
(r —r2)/2g,(4.23)
Часто бывает необходимо определить
силу давления вращающейся вместе с
сосудом жидкости на его стенку, нормальную
к оси вращения (или на кольцевую часть
этой стенки).
Для этого необходимо выразить сначала
силу давления, приходящуюся на элементарную
кольцевую площадкуdS
=2πrdrрадиусомrи ширинойdr;

Уравнение, выражающее величину давления
имеет вид
![]()
При определении давления
на верхнюю крышку где Z=0,
Z0
может быть больше нуля Z0>0![]() ,
,
равно нулю![]() и
и
меньше нуля
![]()
В первом случае
![]()
а затем выполнить интегрирование в
требуемых пределах.
При большой угловой скорости жидкости
можно получить весьма значительную
суммарную силу давления на стенку. Этот
эффект используется в некоторых
фрикционных муфтах, где для осуществления
сцепления двух валов требуется создание
больших сил нормального давления.
Способ, указанный выше, применяют для
определения силы осевого давления
жидкости на рабочие колеса центробежных
насосов, а также на крышки центрифуг.
5-я лекция.
Соседние файлы в папке Лекции и семинары
- #
- #
- #
Источник
