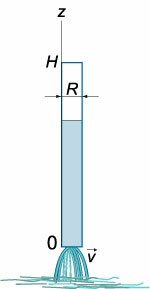
Время за которое вода вытечет из сосуда
Закон Торричелли
Итальянский ученый Эванджелиста Торричелли, изучавший движение жидкостей,
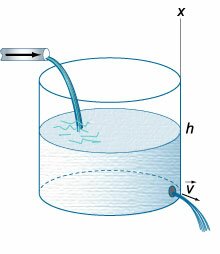
в (1643) году экспериментально обнаружил, что скорость вытекания жидкости через малое отверстие на дне открытого сосуда (рисунок (1)) описывается формулой:
[v = sqrt {2gh} ,]
где (h) − высота уровня жидкости над отверстием, (g) − гравитационная постоянная.
| |
Рис.1 | Рис.2 |
Такая же формула описывает скорость тела, свободного падающего с высоты (h) в поле тяжести Земли в вакууме.
В действительности, найденная формула не совсем точна. В более точном приближении скорость жидкости зависит от формы и размера отверстия, от вязкости жидкости и режима течения. Поэтому,
формула Торричелли часто записывается с дополнительным множителем (varphi:)
[v = varphisqrt {2gh} ,]
где коэффициент (varphi) близок к (1.) Значения параметра (varphi) для отверстий различной формы и размера можно найти в гидравлических справочниках.
Вытекание жидкости из тонкой трубки
Вытекание жидкости из тонкой длинной трубки (рисунок (2)) имеет ряд особенностей. Здесь важную роль играют капиллярные эффекты, обусловленные
поверхностным натяжением и смачиванием вследствие контакта со стенками трубки.
Скорость вытекания жидкости из капиллярных трубок приблизительно пропорциональна высоте столба жидкости над отверстием, то есть
[v = kh,]
где (k) − некоторая константа, зависящая от вязкости жидкости, геометрии и материала трубки.
Далее мы будем описывать вытекание жидкости с помощью дифференциальных уравнений из сосудов обоих типов (широкого и тонкого).
Дифференциальное уравнение вытекания жидкости
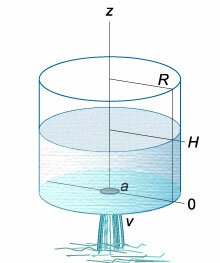
Данное дифференциальное уравнение можно вывести, рассматривая баланс жидкости в сосуде. Возьмем, например, цилиндрический сосуд с широким основанием, радиус
которого равен (R.) Предположим, что жидкость вытекает через малое отверстие радиуса (a) на дне сосуда (рисунок (3)).
|
|
Рис.3 | Рис.4 |
Скорость жидкости описывается формулой Торричелли:
[v = sqrt {2gz} ,]
где (z) − высота жидкости над отверстием. Тогда поток жидкости определяется выражением:
[q = – pi {a^2}sqrt {2gz} .]
Здесь (pi {a^2}) соответствует площади отверстия, через которое вытекает жидкость, а знак “минус” означает,
что уровень жидкости уменьшается по мере ее вытекания из резервуара.
Уравнение баланса жидкости в резервуаре описывается следующим образом:
[frac{{dV}}{{dt}} = q.]
Поскольку изменение объема (dV) можно выразить как
[dV = Sleft( z right)dz,]
то мы получаем дифференциальное уравнение
[frac{{Sleft( z right)dz}}{{dt}} = qleft( z right).]
Подставим функцию (qleft( z right)) в это уравнение:
[frac{{Sleft( z right)dz}}{{dt}} = – pi {a^2}sqrt {2gz} .]
Поперечное сечение ({Sleft( z right)}) цилиндрического сосуда не зависит от высоты (z) и равно
[Sleft( z right) = pi {R^2},]
где (R) − радиус основания цилиндра. Тогда
[require{cancel}
cancel{pi} {R^2}frac{{dz}}{{dt}} = – cancel{pi} {a^2}sqrt {2gz} .
]
В результате получаем уравнение с разделяющимися переменными:
[frac{{dz}}{{sqrt z }} = – frac{{{a^2}}}{{{R^2}}}sqrt {2g} dt.]
Теперь проинтегрируем полученное уравнение, считая, что начальный уровень жидкости составляет (H,) и за время (T) он уменьшается до (0:)
[
{intlimits_H^0 {frac{{dz}}{{sqrt z }}} = – intlimits_0^T {frac{{{a^2}}}{{{R^2}}}sqrt {2g} dt} ,};;
{Rightarrow 2left[ {left. {left( {sqrt z } right)} right|_H^0} right] = – frac{{{a^2}}}{{{R^2}}}sqrt {2g} left[ {left. {left( t right)} right|_0^T} right],};;
{Rightarrow 2sqrt H = frac{{{a^2}}}{{{R^2}}}sqrt {2g} T,};;
{Rightarrow sqrt {2H} = frac{{{a^2}}}{{{R^2}}}sqrt g T.}
]
Отсюда следует выражение для полного времени вытекания жидкости (T:)
[T = frac{{{R^2}}}{{{a^2}}}sqrt {frac{{2H}}{g}} .]
Интересно, что в предельном случае (a = R) (когда площади отверстия и самого цилиндра равны), полученная
формула преобразуется в известную формулу (T = sqrt {largefrac{{2H}}{g}normalsize}, )
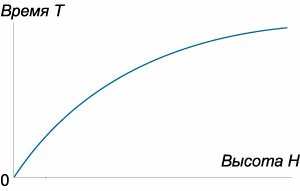
которая определяет время падения материального тела с высоты (H.) Зависимость времени (T) от высоты (H) схематически показана на рисунке (4.)
Аналогично можно описать вытекание жидкости и из сосуда другой формы.
Вывести дифференциальное уравнение вытекания жидкости из конического сосуда и определить полное время вытекания (T.)
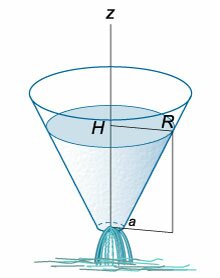
Радиус верхнего основания конического сосуда равен (R,) а радиус нижнего основания (a.) Начальная уровень жидкости составляет (H) (рисунок (5)).
| |
Рис.5 | Рис.6 |
Изменение уровня жидкости на высоте (z) описывается дифференциальным уравнением
[Sleft( z right)frac{{dz}}{{dt}} = qleft( z right),]
где (Sleft( z right)) − площадь поперечного сечения сосуда на высоте (z,) а (qleft( z right)) − поток жидкости, зависящий от высоты (z.)
Принимая во внимание геометрию сосуда, можно предположить, что закон Торричелли выполняется. Поэтому, можно записать:
[qleft( z right) = – pi {a^2}sqrt {2gz} ,]
где (a) − радиус отверстия на дне конического сосуда. Учитывая, что отверстие достаточно малое, осевое сечение можно рассматривать как треугольник
(рисунок (6) выше). Из подобия треугольников следует, что
[frac{R}{H} = frac{r}{z}.]
Следовательно, площадь поверхности жидкости на высоте (z) будет равна
[
{Sleft( z right) = pi {r^2} }
= {pi {left( {frac{{Rz}}{H}} right)^2} }
= {frac{{pi {R^2}{z^2}}}{{{H^2}}}.}
]
Подставляя (Sleft( z right)) и (qleft( z right)) в дифференциальное уравнение, имеем:
[frac{{pi {R^2}{z^2}}}{{{H^2}}}frac{{dz}}{{dt}} = – pi {a^2}sqrt {2gz} .]
После простых преобразований получаем следующее дифференциальное уравнение:
[{z^{largefrac{3}{2}normalsize}}dz = – frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} dt.]
Проинтегрируем обе части, учитывая, что уровень жидкости уменьшается от начального значения (H) до нуля за время (T:)
[
{intlimits_H^0 {{z^{largefrac{3}{2}normalsize}}dz} = – intlimits_0^T {frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} dt} ,};;
{Rightarrow left. {left( {frac{{{z^{largefrac{5}{2}normalsize}}}}{{frac{5}{2}}}} right)} right|_0^H = frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} left[ {left. {left( t right)} right|_0^T} right],};;
{Rightarrow frac{2}{5}{H^{largefrac{5}{2}normalsize}} = frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} T,};;
{Rightarrow frac{1}{5}sqrt {frac{{2H}}{g}} = frac{{{a^2}}}{{{R^2}}}T,};;
{Rightarrow T = frac{{{R^2}}}{{5{a^2}}}sqrt {frac{{2H}}{g}} .}
]
Здесь мы снова видим аналогию с падением материального тела с высоты (H) в гравитационном поле Земли. Как известно,
время падения описывается формулой:
[T = sqrt {frac{{2H}}{g}}. ]
Если мы сравним этот результат со случаем вытекания жидкости из цилиндрического сосуда, то видно, что при тех же самых
значениях (H, R) и (a) время вытекания жидкости из конического сосуда ровно в (5) раз меньше, чем из цилиндра (хотя
объем конического сосуда меньше лишь в (3) раза!). Такие целочисленные отношения в природе выглядят удивительными, не правда ли?
Исследовать вытекание жидкости из тонкой трубки радиусом (R) и высотой (H,) считая трубку полностью заполненной жидкостью.
|
|
Рис.7 | Рис.8 |
Аналогично разобранным выше примерам, мы можем записать уравнение баланса жидкости на некоторой произвольной высоте (z) в следующей форме:
[Sleft( z right)frac{{dz}}{{dt}} = qleft( z right).]
В данном случае площадь поперечного сечения (Sleft( z right)) является константой:
[Sleft( z right) = S = pi {R^2},]
и поток жидкости, вытекающей из сосуда, определяется формулой:
[qleft( z right) = – kz,]
где (k) зависит от размера отверстия, смачиваемости и других параметров.
В результате получаем простое дифференциальное уравнение:
[pi {R^2}frac{{dz}}{{dt}} = – kz,]
или после разделения переменных:
[frac{{dz}}{z} = – frac{k}{{pi {R^2}}}dt.]
Теперь это уравнение можно проинтегрировать, считая, что уровень жидкости уменьшается с высоты (H) до (h) за время от (0) до (t:)
[
{intlimits_H^h {frac{{dz}}{z}} = – intlimits_0^t {frac{k}{{pi {R^2}}}dt} ,};;
{Rightarrow left. {left( {ln z} right)} right|_h^H = frac{k}{{pi {R^2}}}t,};;
{Rightarrow t = frac{{pi {R^2}}}{k}left( {ln H – ln h} right) = frac{{pi {R^2}}}{k}ln frac{H}{h}.}
]
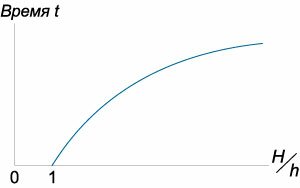
Зависимость времени (t) от отношения (largefrac{H}{h}normalsize) показана схематически на рисунке (8.)
Данная кривая аналогична зависимости времени (T) от высоты (H) для широкого цилиндрического сосуда, для которого справедлив закон Торричелли.
Интересно, что в данной простой модели время вытекания жидкости (t) формально стремится к бесконечности при (h to 0.)
Источник
Рассмотрим бак с водой. В днище бака выполнено отверстие. Задача — рассчитать, как будет выливаться вода из бака, а также проанализировать расчет в Simscape Fluids для применения такого источника жидкости в других схемах. Расчеты по аналитическим формулам для простоты работы с единицами измерения делал в Mathematica. Решение ОДУ расхода и построение графика уровня от времени также выполнено в Mathematica.
Время истечения жидкости — Схема
Схема вот:
Схема для моделирования задачи в Simscape Fluids.
Аналитические расчеты
Характеристики бака и аналитические расчеты:
Характеристики бака и расчеты. Блокнот Mathemetica из двух ячеек (in[11] и in[22]). — диаметр отверстия в баке, — площадь отверстия, — площадь основания бака (бак с прямыми стенками, например — вертикальный цилиндр), — высота уровня воды в баке в начале процесса, — ускорение свободного падения, — плотность воды, — кинематическая вязкость.
— скорость потока через отверстие, вычисляется по формуле Торричелли. В англоязычной литературе, эта формула называется законом Торричелли. Расход — это просто скорость потока , умноженная на площадь отверстия . UnitConvert преобразует единицы расхода в л/мин. Время вытекания воды из бака составило по аналитическим расчетам 1016.8 секунды.
Время истечения жидкости — Модель Simscape Fluids
Теперь, результаты моделирования:
Результаты запуска модели Simscape. Vt — объем воды в баке (л), Q — расход из бака (л/мин).
Результат похож на ожидания. На первом графике отображается объем воды в баке. Первоначальный объем равен 125 л, согласно геометрии бака и высоте уровня. По истечении почти 1000 секунд времени, бак опустошится . Расход остается ненулевым даже при нулевом объеме ввиду специфики математической модели бака. На верхнем графике можно заметить даже отрицательный объем. Стоит учитывать это обстоятельство при моделировании более сложных схем. Начальный же расход вполне точно соответствует полученному при аналитическом расчете.
Коэффициент Pipeline pressure loss coefficient принимается для бака равным единице. Также следует внимательнее относиться к установке начальных значений переменным. На рисунке ниже показана настройка блока Бак. В расчетах за начальную переменную принимается исходный уровень, а не объем. Показаны соответствующие настройки приоритета начальных значений, в данном случае, объем 20 л игнорируется (поэтому крестик). При установке равного приоритета обоим начальным значениям переменных, результаты моделирования данной схемы будут неточными.
Установка начальных значений для переменных блока Tank. Красным крестиком отмечена начальная переменная без приоритета. Объём в начале симуляции не равен 20 литрам, он составляет 125 литров и определяется параметрами бака и начальной переменной с более высоким приоритетом. Она отмечена зеленой галочкой.
Аналитическое уравнение
Решение аналитического уравнения.
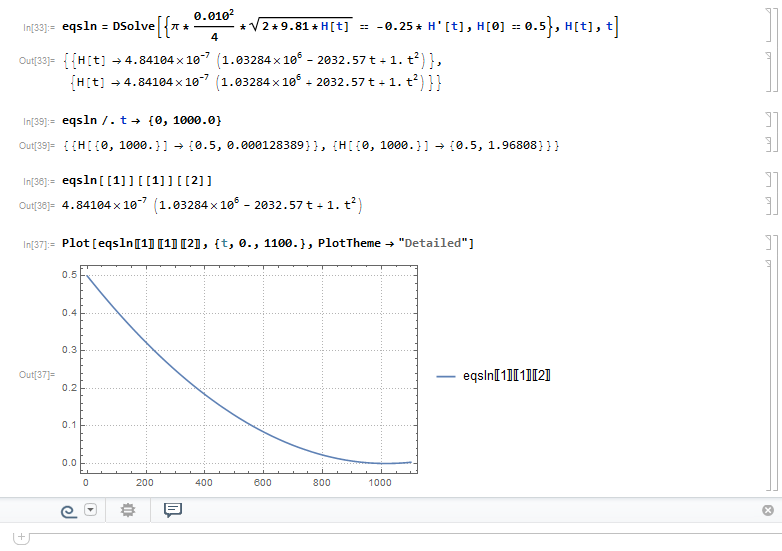Решение ОДУ для определения зависимости уровня от времени по аналитическим выражениям. Кликните для увеличения.
Как видно из рисунка, дифференциальное уравнение представляет собой равенство, в левой части которого расход, полученный при помощи уравнения Торричелли, а в правой части — расход по своему определению. По идее, расход это , но так как стенки бака прямые, площадь мы выносим за производную. Таким образом, уравнение имеет вид:
Его решение показано синей линией на графике уровня от времени. График уровня проходит минимум при .
Источник
Рассмотрим сосуд (рис. 1), площадь горизонтального сечения, которого является произвольной функцией расстояния сечения от дна сосуда.
Пусть высота уровня жидкости в сосуде в начальный момент времени t=0 равна h метров. Пусть, далее, площадь сечения на высоте х равна S(x), а площадь отверстия на дне сосуда есть S.
Известно, что скорость истечения жидкости U в тот момент, когда высота ее уровня равна x, определяется равенством U=k, где g=9,8 м/с2, k – коэффициент скорости истечения жидкости из отверстия. На бесконечно малом промежутке времени dt истечение жидкости можно считать равномерным, а потому за время dt вытечет столбик жидкости, высота которого Udt и площадь сечения S, что в свою очередь вызовет понижение уровня жидкости в сосуде на – dх.
В результате этих рассуждений приходим к дифференциальному уравнению
ksdt = – S(x) dx; (5)
которое можно переписать в виде
dt=-dx; (6)
Решим теперь следующую задачу. Цилиндрический резервуар с вертикальной осью высотой 6 м и диаметром 4 м имеет на дне круглое отверстие радиусом 1/12 м. Требуется установить зависимость уровня воды в резервуаре от времени t, а также определить время, в течение которого вытечет вся вода.
По условиям задачи S(x)=4р; S=1/144. Так как для воды k=0,6, то уравнение (6) примет вид dt = -dx;
Интегрируя это дифференциальное уравнение, приходим к соотношению t= 434,304 ;которое и дает искомую зависимость уровня воды от времени t. Если теперь в последнем равенстве положить х=6, то получим, что вся вода вытечет из резервуара приблизительно через 18 минут.
Вторая задача состоит в следующем. Известно, что древние водяные часы представляли собой чашу (рис. 2), из которой через небольшое отверстие на дне вытекала вода. Такие часы использовались в греческих и римских судах для хронометрирования речей адвокатов, чтобы не допускать слишком долгих выступлений. Требуется найти форму водяных часов, при которой уровень воды убывал бы в чаше с постоянной скоростью.
Задача легко решается с помощью выведенного выше уравнения (6), которое мы только перепишем в виде
=-; (7)
Именно, учитывая, что чашу можно рассматривать как поверхность вращения, в соответствии с обозначениями на (рис. 2) из уравнения (7) получаем, что
(8)
Где a=Ux=- проекция свободной поверхности жидкости на ось x, которая по условию задачи есть величина постоянная. Возведя обе части уравнения (8) в квадрат приходим к уравнению
x=cr4; (9)
где c=a2р2/(2gk2s2). Последнее означает, что форма поверхности водяных часов получается вращением кривой (9) вокруг оси х.
Приведем один из примеров использования дифференциальных уравнений для выбора правильной стратегии при решении задач поиска.
Пусть, например, миноносец охотится за подводной лодкой в густом тумане. В какой-то момент времени туман поднимается и подводная лодка оказывается обнаруженной на поверхности воды на расстоянии 3 миль от миноносца. Скорость миноносца вдвое больше скорости подводной лодки. Требуется определить траекторию (кривую погони), по которой должен следовать миноносец, чтобы он прошел точно над подводной лодкой, если последняя сразу же погрузилась после ее обнаружения и ушла на полной скорости прямым курсом в неизвестном направлении.
Для решения сформулированной задачи введем полярные координаты r, O таким образом, чтобы полюс О находился в точке обнаружения подводной лодки, а полярная ось r проходила через точку, в которой в момент обнаружения подводной лодки был миноносец (рис. 3). Дальнейшие рассуждения основаны на следующих соображениях. Прежде всего, миноносцу надо занять такую позицию, чтобы он и подводная лодка находились на одном расстоянии от полюса О. Затем миноносец должен двигаться вокруг полюса О по такой траектории, чтобы оба движущихся объекта все время находились на одинаковом расстоянии от точки О. Только в этом случае миноносец, обходя вокруг полюса О, пройдет над подводной лодкой. Из вышесказанного следует, что сначала миноносец должен идти прямым курсом к точке О до тех пор, пока он не окажется на том же расстоянии х от полюса О, что и подводная лодка.
Очевидно, что расстояние х можно найти либо из уравнения
,
либо из уравнения
,
где u – скорость подводной лодки, а 2u – скорость миноносца. Решая последние уравнения, находим, что либо расстояние х равно одной, либо трем милям.
Теперь, если «встречи» не произошло, то миноносец должен в дальнейшем двигаться вокруг полюса О (по направлению движения часовой стрелки или против), удаляясь от последнего со скоростью подводной лодки u. Разложим скорость миноносца 2u на две составляющие: радиальную urи тангенциальную ut (рис. 3).
Радиальная составляющая – это скорость, с которой миноносец удаляется от полюса О, т.е.
ur=.
Тангенциальная составляющая – это линейная скорость вращения миноносца относительно полюса. Она, как известно, равна произведению угловой скорости на радиус r, т.е.
ur=r.
Но так как ur = u, то
ur==u.
Итак решение исходной задачи сводится к решению системы двух дифференциальных уравнений
, r= u,
Которая, в свою очередь, может быть сведена к одному уравнению
исключением переменной t.
Решая последнее дифференциальное уравнение, получаем, что
r=C,
где С – произвольная постоянная.
Учитывая теперь, что миноносец начинает движение вокруг полюса О с полярной оси r на расстоянии х миль от точки О, т.е. учитывая, что r=1 при O=0 и r=3 при O=-р я, приходим к выводу, что в первом случае C=1, а во втором С = З. Таким образом, чтобы выполнить свою задачу, миноносец должен пройти две или шесть миль прямым курсом по направлению к месту обнаружения подводной лодки, а затем двигаться либо по спирали r= либо по спирали r=3.
Источник
- gidroadmin
- 3338
Программа предназначена для расчета расхода слива рабочей жидкости из цилиндрической емкости
(опорожнение
емкости) через отверстие или насадок на дне емкости. Позволяет выбрать 15 жидкостей и четыре вида
насадков.
Программа расчитывает изменение основных характеристик – высота Н, расход Q, объем
жидкости в емкости со временем. Шаг расчета можно задать от 1 секунды до 10 секунд.
Также программа расчитывает среднее время по среднему уровню жидкости в емкости. В этом случае время
опорожнения резервуара на 10-20% меньше, чем вычисленное итерационным методом.
Допущения, принятые в расчете
Строго говоря истечение жидкости из емкости или резервуаров при переменном напоре – это
нестационарный процесс, поскольку происходит
постоянное
изменение напора и, соотвественно, скорости и расхода. Однако, в случае, когда уровень
жидкости в
резервуаре
понижается медлено можно принебречь инерционным напором.
Поэтому, для технических целей с допустимой погрешностью
используют формулы для стационарного течения т.е. установившегося течения.Предполагается, что со временем и изменением расхода гидросопротивление насадка не меняется.
Отверстие существенно мало по сравнению с диаметром емкости.
Избыточое давление в газовой подушке емкости в процессе слива принято постоянным. Если это
открытий
резервуар, то избыточное давление равно нулю.
Ввод исходных данных
Введите исходные данные в истеме СИ:
давлений для перевода
одних единиц давления в другие.
вес
технических жидкостей при соотвествующей
температуре
| Время, с | Уровень, м | Объем, м3 | Расход, м3/c | Расход, л/мин |
Вильнер Я.М. Справочное пособие по гидравлике, гидромашинам и гидроприводам.
Что то не то с порядком цифр, считаю бак емкостью 3,5м3, а в расчете выдает 3532500.0000м3
Спасибо за комментарий! Но у меня в тестовых задачах в Excel все сходиться с программой! Вы же имейте ввиду, что средний расход высчитывается по среднему уровню жидкости в емкости при постоянном давлении в подушке емкости. И этот средний уровень как раз равен половине высоте емкости, которую Вы вводите в поле. В любом случае, если есть сомнения, напишите в комментариях свои данные и мы проверим их еще раз в Excel и в программе.
Считает не правильно.
Что-то с высотой жидкости в емкости. Если подставить значение в 2 раза больше, тогда все сходится.
Спасибо за комментарий! 1. Вязкость никак не участвует в формуле истечения, разве что опосредовано через число Рейнольдса, но при истечении Рейнольдс достаточно большой, и этим влиянием принебрегают и фактически коэффициент расхода остается постоянным в процессе истечения. 2. Да нет, ничего не перепутано, хотя на первый взгляд может показаться, что из-за сопротивления насадка расход через него должен быть меньше, чем через простое отверстие. Но из-за того, что в цилиндрическом насадке на расстоянии равном где-то радиус отверстия возникает вакуум, расход жидкости увеличивается из-за дополнительного подсоса жидкости в насадке. Минимальный коэффициент расхода имеет конический расходящийся насадок, затем отверстие. Значение коэфициента расхода отверстия приведено здесь. Там же хорошее видео по теме истечения жидкости из резервуаров и типы насадков. Также значения коэффициентов расхода различных насадков приведены в таблице.
Если уж вводите тип жидкости, т.е. берете табличные значения вязкости, то уж плотность жидкости можно было бы вставить так же из табличных значений.
1. Перепутаны “Коэффициенты расхода”, у простого отверстия минимальное гидравлическое сопротивление.
2. Диаметр насадки, а не “насадка”.
Источник