Все о вакууме в сосуде

Очень часто к нам обращаются люди, которые хотят купить вакуумный насос, но слабо представляют, что такое вакуум. Попытаемся разобраться, что же это такое. По определению, вакуум – это пространство, свободное от вещества (от латинского слова «vacuus» – пустой). Существует несколько определений вакуума: технический вакуум, физический вакуум, космический вакуум и т.д. Мы будем рассматривать технический вакуум, который определяется как сильно разреженный газ. Рассмотрим на примере, что такое вакуум и как его измеряют. На нашей планете существует атмосферное давление, принятое за единицу (одна атмосфера). Оно меняется в зависимости от погоды, высоты на уровнем моря, но мы не будем принимать это во внимание, так как это не будет никак влиять на понимание понятия вакуум. Итак, мы имеем давление на поверхности земли равное 1 атмосфере. Всё, что ниже 1 атмосферы (в закрытом сосуде), называется техническим вакуумом. Возьмём некий сосуд и закроем его герметичной крышкой. Давление в сосуде будет равно 1 атмосфере. Если мы начнём откачивать из сосуда воздух, то в нём возникнет разряжение, которое и называется вакуумом. Рассмотрим на примере: в левом сосуде 10 кружочков. Пусть это будет 1 атмосфера. «откачаем» половину – получим 0,5 атм, оставим один – получим 0,1 атм.
Так как в сосуде всего одна атмосфера, то и максимально возможный вакуум мы можем получить (теоретически) ноль атмосфер. “Теоретически” – т.к. выловить все молекулы воздуха из сосуда практически невозможно. По этому, в любом сосуде, из которого откачали воздух (газ) всегда остается какое-то его минимальное количество. Это и называют “остаточным давлением”, то есть давление, которое осталось в сосуде после откачки из него газов. Существуют специальные насосы, которые могут достичь глубокого вакуума до 0,00001 Па, но всё равно не до нуля. В обычной жизни редко когда требуется вакуум глубже 0,5 – 10 Па (0,00005-0,0001 атм). Есть несколько вариантов измерения вакуума, которые зависят от выбора точки отсчёта: 1. За единицу принимается атмосферное давление. Всё, что ниже единицы – вакуум. То есть шкала вакуумметра от 1 до 0 атм (1…0,9…0,8…0,7…..0,2…0,1….0). 2. За ноль принимается атмосферное давление. То есть вакуум – все отрицательные числа меньше 0 и до -1. То есть шкала вакуумметра от 0 до -1 (0, -0,1…-0,2….,-0,9,…-1). Также шкалы могут быть в кПа, mBar, но это всё аналогично шкалам в атмосферах. На картинке показаны вакуумметры с различными шкалами, которые показывают одинаковый вакуум:
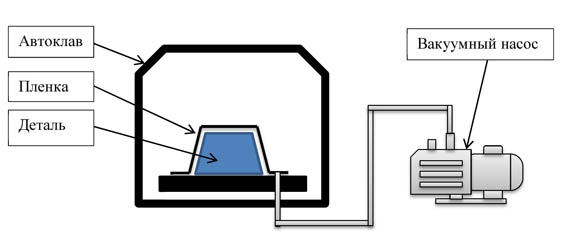
Из всего сказанного выше видно, что величина вакуума не может быть больше атмосферного давления. К нам почти каждый день обращаются люди, которые хотят получить вакуум -2, -3 атм и т.д. И они очень удивляются когда узнают, что это невозможно (кстати, каждый второй из них говорит, что “вы сами ничего не знаете”, “а у соседа так” и т.д. и.т.п.) На самом деле, все эти люди хотят формовать детали под вакуумом, но чтобы прижим детали был более 1 кг/см2 (1 атмосферы). Этого можно достичь, если накрыть изделие плёнкой, откачать из под неё воздух (в этом случае, в зависимости от созданного вакуума, максимальный прижим составит 1 кг/см2 (1 атм=1 кг/см2)), и после этого поместить это всё в автоклав, в котором будет создано избыточное давление. То есть для создания прижима в 2 кг/см2, достаточно создать в автоклаве избыточное давление в 1 атм.
Теперь несколько слов о том, как многие клиенты измеряют вакуум на выставке ООО “Насосы Ампика”, у нас в офисе: включают насос, прикладывают палец (ладонь) к всасывающему отверстию вакуумного насоса и сразу делают вывод о величине вакуума. Обычно, все очень любят сравнивать советский вакуумный насос 2НВР-5ДМ и предлагаемый нами его аналог VE-2100. После такой проверки, всегда говорят одно и тоже – вакуум у 2НВР-5ДМ выше (хотя на самом деле оба насоса выдают одинаковые параметры по вакууму). В чем же причина такой реакции? А как всегда – в отсутствии знаний законов физики и что такое давление вообще. Немного ликбеза: давление «P» – это сила, которая действует на некоторую площадь поверхности, направленная перпендикулярно этой поверхности (отношение силы «F» к площади поверхности «S»), то есть P=F/S. По-простому – это сила, распределённая по площади поверхности. Из этой формулы видно, что чем больше площадь поверхности, тем меньше будет давление. А также сила, которая потребуется для отрыва руки или пальца от входного отверстия насоса, прямо пропорциональна величине площади поверхности (F=P*S). Диаметр всасывающего отверстия у вакуумного насоса 2НВР-5ДМ – 25 мм (площадь поверхности 78,5 мм2). Диаметр всасывающего отверстия у вакуумного насоса VE-2100 – 6 мм (площадь поверхности 18,8 мм2). То есть для отрыва руки от отверстия диаметром 25 мм, требуется сила в 4,2 раза большая, чем для диаметра отверстия 6 мм (при одинаковом давлении). Именно по этому, когда вакуум измеряют пальцами, получается такой парадокс. Давление «P», в этом случае, рассчитывается как разница между атмосферным давлением и остаточным давлением в сосуде (то есть вакуумом в насосе). Как посчитать силу прижима какой-либо детали к поверхности? Очень просто. Можно воспользоваться формулой приведенной выше, но попробуем объяснить попроще. Например, пусть требуется узнать, с какой силой может быть прижата деталь размером 10х10 см при создании под ней вакуума насосом ВВН 1-0,75. Берём остаточное давление, которое создаёт этот вакуумный насос серии ВВН. Конкретно у этого водокольцевого насоса ВВН 1-0,75 оно составляет 0,4 атм. 1 атмосфера равна 1 кг/см2. Площадь поверхности детали – 100 см2 (10см х10 см). То есть, если создать максимальный вакуум (то есть давление на деталь будет 1 атм), то деталь прижмётся с силой 100 кг. Так как у нас вакуум 0,4 атм, то прижим составит 0,4х100=40 кг. Но это в теории, при идеальных условиях, если не будет подсоса воздуха и т.п. Реально нужно это учитывать и прижим будет на 20…40% меньше в зависимости от типа поверхности, скорости откачки, и т.п. Теперь пару слов о механических вакуумметрах. Эти устройства показывают остаточное давление в пределах 0,05…1 атм. То есть он не покажет более глубокого вакуума (будет всегда показывать «0»). Например, в любом пластинчато-роторном вакуумном насосе, по достижении его максимального вакуума, механический вакуумметр всегда будет показывать «0». Если требуется визуальное отображение значений остаточного давления, то нужно ставить электронный вакуумметр, например VG-64. Часто к нам приходят клиенты, которые формуют детали под вакуумом (например, детали из композиционных материалов: углепластика, стеклопластика и т.п.), это нужно для того, чтобы во время формовки из связующего вещества (смолы) выходил газ и тем самым улучшались свойства готового продукта, а так же деталь прижималась к форме плёнкой, из-под которой откачивают воздух. Встаёт вопрос: каким вакуумным насосом пользоваться – одноступенчатым или двухступенчатым? Обычно думают, что раз вакуум у двухступенчатого выше, то и детали получаться лучше. Вакуум у одноступенчатого насоса 20 Па, у двухступенчатого 2 Па. Кажется, что раз разница в давлении в 10 раз, то и прижиматься деталь будет гораздо сильнее. Но так ли это на самом деле? 1 атм = 100000 Па = 1 кг/см2. Значит разница в прижиме плёнки при вакууме 20 Па и 2 Па составит 0,00018 кг/см2 (кому не лень – посчитает сам). То есть, практически, разницы никакой не будет, т.к. выигрыш в 0,18 г в силе прижима погоды не сделает. Расчет времени вакуумирования емкости Как рассчитать за какое время вакуумный насос откачает вакуумную камеру? В отличии от жидкостей, газы занимают весь имеющийся объем и если вакуумный насос откачал половину воздуха, находящегося в вакуумной камере, то оставшаяся часть воздуха вновь расширится и займет весь объем. Ниже приведена формула для вычисления этого параметра. t = (V/S)*ln(p1/p2)*F, где t – время (в часах) необходимое для откачки вакуумного объема от давления p1 до давления p2 V – объем откачиваемой емкости, м3 S – быстрота действия вакуумного насоса, м3/час p1 – начальное давление в откачиваемой емкости, мбар p2 – конечное давление в откачиваемой емкости, мбар ln – натуральный логарифм F – поправочный коэффициент, зависит от конечного давления в емкости p2: – p2 от 1000 до 250 мбар F=1 – p2 от 250 до 100 мбар F=1,5 – p2 от 100 до 50 мбар F=1,75 – p2 от 50 до 20 мбар F=2 – p2 от 20 до 5 мбар F=2,5 – p2 от 5 до 1 мбар F=3 В двух словах, это всё. Надеемся, что кому-нибудь эта информация поможет сделать правильный выбор вакуумного оборудования и блеснуть знаниями за кружкой пива… |
Источник
Pages: | | 2 | 3 | 4 | 5 | — [ 1 ] — 1. , , : , . ( . vacuum ) . , . . . , . , , , : . , , , . . . , [1] . . , ( ) . , . , . , ( , ) . , , . . , , . , , , ( 1 , 1=133.3223684 =0,001315789474 =1 ..) . , , . , . d, d , , , (10-5 ). 10-9 . , , 10 . , . , , . . , , . . , ( ). , , , . : ; , ; ; , 4,2 .. , : -, . : ; ; ; ; . (. .1): ; ; -. .1. – 2 3. 1*10-1 1*10-2 …, 2 ; 3, . , . ; , . ( ), 3 1. (.2). , , . . (.3) (, ) 1, 3 . . 2. 1*10-2-1*10-1 … ( ) . .2* (.2*). (1) (2). , . . (3) – . : (I) (II). , (4). , , . . , , 106 3 , , – . . , 0,1% . 1892 . . , . . .4 (.301. ) , , . , , . ( ) . .4. : 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 – ; 9 ; 10 . , . ; , , (. . 2.11). ( ). , – . , . . , . : 1) . – , . 2) – , , . 10%. , 106 3 116,6 3. . , . , , . , , . , , , . , : Q=Q+Q, Q ; Q – ( ). Q : Q=5,7((T1/100)4-(T2/100)4)E F2, , (*) T1 T2 () () , ; F2 , 2; E , ( , , , E=1); , =1/(1/e2+F2(1/e1-1)/F1). , , . 1 , 2 , (- , , , ) 1.11. (.187 ) 300 78 4, 0,03 – – 0,03 0,019 0, 0,03 0,018 0, . 0,10 0.06 0,6 – 0,94 – 1) F1 F2. : , .. 2) , , , , . 3) , , . . . ( ..), , . F1 =F2 e1= e2= Ne=Ee/(N+1), N , Ee Ee=/(2-e). .., 2 , .. . (, ), (*). ( : =(14-24), 1 , 2 ) , , , , (.5., . 227, .118). 1, . 3 . , , . . ( , ). (*), , (14-He4)/ (N2 4-He4)=(3004-4,24)/(784-4,24)220 1% . 2-4 . – . , . – 25 (.6., .227 119 ). 2 3. , 4; . . 2,8% . , , – , -. , 340 3 10,7 ( . ). , ( ) 750 , 0,13% . . 5. , . 6. : – 1- 2 ; 2- N2; , 3- ; : 4-; 5 1 ; 2-; 3-; 4- ; 5-; 6- ; 7- : -Bio ” “, 10 . . . () . , . . ( .) , . . , . 2- ( , ). . : ( ), , . ( , ). , , , 10001200 . 11 . . , . , , , . , . , 50 , . . , . 80 , , 110 C (160 ). . 720 . , , ( ), 3000 C. . , , , , . – , , , , , . . , . . ( . %) : 78,08%, 20,95%, 0,93%, ( ) 0,034%, 5105 %; , ( , ) : 1,8103 %, 5,24104 %, 1104 % 8106 %. ; . , , , . , . , % , % , 3/ N2 780 870 78,087 75, O2 209 500 20,95 23, Ar 9 300 0,93 1, 300 0,03 0, CO 18*10-4 12,5*10- Ne 5,24*10-4 0,72*10- He 5, 2,03*10-4 1,28*10- 2, 1,5*10-4 0,8*10- CH4 1, 1,14*10-4 3,3*10- Kr 1, 0,5*10-4 0,035*10- H2 0, 0,5*10-4 0,8*10- N2O 0, 0,08*10-4 0,36*10- Xe 0, 0,01*10-4 0,015*10- O3 0, 6*10-14 6*10-18 7*10- Rn 999 999 99,9999 99, , , , . . , , . , , () , – . 1883 . .. . -, , , , , , -, . , , , . – , . . . (, , ) . – , . . . . . – , . . , () . , . , . . , (). . . , , . . , , . , . , , , . ( ) . , , , . . , , , ( ), ( ). , ( ) . , . , .. , . , , , , , . , , , , . . , . , . . . , , . , ( ). . . . – . : , . , , ( ) . . . 20 , 105 14 . . . . . D2O, . – : 1/6400, . . . ( ), . 3 , . : ( ) , . , , . .., , , , , , . 1.6 ( , , *) 2, N2 . , . , , – . . . – ( ). . : , , , , , . , , , , . . – . . , . . , . , , . , ( . , ), , , . , (). (), , , , , ., . . . N2 , – = SiO2/Al2O3 2, . (, , , , , .; . . : , , , , , , , , ; . . ). – . , , 20-30 0,1-0,6 , – 20-30 . -, 2 (30-95%). , , . , 80% 2, , . 0,3-0,8; 0,2 1,0 */3 . 2 (., , ). 2 , 2 (2,8-10-10 ). N2 . , N2 2 2%, 2 – 40%; 5 -. 4 77%. , , , 0,1-0,6 , 0,5 3,0% 2. , . , 50-60% 2, – 90-95%. 30 3/ 1 . Ne – . , 50% , N2 – 190 200 , . , Ne . , He-Ne , , Ne, 0,1-0,2% . Ne 0,6-0,8. Kr-, , 0,1-0,2% – . , (., 123) 650-750 . 2, r- 500 1000 . , – . Kr- (. ). . . . , , . ; , , . . . – . , , , – ; – , . : () () . , , , – . 2 , () . 2 ; , N2, . 2 N , . , . , , 2: , . , (. . . . ), , . 90-97%- N2 , , , , . , , . : 1) , , , 2) () 3) ( 150) . . () ; . , ., : L =, – , – . , , ( ), . . , 1 99,5%- 2 0,38-0,42 *, LMH = 0,067 *. (, , .), 2 . . . , , , . . , , , . – , , . , , . ( ). ( ) ( ). . , , , . , , . , . . , . , , 100 . 0,6 . , . . , , , 40 (230 ) . , , , . , , , ( ). , , , . , . , , ( ). . (-). , , , , . , , , . , . . , , , , , . . , . , , , . . , , , . 80 (190 C); . 79% 21% , 65% 35% , 87% 13% . , . , . , , . , , ; , , , . , , , , . , . – . , , , . , , . . (, , ) , – . , . . , , . . 17 . 12 ; . 2, , , , , , – , . P, 105 , P, 10 , 647 218 ( 2) 132 38, 405 112,3 126 33, 304 72,7 33 13, 154 49,7 5 2, , . , . . . (), . . , , , , .. 20 (293 ), 0 (-273 ) . , 120 (-153 ), , , , . ( 13- 1971 , 120 ). . – . – , , . , , , , , , , . , , , . . , – , , ( ). , , , , () . – , , (182,97 , 90,19 ). (3 K), . . , , . . , NH4NO3 , 257 . 1759 . .. .. ( 210 ) ( ). ( 200 ) , ( ) . , 196 , , 196 . ., 36 2, ( ), , . -790 , , -1000 . : , , ( ) . , , , () . . , . . . () (). , . , ( ) (. 1.1). () 1792 ( . ). 1823 (. ), 1877 ( . . . ), 1883 (. . . ), 1898 (. ), 1908 (. -). .1. , . . ., . . : 77 63 , 27 24 , 20 14 , 4,2 1 . . . , , . , , , . ( ) . . . . , , , ( , , ), . 1. . . ( ), () ( ), () 182,97 (90,19) 218,75 (54,41) 195,81 (77,35) 210,05 (63,11) 246,09 (27,07) 248,58 (24,58) 252,78 (20,38) 259,19 (13,97) -4 268,93 (4,23) -3 269,93 (3,23) -189,36 (83.8) . ( . .72 ). 1823 .. , , , , ( 110 ). , , , , , , . 1877 . () . () , . , , , . , . 1887 . . . , , , , . 1894 .- () . , . , -, . 1895 . () . () , . . . , . 1898 . , . , 19 . , , . 4 (-4) – 1908 , . , . , 1930 ., , 1934 .. (). 1946 . (). 3, , 1948 – (). , 0,25 . .2. 2. 1780 ., . 1787 .- 1788 . 1823 , , . , 1834 . 1845 , . , , , , , 1845 , . , , , , , . 1861 .. 1862 . 1869 – ., . 1877 : ., . ., . 1883 : 1885 1895 1897 . 1897 . 1895 . 1884 1898 . 1898 . 1902 . 1908 .- . , . , X, s=f(T,X). (1.1) , (1.1), . (1.1) , . . X p, X H, E. , (1.1) . s=const. (1.1) s T (.3.1). , X1. X X1 X4 ( -) s s. , p1 p4, . Q=T*(s-s). (2.1) , ( ), X X1 ( -). s=s, : , X, c , T. , . .. (. Detendre- ) p4 p1. , , X. .3. S-T / , (). , , S T, T S. 2 2 S=S2-S1= dQ / T = dU / T + pdV / T = ..p=const,V=TR/p,dV=(R/p)dT= 1 1 T2 cv dT/T+p ( R / pT )dT =cvln(T2/T1)+Rln(T2/T1)=(cv+R)ln(T2/T1)=cpln(T2/T1). T1 T S2S, T2T. S= S1 + ( dU + pdV ) / T = cpln(T/T1)+ S1. T T=T1e(S-S1)/cp. , S1 , .. , . , . s=f(T,X): X, . , X T, . , , . , 1906 . : , .. T00 s0. . : =00 s0=0. , , . : , . , , , , , . . , T00 . , 0. , , , . T00 T X, . .4.1 – , =0. . .4. . : ( ); (, ) ( ); ( -) ( ); , . , , . – , . : PV= const, P , V , , cp cv, . (r, Ne .) =1,67, (H2, O2, N2 .) =1,4. PV = RT, TV-1= const. 1, , , . , , . , – . , , , , . , . . , . , , . . , ( ). . 1. ( ). . , – PV=RT (1.2) ( , .. ) P1V1 k= P2V2 k= PVk=const (2.2), k , k= Cp/Cv. (1.2) P=RT/V (2.2): T1V1 k-1=T2V2 k-1, .. T2/T1 =(V1/ V2)k- , V=RT/P, : T2/T1 =(P2/ P1) (k-1)/k (3.2) .. k. =Cp/Cv =Cp /(Cp-R), Cp-R=Cv, (k-1)/k=R/ Cp Cp P T, Cp 1,3-1,7 T2/T1 =(P2/ P1)R/Cp (4.2) , Cp-R=Cv, .. Cp =Cv +R, .. . , R. T Q. C=Q/T. , , U . Q=U+ (V=0) 0, Q=U. C=Cv=U/T. =PV, Q=U+=U+ PV, T ( ) Q/T= U/T+ PV /T, C=Cp= Cv+ PV /T (*). , Cp Cv , 10. , Cp Cv , PV=RT, PV RT (*), Cp =Cv +R : T2 =T1(P2/ P1)R/Cp, (5.2) 1 T2 T1. , , . , . , 80 200 1 , k=1,4 84 . , , (. Detendre- ) , . . , .. , ( ..). , , . , . ( ) … , i-i=h h, i i- . i=U+pv. …=h/ h (6.2) 2. (, ) ( ) , , . , , . , . , . , , , . L=vv dv= (v-v). (7.2) (Q=0), , : U-U= (v-v). i=U+pv, i= i-i= v(1-/)- . (8.2) v=RT i=cpT, : T=T-T= T*((k-1)/k))*(1- /). (9.2) T . – ., 36 2, ( ), , . -790 , , -1000 . ( 1. s200.pdf) 3. . , . ( ). ( . drosseln , ) : , . – , , . , . (. 5) , , ( ). 1 2 . . 5. – , V1, V2 . (Q=0), , : = 1V1- 2V2 (10.2) : U = U2 U1 = 1V1- 2V2 (11.2) U1 + 1V1 = U2 + 2V2 (12.2) 1 = 2 (13.2) = U + V . , – . , – PV=RT (14.2), : dU=McvdT (15.2) dH=McpdT (16.2) . , – , . , — : (p + a/V2)(V b)=RT (17.2) , – , . 1. , (b0), (=0). : p(V b)=RT (18.2) pV =RT + p b (19.2) : U = 1V1- 2V2 = R(T1 2) + b(1 2) (20.2) , : U b(1 2) (21.2) 1 2 (21.2) , . , , , – (0 ) 2. (0), (b=0). : (p + a/V2)V=RT (22.2) pV =RT – /V (23.2) : U = 1V1- 2V2 = R(T1 2) + (1/V2 – 1/V1) (24.2) , , : U (1/V2 – 1/V1) (25.2) V2 V1- (25.2) , , . , , , – (0 ). , , – , 1 (2/Rb). – (0) 12/Rb. 12/Rb, (0). ()max =2/Rb (26.2) () ( ). : He 40 K 2 202 Ne 231 K N2 621 K O2 764 K 2 1900 , 2, O2 N2 . He, 2 Ne . , 2.2. 6. . Pages: | | 2 | 3 | 4 | 5 | |
Источник
, , , , .
– , . , . , . , . , .
, , , , , , . : , ? , , , . , . , , , , , . – ?
, , – . . , : , . – , – , – . , , , .
– [1]. , . , – .
” , , . , , . . , , , , , , . , , , . , , , , .. “[2] .
– . – . , , , . . – – .
. – – .. . , , ” ” ()[3], . , . . :
1. . , . “”, ( 10–30 ).
2. , “”. – (10 ) , ( ). .
3. . , , , , .
4. . , , (” ” ” “).
5. “”. . “” “” – . , “” . , “”, ” “. , .
6. , ” “. ( 5 20 ” “). (1982 .) . , . . , “” , “”.
7. . .
8. . ” ” – .
9. “” (sprites), (elves), (jets)”. . “” – ( ~100 ) 30 20-100 . – “” ” ~40 “. “” – “” 100 , . “SPACE SHUTTLE” .
10. . , , , , , . .
C : , , , , , . , , , . , – , 4.
, .. , . – , [5].
– – , .
, , .
, , , .
.. , . , , . -, . , , , , . , , .
: ? . , , , .
: (), (), , , (), , .
, (), . . 6. , . – . , . .
, . , . , . , , , .
, , , (.-, 1911 .) (.., 1938 .), . , , . , , . . , . , . , , , . , 100 (1893 .), …
, , . , , . , . , , , ..7. , , , , . , ? , , . , .
, , . , , . , , , , . , , , . , . , , : . , , . , , .
, , , , , . , , , , , , [8].
, , . .
– , . . , . – : , , .. , , , , .
, – , , , , . , . , , . .
, . . .
, , , , . , , . , . . , , , [9].
, 3000 1000- 1,45 , 20 , 1000- 9,64 .
, , . , . . . , . , , , . .
. 80- XX .. . .
, , , . .
70- : ? , , . , . . , , 10.
– . .. , , , .
, – , , , , , , . , , .
, , , , . . , .
, , , , , 1869 , , , 1, , , , , … , , I , , , , I , , . 1- 0 . y . , , . , , [11].
, .. y, 0,4 .
, , . . , , , , , , , . . 1869 , , , , , – , 531,7 ( ??, . . , 5317, 1474), : 587 ??. , , (1898) , , , . , , , , [12].
. . , 0,2 , ; ( ) [13]. , 2,2414 , , . , , 11 . , – .
, , , , . , , , , 1-, . . , . , , , , , -, , , , -, , -, – – , , -, – , , . , , , , – [15].
, .. , – 0,000013 , 1,451 10-33 . . , , 90 , 10-16 . , , .
, . . . . , , . , .
, , , . , . . , , , : , , , , , , .
, . . . . , . , . .
, , . , , , . . , 353 /, 1300 /
, , , , ; .
, , . , – 1,82 10-30 . 0,000013 , 1,451 10-33 . , . . , , .
, , , . , , . . . , .
, – . . – , , , .
? , [16].
, . ? , , – . , , . , , . .
, : , , , , , , , , , . , , , , . . , . . . , , . , , . , .
.
, . . ? . . ! . , . , , , , , , , .
, . 17, . , , , . , . , . , – . . , , , , , , .
, .. , , [18].
, , , , , 19, , , , , , .
2004 .
[1] – , – . . ., , , : , , .. ()
[2] . . – .: , 1957 .
[3] .. . – : . – , 1998. – 191 .
[4] .., .. . :, 1995. ( / ; 16). 34 . // . 1996. . 3.-. 65-76.
[5] .. . – : – – , 1998. 184 . ( ).
[6] .. . – .: , 1990. – 280 .
[7] .. . : . – , 1998. -191 .
[8] N.Tesla, Pioneer Radio Engineer Gives Views on Power New York Herald Tribune, Sept.11, 1932.
[9] .., .. ., , 1972 . – 816 .
[10] . . . 2 ., .-, 1910 .
[11] .
[12] . . . 2 ., .-, 1910 .
[13]
[14] 1843 2,24 = 4128,32 / (.).
[15] . . . 2 ., .-, 1910 .
[16] ., ., ., .: , 1981 .
[17] .
[18] , .
[19] , , (. . . . 2 ., .-, 1910 .)
Источник