Вычисление давления на дно сосуда
Разработки уроков (конспекты уроков)
Линия УМК А.В. Перышкина. Физика (7-9)
Физика
Внимание! Администрация сайта rosuchebnik.ru не несет ответственности за содержание методических разработок, а также за соответствие разработки ФГОС.
Тип урока: Урок открытия и первичного закрепления знаний.
Цель урока: получить выражение для расчёта давления жидкости на дно и стенки сосуда; проверка качества знаний учащихся при решении задач.
Задачи урока:
- Предметные: углубить и закрепить знания о давлении жидкости.
- Метапредметные: продолжить развивать внимание, память, логическое мышление, умение делать выводы.
- Личностные: способствовать формированию научного мировоззрения, активизировать учебно-познавательную деятельность учащихся, содействовать формированию самостоятельности, воспитанию интереса к предмету.
Оборудование к уроку: компьютер, видеопроектор, интерактивная доска, два стакана с водой, цилиндрические сосуды с основаниями различной площади, деревянный брусок, камень, два одинаковые пластмассовые груза, широкий сосуд, аквариум, удочка, каточки с заданиями, учебник по физике.
Ход урока
1.Организационный момент.
2. Актуализация имеющихся знаний.
Взаимопроверка в парах по вопросам. Слайд 1
- Чем отличается процесс передачи давления в жидкости и газе от передачи давления твёрдыми телами? (давление твёрдыми телами передаётся в направлении действия силы, в жидкости и газе по всем направлениям одинаково)
- Сформулируйте закон Паскаля. (давление, производимое на жидкость или газ, передаётся в любую точку без изменений во всех направлениях)
- Мальчик выдувает мыльные пузыри. Почему они принимают форму шара? (они приобретают форму шара, так как давление в газе, согласно закону Паскаля передаётся одинаково по всем направлениям)
- От чего зависит давление газа? (от объёма, массы и температуры газа)
- Для космонавтов пищу изготавливают в полужидком виде и помещают в тюбики с эластичными стенками. Что помогает космонавтам выдавливать пищу из тюбиков? (Закон Паскаля)
- Почему взрыв снаряда под водой губителен для живущих в воде организмов? (давление взрыва в жидкости, согласно закону Паскаля, передаётся одинаково по всем направлениям, и от этого животные могут погибнуть)
- Почему пловец, нырнувший на большую глубину, испытывает боль в ушах? (с глубиной давление увеличивается; пловец испытывает боль в ушах, так как вода с большой силой давит на барабанные перепонки)
3. Открытие нового знания. Слайд 2
В три сосуда с одинаковой площадью дна, стоящие на столе, налили воды до одного уровня
1) В каком сосуде масса воды больше? Меньше?
2) Одинаковым ли будет давление воды на дно сосудов?
Вы уверены? Как рассчитать давление жидкости на дно сосуда? (Затруднение).
- Какая цель нашего урока? (Узнать, как рассчитать давление жидкости на дно сосуда)
- Какая тема урока? (Расчёт давления жидкости на дно и стенки сосуда) Слайд 3
Учащиеся записывают тему к себе в тетрадь.
Попытаемся вывести формулу для расчёта этого давления. Но какую же форму сосуда нам надо выбрать для расчёта нашей формулы? Я предлагаю взять форму прямоугольного параллелепипеда.
Для того чтобы упростить вывод формулы для расчета давления на дно и стенки сосуда, удобнее всего использовать сосуд в форме прямоугольного параллелепипеда (Рис. 2).
Рис. 2. Сосуд для расчета давления жидкости
Площадь дна этого сосуда – S, его высота – h. Предположим, что сосуд наполнен
жидкостью на всю высоту h. Чтобы определить давление на дно, нужно силу,
действующую на дно, разделить на площадь дна. В нашем случае сила – это вес жидкости P, находящейся в сосуде
Поскольку жидкость в сосуде неподвижна, ее вес равен силе тяжести, которую можно вычислить, если известна масса жидкости m.
P = mg
Напомним, что символом g обозначено ускорение свободного падения.
Для того чтобы найти массу жидкости, необходимо знать ее плотность ρ и объем V
m = ρV
Объем жидкости в сосуде мы получим, умножив площадь дна на высоту сосуда
V = Sh
Эти величины изначально известны. Если их по очереди подставить в приведенные выше формулы, то для вычисления давления получим следующее выражение:
В этом выражении числитель и знаменатель содержат одну и ту же величину S – площадь дна сосуда. Если на нее сократить, получится искомая формула для расчета давления жидкости на дно сосуда:
p = ρgh
Итак, для нахождения давления необходимо умножить плотность жидкости на величину ускорения свободного падения и высоту столба жидкости.
Полученная выше формула называется формулой гидростатического давления. Согласно этой формуле гидростатическое давление не зависит от формы сосуда, в котором находится жидкость и от площади его сечения. Оно зависит от высоты столба жидкости и от плотности жидкости.
Возвратимся к нашему вопросу: Одинаковым ли будет давление воды на дно сосудов? (одинаковым)
Данная формула позволяет найти давление на дно сосуда. А как рассчитать давление на боковые стенки сосуда? Чтобы ответить на этот вопрос, вспомним, что на прошлом уроке мы установили, что давление на одном и том же уровне одинаково во всех направлениях. Это значит, давление в любой точке жидкости на заданной глубине h может быть найдено по той же формуле.
Возвратимся к нашему вопросу: Одинаковым ли будет давление воды на дно сосудов?
4. Физминутка (под медленную, спокойную мелодию)
– Я предлагаю вам, ребята, выполнить дыхательную гимнастику:
1-е упр. Набрать воздух в лёгкие (вдыхаем медленно, но как можно больше воздуха),
Медленно выдохнуть
2-е упр. Руки медленно поднимаем вверх и делаем (одновременно) глубокий вдох.
Руки опускаем – выдох.
3-е упр. Глубоко вдохнуть, садясь за парту, медленно выдыхаем (гимнастика проводится под спокойную музыку).
– Сейчас вы выполнили дыхательную гимнастику, которую врачи рекомендуют проводить 3-4 раза в день.
– А какой физический закон лежит в основе дыхательной гимнастики, как он называется? (в основе дыхательной гимнастики лежит закон Паскаля)
5. Закрепление материала.
Решение задач.
а) Проведение игры «рыбалка»
Качественные задачи:
- Куда бы вы перелили сок из литровой банки, чтобы его давление на дно сосуда стало больше: в пятилитровую кастрюлю или в литровую бутылку? (в литровую бутылку)
- Какие из жидкостей: вода или керосин оказывает меньшее давление на дно сосудов одной формы, если объёмы жидкостей одинаковы? (керосин)
- Как изменится давление воды на дно доверху наполненного стакана, если в воду опустить камень? (не изменится)
- В цилиндрический сосуд, частично наполненный водой, опустили деревянный брусок. Как изменится давление воды на дно сосуда? (увечится)
- Два одинаковых предмета были опущены в цилиндрические сосуды с основаниями различной площади. В цилиндрических сосудах уровень воды до погружения предмета одинаков. В каком сосуде гидростатическое давление больше? (в сосуде меньшей площади)
Ответы на задачи подтверждаются опытами.
б) Расчётные задачи:
- упр. 17(2)
- Определите высоту столба керосина, который оказывает давление на дно сосуда равное 8 кПа. Слайд 4
Самостоятельная работа по решению задачи упр.17(1) по рядам?
6. Подведение итогов урока. Рефлексия.
Подведём итоги.
Давайте вспомним, что сегодня делали на уроке, что узнали?
Мне очень важно, с каким настроением вы уходите с урока. Поэтому я прошу вас заполнить лист самоанализа, который находится столах у каждого из вас.
Лист самоанализа (нужное подчеркнуть)
Чувствую вдохновение, подавленность .
Интересно, неинтересно.
Не устал(ла), устал(ла).
Доволен(довольна), недоволен(недовольна).
Вызвало затруднения(перечислить)…
7. Домашнее задание. Слайд 5
п. 40, упр.17(3), задания на с.118
Источник
Что такое давление жидкости
Наука гидростатика исследует ситуации, когда движение в жидкости отсутствует или скорость пренебрежимо мала, и позволяет понять некоторые свойства такой важной гидродинамической величины, как давление.
Теорема
Давление – физическая величина, описывающая силу, которая действует перпендикулярно поверхности на единицу ее площади. Для ее обозначения используется символ р или Р.
На опору под действием силы тяжести давят и твердые, и сыпучие вещества, но их воздействие отличается от гидростатического давления. Воздействие твердого тела определяется его весом, жидкости – ее глубиной. В газе и жидкости давящее воздействие на поверхности создается за счет хаотических столкновений молекул и связано с другими параметрами состояния вещества – например, температурой Т и плотностью (rho.)
Для жидкости, учитывая ее малую сжимаемость, вместо уравнения Клапейрона, учитывающего температуру и молярную массу газа, обычно используют условие несжимаемости, которое существенно упрощает уравнения гидроаэромеханики:
(rho = const.)
Сила гидростатического давления р на дно сосуда не зависит от его формы и изменяется пропорционально уровню налитой в сосуд жидкости и ее плотности в соответствии с основной гидростатической формулой:
(р = р_{0} + rhos gs h.)
(rho) здесь – плотность вещества, (р_{0}) – атмосферное давление, g – ускорение свободного падения, h – глубина погружения.
История открытия
Гидростатика как наука была достаточно хорошо известна еще в античные времена, поскольку она тесно связана с практической деятельностью людей. Для строительства лодок и кораблей, колодцев и различных гидравлических аппаратов, например, поршневых насосов, необходимо было понимать, как вода взаимодействует с твердыми материальными предметами.
Различие между давлением твердого тела и воды очень эффектно пояснил на опыте Блез Паскаль: всего лишь стакан воды, вылитый в высокую тонкую трубку, соединенную с наполненной водой закрытой бочкой, создал такое избыточное давление, что вода через щели брызнула наружу.
Определение
В 1653 году Паскаль сформулировал свой закон: давление, производимое на жидкость или газ, передается в любую точку одинаково.
Позже был сконструирован прибор, демонстрирующий действие закона Паскаля. Он называется шар Паскаля и представляет собой заполняемый водой шар с маленькими отверстиями, соединенный с цилиндрической рукояткой, внутри которой движется поршень. Внешнее давление, производимое поршнем, передается во все точки воды одинаково, и она выплескивается в виде одинаковых струек. Поэтому струйки, вытекающие из отверстий, расположенных в горизонтальной плоскости, оставляют на полу следы равной длины.
Факторы, влияющие на показатель
На давление жидкости могут влиять:
- ее плотность;
- атмосферное давление;
- температура;
- глубина сосуда;
- площадь дна сосуда.
Давление на дно и стенку сосуда
Закон Паскаля утверждает, что давление в любом месте покоящейся жидкости или газа по всем направлениям одинаково, причем оно одинаково передается по всему объему вещества. Таким образом, разницы между давлением на дно и на стенку нет.
Расчет давления жидкости на дно и стенки сосуда
Чтобы найти давление на дно сосуда, нужно взять приведенное выше основное уравнение гидростатики и подставить туда глубину, плотность и атмосферное давление.
В случае стенок непосредственно прилагать эту формулу можно только к бесконечно малым горизонтальным полоскам на боковых стенках сосуда. Чтобы рассчитать давление на стенки, нужно суммировать давление на все горизонтальные элементы их поверхности, используя правила интегрального исчисления. Паскаль, проведя эти расчеты, доказал, что от формы сосуда давление жидкости не зависит.
Единицы измерения
В международной системе единиц давление измеряется в Паскалях. Один Паскаль равен силе в один ньютон, производящей равномерное давление на единицу поверхности в один метр. Но на практике часто используют такую единицу измерения, как атмосфера, равную 76 см ртутного столба при нулевой температуре по Цельсию.
Определение
Атмосфера – внесистемная единица измерения, которая примерно означает давление атмосферы Земли на уровне Мирового океана.
Формулы расчета
Для описания процессов в гидравлических прессах или любых других системах, в которых давление собственно жидкостей ничтожно мало по сравнению с передаваемым им извне, используется формула закона Паскаля:
(р = frac{F}{S}.)
F – сила, с которой происходит воздействие на поверхности сосуда, S – площадь этой поверхности.
В учебных задачах обычно опускают такой параметр, как атмосферное давление, и используют для расчетов формулу:
(р = rhos gs h.)
Можно вывести эту формулу для сосудов, имеющих форму прямой призмы или цилиндра, из закона Паскаля.
(m = rhos V = rhos Ss h)
Вес (Р = g s m = gs rhos Ss h.)
Вес столба, давящего на дно сосуда, равен силе, и тогда:
(р = frac{Р}{S} = gs rhos Ss frac{h}{S} = gs rhos h.)
Применение на практике
Для гидравлических механизмов, например, прессов, можно рассчитать пропорциональный изменению площади выигрыш в силе, зная, во сколько раз увеличивается площадь большего поршня по сравнению с меньшим.
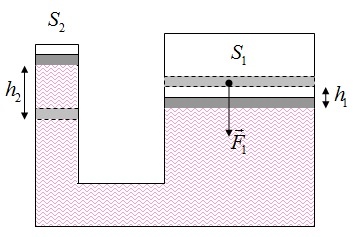
Соотношение между полезной и затраченной работой описывается понятием КПД, коэффициент полезного действия, и рассчитывается по формуле:
(frac{F_{2}h_{2}}{F_{1}h_{1}})
Также закон Паскаля описывает работу жидкостных манометров, приборов для измерения давления, отличного от атмосферного. Давление в одном колене манометра вызывает повышение жидкости в другом колене – это явление называется избыточным столбом. По его высоте, соотнося ее с нанесенной шкалой, пользователь прибора узнает точную цифру в миллиметрах ртутного столба.
Гидростатический парадокс
Согласно гидростатическому парадоксу, давление жидкости на любую плоскую стенку равняется весу столба этой жидкости, давящему на основание, площадь которого равна площади этой стенки. Поэтому от формы емкости давление не зависит. Если емкость расширяется к горлышку, то вес содержимого распределяется по наклонным стенкам и передается вниз через стенки, не давя на дно, а если емкость к горлышку сужается, то содержимое давит на стенки снизу вверх, что уменьшает его воздействие на дно.
Источник
Содержание:
- § 1 Особенности давления в жидкости и газе
- § 2 Формула для вычисления давления в жидкостях и газах
- § 3 Решение задачи по теме урока
- § 4 Краткие итоги по теме урока
§ 1 Особенности давления в жидкости и газе
Известно, что давление, производимое на жидкости и газы, передается в каждую точку без изменения по всем направлениям. Это утверждение называется законом Паскаля.
На жидкости, как и на все тела на Земле, действует сила тяжести. Поэтому верхние слои жидкости давят на нижележащие слои, это давление по закону Паскаля передается по всем направлениям. Значит, внутри жидкости существует давление. Чтобы убедиться в этом, поставим опыт.
Возьмем стеклянную трубочку, затянутую снизу резиновой пленкой. Если в трубочку нальем воду, то увидим, что резиновая пленка прогибается. На резиновую пленку действуют две силы: вес воды, направленный вниз, из-за чего пленка изменяет свою форму, и возникающая при деформации сила упругости, которая стремится восстановить первоначальную форму и направленная вверх. Если две эти силы равны, то пленка будет находиться в покое.
Опустим трубку с водой в другой, более широкий, сосуд с водой. Возникает третья сила, действующая на резиновую пленку, – сила давления воды снизу, она направлена вверх и заставляет пленку выпрямляться. Если уровни воды в трубке и в сосуде совпадут, то силы давления, действующие сверху и снизу на пленку, окажутся равными.
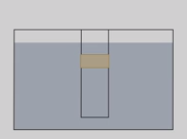
Такой же опыт проведем с трубкой, в которой есть боковое отверстие, затянутое резиновой пленкой. Если в трубку налить воду, то пленка выгибается наружу, так как вода давит не только на дно трубки, но и на стенки. Опустим трубку в воду и заметим, что пленка выпрямляется, то есть силы, действующие на пленку изнутри и снаружи, оказались равными.
Итак, опыты показывают, что внутри жидкости существует давление и на одном и том же уровне оно одинаково по всем направлениям.
Такое же утверждение справедливо и для газов.
§ 2 Формула для вычисления давления в жидкостях и газах
От чего зависит давление в жидкостях и газах?
Вспомним определение давления.
Давление – скалярная физическая величина, равная отношению силы, действующей перпендикулярно поверхности, к площади этой поверхности: p = F/S.
Сила давления Fравна весу P: P = mg.
Мы знаем, что массу тела можно найти по плотности вещества: m = ρV, где ρ – плотность, V – объем.
Объем жидкости, находящейся в сосуде в форме прямоугольного параллелепипеда или в форме цилиндра, можно найти, умножив площадь дна на высоту сосуда: V = Sh. Подставим формулы веса, массы, объема в формулу давления и, сократив площадь, получим:
Мы вывели формулу для вычисления давления в жидкостях и газах:
p = gρh.
Из этой формулы видно, что давление жидкости на дно сосуда зависит только от плотности и высоты столба жидкости.
По формуле p = gρhможно рассчитывать:
1)давление жидкости на дно в сосуде любой формы, то есть давление жидкости не зависит от формы сосуда;
2)давление жидкости на стенки сосуда, так как давление на одной и той же глубине одинаково по всем направлениям: вверх, вниз, вправо, влево, вперед, назад;
3)давление в газах.
Проверим единицу измерения давления по формуле p = gρh.
g – коэффициент тяжести, измеряется в Н/кг,
ρ – плотность, в международной системе единиц измеряется в кг/м3,
h – высота столба жидкости (глубина) – в м.
§ 3 Решение задачи по теме урока
Рассмотрим решение задачи:
Задача:Определить давление воды на дно морской впадины, глубина которой 10900 м. Плотность морской воды – 1030 кг/м3.
Решение: Запишем условие задачи: нам известны глубина h = 10900 м, плотность ρ = 1030 кг/м3. Необходимо найти: давление p. Для решения: запишем формулу расчета давления в жидкостях и газах p = gρh и подставим числовые значения:
p = 10 Н/кг · 1030 кг/м3· 10 900 м = 112 270 000 Па = 112, 27 МПа.

Ответ: 112, 27 МПа
§ 4 Краткие итоги по теме урока
ВАЖНО ЗАПОМНИТЬ:
На жидкости и газы действует сила тяжести, поэтому они обладают весом. Вышележащие слои жидкости и газа своим весом давят на нижележащие слои, то есть оказывают давление. Давление внутри жидкости и газа на одном и том же уровнеодинаково по всем направлениям.
Давление в жидкостях и газах рассчитывается по формуле p = gρh, где g – коэффициент тяжести, ρ – плотность, h – высота столба жидкости или газа.
Давление в жидкостях и газах зависит только от плотности и высоты столба жидкости или газа и не зависит от формы и площади поперечного сечения сосуда, в котором находится жидкость или газ.
Список использованной литературы:
- Волков В.А. Поурочные разработки по физике: 7 класс. – 3-е изд. – М.: ВАКО, 2009. – 368 с.
- Волков В.А. Тесты по физике: 7-9 классы. – М.: ВАКО, 2009. – 224 с. – (Мастерская учителя физики).
- Кирик Л.А. Физика -7. Разноуровневые самостоятельные и контрольные работы. М.: Илекса, 2008. – 192 с.
- Контрольно-измерительные материалы. Физика: 7 класс / Сост. Зорин Н.И. – М.: ВАКО, 2012. – 80 с.
- Марон А.Е., Марон Е.А. Физика. 7 Дидактические материалы. – М.: Дрофа, 2010. – 128 с.
- Перышкин А.В. Физика. 7 класс – М.: Дрофа, 2011.
- Тихомирова С.А. Физика в пословицах и поговорках, стихах и прозе, сказках и анекдотах. Пособие для учителя. – М.: Новая школа, 2002. – 144 с.
- Я иду на урок физики: 7 класс. Часть III: Книга для учителя. – М.: Издательство «Первое сентября”, 2002. – 272 с.
Источник
