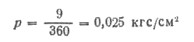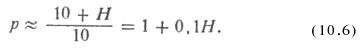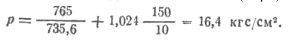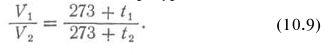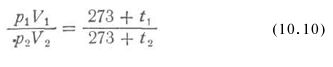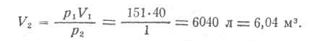Вычисление давления в сосуде

Давление является одним из трех основных термодинамических макроскопических параметров любой газовой системы. В данной статье рассмотрим формулы давления газа в приближении идеального газа и в рамках молекулярно-кинетической теории.
Идеальные газы
Каждый школьник знает, что газ является одним из четырех (включая плазму) агрегатных состояний материи, в котором частицы не имеют определенных положений и движутся хаотичным образом во всех направлениях с одинаковой вероятностью. Исходя из такого строения, газы не сохраняют ни объем, ни форму при малейшем внешнем силовом воздействии на них.
В любом газе средняя кинетическая энергия его частиц (атомов, молекул) больше, чем энергия межмолекулярного взаимодействия между ними. Кроме того, расстояния между частицами намного превышают их собственные размеры. Если молекулярными взаимодействиями и размерами частиц можно пренебречь, тогда такой газ называется идеальным.
В идеальном газе существует лишь единственный вид взаимодействия – упругие столкновения. Поскольку размер частиц пренебрежимо мал в сравнении с расстояниями между ними, то вероятность столкновений частица-частица будет низкой. Поэтому в идеальной газовой системе существуют только столкновения частиц со стенками сосуда.
Все реальные газы с хорошей точностью можно считать идеальными, если температура в них выше комнатной, и давление не сильно превышает атмосферное.
Причина возникновения давления в газах
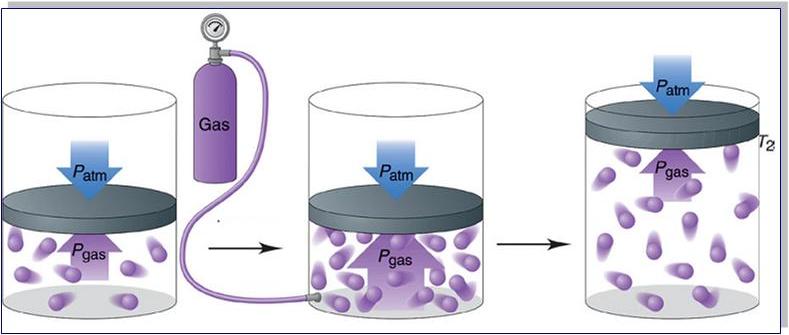
Прежде чем записать формулы расчета давления газа, необходимо разобраться, почему оно возникает в изучаемой системе.
Согласно физическому определению, давление – это величина, равная отношению силы, которая перпендикулярно воздействует на некоторую площадку, к площади этой площадки, то есть:
P = F/S
Выше мы отмечали, что существует только один единственный тип взаимодействия в идеальной газовой системе – это абсолютно упругие столкновения. В результате них частицы передают количество движения Δp стенкам сосуда в течение времени соударения Δt. Для этого случая применим второй закон Ньютона:
F*Δt = Δp
Именно сила F приводит к появлению давления на стенки сосуда. Сама величина F от столкновения одной частицы является незначительной, однако количество частиц огромно (≈ 1023), поэтому они в совокупности создают существенный эффект, который проявляется в виде наличия давления в сосуде.
Формула давления газа идеального из молекулярно-кинетической теории
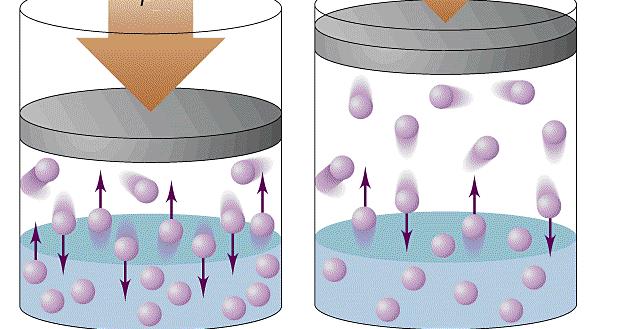
При объяснении концепции идеального газа выше были озвучены основные положения молекулярно-кинетической теории (МКТ). Эта теория основывается на статистической механике. Развита она была во второй половине XIX века такими учеными, как Джеймс Максвелл и Людвиг Больцман, хотя ее основы заложил еще Бернулли в первой половине XVIII века.
Согласно статистике Максвелла-Больцмана, все частицы системы движутся с различными скоростями. При этом существует малая доля частиц, скорость которых практически равна нулю, и такая же доля частиц, имеющих огромные скорости. Если вычислить среднюю квадратичную скорость, то она примет некоторую величину, которая в течение времени остается постоянной. Средняя квадратичная скорость частиц однозначно определяет температуру газа.
Применяя приближения МКТ (невзаимодействующие безразмерные и хаотично перемещающиеся частицы), можно получить следующую формулу давления газа в сосуде:
P = N*m*v2/(3*V)
Здесь N – количество частиц в системе, V – объем, v – средняя квадратичная скорость, m – масса одной частицы. Если все указанные величины определены, то, подставив их в единицах СИ в данное равенство, можно рассчитать давление газа в сосуде.
Формула давления из уравнения состояния

В середине 30-х годов XIX века французский инженер Эмиль Клапейрон, обобщая накопленный до него экспериментальный опыт по изучению поведения газов во время разных изопроцессов, получил уравнение, которое в настоящее время называется универсальным уравнением состояния идеального газа. Соответствующая формула имеет вид:
P*V = n*R*T
Здесь n – количество вещества в молях, T – температура по абсолютной шкале (в кельвинах). Величина R называется универсальной газовой постоянной, которая была введена в это уравнение русским химиком Д. И. Менделеевым, поэтому записанное выражение также называют законом Клапейрона-Менделеева.
Из уравнения выше легко получить формулу давления газа:
P = n*R*T/V
Равенство говорит о том, что давление линейно возрастает с температурой при постоянном объеме и увеличивается по гиперболе с уменьшением объема при постоянной температуре. Эти зависимости отражены в законах Гей-Люссака и Бойля-Мариотта.
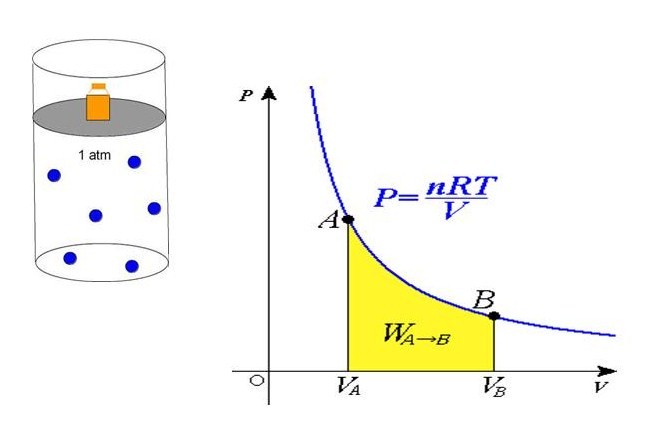
Если сравнить это выражение с записанной выше формулой, которая следует из положений МКТ, то можно установить связь между кинетической энергией одной частицы или всей системы и абсолютной температурой.
Давление в газовой смеси
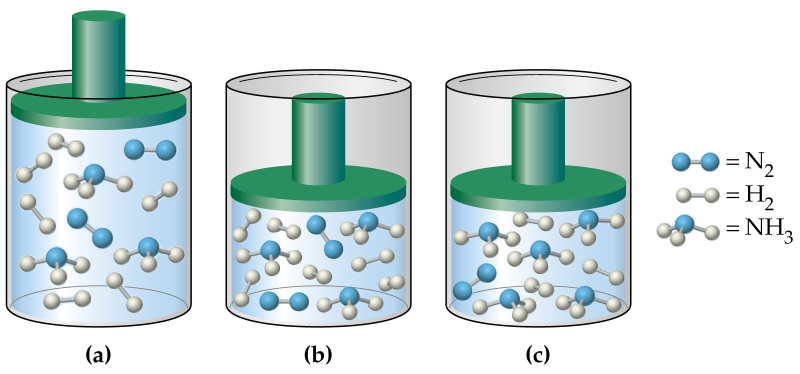
Отвечая на вопрос о том, как найти давление газа и формулы, мы ничего не говорили о том, является ли газ чистым, или речь идет о газовой смеси. В случае формулы для P, которая следует из уравнения Клапейрона, нет никакой связи с химическим составом газа, в случае же выражения для P из МКТ эта связь присутствует (параметр m). Поэтому при использовании последней формулы для смеси газов становится непонятным, какую массу частиц выбирать.
Когда необходимо рассчитать давление смеси идеальных газов, следует поступать одним из двух способов:
- Рассчитывать среднюю массу частиц m или, что предпочтительнее, среднее значение молярной массы M, исходя из атомных процентов каждого газа в смеси;
- Воспользоваться законом Дальтона. Он гласит, что давление в системе равно сумме парциальных давлений всех ее компонентов.
Пример задачи
Известно, что средняя скорость молекул кислорода составляет 500 м/с. Необходимо определить давление в сосуде объемом 10 литров, в котором находится 2 моль молекул.
Ответ на задачу можно получить, если воспользоваться формулой для P из МКТ:
P = N*m*v2/(3*V)
Здесь содержатся два неудобных для выполнения расчетов параметра – это m и N. Преобразуем формулу следующим образом:
m = M/NA;
n = N/NA;
m*N = M*n;
P = M*n*v2/(3*V)
Объем сосуда в кубических метрах равен 0,01 м3. Молярная масса молекулы кислорода M равна 0,032 кг/моль. Подставляя в формулу эти значения, а также величины скорости v и количества вещества n из условия задачи, приходим к ответу: P = 533333 Па, что соответствует давлению в 5,3 атмосферы.
Источник
Баннер Главный инструмент
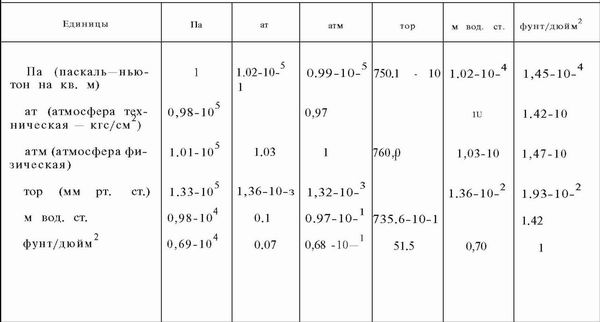
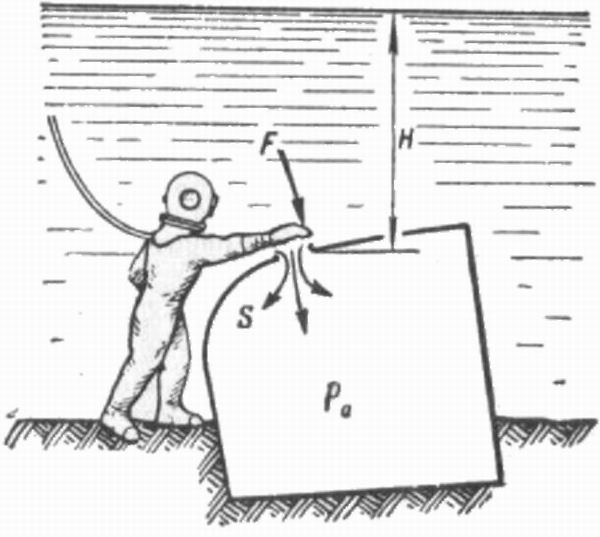
| Главная / Издания / Литература / Книжная полка / Справочник водолаза В водолазной практике часто приходится встречаться с В системах СИ и МКС единицей давления служит Механическое давление измеряется силой, действующей  где р — давление, кгс/см2; Пример 10.1. Определить давление, которое водолаз оказывает р = 180/360 = 0.5 кгс/см или в единицах СИ р = 0,5 * 0,98.105 = 49000 Па = 49 кПа. Таблица 10.1. | |||||||||
Источник
Содержание:
- § 1 Особенности давления в жидкости и газе
- § 2 Формула для вычисления давления в жидкостях и газах
- § 3 Решение задачи по теме урока
- § 4 Краткие итоги по теме урока
§ 1 Особенности давления в жидкости и газе
Известно, что давление, производимое на жидкости и газы, передается в каждую точку без изменения по всем направлениям. Это утверждение называется законом Паскаля.
На жидкости, как и на все тела на Земле, действует сила тяжести. Поэтому верхние слои жидкости давят на нижележащие слои, это давление по закону Паскаля передается по всем направлениям. Значит, внутри жидкости существует давление. Чтобы убедиться в этом, поставим опыт.
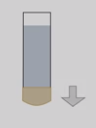
Возьмем стеклянную трубочку, затянутую снизу резиновой пленкой. Если в трубочку нальем воду, то увидим, что резиновая пленка прогибается. На резиновую пленку действуют две силы: вес воды, направленный вниз, из-за чего пленка изменяет свою форму, и возникающая при деформации сила упругости, которая стремится восстановить первоначальную форму и направленная вверх. Если две эти силы равны, то пленка будет находиться в покое.
Опустим трубку с водой в другой, более широкий, сосуд с водой. Возникает третья сила, действующая на резиновую пленку, – сила давления воды снизу, она направлена вверх и заставляет пленку выпрямляться. Если уровни воды в трубке и в сосуде совпадут, то силы давления, действующие сверху и снизу на пленку, окажутся равными.
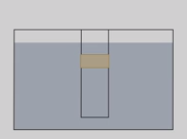
Такой же опыт проведем с трубкой, в которой есть боковое отверстие, затянутое резиновой пленкой. Если в трубку налить воду, то пленка выгибается наружу, так как вода давит не только на дно трубки, но и на стенки. Опустим трубку в воду и заметим, что пленка выпрямляется, то есть силы, действующие на пленку изнутри и снаружи, оказались равными.
Итак, опыты показывают, что внутри жидкости существует давление и на одном и том же уровне оно одинаково по всем направлениям.
Такое же утверждение справедливо и для газов.
§ 2 Формула для вычисления давления в жидкостях и газах
От чего зависит давление в жидкостях и газах?
Вспомним определение давления.
Давление – скалярная физическая величина, равная отношению силы, действующей перпендикулярно поверхности, к площади этой поверхности: p = F/S.
Сила давления Fравна весу P: P = mg.
Мы знаем, что массу тела можно найти по плотности вещества: m = ρV, где ρ – плотность, V – объем.
Объем жидкости, находящейся в сосуде в форме прямоугольного параллелепипеда или в форме цилиндра, можно найти, умножив площадь дна на высоту сосуда: V = Sh. Подставим формулы веса, массы, объема в формулу давления и, сократив площадь, получим:
![]()
Мы вывели формулу для вычисления давления в жидкостях и газах:
p = gρh.
Из этой формулы видно, что давление жидкости на дно сосуда зависит только от плотности и высоты столба жидкости.
По формуле p = gρhможно рассчитывать:
1)давление жидкости на дно в сосуде любой формы, то есть давление жидкости не зависит от формы сосуда;
2)давление жидкости на стенки сосуда, так как давление на одной и той же глубине одинаково по всем направлениям: вверх, вниз, вправо, влево, вперед, назад;
3)давление в газах.
Проверим единицу измерения давления по формуле p = gρh.
g – коэффициент тяжести, измеряется в Н/кг,
ρ – плотность, в международной системе единиц измеряется в кг/м3,
h – высота столба жидкости (глубина) – в м.
![]()
§ 3 Решение задачи по теме урока
Рассмотрим решение задачи:
Задача:Определить давление воды на дно морской впадины, глубина которой 10900 м. Плотность морской воды – 1030 кг/м3.
Решение: Запишем условие задачи: нам известны глубина h = 10900 м, плотность ρ = 1030 кг/м3. Необходимо найти: давление p. Для решения: запишем формулу расчета давления в жидкостях и газах p = gρh и подставим числовые значения:
p = 10 Н/кг · 1030 кг/м3· 10 900 м = 112 270 000 Па = 112, 27 МПа.

Ответ: 112, 27 МПа
§ 4 Краткие итоги по теме урока
ВАЖНО ЗАПОМНИТЬ:
На жидкости и газы действует сила тяжести, поэтому они обладают весом. Вышележащие слои жидкости и газа своим весом давят на нижележащие слои, то есть оказывают давление. Давление внутри жидкости и газа на одном и том же уровнеодинаково по всем направлениям.
Давление в жидкостях и газах рассчитывается по формуле p = gρh, где g – коэффициент тяжести, ρ – плотность, h – высота столба жидкости или газа.
Давление в жидкостях и газах зависит только от плотности и высоты столба жидкости или газа и не зависит от формы и площади поперечного сечения сосуда, в котором находится жидкость или газ.
Список использованной литературы:
- Волков В.А. Поурочные разработки по физике: 7 класс. – 3-е изд. – М.: ВАКО, 2009. – 368 с.
- Волков В.А. Тесты по физике: 7-9 классы. – М.: ВАКО, 2009. – 224 с. – (Мастерская учителя физики).
- Кирик Л.А. Физика -7. Разноуровневые самостоятельные и контрольные работы. М.: Илекса, 2008. – 192 с.
- Контрольно-измерительные материалы. Физика: 7 класс / Сост. Зорин Н.И. – М.: ВАКО, 2012. – 80 с.
- Марон А.Е., Марон Е.А. Физика. 7 Дидактические материалы. – М.: Дрофа, 2010. – 128 с.
- Перышкин А.В. Физика. 7 класс – М.: Дрофа, 2011.
- Тихомирова С.А. Физика в пословицах и поговорках, стихах и прозе, сказках и анекдотах. Пособие для учителя. – М.: Новая школа, 2002. – 144 с.
- Я иду на урок физики: 7 класс. Часть III: Книга для учителя. – М.: Издательство «Первое сентября”, 2002. – 272 с.
Источник