Вычислить теплоемкость газа заключенного в сосуд
двухатомного газа
Задача 10131
Определить молярную массу М двухатомного газа и его удельные теплоемкости, если известно, что разность cp–cv удельных теплоемкостей этого газа равна 260 Дж/(кг·К).
Задача 10134
В сосуде вместимостью V = 6 л находится при нормальных условиях двухатомный газ. Определить теплоемкость Cv этого газа при постоянном объеме.
Задача 10613
Вычислить теплоемкость при постоянном объеме двухатомного газа, заключенного в сосуд V = 10 л при нормальных условиях.
Задача 10615
Смесь состоит из двух молей одноатомного газа и одного моля двухатомного газа. Определить мольные теплоемкости CV и Ср смеси.
Задача 20495
Сосуд, содержащий газ, движется со скоростью v0, затем быстро останавливается. На сколько увеличится при этом средний квадрат скорости теплового движения молекул газа в случаях: а) одноатомного газа? б) двухатомного газа? Газ считать идеальным.
Задача 50451
Идеальный двухатомный газ совершает цикл, состоящий из двух изотерм и двух изохор, причем наибольшая температура газа 600 К, а наименьшая 300 К, наибольший объем 8 л, а наименьший 2 л. Найти КПД цикла и изменение энтропии в каждом процессе и за весь цикл для 1 моля газа.
Задача 50453
Построить два графика: а) изохоры для некоторой массы двухатомного газа; б) изохоры для этого же газа при условии, что при некоторой температуре Т1 каждая вторая молекула распалась на атомы.
Задача 14766
Плотность некоторого двухатомного газа при нормальных условиях ρ = 1,43 кг/м3. Найти удельные теплоемкости этого газа при постоянном объеме и постоянном давлении.
Задача 50489
Два идеальных газа, занимающих один и тот же начальный объём при одинаковом начальном давлении, внезапно подвергают адиабатному сжатию, каждый до половины его первоначального объёма. Найти отношение работ, необходимых для сжатия, если первый газ одноатомный, второй газ двухатомный.
Задача 14765
Удельная теплоемкость некоторого двухатомного газа ср = 14,7 кДж/(кг·К). Найти молярную массу μ этого газа.
Задача 26308
0,4 кг двухатомного газа находятся под давлением 2 атм и имеют плотность 4 кг/м3. Найти энергию поступательного и вращательного движения молекул газа при этих условиях.
Задача 11624
Идеальный двухатомный газ, содержащий количество вещества ν = 1 кмоль, совершает замкнутый цикл, график которого изображен на рис. 11.4. Определить: 1) количество теплоты Q1, полученное от нагревателя; 2) количество теплоты Q2, переданное охладителю; 3) работу А, совершаемую газом за цикл; 4) термический КПД η цикла.
Задача 13860
1 кг двухатомного газа находится под давлением 8·104 Па и имеет плотность 4 кг/м3. Найти энергию теплового движения молекул газа при этих условиях.
Задача 13872
При адиабатическом сжатии 1 кмоль двухатомного газа выполняется работа, равная 146 кДж. Насколько повысилась температура при сжатии газа?
Задача 14038
Идеальный двухатомный газ в количестве ν = 1 моль сначала изотермически расширился (Т1 = 300 К). Затем газ нагрели, повысив давление в 3 раза. Чему равна работа за весь процесс? Представьте график процесса в координатах P-V.
Задача 17291
Определить изменение энтропии ΔS двухатомного газа в количестве ν = 5,0 моль, если газ изобарно нагрели так, что его температура увеличилась в N = 4,0 раза. Колебательные степени свободы не учитывать.
Задача 17481
Определить плотность потока тепла, переносимого некоторым двухатомным газом при градиенте температуры 200 К/м, если при изотермическом увеличении объема 0,1 кг этого газа при Т = 400 К совершается работа А = 5,5 кДж, а коэффициент вязкости η = 5,5 мкПа·с.
Задача 17627
Идеальный двухатомный газ объемом 5 л и давлением 106 Па изохорически нагрели, в результате чего средняя кинетическая энергия его молекул увеличилась от 0,0796 эВ до 0,0923 эВ. На сколько при этом измениться давление газа? В дальнейшем газ изотермически расширили до начального давления. Определите объем газа в конце процесса.
Задача 19513
В результате адиабатического расширения двух молей некоторого двухатомного газа его объем увеличился в два раза. Работа внешних сил по расширению газа А = 3 кДж. Рассчитать отношение коэффициента теплопроводности к коэффициенту диффузии в начальном состоянии, если Р1 = 0,2 МПа.
Задача 20650
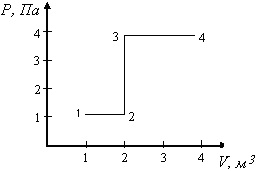
При переходе из состояния 1 в состояние 2 у двухатомного газа внутренняя энергия изменяется на … МДж.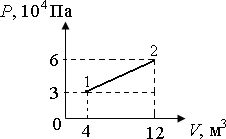
Задача 20656
При переходе из состояния 1 в состояние 4 отношение количества теплоты Q14, полученного двухатомным газом к работе A14, совершенной газом в этом процессе, Q14/A14 равно … .
Задача 20712
Двухатомный газ в количестве ν = 102 моль занимает объем V1 = 0,5 л, при давлении Р1 = 50 кПа. Газ сжимается адиабатически до некоторого объема V2 и давления Р2. Затем он охлаждается при постоянном объеме до первоначальной температуры, причем его давление становится равным Р3 = 100 кПа. Постройте график этого процесса в координатах Р–V, предварительно вычислив параметры второго состояния Р2, V2 (в конце адиабатического сжатия) и параметр V3 конечного состояния. Вычислите работу, совершенную газом за весь процесс.
Источник
Решение задач дело полезное, но не всегда интересное. Чтобы вы справлялись с решением задач по теме «Теплоемкость идеального газа» быстрее, приведем здесь несколько примеров и вопросов с объяснениями.
Подписывайтесь на наш телеграм-канал, чтобы получать полезную и интересную рассылку.
Задачи по теме «Теплоемкость идеального газа» с решениями
Повторение и практика – залог успеха в любом деле. И решение задач не исключение. Поэтому не забываем держать под рукой памятку по задачам и полезные формулы
Задача №1. Определить удельную теплоемкость идеального газа
Условие
Определить молярную массу M двухатомного газа и его удельные теплоемкости, если известно, что разность cр – cv удельных теплоемкостей этого газа равна 260 Дж/(кг*К)
Решение
По определению:
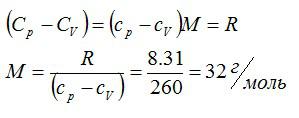
Значит, газ из задачи – кислород. Если кто не понял, как это определяется, учитесь пользоваться таблицей Менделеева.
Считаем удельные теплоемкости:
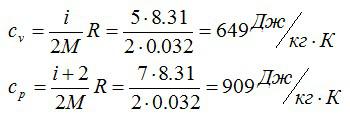
Ответ: 32 г/моль; 649 Дж/кг*К; 909 Дж/кг*К.
Задача №2. Удельная теплоемкость
Условие
Плотность некоторого газа при нормальных условиях ρ = 1,25 кг/м3. Отношение удельных теплоемкостей γ = 1,4. Определить удельные теплоемкости cv и сp этого газа.
Решение
Исходя из отношения удельных теплоемкостей, можно сделать вывод, что газ – двухатомный, i=5. При постоянном объеме удельная теплоемкость равна:
Молярную массу можно найти из уравнения Клапейрона-Менделеева:
Отсюда:
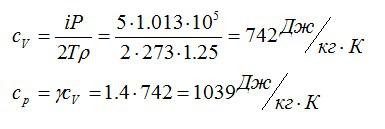
Ответ: 742 Дж/кг*К; 1039 Дж/кг*К.
Задача №3. Молярная теплоемкость
Условие
Вычислить молярные теплоемкости газа, зная, что его молярная масса М = 4∙10 3 кг/моль и отношение удельных теплоемкостей ср/сv = 1,67.
Решение
Удельные теплоемкости равны:
Можно найти:

Ответ: 12,4 Дж/моль*К; 20,71 Дж/моль*К
Задача №4. Теплоемкость при изопроцессах
Условие
На рисунке изображен изотермический процесс с газом постоянной массы. Сравните теплоемкость в процессе АВ с теплоемкостью этой же массы газа в изохорном процессе.
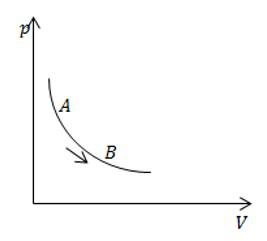
Решение
Теплоемкость при изохорном процессе является постоянной величиной. При изотермическом процесса она равна бесконечности. Значит, теплоемкость в процессе АВ больше.
Ответ: Теплоемкость в процессе АВ больше.
Задача №5. Теплоемкость при политропическом процессе
Условие
Найдите молярную теплоемкость идеального газа при политропическом процессе pVn = const, если показатель адиабаты газа равен γ. При каких значениях показателя политропы n теплоемкость газа будет отрицательной?
Решение
Запишем первое начало термодинамики, выражения для работы и изменения внутренней энергии в политропическом процессе соответственно:
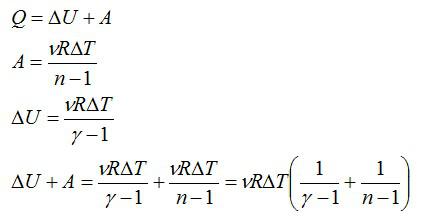
Если количество вещества и изменение температуры принять равными единице, это выражение будет равно молярной теплоемкости (по определению теплоемкости):
Ответ: см. выражение выше.
Вопросы по теме «Теплоемкость идеального газа»
Вопрос 1. Что такое теплоемкость идеального газа?
Ответ. Когда газу сообщается определенное количество теплоты, меняется его температура.
Отношение количества теплоты, сообщенного газу, к изменению его температуры, называется теплоемкостью идеального газа.
Вопрос 2. Что такое молярная и удельная теплоемкость идеального газа?
Ответ. Молярная и удельная теплоемкости активно используются в термодинамике. Молярная теплоемкость – это теплоемкость одного моля вещества.
Удельная теплоемкость – теплоемкость единичной массы вещества.
Вопрос 3. Как определяется теплоемкость газа при изопроцессах?
Ответ.
При изотермическом процессе T=const. Теплоемкость равна плюс/минус бесконечности.
При адиабатном процессе нет теплообмена с окружающей средой, теплоемкость равна нулю.
При изохорном процессе газ не совершает работы, а теплоемкость равна:
Здесь i – количество степеней свободы молекул газа. Для одноатомных газов i=3, для двухатомных i=5.
При изобарном процессе теплоемкость определяется соотношением Мейера:
Вопрос 4. Как еще связаны теплоемкости при постоянном давлении и постоянном объеме?
Ответ. Отношение теплоемкостей при постоянном давлении и постоянном объеме обозначается греческой буквой «гамма» и называется показателем адиабаты.
Вопрос 5. Как называются процессы, в которых теплоемкость газа остается неизменной?
Ответ. Такие процессы называются политропными. Адиабатный процесс – частный случай политропного процесса.
Теплоемкость реального газа не равна теплоемкости идеального газа и может сильно отличаться.
Нужна помощь в решении задач и выполнении других заданий? Специальный студенческий сервис готов оказать ее!
Источник
Примеры решения задач на удельные теплоемкости, (разные варианты).
1. Вычислить удельные теплоемкости при постоянном давлении и при постоянном объеме неона и водорода, принимая газы за идеальные.
Решение. Между молярными и удельными теплоемкостями идеального газа при постоянном давлениии и при постоянном объеме существует связь:
, а .
Таким образом, для удельныхтеплоемкостей имеем:
а .
Зная, что неон одноатомныйгаз длянего число степеней свободы i=3, m=20×10 -3 кг/моль, а водород двухатомный газ для него число степеней свободы i=5, m=27×10 -3 кг/моль. Подставляя в каждую из выше записанных формул значения и значение универсальной газовой постоянной R=8,31 Дж/(моль×К), вычисляем удельные теплоемкости для:
.
2. Найти отношение удельных теплоемкостей при постоянном давлении и постоянном объеме для кислорода.
Решение. Отношение удельных теплоемкостей при постоянном давлении и постоянном объеме идеального газа равно отношению его молярных теплоемкостей при постоянном давлении и постоянном объеме:
Зная, что молярные теплоемкости при постоянном давлении и при постоянном объеме связаны с числом степеней свободы и равны
и
Для отношения удельных теплоемкостей будем иметь
Кислород двухатомный газ, следовательно, число степеней свободы i=5. Подставляя значение i в вышезаписанную формулу, имеем:
3. Удельная теплоемкость некоторого двухатомного газа равна 14,7 кДж/(кг×К). Найти молярную массу этого газа.
Решение. Известно, что удельная теплоемкость при постоянном давлении связана с молярной теплоемкостью газа:
Молярная теплоемкость при постоянном давлении
где I – число степеней свободы газа.
Подставляяв полученную формулу значения данных в условии задачи величин, сучетом того, что для двухатомного газа i=5, будем иметь:
4. Вычислить удельные теплоемкости при постоянном объеме и постоянном давлении смеси неона и водорода, если массовые доли неона и водорода составляют w1=80% и w2=20% соответственно. Удельные теплоемкости для неона сv=6,24×10 2 Дж/(кг×К), сp==1,04×10 3 Дж/(кг×К); для водорода-сv=1,04×10 4 Дж/(кг×К), сp==1,46×10 4 Дж/(кг×К).
Решение. В общем случае количество тепла необходимого для нагревания смеси газов, например, при нагревании в условиях постоянного объема от температуры Т1 до температуры Т2 равна:
где сv(см) – удельная теплоемкость смеси;
С другой стороны это количество тепла может быть вычисленопо формуле:
где Q1 и Q1 – соответственно количество тепла, которое необходимо
сообщить, чтобы изменить температуру неона и водорода в отдельности;
сv1 и сv2 – удельные теплоемкости неона и водорода при постоянном объеме;
m1 и m2 – массы неона и водорода.
Таким образом имеем:
где
и – массовые доли неона и водорода соответственно.
Подставляячисленные значения для удельнойтеплоемкости смеси неона иводорода при постоянномдавлении, будемиметь:
Аналогично можно получить формулу для определения удельной теплоемкости смеси неона и водорода при постоянном давлении:
Подставляя численные значения для удельной теплоемкости смеси при постоянном давлении, будем иметь:
Источник
Вычислить теплоемкость при постоянном давлении двухатомного газа
Определить молярную массу М двухатомного газа и его удельные теплоемкости, если известно, что разность cp–cv удельных теплоемкостей этого газа равна 260 Дж/(кг·К).
В сосуде вместимостью V = 6 л находится при нормальных условиях двухатомный газ. Определить теплоемкость Cv этого газа при постоянном объеме.
Вычислить теплоемкость при постоянном объеме двухатомного газа, заключенного в сосуд V = 10 л при нормальных условиях.
Смесь состоит из двух молей одноатомного газа и одного моля двухатомного газа. Определить мольные теплоемкости CV и Ср смеси.
Сосуд, содержащий газ, движется со скоростью v, затем быстро останавливается. На сколько увеличится при этом средний квадрат скорости теплового движения молекул газа в случаях: а) одноатомного газа? б) двухатомного газа? Газ считать идеальным.
Идеальный двухатомный газ совершает цикл, состоящий из двух изотерм и двух изохор, причем наибольшая температура газа 600 К, а наименьшая 300 К, наибольший объем 8 л, а наименьший 2 л. Найти КПД цикла и изменение энтропии в каждом процессе и за весь цикл для 1 моля газа.
Построить два графика: а) изохоры для некоторой массы двухатомного газа; б) изохоры для этого же газа при условии, что при некоторой температуре Т1 каждая вторая молекула распалась на атомы.
Плотность некоторого двухатомного газа при нормальных условиях ρ = 1,43 кг/м 3 . Найти удельные теплоемкости этого газа при постоянном объеме и постоянном давлении.
Два идеальных газа, занимающих один и тот же начальный объём при одинаковом начальном давлении, внезапно подвергают адиабатному сжатию, каждый до половины его первоначального объёма. Найти отношение работ, необходимых для сжатия, если первый газ одноатомный, второй газ двухатомный.
Удельная теплоемкость некоторого двухатомного газа ср = 14,7 кДж/(кг·К). Найти молярную массу μ этого газа.
0,4 кг двухатомного газа находятся под давлением 2 атм и имеют плотность 4 кг/м 3 . Найти энергию поступательного и вращательного движения молекул газа при этих условиях.
Идеальный двухатомный газ, содержащий количество вещества ν = 1 кмоль, совершает замкнутый цикл, график которого изображен на рис. 11.4. Определить: 1) количество теплоты Q1, полученное от нагревателя; 2) количество теплоты Q2, переданное охладителю; 3) работу А, совершаемую газом за цикл; 4) термический КПД η цикла.
1 кг двухатомного газа находится под давлением 8·10 4 Па и имеет плотность 4 кг/м 3 . Найти энергию теплового движения молекул газа при этих условиях.
При адиабатическом сжатии 1 кмоль двухатомного газа выполняется работа, равная 146 кДж. Насколько повысилась температура при сжатии газа?
Идеальный двухатомный газ в количестве ν = 1 моль сначала изотермически расширился (Т1 = 300 К). Затем газ нагрели, повысив давление в 3 раза. Чему равна работа за весь процесс? Представьте график процесса в координатах P-V.
Определить изменение энтропии ΔS двухатомного газа в количестве ν = 5,0 моль, если газ изобарно нагрели так, что его температура увеличилась в N = 4,0 раза. Колебательные степени свободы не учитывать.
Определить плотность потока тепла, переносимого некоторым двухатомным газом при градиенте температуры 200 К/м, если при изотермическом увеличении объема 0,1 кг этого газа при Т = 400 К совершается работа А = 5,5 кДж, а коэффициент вязкости η = 5,5 мкПа·с.
Идеальный двухатомный газ объемом 5 л и давлением 10 6 Па изохорически нагрели, в результате чего средняя кинетическая энергия его молекул увеличилась от 0,0796 эВ до 0,0923 эВ. На сколько при этом измениться давление газа? В дальнейшем газ изотермически расширили до начального давления. Определите объем газа в конце процесса.
В результате адиабатического расширения двух молей некоторого двухатомного газа его объем увеличился в два раза. Работа внешних сил по расширению газа А = 3 кДж. Рассчитать отношение коэффициента теплопроводности к коэффициенту диффузии в начальном состоянии, если Р1 = 0,2 МПа.
При переходе из состояния 1 в состояние 2 у двухатомного газа внутренняя энергия изменяется на … МДж.
При переходе из состояния 1 в состояние 4 отношение количества теплоты Q14, полученного двухатомным газом к работе A14, совершенной газом в этом процессе, Q14/A14 равно . .
Двухатомный газ в количестве ν = 10 2 моль занимает объем V1 = 0,5 л, при давлении Р1 = 50 кПа. Газ сжимается адиабатически до некоторого объема V2 и давления Р2. Затем он охлаждается при постоянном объеме до первоначальной температуры, причем его давление становится равным Р3 = 100 кПа. Постройте график этого процесса в координатах Р–V, предварительно вычислив параметры второго состояния Р2, V2 (в конце адиабатического сжатия) и параметр V3 конечного состояния. Вычислите работу, совершенную газом за весь процесс.
Источник
Решение. Молярные теплоёмкости газа:
Молярные теплоёмкости газа:
, ,
где
– число степеней свободы молекул газа;
Дж/(моль∙К) – универсальная газовая постоянная.
Зная отношение теплоёмкостей, можем определить число степеней свободы газа:
;
;
.
Связь между удельной
и молярной теплоёмкостями:
,
где
– молярная теплоёмкость газа при постоянном объёме;
Найдём удельные теплоёмкости газа:
при постоянном объёме:
;
Дж/(кг∙К);
при постоянном давлении:
;
Дж/(кг∙К).
Ответ:
Дж/(кг∙К), Дж/(кг∙К).
18. Двухатомный газ под давлением р = 0,42 MПа и температуре
T ° = 20 ° С занимает объем V = 8 л. Определить теплоемкость Срэтого газа при постоянном давлении.
19. Одноатомный газ при нормальных условиях занимает объем V = 12 л. Вычислить теплоемкость Cnэтого газа при постоянном объеме.
20. Найти удельные сn, сри молярные Cn, Сртеплоемкости водорода и аргона.
21.Вычислить динамическую вязкость
кислорода при нормальных условиях.
22. Какова средняя арифметическая скорость á
ñ молекул кислорода при давлении р = 100 кПа, если известно, что средняя длина свободного пробега álñ молекулы кислорода при этих условиях равна 100 нм?
23. Найти среднее число ázñ столкновений молекулы хлора за время t = 1 c, если газ находится под давлением p = 1,5 кПа при температуре Т = 400 К.
24. При нормальных условиях длина свободного пробега álñ молекулы гелия равна 230 нм. Определить диаметр d молекулы гелия.
25. В сосуде объемом V = 2 л находится N = 4×10 22 молекул двухатомного газа. Найти коэффициент диффузии D газа при этих условиях, если коэффициент теплопроводности газа K=0,014 Вт/(м× К).
26. Кислород, находящийся под давлением р=133 Па, имеет среднюю арифметическую скорость á
ñ = 850 м/с. Вычислить среднее число ázñ столкновений молекулы кислорода при этих условиях за время t = 1 с.
27. Найти коэффициент теплопроводности К воздуха при температуре t ° = 10 °С и давлении р = 0,7 МПа. Диаметр d молекулы воздуха принять равным 3×10 -8 см .
Дата добавления: 2015-05-26 ; Просмотров: 646 ; Нарушение авторских прав?
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник
Источник
