Вычислите давление жидкости на дно сосуда

Æèäêîñòè (è ãàçû) ïåðåäàþò ïî âñåì íàïðàâëåíèÿì íå òîëüêî âíåøíåå äàâëåíèå, íî è òî äàâ­ëåíèå, êîòîðîå ñóùåñòâóåò âíóòðè íèõ áëàãîäàðÿ âåñó ñîáñòâåííûõ ÷àñòåé.

Äàâëåíèå, îêàçûâàåìîå ïîêîÿùåéñÿ æèäêîñòüþ, íàçûâàåòñÿ ãèäðîñòà­òè÷åñêèì.

Ïîëó÷èì ôîðìóëó äëÿ ðàñ÷åòà ãèäðîñòàòè÷åñêîãî äàâëåíèÿ æèäêîñòè íà ïðîèçâîëüíîé ãëóáèíå h (â îêðåñòíîñòè òî÷êè A íà ðèñóíêå).

Ñèëà äàâëåíèÿ, äåéñòâóþùàÿ ñî ñòîðîíû âûøåëåæàùåãî óçêîãî ñòîëáà æèäêîñòè, ìîæåò áûòü âûðàæåíà äâóìÿ ñïîñîáàìè:

1) êàê ïðîèçâåäåíèå äàâëåíèÿ p â îñíîâàíèè ýòîãî ñòîëáà íà ïëîùàäü åãî ñå÷åíèÿ S:

2) êàê âåñ òîãî æå ñòîëáà æèäêîñòè, ò. å. ïðîèçâåäåíèå ìàññû m æèäêîñòè íà óñêîðåíèå ñâî­áîäíîãî ïàäåíèÿ:

F=mg.                                  (1.28)

Ìàññà æèäêîñòè ìîæåò áûòü âûðàæåíà ÷åðåç åå ïëîòíîñòü p è îáúåì V:

m = pV,                                  (1.29)

à îáúåì — ÷åðåç âûñîòó ñòîëáà è ïëîùàäü åãî ïîïåðå÷íîãî ñå÷åíèÿ:

V=Sh.                                     (1.30)

Ïîäñòàâëÿÿ â ôîðìóëó (1.28) çíà÷åíèå ìàññû èç (1.29) è îáúåìà èç (1.30), ïîëó÷èì:

F = pVg=pShg.                           (1.31)

Ïðèðàâíèâàÿ âûðàæåíèÿ (1.27) è (1.31) äëÿ ñèëû äàâëåíèÿ, ïîëó÷èì:

pS = pSkg.

Ðàçäåëèâ îáå ÷àñòè ïîñëåäíåãî ðàâåíñòâà íà ïëîùàäü S, íàéäåì äàâëåíèå æèäêîñòè íà ãëóáèíå h:

p = phg.

Ýòî è åñòü ôîðìóëà ãèäðîñòàòè÷åñêîãî äàâëåíèÿ.

Ãèäðîñòàòè÷åñêîå äàâëåíèå íà ëþáîé ãëóáèíå âíóòðè æèäêîñòè íå çàâèñèò îò ôîðìû ñîñóäà, â êîòîðîì íàõîäèòñÿ æèäêîñòü, è ðàâíî ïðîèçâåäåíèþ ïëîòíîñòè æèäêîñòè, óñêîðåíèÿ ñâîáîäíî­ãî ïàäåíèÿ è ãëóáèíû, íà êîòîðîé îïðåäåëÿåòñÿ äàâëåíèå.

Âàæíî åùå ðàç ïîä÷åðêíóòü, ÷òî ïî ôîðìóëå ãèäðîñòàòè÷åñêîãî äàâëåíèÿ ìîæíî ðàññ÷èòûâàòü äàâëåíèå æèäêîñòè, íàëèòîé â ñîñóä ëþáîé ôîðìû, â òîì ÷èñëå, äàâëåíèå íà ñòåíêè ñîñóäà, à òàê­æå äàâëåíèå â ëþáîé òî÷êå æèäêîñòè, íàïðàâëåííîå ñíèçó ââåðõ, ïîñêîëüêó äàâëåíèå íà îäíîé è òîé æå ãëóáèíå îäèíàêîâî ïî âñåì íàïðàâëåíèÿì.

Ãèäðîñòàòè÷åñêèé ïàðàäîêñ .

Ãèäðîñòàòè÷åñêèé ïàðàäîêñ — ÿâëåíèå, çàêëþ÷àþùååñÿ â òîì, ÷òî âåñ æèäêîñòè, íàëèòîé â ñîñóä, ìîæåò îòëè÷àòüñÿ îò ñèëû äàâëåíèÿ æèäêîñòè íà äíî ñîñóäà.

 äàííîì ñëó÷àå ïîä ñëîâîì «ïàðàäîêñ» ïîíèìàþò íåîæèäàííîå ÿâëåíèå, íå ñîîòâåòñòâóþùåå îáû÷íûì ïðåäñòàâëåíèÿì.

Òàê, â ðàñøèðÿþùèõñÿ êâåðõó ñîñóäàõ ñèëà äàâëåíèÿ íà äíî ìåíüøå âåñà æèäêîñòè, à â ñóæà­þùèõñÿ — áîëüøå.  öèëèíäðè÷åñêîì ñîñóäå îáå ñèëû îäèíàêîâû. Åñëè îäíà è òà æå æèäêîñòü íàëèòà äî îäíîé è òîé æå âûñîòû â ñîñóäû ðàçíîé ôîðìû, íî ñ îäèíàêîâîé ïëîùàäüþ äíà, òî, íåñìîòðÿ íà ðàçíûé âåñ íàëèòîé æèäêîñòè, ñèëà äàâëåíèÿ íà äíî îäèíàêîâà äëÿ âñåõ ñîñóäîâ è ðàâíà âåñó æèäêîñòè â öèëèíäðè÷åñêîì ñîñóäå.

Ýòî ñëåäóåò èç òîãî, ÷òî äàâëåíèå ïîêîÿùåéñÿ æèäêîñòè çàâèñèò òîëüêî îò ãëóáèíû ïîä ñâîáîäíîé ïîâåðõíîñòüþ è îò ïëîòíîñòè æèäêîñòè: p = pgh (ôîðìóëà ãèäðîñòàòè÷åñêîãî äàâëåíèÿ æèäêîñòè). À òàê êàê ïëîùàäü äíà ó âñåõ ñîñóäîâ îäèíàêîâà, òî è ñèëà, ñ êîòîðîé æèäêîñòü äàâèò íà äíî ýòèõ ñîñó­äîâ, îäíà è òà æå. Îíà ðàâíà âåñó âåðòèêàëüíîãî ñòîëáà ABCD æèäêîñòè: P = oghS, çäåñü S — ïëîùàäü äíà (õîòÿ ìàññà, à ñëåäîâàòåëüíî, è âåñ â ýòèõ ñîñóäàõ ðàçëè÷íû).

Ãèäðîñòàòè÷åñêèé ïàðàäîêñ îáúÿñíÿåòñÿ çàêîíîì Ïàñêàëÿ — ñïîñîá­íîñòüþ æèäêîñòè ïåðåäàâàòü äàâëåíèå îäèíàêîâî âî âñåõ íàïðàâëåíèÿõ.

Èç ôîðìóëû ãèäðîñòàòè÷åñêîãî äàâëåíèÿ ñëåäóåò, ÷òî îäíî è òî æå êîëè÷åñòâî âîäû, íàõîäÿñü â ðàçíûõ ñîñóäàõ, ìîæåò îêàçûâàòü ðàçíîå äàâ­ëåíèå íà äíî. Ïîñêîëüêó ýòî äàâëåíèå çàâèñèò îò âûñîòû ñòîëáà æèäêîñòè, òî â óçêèõ ñîñóäàõ îíî áóäåò áîëüøå, ÷åì â øèðîêèõ. Áëàãîäàðÿ ýòîìó äàæå íåáîëüøèì êîëè÷åñòâîì âîäû ìîæíî ñîçäàâàòü î÷åíü áîëüøîå äàâëå­íèå.  1648 ã. ýòî î÷åíü óáåäèòåëüíî ïðîäåìîíñòðèðîâàë Á. Ïàñêàëü. Îí âñòàâèë â çàêðûòóþ áî÷êó, íàïîëíåííóþ âîäîé, óçêóþ òðóáêó è, ïîäíÿâ­øèñü íà áàëêîí âòîðîãî ýòàæà, âûëèë â ýòó òðóáêó êðóæêó âîäû. Èç-çà ìàëîé òîëùèíû òðóáêè âîäà â íåé ïîäíÿëàñü äî áîëüøîé âûñîòû, è äàâëå­íèå â áî÷êå óâåëè÷èëîñü íàñòîëüêî, ÷òî êðåïëåíèÿ áî÷êè íå âûäåðæàëè, è îíà òðåñíóëà.

Поскольку на жидкость действует сила тяжести, жидкое вещество обладает весом. Вес — это сила, с которой оно давит на опору, т. е. на дно сосуда, в который налито. Закон Паскаля говорит: давление на жидкость передается в любую ее точку, не меняя своей силы. Как же рассчитать давление жидкости на дно и стенки сосуда? Будем разбираться в статье, используя наглядные примеры.

Опыт

Представим, что у нас есть цилиндрический сосуд, в который налита жидкость. Обозначим высоту слоя жидкости h, площадь дна сосуда — S, а плотность жидкости — ρ. Искомое давление — это P. Его вычисляют путем деления силы, действующей под углом 90° к поверхности, на площадь этой поверхности. В нашем случае поверхность — это дно емкости. P = F/S.

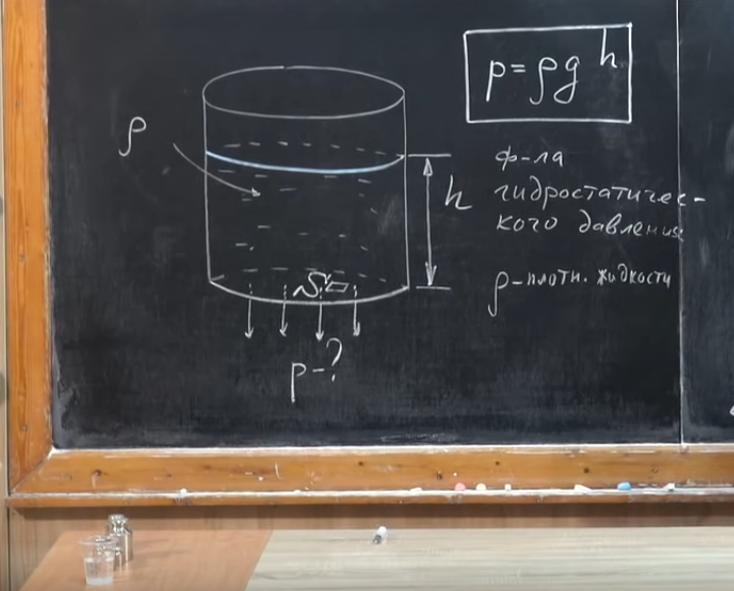
Сила давления жидкости на дно сосуда — это вес. Он равен силе давления. Наша жидкость неподвижна, поэтому вес равен силе тяжести (Fтяж ), действующей на жидкость, а значит, и силе давления (F=Fтяж). Fтяж находят так: умножают массу жидкости (m) на ускорение свободного падения (g). Масса может быть найдена, если известно, какова плотность жидкости и каков ее объем в сосуде. m = ρ×V. Сосуд имеет цилиндрическую форму, поэтому его объем мы будем находить, умножив площадь основания цилиндра на высоту слоя жидкости (V = S×h).

Расчет давления жидкости на дно сосуда

Вот величины, которые мы можем вычислить: V = S×h; m = ρ×V; F = m×g. Подставим их в первую формулу и получим такое выражение: P = ρ×S×h×g/S. Сократим площадь S, стоящую в числителе и знаменателе. Она исчезнет из формулы, а это значит, что давление на дно не зависит от площади сосуда. Кроме того, оно не зависит и от формы емкости.

Давление, которое жидкость создает на дно сосуда, называется гидростатическим. “Гидро” — это “вода”, а статическое — это потому, что жидкость неподвижна. По формуле, полученной после всех преобразований (P = ρ×h×g), определите давление жидкости на дно сосуда. Из выражения видно, что чем более плотная жидкость, тем больше ее давление на дно сосуда. Разберем подробнее, что собой представляет величина h.

Давление в толще жидкости

Допустим, мы нарастили сосуд снизу еще на некоторую величину, добавили дополнительное пространство для жидкости. Если мы поместим в емкость рыбку, давление на нее будет одинаковым в сосуде из предыдущего опыта и во втором, увеличенном? Изменится ли давление от того, что под рыбкой еще есть вода? Нет, потому что сверху находится определенный слой жидкости, на нее действует сила тяжести, значит, вода обладает весом. А то, что снизу, не имеет никакого значения. Следовательно, мы можем найти давление в самой толще жидкости, и h — это будет глубина. Она необязательно является расстоянием до дна, дно может быть и ниже.

Представим, что мы развернули рыбку на 90°, оставив ее на той же глубине. Изменится ли от этого давление на нее? Нет, потому что на глубине оно одинаково во всех направлениях. Если мы приблизим рыбку прямо к стенке сосуда, изменится ли давление на нее, если она будет оставаться на той же глубине? Нет. Во всех случаях давление на глубине h будет вычисляться по той же формуле. Значит, эта формула позволяет найти давление жидкости на дно и стенки сосуда на глубине h, т. е. в толще жидкости. Чем глубже, тем оно больше.

Давление в наклонном сосуде

Представим, что у нас есть трубка длиной около 1 м. Мы налили в нее жидкость так, что она заполнена целиком. Возьмем точно такую же трубку, наполненную до краев, и разместим ее под наклоном. Сосуды одинаковы и заполнены одной и той же жидкостью. Следовательно, масса и вес жидкости и в первой, и во второй трубке равны. Будет ли одинаковым давление в точках, расположенных на дне этих емкостей? На первый взгляд кажется, что давление P1 равно P2, поскольку масса жидкостей одинакова. Предположим, что это так, и проведем эксперимент, чтобы проверить.

Соединим нижние части этих трубок маленькой трубочкой. Если наше предположение о том, что P1 = P2, верное, то перетечет ли куда-то жидкость? Нет, потому что на ее частицы будут действовать силы противоположного направления, которые будут компенсировать друг друга.

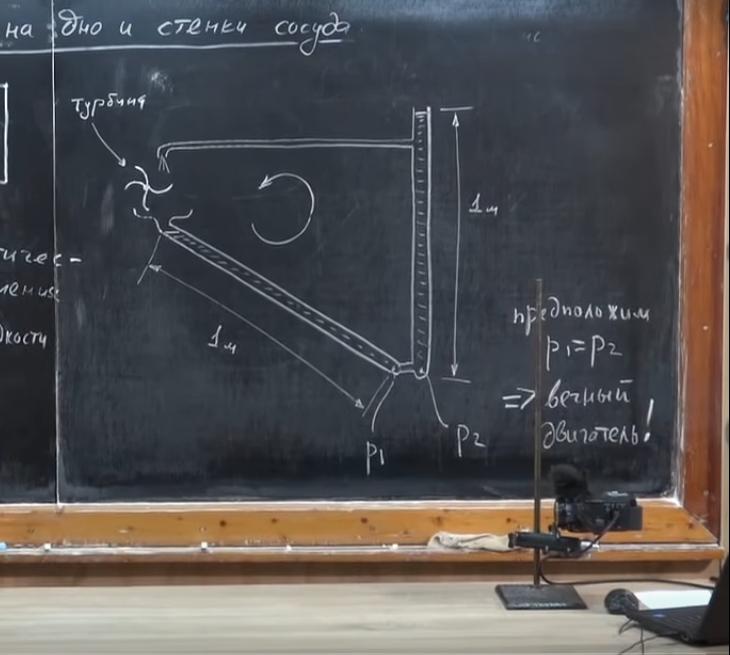
Давайте приделаем к наклонный трубке сверху воронку. А на вертикальной трубке проделаем отверстие, в него вставим трубочку, которая загибается вниз. Давление на уровне отверстия больше, чем на самом верху. Значит, жидкость будет перетекать по тоненькой трубочке и наполнять воронку. Масса жидкости в наклонной трубке будет увеличиваться, жидкость потечет из левой трубки в правую, затем будет подниматься и циркулировать по кругу.

А теперь установим над воронкой турбину, которую соединим с электрическим генератором. Тогда эта система самостоятельно, без какого-либо вмешательства будет вырабатывать электроэнергию. Она будет работать без остановки. Казалось бы, это и есть «вечный двигатель». Однако еще в XIX веке Французская академия наук отказалась принимать любые подобные проекты. Закон сохранения энергии говорит о том, что создать «вечный двигатель» невозможно. Значит, наше предположение о том, что P1 = P2, неверное. На самом деле P1< P2. Как же тогда рассчитать давление жидкости на дно и стенки сосуда в трубке, которая расположена под наклоном?

Высота столба жидкости и давление

Чтобы это выяснить, проведем следующий мысленный эксперимент. Возьмем сосуд, наполненный жидкостью. Поместим в него две трубки из металлической сетки. Одну расположим вертикально, а другую – наклонно, таким образом, что ее нижний конец будет находиться на той же глубине, что и дно первой трубки. Поскольку емкости находятся на одинаковой глубине h, то давление жидкости на дно и стенки сосуда будет тоже одинаковым.

Теперь заделаем все отверстия в трубках. Из-за того, что они стали сплошными, давление в их нижних частях изменится? Нет. Хотя давление и одинаково, а сосуды равны по размеру, масса жидкости в вертикальной трубке меньше. Глубина, на которой находится нижняя часть трубки, называется высотой столба жидкости. Дадим определение данному понятию: это отсчитываемое по вертикали расстояние от свободной поверхности до данной точки жидкости. В нашем примере высота столба жидкости одинакова, поэтому и давление одинаково. В предыдущем опыте высота столба жидкости в правой трубке больше, чем в левой. Поэтому давление P1 меньше, чем P2.