Высота сосуда по объему и площади
4.2. Элементы гидростатики
4.2.5. Сообщающиеся сосуды
Сообщающимися называются сосуды, соединенные между собой каналом, заполненным жидкостью.
Для сообщающихся сосудов справедлив закон сообщающихся сосудов: высоты взаимно уравновешенных столбов разнородных жидкостей обратно пропорциональны плотностям этих жидкостей:
h1h2=ρ2ρ1,
где h1 — высота столба жидкости плотностью ρ1; h2 — высота столба жидкости плотностью ρ2.
Указанный закон справедлив в отсутствие сил поверхностного натяжения.
Если сообщающиеся сосуды заполнены однородной жидкостью
ρ1 = ρ2,
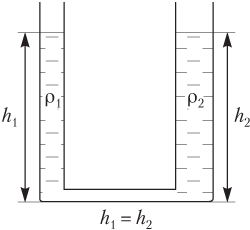
то свободные поверхности жидкости устанавливаются на одном уровне, независимо от формы сосудов (рис. 4.14):
h1 = h2,
где h1 — высота столба жидкости в левом колене; h2 — высота столба жидкости в правом колене сообщающихся сосудов.
Рис. 4.14
Если сообщающиеся сосуды заполнены разнородными жидкостями
ρ1 ≠ ρ2,
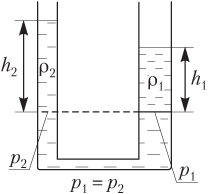
то свободные поверхности жидкостей, независимо от формы сосуда (рис. 4.15), устанавливаются так, что выполняется отношение
h1h2=ρ2ρ1,
где h1 — высота столба жидкости плотностью ρ1; h2 — высота столба жидкости плотностью ρ2.
Рис. 4.15
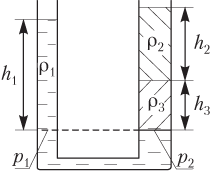
Если сообщающиеся сосуды заполнены несколькими жидкостями (например, как показано на рис. 4.16), то гидростатическое давление на одном уровне (отмеченном пунктиром) в левом колене определяется формулой
p1 = ρ1gh1,
в правом колене —
p2 = ρ2gh2 + ρ3gh3.
Рис. 4.16
Равенство давлений на указанном уровне
p1 = p2
позволяет записать тождество:
ρ1h1 = ρ2h2 + ρ3h3.
Пример 28. Два высоких сосуда, диаметр одного из которых в два раза больше диаметра второго, в нижней части соединены тонким шлангом. Площадь сечения узкого сосуда равна 10 см2. Система заполнена некоторым количеством жидкости плотностью 1,6 г/см3. Найти, на сколько миллиметров повысится уровень жидкости в каждом из сосудов, если в систему добавить 0,12 кг той же жидкости.
Решение. В сообщающихся сосудах однородная жидкость устанавливается на одном уровне.
Добавление в систему некоторого количества жидкости массой m приводит к ее распределению по двум сосудам в соответствии с площадью их поперечного сечения:
- в первом сосуде оказывается масса жидкости
m1 = ρV1 = ρ∆h1S1,
где ρ — плотность жидкости; V1 = S1∆h1 — объем жидкости в первом сосуде; S1 — площадь поперечного сечения первого сосуда; ∆h1 — повышение уровня жидкости в первом сосуде;
- во втором сосуде оказывается масса жидкости
m2 = ρV2 = ρ∆h2S2,
где V2 = S2∆h2 — объем жидкости во втором сосуде; S2 — площадь поперечного сечения второго сосуда; ∆h2 — повышение уровня жидкости во втором сосуде.
Повышение уровней жидкости в обоих сосудах одинаково:
∆h1 = ∆h2 = ∆h,
поэтому масса жидкости, добавленной в систему, определяется формулой
m = m1 + m2 = ρ∆h(S1 + S2).
Выразим отсюда искомое значение ∆h:
Δh=mρ(S1+S2).
Площади поперечного сечения сосудов связаны с их диаметрами формулой:
- для первого (широкого) сосуда
S1=πd124,
- для второго (узкого) сосуда
S2=πd224,
где d1 = 2d2 — диаметр первого (широкого) сосуда; d2 — диаметр второго (узкого) сосуда.
Отношение площадей
S1S2=πd1244πd22=d12d22=(d1d2)2=(2d2d2)2=4
позволяет найти площадь широкого сосуда:
S1 = 4S2.
Подставив S1 в формулу для ∆h
Δh=mρ(4S2+S2)=m5ρS2,
рассчитаем значение высоты, на которую повысится уровень жидкости в сосудах:
Δh=0,125⋅1,6⋅103⋅10⋅10−4=15⋅10−3 м=15 мм.
Пример 29. Два высоких сосуда, диаметр одного из которых в два раза больше диаметра другого, в нижней части соединены тонким шлангом. Площадь сечения широкого сосуда составляет 10 см2. Система заполнена жидкостью плотностью 6,0 г/см3. В узкий сосуд добавляют 0,12 кг жидкости плотностью 2,0 г/см3, а затем — 0,12 кг жидкости плотностью 4,0 г/см3. Найти разность уровней жидкостей в сосудах.
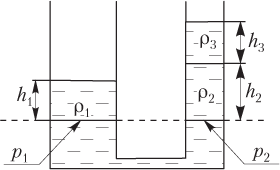
Решение. В сообщающихся сосудах неоднородная жидкость устанавливается на разных уровнях таким образом, что гидростатическое давление на выбранном уровне оказывается одинаковым:
p1 = p2,
где p1 — давление в широком сосуде; p2 — давление в узком сосуде.
На рисунке пунктирной линией обозначен уровень, на котором будем рассчитывать гидростатическое давление в широком и узком сосудах.
Гидростатическое давление на выбранном уровне:
- в широком сосуде
p1 = ρ1gh1,
где ρ1 — плотность жидкости, заполняющей систему изначально; g — модуль ускорения свободного падения; h1 — высота столба жидкости в широком сосуде;
- в узком сосуде
p2 = ρ2gh2 + ρ3gh3,
где ρ2 — плотность первой жидкости, добавленной в узкий сосуд; h2 — высота столба первой жидкости; ρ3 — плотность второй жидкости, добавленной в узкий сосуд; h3 — высота столба второй жидкости.
Равенство давлений на указанном уровне
ρ1gh1 = ρ2gh2 + ρ3gh3
позволяет определить высоту столба жидкости в широком сосуде:
h1=1ρ1(ρ2h2+ρ3h3),
где высоты жидкостей h2 и h3 определяются соответствующими массами и плотностями:
- для первой жидкости
h2=m2ρ2S2;
- для второй жидкости
h3=m3ρ3S2,
где S2 — площадь поперечного сечения узкого сосуда; m2 — масса первой жидкости, добавленной в узкий сосуд; m3 — масса второй жидкости, добавленной в узкий сосуд.
Подстановка h2 и h3 в формулу для h1 дает
h1=1ρ1(ρ2m2ρ2S2+ρ3m3ρ3S2)=m2+m3ρ1S2.
Площади поперечного сечения сосудов связаны с их диаметрами формулой:
- для широкого сосуда
S1=πd124,
- для узкого сосуда
S2=πd224,
где d1 = 2d2 — диаметр широкого сосуда; d2 — диаметр узкого сосуда.
Отношение площадей
S1S2=πd1244πd22=d12d22=(d1d2)2=(2d2d2)2=4
позволяет найти площадь узкого сосуда:
S2=S14.
Таким образом, высота столба жидкости в широком сосуде определяется выражением
h1=4(m2+m3)ρ1S1.
Высота столба жидкости над указанным уровнем в узком сосуде есть сумма:
h2+h3=m2ρ2S2+m3ρ3S2=4S1(m2ρ2+m3ρ3).
Искомая разность верхних уровней жидкостей в узком (h2 + h3) и широком h1 сосудах рассчитывается по формуле
Δh=(h2+h3)−h1=4S1(m2ρ2+m3ρ3)−4(m2+m3)ρ1S1=
=4S1(m2ρ2+m3ρ3−(m2+m3)ρ1).
Произведем вычисление:
Δh=410⋅10−4(0,122,0⋅103+0,124,0⋅103−0,12+0,126,0⋅103)=0,20 м=20 см.
Источник
Понятие объёма
Можно провести аналогию понятия объема сосуда с понятием площади. Напомним, что понятие площади применимо к плоскости. Любой многоугольник имеет свою площадь.
В качестве единицы измерения площади принято брать квадрат со стороной, равной единице. В случае объёма за единицу измерения берут куб с ребром, равным единице. Этот куб называют кубическим сантиметром (метром, миллиметром и т. д.) и обозначают $1 см^3$ (соответственно, $1 м^3, 1 мм^3$ и т.п.).
Другую аналогию между площадью и объёмом можно провести в самой процедуре их измерения. Объём выражается положительным числом, показывающим количество единиц измерения объёмов и частей, которые укладываются в данном теле. Число единиц объёма тела зависит от выбранной единицы измерения, то есть меняется в зависимости от того, выбраны $cм^3, м^3$ и т.п. Единицу измерения традиционно указывают после числа.
Приведём простейший пример. $V=3 мм^3$ – эта запись означает, что объём некоторого сосуда равен 3-м, если в качестве единицы измерения взят кубический миллиметр.
Основные свойства объёмов:
- У равных сосудов равные объёмы.
- В случае, когда сосуд состоит из нескольких сосудов, то его объём равен сумме всех этих сосудов.
Эти свойства аналогичны свойствам длин отрезков и площадей многоугольников.
Часто требуется найти объём параллелепипеда, пирамиды, цилиндра, конуса и шара. Параллельно с формулами объёма дадим ключевые определения. Чтобы рассмотреть такую фигуру как параллелепипед, необходимо дать два важных определения:
- Многогранник – это тело, ограниченное несколькими многоугольниками (гранями). Стороны граней называют рёбрами, а концы рёбер – вершинами.
- Призма – это многогранник, который составлен из двух параллельных многоугольников (оснований призмы), вершины которых соединены параллельными и равными друг другу отрезками (боковыми ребрами призмы), образующими параллелограммы (боковые грани призмы).
Нахождение объёма параллелепипеда
Параллелепипед – это многогранник, составленный из 6-ти прямоугольников. Или это четырёхугольная призма, в которой основания – параллелограммы. Форму параллелепипеда имеют коробки, комнаты и многие другие предметы из нашей повседневной жизни.
В случае, когда у параллелепипеда боковые ребра перпендикулярны к плоскостям оснований, а боковые грани и основания – прямоугольники, то этот параллелепипед называют прямоугольным (прямым).
Для нахождения объёма прямоугольного параллелепипеда необходимы его измерения. Измерения параллелепипеда – это длины трёх рёбер с общей вершиной. В речи мы называем измерениями “длину”, “ширину” и “высоту” (например, при измерении комнаты).
Определение 1
Объём прямоугольного параллелепипеда равен произведению трёх его измерений: $V=abc$.
Если площадь основания $S=ac$, а высота $h=b$, то формула объёма может быть следующей: $V=Sh$.
Нахождение объёма пирамиды
Пирамида – это многогранник, образованный из $n$-угольника (в качестве основания) и треугольников (в качестве боковых граней), построенных путем соединения одной точки (вершины пирамиды) отрезками (боковыми рёбрами) с вершинами многоугольника.
Рисунок 1. Пирамида. Автор24 — интернет-биржа студенческих работ
Определение 2
Объём пирамиды равен одной трети произведения площади основания на высоту. В данном случае высота представляет собой перпендикулярный к плоскости основания отрезок, который соединяет вершину пирамиды с плоскостью её основания.
$V=frac{Sh}{3}$.
Нахождение объёма цилиндра
Цилиндр – некоторое тело (или сосуд), полученное в результате вращения некоторого прямоугольника вокруг своей оси (одной из сторон прямоугольника).
Рисунок 2. Цилиндр. Автор24 — интернет-биржа студенческих работ
Определение 3
Объём цилиндра равен произведению площади основания на высоту: $V=Sh$.
Нахождение объёма конуса
Конус – это некоторое тело (сосуд), полученное в результате вращения прямоугольного треугольника вокруг его катета.
Рисунок 3. Конус. Автор24 — интернет-биржа студенческих работ
Определение 4
Объём конуса равен одной трети произведения площади основания на высоту: $V=frac{Sh}{3}$.
Нахождение объёма шара
Сфера – это поверхность, состоящая из всех точек пространства, расположенных на равном расстоянии (радиусе) от данной точки (центра).
Рисунок 4. Сфера. Автор24 — интернет-биржа студенческих работ
Шар – это некоторое тело (сосуд), которое ограничено сферой. Другой вариант определения: шар – это тело (сосуд), полученное в результате вращения полукруга вокруг диаметра этого полукруга.
Рисунок 5. Шар. Автор24 — интернет-биржа студенческих работ
Определение 5
Объём шара: $V=frac{4}{3}pi R^3$, где $R$ – радиус шара.
Таким образом, мы перечислили все основные формулы объёма основных фигур в стереометрии.
Источник
8. Геометрия в пространстве (стереометрия)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задание
8
#3045
Уровень задания: Равен ЕГЭ
Объем первого шара равен равен (54). Найдите объем второго шара, если его радиус в (3) раза меньше радиуса первого шара.
Объем шара радиуса (R) ищется по формуле (V=dfrac43 pi R^3). Следовательно, объем первого шара относится к объему второго как [dfrac{54}{V_2}=dfrac{V_1}{V_2}=
dfrac{frac43 pi ,R_1^3}{frac43 pi
,R_2^3}=left(dfrac{R_1}{R_2}right)^3] Так как радиус второго шара в 3 раза меньше радиуса первого шара, то (R_1=3R_2), следовательно, [dfrac{54}{V_2}=left(dfrac{3R_2}{R_2}right)^3=27 quadRightarrowquad
V_2=dfrac{54}{27}=2.]
Ответ: 2
Задание
9
#3053
Уровень задания: Равен ЕГЭ
Сосуд имеет форму конуса и вмещает в себя 2700 мл жидкости. Определите, сколько мл жидкости налито в сосуд, если высота жидкости в 3 раза меньше высоты сосуда.

Пусть (O) – центр основания большего конуса, (Q) – меньшего, а (S) – их общая вершина. В одной плоскости проведем радиусы (OA) и (QB), как показано на рисунке:
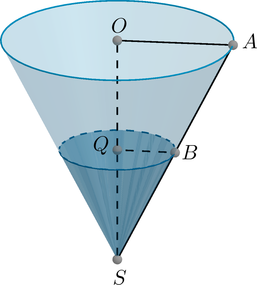
Тогда (QBparallel OA) и (triangle SQBsim triangle SOA). Следовательно, [dfrac{QB}{OA}=dfrac{QS}{OS}=dfrac13] Тогда объем налитой жидкости к объему всего сосуда относится как [dfrac{V_{small{text{ж}}}}{2700}=dfrac{V_{small{text{ж}}}}{V}=
dfrac{frac13cdot picdot QB^2cdot QS}{frac13cdot pi cdot
OA^2cdot OS}= left(dfrac{QB}{OA}right)^2cdot
dfrac{QS}{OS}=dfrac19cdot dfrac13=dfrac1{27}]
Следовательно объем жидкости равен [V_{small{text{ж}}}=dfrac1{27}V=100]
Ответ: 100
Задание
10
#3054
Уровень задания: Равен ЕГЭ
В сосуд цилиндрической формы, объем которого 2400 см(^3), налили жидкость, заполнив сосуд на треть, а затем в жидкость полностью погрузили некоторый предмет, вследствие чего уровень жидкости в сосуде поднялся на четверть. Найдите объем предмета в кубических сантиметрах.
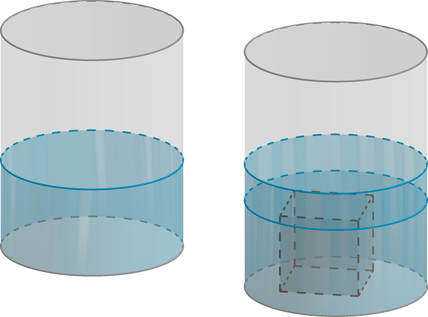
Объем цилиндра вычисляется по формуле (V=pi R^2H), где (R) – радиус основания, (H) – высота. Таким образом, во сколько раз увеличивается/уменьшается высота цилиндра, во столько же раз увеличивается/уменьшается объем цилиндра.
Следовательно, если жидкость заполнила сосуд лишь на треть, то есть высота жидкости в 3 раза меньше высоты сосуда, то и объем жидкости в 3 раза меньше объема сосуда, следовательно, объем жидкости равен (2400:3=800) см(^3).
Так как после погружения в жидкость предмета уровень повысился на четверть, то и занимаемый в сосуде объем повысился на четверть.
Закон Архимеда гласит, что объем вытесненной жидкости равен объему погруженного в нее предмета. Следовательно, объем предмета равен четверти объема жидкости, то есть (800:4=200) см(^3).
Ответ: 200
Задание
11
#3042
Уровень задания: Равен ЕГЭ
Радиус первого шара равен (6), а радиус второго шара равен (2). Во сколько раз объем первого шара больше объема второго шара?

Объем шара радиуса (R) ищется по формуле (V=dfrac43 pi R^3). Следовательно, объем первого шара относится к объему второго как [dfrac{V_1}{V_2}=dfrac{frac43 pi cdot 6^3}{frac43 pi cdot 2^3}=
left(dfrac62right)^3=27.] Следовательно, объем первого шара в 27 раз больше объема второго шара.
Ответ: 27
Задание
12
#3050
Уровень задания: Равен ЕГЭ
Объем первого цилиндра равен (16), причем известно, что его радиус в 7 раз меньше радиуса второго цилиндра, а высота второго цилиндра в 8 раз меньше высоты первого. Найдите объем второго цилиндра.
Объем цилиндра с высотой (H) и радиусом основания (R) ищется по формуле (V=pi R^2H). Тогда объем первого относится к объему второго цилиндра как [dfrac{16}{V_2}=dfrac{pi,R_1^2,H_1}{pi,R_2^2,H_2}=
left(dfrac{R_1}{R_2}right)^2cdot dfrac{H_1}{H_2}] Из условие следует, что (R_1=frac17R_2), (H_2=frac18H_1), следовательно, [dfrac{16}{V_2}=left(dfrac{frac17R_2}{R_2}right)^2cdot
dfrac{H_1}{frac18H_1}=dfrac1{49}cdot 8 quadRightarrowquad
V_2=98.]
Ответ: 98
Задание
13
#3052
Уровень задания: Равен ЕГЭ
В сосуд, имеющий форму конуса, налили 75 грамм жидкости до половины высоты сосуда. Сколько грамм этой же жидкости нужно долить в сосуд, чтобы заполнить его доверху?

Заметим, что из формулы физики (V=frac{m}{rho}) – объем равен отношению массы к плотности.
Пусть (O) – центр основания большего конуса, (Q) – меньшего, а (S) – их общая вершина. В одной плоскости проведем радиусы (OA) и (QB), как показано на рисунке:

Тогда (QBparallel OA) и (triangle SQBsim triangle SOA). Следовательно, [dfrac{OA}{QB}=dfrac{OS}{QS}=dfrac21] так как по условию высота жидкости в два раза меньше высоты сосуда. Тогда для жидкости имеем: [m_{small{text{ж}}}=V_{small{text{ж}}}cdot rho=
dfrac13cdot picdot QScdot QB^2 cdot rho] Следовательно, весь сосуд вмещает этой же жидкости [m=Vrho=dfrac13cdot picdot OScdot OA^2cdot rho=
dfrac 13cdot picdot 2QScdot (2QB)^2cdot rho= 8cdot
left(dfrac13cdot picdot QScdot QB^2cdot rhoright)=8cdot
75=600 {small{text{грамм}}}] Значит, долить нужно [600-75=525 {small{text{грамм}}}]
Заметим, что в данной задаче использование плотности – чистая формальность.
Ответ: 525
Задание
14
#3055
Уровень задания: Сложнее ЕГЭ
В правильной четырехугольной пирамиде с высотой (h) через точку на боковом ребре, лежащую на расстоянии (frac13h) от плоскости основания, проведена плоскость, параллельная плоскости основания, которая отсекает от пирамиды меньшую пирамиду. Найдите объем полученной меньшей пирамиды, если объем исходной пирамиды равен (54).
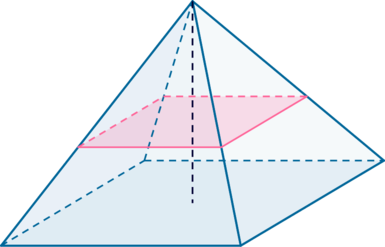
Пусть плоскость провели через точку (A’) на ребре (AS). Так как плоскость параллельна плоскости основания, то она пересечет боковые грани по прямым (A’B’, B’C’, C’D’, D’A’), параллельным соответственно (AB, BC, CD, DA), причем (SA’B’C’D’) – тоже правильная четырехугольная пирамида.
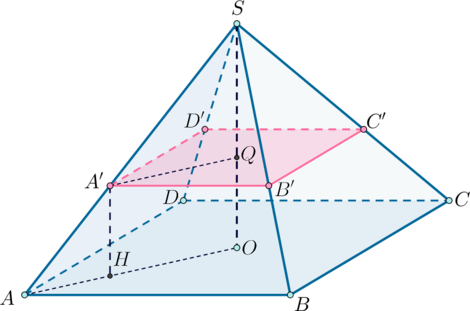
Рассмотрим плоскость (ASO). Проведем (A’Hparallel SO) ((SO) — высота исходной пирамиды). Тогда (A’Hperp ABC). Следовательно, это и есть расстояние, равное (frac13SO), на котором от плоскости основания проведена (розовая) плоскость.
(triangle AA’Hsim triangle ASO), следовательно, [dfrac{SA}{AA’}=dfrac{SO}{A’H}=3 quadRightarrowquad
SA=3AA’ quadRightarrowquad SA’=dfrac23SA] Также отсюда следует, что (SQ=frac23SO).
(triangle ASBsim triangle A’SB’), следовательно, [dfrac23=dfrac{SA’}{SA}=dfrac{A’B’}{AB} quadRightarrowquad
A’B’=dfrac23AB] Таким образом, объемы маленькой и большой пирамид относятся как [dfrac{V_{{small{text{м}}}}}{V_{small{text{б}}}}=
dfrac{frac13cdot SQcdot A’B’^2}{frac13cdot SOcdot
AB^2}=dfrac{SQ}{SO}cdot
left(dfrac{A’B’}{AB}right)^2=dfrac23cdot
left(dfrac23right)^2=dfrac8{27}] Следовательно, объем маленькой пирамиды равен [V_{{small{text{м}}}}=dfrac8{27}cdot 54=16.]
Ответ: 16
Источник