Высота столба жидкости в сосуде формула
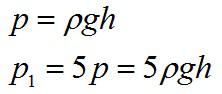
В последнее время мы разбирали решения многих простейших физических задач по разным темам: законы Ньютона, сила трения, свободное падение и т.д. Пришла пора взяться за что-то посложнее. Сегодня решаем задачи по теме «гидростатика».
За полезными лайфхаками и новостями студенческой жизни добро пожаловать на наш телеграм-канал.
Задачи по гидростатике с решениями
Задача №1 на гидростатику
Условие
B кувшине с водой плавает кусок льда. Как изменится уровень воды в сосуде, когда лед растает?
Решение
По условию плавания тел:
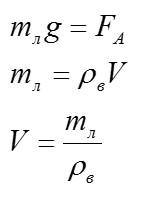
V – объем погруженной в воду части льда. После таяния льда образуется объем воды:
Как видим, объемы совпадают. Это значит, что при таянии льда его объем будет заменен таким же объемом воды.
Ответ: уровень не изменится.
Задача №2 на гидростатику
Условие
Кочан капусты массой 8 кг и объемом 10 л опускают в воду. Какой объем кочана окажется над водой?
Решение
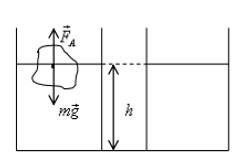
Кочан плавает на поверхности, на него действуют сила Архимеда и сила тяжести:
Здесь V – объем кочана, погруженный в воду. Чтобы узнать объем кочана над водой, нужно из общего объема вычесть погруженный:
В одном кубическом метре – тысяча литров.
Ответ: 2 литра.
Задача №3 на гидростатику
Условие
Каково давление на дне озера глубиной 5 м? Атмосферное давление принять равным 100 кПа.
Решение
Вспоминаем основное уравнение гидростатики и записываем:
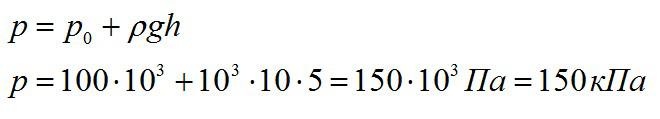
Ответ: 150 кПа.
Задача №4 на гидростатику
Условие
Вес тела в вакууме 2,6Н, в воде 1,6Н. Плотность воды 1000кг/м3. Определите плотность тела.
Решение
Вес – сила, с которой тело действует на опору. В воде вес меньше, так как на тело действует сила Архимеда, которая стремиться «поднять» его. В вакууме вес тела равен силе тяжести.
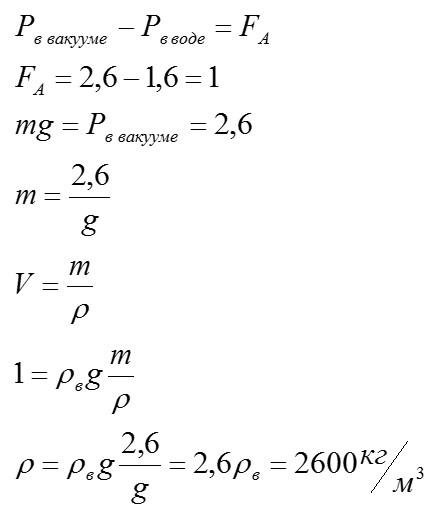
Ответ: 2600 кг/м3.
Задача №5 на гидростатику
Условие
Гидростатическое давление жидкости увеличилось в 5 раз. Как при этом изменилась высота столба жидкости в сосуде?
Решение
Формула для гидростатического давления:
Так как плотность жидкости и ускорение свободного падения остаются неизменными, можно сделать вывод, что высота столба жидкости увеличилась в пять раз.
Ответ: высота увеличилась в 5 раз.
Кстати! Для наших читателей действует скидка 10% на любой вид работы.
Вопросы по гидростатике
Вопрос 1. Что такое гидростатический парадокс?
Ответ. Гидростатический парадокс – явление, когда вес жидкости в сосуде не совпадает с весовым давлением, которое она оказывает на стенки сосуда. Возникает в сосудах конусообразной формы.
Вопрос 2. Какие есть внесистемные единицы изменения давления:
Ответ. Внесистемные единицы давления:
- миллиметр ртутного столба;
- бар;
- атмосфера.
Вопрос 3. В условиях физических задач часто можно встретить формулировку «нормальные условия». Что этот значить?
Ответ. Это значит, что давление нужно брать равным 101325 Па (или 760 мм рт. ст.), а температуру – 0 градусов Цельсия (или 273 Кельвина).
Вопрос 4. Что такое сообщающиеся сосуды?
Ответ. Сообщающиеся сосуды – это емкости, соединенные между собой. Жидкость может свободно перетекать из одного сосуда в другой. Уровень жидкости с одной плотностью в сообщающихся сосудах всегда одинаков. Простейший пример сообщающихся сосудов: обычный чайник. Если мы нальем в него воду, уровень будет одинаковым как в носике, так и в основном объеме. Если же плотности жидкостей разные, то выше будет уровень той, у которой плотность меньше.
Вопрос 5. Что такое гидравлический пресс?
Ответ. Гидравлический пресс – устройство, в основе действия которого лежит закон Паскаля и принцип сообщающихся сосудов. Пресс состоит из двух соединённых и заполненных маслом цилиндров: узкого и широкого. При нажатии на поршень узкого цилиндра, широкий цилиндр получает во столько раз большее давление, во сколько раз площадь большего поршня больше площади меньшего поршня.
Гидростатика: немного теории
Гидростатика – раздел физики, изучающий равновесие жидкостей.
Равновесие жидкостей – очень важный раздел. Например, если вы выпили много пива, просто необходимо, чтобы оно находилось в равновесии. Но шутки в сторону! Какие фундаментальные понятия нужно знать, чтобы решать задачи по гидростатике?
Давление и плотность
Давление – физическая величина, равная отношению модуля силы, перпендикулярно действующей на поверхность, к площади этой поверхности.
Давление столба жидкости называют гидростатическим, а измеряется оно в Паскалях. Гидростатическое давление столба жидкости высотой h на дно сосуда рассчитывается по формуле:
Греческое «ро» – плотность жидкости. Плотность измеряется в килограммах на кубический метр и равна отношению массы тела к его объему.
Жидкость – изотропная среда. Это значит, что ее свойства одинаковы в любой ее точке.
Закон Паскаля и основное уравнение гидростатики
Давление, оказываемое на жидкость или газ передается в любую точку этой жидкости одинаково и во всех направлениях.
Это и есть закон Паскаля. Согласно ему, давление жидкости зависит только от плотности жидкости и высоты ее столба. На глубине h жидкость оказывает одинаковое давление как на дно, так и на стенки сосуда.
В данном случае р нулевое – давление столба воздуха (атмосферы), которое действует на жидкость.
В своей другой формулировке основное уравнение гидростатики показывает, что гидростатический напор является постоянной величиной для всего объема неподвижной жидкости. Здесь мы не будем останавливаться на этом понятии, так как оно изучается в курсе гидравлики.
Закон Архимеда и условия плавания тел
Закон Архимеда – еще одна важнейшая часть гидростатики. Он гласит:
На тело, погруженное в газ или жидкость действует выталкивающая сила, равная весу жидкости (газа) в объеме погруженной части тела. Эта сила называется силой Архимеда.
Тело плавает, если выталкивающая сила Архимеда больше действующей на него силы тяжести. Это же условие можно переписать, используя понятие плотности: тело будет плавать, если плотность жидкости больше, чем плотность тела.
Подробнее о законе Архимеда и фактах из жизни этого выдающегося античного инженера читайте в нашем отдельном материале.
Нужна помощь в решении задач? Обращайтесь в профессиональный студенческий сервис за качественным и быстрым объяснением.
Источник
Давление
«Давление». Значит, что-то на что-то давит. То есть воздействует. Хм… Кажется, у нас уже была физическая величина, которая показывала, как интенсивно что-то действует на что-то другое. Какая это величина, как вы думаете?
Какая величина описывает интенсивность действия одного тела на другое?
Работа.
Сила.
Импульс.
Кинетическая энергия.
Давление. «Опять новая величина? А что, тех величин, которые уже есть, недостаточно? – резонно можете спросить вы. – У нас есть понятие силы для того, чтобы описывать, как и что действует на некоторое тело. Зачем ещё и давление?» Понять, зачем нужно давление, вам поможет следующий пример.
Представьте себе ситуацию: есть 101010 человек, и на них сверху опускают тяжеленную коробку массой в 500500500 килограмм.
Смогут ли они удержать такую коробку? Смогут. Почему?
Почему десять человек смогут удержать коробку массой 500500500 кг?
Потому что они сильны духом.
Потому что с ними бог.
Потому что на одного человека приходится небольшая масса в 505050 кг.
Потому что 500500500 кг легко удержит и один человек.
А смог ли бы удержать коробку массой 500500500 кг один человек? Нет, скорее всего – она бы его раздавила.
Отсюда мы можем сделать вывод, что имеет значение не только масса тела, не только сила тяжести тела, не только интенсивность воздействия – то есть сила FFF – но и то, как распределяется эта нагрузка. Если сила действует на некоторое тело, которое имеет некоторый размер, то логично, что будет иметь значение, на какую площадь SSS воздействует эта нагрузка.
Давление – величина, которая учитывает распределение воздействия некоторой силы FFF на некоторую площадь SSS.
Как вы думаете, как будет правильно в таком случае записать формулу для давления ppp? Выберите правильный вариант.
p=F−Sp = F – Sp=F−S.
p=FSp = frac{F}{S}p=SF.
p=SFp = frac{S}{F}p=FS.
p=FSp = FS p=FS.
Итак, запишем формулу давления:
p=FSp=frac{F}{S}p=SF.
Стоит отметить, что площадь SSS, которая входит в формулу давления, – это площадь соприкосновения предмета, «который давит», и предмета, «на который давят». Например, если человек идет по поверхности льда пруда площадью 400400400 кв. м., то в формулу давления, которое человек оказывает на лед, надо подставить площадь подошв его ботинок, а не всей поверхности пруда целиком.
Единица измерения давления – Паскаль:
[p]=[FS]=Ньютонметр2=Паскаль=Па [p] = [ frac{F}{S} ] =frac{Ньютон}{метр^2}= Паскаль = Па[p]=[SF]=метр2Ньютон=Паскаль=Па.
Разберем задачу.
Условие
Аквариум, изображённый на рисунке, доверху наполнили водой. Найдите давление воды на дно аквариума. Плотность воды равна ρrhoρ. Атмосферное давление не учитывать.
- ρgarho gaρga
- 2ρga32 rho g a^3 2ρga3
- Pg2a2frac{Pg}{2a^2}2a2Pg
- 2ρga2 rho ga 2ρga
(Источник: ЕГЭ-2013. Физика. Реальный экзамен. Урал. Вариант 1)
Решение
Шаг 1. Вспомним формулу давления.
Выберите правильную формулу для давления.
p=F−Sp = F – Sp=F−S
p=FSp = frac{F}{S}p=SF
p=SFp = frac{S}{F}p=FS
p=FSp = FS p=FS
Шаг 2. Определим, какая сила давит на дно сосуда.
Какая сила давит на дно сосуда?
сила тяжести воды
сила реакции опоры сосуда
сила трения воды о стенки сосуда
сила вязкого внутреннего трения жидкости
Шаг 3. Попробуем выразить силу тяжести через известные нам величины. Для начала просто запишем формулу силу тяжести.
Как можно вычислить силу тяжести воды?
F=mghF = mghF=mgh
F=mgF = mgF=mg
F=mgSF = frac{mg}{S}F=Smg
F=mgSF = mgSF=mgS
Шаг 4. В формуле F=mgF=mgF=mg нам неизвестна масса воды mmm. Ее можно выразить через другие величины, данные в условии.
Как можно вычислить силу тяжести, зная размеры сосуда и плотность?
F=mg=4ρa3gF = mg = 4 rho a^3 g F=mg=4ρa3g
F=mg=2ρagF = mg = 2 rho ag F=mg=2ρag
F=mg=ρagF = mg = rho ag F=mg=ρag
F=mg=ρgF = mg = rho g F=mg=ρg
Шаг 5. Вычислим давление по формуле p=FSp = frac{F}{S}p=SF.
Подставим в формулу давления ранее полученное выражение для силы:
p=FS=4ρa3g2a⋅a=2ρagp = frac{F}{S} = frac{4 rho a^3 g}{2a cdot a} = 2 rho agp=SF=2a⋅a4ρa3g=2ρag.
Правильный ответ: 4) 2ρga2 rho ga2ρga.
Давление столба жидкости
Представьте, что вы опустились со специальным аквалангом на дно озера.
Если вы поднимите голову вверх, то увидите, что над вами находится толща воды. Целый водяной столб. И он находится прямо над вами.
Как вы думаете, что он делает с вами?
Ничего не делает.
Выталкивает меня наверх.
Давит на меня.
Пытается сместить меня вбок.
На столб действует сила тяжести: F=mgF = mgF=mg.
Если площадь человека в поперечине равна SSS, то на человека будет оказываться давление: p=FS=mgSp = frac{F}{S} = frac{mg}{S} p=SF=Smg.
Массу жидкости можно расписать.
Как правильно расписать массу жидкости?
m=ρVm = rho Vm=ρV
m=ρVm = frac{rho}{V}m=Vρ
m=Vρm = frac{V}{rho}m=ρV
m=ρ+Vm = rho + Vm=ρ+V
Если представить, что столб жидкости – цилиндр высотой hhh и площадью поперечного сечения SSS, то его объём можно выразить через hhh и SSS.
Как можно записать объем столба жидкости? Выберите правильную формулу.
V=hSV = frac{h}{S}V=Sh
V=hSV = hS V=hS
V=h+SV = h + S V=h+S
V=ShV = frac{S}{h} V=hS
Тогда давление столба жидкости можно записать следующим образом: p=FS=mgS=ρhSgS=ρghp = frac{F}{S} = frac{mg}{S} = frac{rho hSg}{S} = rho gh p=SF=Smg=SρhSg=ρgh.
Итак, гидростатическое давление столба жидкости на глубине hhh рассчитывается по формуле p=ρgh.p = rho gh {.}p=ρgh.
Решим задачу.
Сосуд, изображённый на рисунке, доверху наполнили некоторой жидкостью. Найдите давление жидкости на дно сосуда. Плотность жидкости равна ρrhoρ. Атмосферное давление не учитывать.
(Источник: ЕГЭ-2013. Физика. Урал. Вариант 6)
2ρga32 rho g a^3 2ρga3
2ρga2 rho g a 2ρga
2ρga22 rho g a^2 2ρga2
ρga rho g a ρga
Гидростатика. Закон Паскаля
Раздел гидростатики в физике занимается давлениями неподвижных жидкостей. Нечто похожее у нас уже было в разделе «Статика», когда мы рассматривали неподвижность твёрдых тел, рассматривали правило моментов: чтобы вращающие моменты уравновешивали друг друга.
В гидростатике – нечто похожее: рассматриваются давления жидкости в условии, когда она неподвижна – то есть не течёт. Для этого раздела важен закон Паскаля:
Давление жидкости передаётся в любую точку без изменения во всех направлениях.
Сложная формулировка. Сложный закон. Понять его можно на примере. Возьмём полиэтиленовый пакет, нальём в него жидкость и сделаем несколько небольших дырочек. Будем давить сверху на этот пакет с жидкостью. Что мы увидим? Вода будет литься из каждой дырочки.
И можно заметить, что наше давление сверху на пакет будет передаваться без изменения в каждую «дырочку» пакета – струйки воды получатся примерно одинаковые, хоть и будут направлены в разные стороны.
Получается, что если до некоторой точки жидкости дошло давление, то давление от этой точки будет распространяться во все стороны.
На основе закона Паскаля основано действие различных гидравлических прессов и других механических устройств, в которых требуется передача давления чего-либо из одной точки – в другую точку (например – экскаватора, тормозной системы автомобилей). Такое устройство может представлять собой трубку, внутри которой находится жидкость. С одной стороны трубки – давят на жидкость, жидкость передаёт это давление – и давит на что-то с другого конца трубки.
Для того чтобы закон Паскаля стал вам окончательно понятен, приведём ещё один пример. Допустим, у нас есть палка. Просто палка. И мы давим этой палкой на землю. Действуем сверху вниз. Если земля не слишком твёрдая, то палка «уйдёт» у нас вниз. И только вниз. Ни вбок, ни вверх. Вниз.
Рассмотрим другой случай. Пусть у нас есть трубка, а на её конце – резиновый шарик. А внутри трубки и шарика – жидкость. Тогда, если мы будем давить на жидкость в трубке, то шарик у нас будет раздуваться во все стороны. Не только вниз, не только вбок – а во все стороны сразу. То есть давление в жидкости передаётся во все стороны, а давление в твёрдых телах – преимущественно в том направлении, в котором приложено давление.
Разберем задачу.
Условие
В широкую U-образную трубку с вертикальными прямыми коленами налиты неизвестная жидкость плотностью ρ1rho _1 ρ1 и вода плотностью ρ2=1,0⋅103 кг/м3rho _2 = 1,0 cdot 10^3text{ }кг/м^3 ρ2=1,0⋅103 кг/м3 (см. рисунок).
На рисунке b=10b = 10b=10 см, h=24h = 24h=24 см, H=30H = 30H=30 см. Чему равна плотность ρ1rho _1ρ1?
- 0,6⋅103 кг/м30,6cdot 10^3text{ }кг/м^30,6⋅103 кг/м3
- 0,7⋅103 кг/м30,7cdot 10^3text{ }кг/м^30,7⋅103 кг/м3
- 0,8⋅103 кг/м30,8cdot 10^3text{ }кг/м^30,8⋅103 кг/м3
- 0,9⋅103 кг/м30,9cdot 10^3text{ }кг/м^30,9⋅103 кг/м3
(Источник: сайт решуегэ.рф)
Решение
Шаг 1. В задаче даны плотности и высоты столбов жидкости. Определим тип этой задачи.
Как вы думаете, на что может быть эта задача?
на силы
на гидростатическое давление жидкостей
на уравнение моментов сил
на объёмы
Шаг 2. Так же, как в задачах на правило моментов вращающие моменты уравновешивают друг друга, в задачах на гидростатическое давление мы часто будем иметь дело с противодействием.
Кто кому в этой задаче противодействует?
Жидкости в левой части трубки противодействуют жидкости в правой части трубки.
Жидкость плотностью ρ1rho _1ρ1 противодействует жидкости плотностью ρ2rho _2ρ2.
Сила тяжести противодействует силе давления жидкости.
U-образная рубка противодействует жидкости.
Шаг 3. Определим, что оказывает давление в левой части трубки.
Что давит в левой части трубки?
жидкость ρ1rho _1ρ1 и небольшая часть жидкости ρ2rho _2ρ2
жидкость ρ1rho _1ρ1
жидкость ρ2rho _2ρ2
материал трубки
Шаг 4. Запишем условие равенства гидростатических давлений.
Как правильно записать условие равенства гидростатических давлений?
ρ1gH+ρ2gb=ρ2ghrho _1 gH + rho _2 gb = rho _2 ghρ1gH+ρ2gb=ρ2gh
ρ1g(H−b)+ρ2gb=ρ2ghrho _1 g(H – b) + rho _2 gb = rho _2 ghρ1g(H−b)+ρ2gb=ρ2gh
ρ1gH=ρ2gh+ρ2gbrho _1 gH = rho _2 gh + rho _2 gbρ1gH=ρ2gh+ρ2gb
ρ1g(H−b)=ρ2gh+ρ2gbrho _1 g(H – b) = rho _2 gh + rho _2 gbρ1g(H−b)=ρ2gh+ρ2gb
Шаг 5. Преобразуем выражение и подставим численные значения.
Для начала заметим, что можно сократить всё выражение на ускорение свободного падения ggg:
ρ1g(H−b)+ρ2gb=ρ2gh⇔ρ1(H−b)+ρ2b=ρ2hrho _1 g(H – b) + rho _2 gb = rho _2 ghLeftrightarrowrho _1(H – b) + rho _2 b = rho _2 hρ1g(H−b)+ρ2gb=ρ2gh⇔ρ1(H−b)+ρ2b=ρ2h.
В задаче просят найти плотность жидкости ρ1rho _1ρ1.
Сделаем это:
ρ1=ρ2h−ρ2bH−b=ρ2(h−b)H−b=ρ2h−bH−brho _1 = frac{rho _2 h – rho _2 b}{H – b} = frac{rho _2 (h – b)}{H – b} = rho _2 frac{h – b}{H – b}ρ1=H−bρ2h−ρ2b=H−bρ2(h−b)=ρ2H−bh−b.
Подставим численные значения:
ρ1=ρ2h−bH−b=1⋅103кгм3⋅24см−10см30см−10см=rho _1 = rho _2 frac{h – b}{H – b} = 1 cdot 10^3 frac{кг}{м^3} cdot frac{24 см – 10 см}{30 см – 10 см} =ρ1=ρ2H−bh−b=1⋅103м3кг⋅30см−10см24см−10см=
=103кгм3⋅0,7=700кгм3= 10^3 frac{кг}{м^3} cdot 0,7 = 700 frac{кг}{м^3}=103м3кг⋅0,7=700м3кг.
Правильный ответ: 2) 0,7⋅103 кг/м30,7 cdot 10^3text{ }кг/м^30,7⋅103 кг/м3.
Источник
Определение
Соединенные между собой сосуды называют сообщающимися.
В таких сосудах жидкость имеет возможность перетекать из одной емкости в другую (рис.1). Форма сообщающихся сосудов может быть самая разная.
Допустим, что в сообщающиеся сосуды налита однородная жидкость, то в этих сосудах жидкость устанавливается на одном уровне, если давление над поверхностью жидкости одинаково, и не важно какую форму имеют сосуды. В неподвижной жидкости давление ($p$) на одном уровне в сообщающихся сосудах является равным, так как мы знаем, что:
[p=rho gh left(1right),]
где $rho $ – плотность жидкости; $g$ – ускорение свободного падения; $h$ – высота столба жидкости. Так как давление на одном уровне жидкости одинаково, то равными будут и высоты столбов жидкости.
Жидкости разной плотности в сообщающихся сосудах
Допустим, что в сообщающиеся сосуды налили жидкость разной плотности (рис.2(б)). В состоянии равновесия жидкостей, их уровни не будут находиться на одном уровне (высоты столбов жидкости равными не будут).
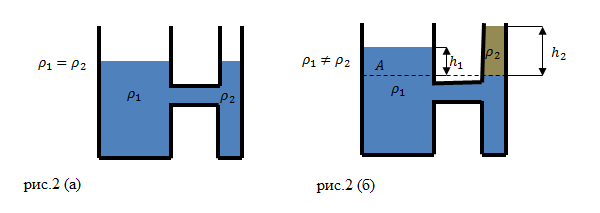
Жидкости в сосудах находятся в равновесии. Давления на уровне A (граница раздела разных жидкостей) (рис. 2 (б)) равны:
[{rho }_1gh_1={rho }_2gh_2left(2right),]
где ${rho }_1$ и ${rho }_2$ – плотности жидкостей. Найдем отношение высот столбов жидкостей в сосудах:
[frac{h_1}{h_2}=frac{{rho }_2}{{rho }_1}left(3right).]
Формула (3) говорит о том, что в сообщающихся сосудах высоты столбиков жидкости над уровнем их раздела обратно пропорциональны плотностям этих жидкостей. При одинаковом давлении над поверхностями жидкостей, высота столба жидкости с меньшей плотностью будет больше, чем высота столба более плотной жидкости.
Гидравлический пресс и другие примеры использования сообщающихся сосудов
В технике сообщающиеся сосуды используют часто. Например, существует такое устройство, как гидравлический пресс. Его изготавливают из двух цилиндров разного радиуса, в которых находятся поршни (рис.3). Сообщающиеся сосуды пресса обычно заполняют минеральным маслом.
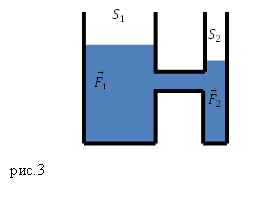
Пусть площадь первого поршня, к которому прикладывают силу ${overline{F}}_1,$ равна $S_1$, площадь второго $S_2$, к нему приложена сила ${overline{F}}_2$. Давление, которое создает первый поршень равно:
[p_1=frac{F_1}{S_1}left(4right).]
Второй поршень давит на жидкость:
[p_2=frac{F_2}{S_2}left(5right).]
Если система находится в состоянии равновесия, то по закону Паскаля давления $p_1$ и $p_2$ равны:
[frac{F_1}{S_1}=frac{F_2}{S_2}left(6right).]
Получим:
[F_1=F_2frac{S_1}{S_2}(7)]
величина первой силы больше модуля силы $F_2$ в $frac{S_1}{S_2}$ раз. Это означает, что при помощи гидравлического пресса, прикладывая небольшую силу к поршню малого сечения, можно получить большую по величине силу, которая будет действовать на большой поршень.
По принципу сообщающихся сосудов, в особенности раньше, действовал водопровод. Такой водопровод сейчас еще можно наблюдать на дачных участках. На относительно большой высоте устанавливается бак с водой, от бака идут водопроводные трубы, закрываемые кранами. Давление у кранов соответствует давлению столба воды, который равен разности высот уровень крана – уровень воды в баке.
Принципом сообщающихся сосудов пользовались, когда проектировали фонтаны, работающие без насосов, шлюзы на реках и каналах.
Примеры задач с решением
Пример 1
Задание. Имеются два цилиндрических сосуда. Высота столба жидкости в одном равна $h_1$, в другом $h_2$. Эти сосуды соединяют трубкой. Насколько изменится высота столба жидкости в левом сосуде, если площадь поперечного сечения его $S_1>S_2$ , $S_2$ – площадь сечения правого сосуда. Объемом трубки пренебречь.
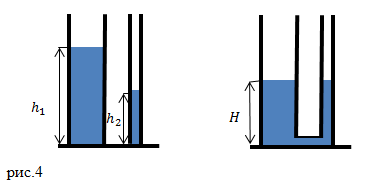
Решение. После того как сосуды соединили, они стали сообщающимися. Часть жидкости из левого сосуда перетечет в правый. Так как жидкость в правом и левом сосудах одна и та же, то уровни жидкости в обоих сосудах будут находиться на одном уровне, то есть высота столбиков жидкости станет равна $H$ в обоих коленах емкости. Определим, какой объем воды перетечет из левого колена в правое:
[Delta V_1=left(h_1-Hright)S_{1 }left(1.1right),]
где $S_{1 }$ – площадь поперечного сечения левого сосуда (сосуда из которого вытекает жидкость). В правом сосуде эта жидкость займет объем равный:
[Delta V_2=left(H-h_2right)S_{2 }left(1.2right),]
где $S_{2 }$ – площадь поперечного сечения правого сосуда. Так как мы считаем, что жидкость не сжимаема, то имеем:
[Delta V_1=Delta V_2left(1.3right).]
Приравниваем правые части выражений (1.2) и (1.1), выражаем высоту столбиков жидкости в правой и левой части сообщающихся сосудов:
[left(h_1-Hright)S_{1 }=left(H-h_2right)S_{2 }to H=frac{h_1S_{1 }+S_{2 }h_2}{S_1+S_{2 }} left(1.4right).]
Используя выражение (1.4), изменение высоты жидкости в левом колене, получим равным:
[Delta h=h_1-H=h_1-frac{h_1S_{1 }+S_{2 }h_2}{S_1+S_{2 }}=frac{h_1S_1+h_1S_2-h_1S_{1 }-S_{2 }h_2}{S_1+S_{2 }}=]
[=frac{h_1S_2-S_{2 }h_2}{S_1+S_{2 }}=frac{h_1-h_2}{S_1+S_{2 }}S_2.]
Ответ. $Delta h=frac{h_1-h_2}{S_1+S_{2 }}S_2$
Пример 2
Задание. Какой будет сила давления на большой поршень (площадью $S_1$) гидравлического пресса, если площадь его малого поршня равна $S_2$, при этом на него действует сила равная $F_2$?
Решение. В теоретическом разделе сказано, что гидравлический пресс представляет собой систему из сообщающихся сосудов (рис.3). Из закона Паскаля следует, что, прикладывая небольшую силу ($F_2$) к поршню малого сечения ($S_2$) пресса, можно получить большую по величине силу, которая будет действовать на большой поршень ($S_1$):
[F_1=F_2frac{S_1}{S_2}(2.1)]
Ответ. $F_1=F_2frac{S_1}{S_2}$
Читать дальше: условия плавания тел.
Источник
