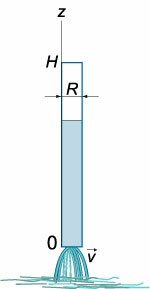
Вытекание воды из сосуда
|
Источник
Лекция 5. ИСТЕЧЕНИЕ ЖИДКОСТИ ИЗ ОТВЕРСТИЙ, НАСАДКОВ И ИЗ-ПОД ЗАТВОРОВ
Рассмотрим различные случаи истечения жидкости из резервуаров, баков, котлов через отверстия и насадки (коротки трубки различной формы) в атмосферу или пространство, заполненное газом или той же жидкость. В процессе такого истечения запас потенциальной энергии, которым обладает жидкость, находящаяся в резервуаре, превращается в кинетическую энергию свободной струи.
Основным вопросом, который интересует в данном случае, является определение скорости истечения и расхода жидкости для различных форм отверстий и насадков.
Рассмотрим большой резервуар с жидкостью под давлением Р0, имеющий малое круглое отверстие в стенке на достаточно большой глубине Н0 от свободной поверхности (рис.5.1).
Рис. 5.1. Истечение из резервуара через малое отверстие
Жидкость вытекает в воздушное пространство с давлением Р1. Пусть отверстие имеет форму, показанную на рис.5.2, а, т.е. выполнено в виде сверления в тонкой стенке без обработки входной кромки или имеет форму, показанную на рис.5.2, б, т.е. выполнено в толстой стенке, но с заострением входной кромки с внешней стороны. Струя, отрываясь от кромки отверстия, несколько сжимается (рис.5.2, а). Такое сжатие обусловлено движением жидкости от различных направлений, в том числе и от радиального движения по стенке, к осевому движению в струе.
Рис. 5.2. Истечение через круглое отверстие
Степень сжатия оценивается коэффициентом сжатия.
где Sс и Sо – площади поперечного сечения струи и отверстия соответственно; dс и dо – диаметры струи и отверстия соответственно.
Скорость истечения жидкости через отверстие такое отверстие
где Н – напор жидкости, определяется как
φ- коэффициент скорости
где α – коэффициент Кориолиса;
ζ- коэффициент сопротивления отверстия.
Расход жидкости определяется как произведение действительной скорости истечения на фактическую площадь сечения:
Произведение ε и φ принято обозначать буквой и называть коэффициентом расхода, т.е. μ = εφ.
В итоге получаем расход
где ΔР – расчетная разность давлений, под действием которой происходит истечение.
При помощи этого выражения решается основная задача – определяется расход.
Значение коэффициента сжатия ε, сопротивления ζ, скорости φ и расхода μ для круглого отверстия можно определить по эмпирически построенным зависимостям. На рис.5.3 показаны зависимости коэффициентов ε, ζ и μ от числа Рейнольдса, подсчитанного для идеальной скорости
где ν – кинематическая вязкость.
| Рис. 5.3. Зависимость ε, φ и от числа Reu | Рис. 5.4. Инверсия струй |
При истечении струи в атмосферу из малого отверстия в тонкой стенке происходит изменение формы струи по ее длине, называемое инверсией струи (рис.5.4). Обуславливается это явление в основном действием сил поверхностного натяжения на вытекающие криволинейные струйки и различными условиями сжатия по периметру отверстия. Инверсия больше всего проявляется при истечении из некруглых отверстий.
Несовершенное сжатие наблюдается в том случае, когда на истечение жидкости через отверстие и на формирование струи оказывает влияние близость боковых стенок резервуара (рис.5.5).
Рис. 5.5. Схема несовершенного сжатия струи
Так как боковые стенки частично направляют движение жидкости при подходе к отверстию, то струя по выходе из отверстия сжимается в меньшей степени, чем из резервуара неограниченных размеров, как это было описано в п.5.1.
При истечении жидкостей из цилиндрического резервуара круглого сечения через круглое отверстие, расположенное в центре торцевой стенки, при больших числах Re коэффициент сжатия для идеальной жидкости можно найти по формуле, представленной Н.Е. Жуковским:
где n – отношение площади отверстия Sо к площади поперечного сечения резервуара S1
Расход жидкости при несовершенном сжатии
где напор Н нужно находить с учетом скоростного напора в резервуаре
Часто приходится иметь дело с истечением жидкости не в атмосферу, а в пространство, заполненное этой же жидкостью (рис.5.6). такой случай называется истечением под уровень, или истечением через затопленное отверстие.
Рис. 5.6. Истечение по уровень
В этом случае вся кинетическая энергия струи теряется на вихреобразование, как при внезапном расширении.
Скорость истечения в сжатом сечении струи
где φ – коэффициент скорости;
Н – расчетный напор,
Расход жидкости равен
Таким образом, имеем те же расчетные формулы, что и при истечении в воздух (газ), только расчетный напор Н в данном случае представляет собой разность гидростатических напоров по обе стенки, т.е. скорость и расход жидкости в данном случае не зависят от высот расположения отверстия.
Коэффициенты сжатия и расхода при истечении под уровень можно принимать те же, что и при истечении в воздушную среду.
Внешним цилиндрическим насадком называется короткая трубка длиной, равной нескольким диаметрам без закругления входной кромки (рис. 5.7). На практике такой насадок часто получается в тех случаях, когда выполняют сверление в толстой стенке и не обрабатывают входную кромку. Истечение через такой насадок в газовую среду может происходить в двух режимах.
Первый режим – безотрывный режим. При истечении струя, после входа в насадок сжимается примерно так же, как и при истечении через отверстие в тонкой стенке. Затем струя постепенно расширяется до размеров отверстия из насадка выходит полным сечением (рис.5.7).
Рис. 5.7. Истечение через насадок
Коэффициент расхода μ, зависящий от относительной длины насадка l / d и числа Рейнольдса, определяется по эмпирической формуле:
Так как на выходе из насадка диаметр струи равен диаметру отверстия, то коэффициент сжатия ε = 1 и, следовательно, μ = φ , а коэффициент сопротивления ζ = 0,5.
Если составить уравнение Бернулли для сжатого сечения 1-1 и сечения за насадком 2-2 и преобразовать его, то можно получить падение давления внутри насадка
P2 – P1 0,75Hgρ
При некотором критическом напоре Нкр абсолютное давление внутри насадка (сечение 1-1) становится равным нулю (P1 = 0), и поэтому
Следовательно, при Н > Нкр давление P1 должно было бы стать отрицательным, но так как в жидкостях отрицательных давлений не бывает, то первый режим движения становится невозможным. Поэтому при Н Нкр происходит изменение режима истечения, переход от первого режима ко второму (рис.5.8).
Рис. 5.8. Второй режим истечения через насадок
Второй режим характеризуется тем, что струя после сжатия уже не расширяется, а сохраняет цилиндрическую форму и перемещается внутри насадка, не соприкасаясь с его стенками. Истечение становится точно таким же, как и из отверстия в тонкой стенке, с теми же значениями коэффициентов. Следовательно, при переходе от первого режима ко второму скорость возрастает, а расход уменьшается благодаря сжатию струи.
При истечении через цилиндрический насадок под уровень первый режим истечения не будет отличаться от описанного выше. Но при Н > Нкр перехода ко второму режиму не происходит, а начинается кавитационный режим.
Таким образом, внешний цилиндрический насадок имеет существенные недостатки: на первом режиме – большое сопротивление и недостаточно высокий коэффициент расхода, а на втором – очень низкий коэффициент расхода. Недостатком также является возможность кавитации при истечении под уровень.
Внешний цилиндрический насадок может быть значительно улучшен путем закругления входной кромки или устройства конического входа. На рис.5.9 даны различные типы насадков и указаны значения соответствующих коэффициентов.
Рис. 5.9. Истечение жидкости через насадки а – расширяющиеся конические; б – сужающиеся конические; в – коноидальные; г – внутренние цилиндрические
Конически сходящиеся и коноидальные насадки применяют там, где необходимо получить хорошую компактную струю сравнительно большой длины при малых потерях энергии (в напорных брандспойтах, гидромониторах и т.д.). Конически сходящиеся насадки используют для увеличения расхода истечения при малых выходных скоростях.
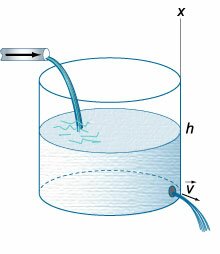
Рассмотрим случай опорожнения открытого в атмосферу сосуда при постоянно уменьшающемся напоре, при котором течение является неустановившемся (рис.5.10).
Однако если напор, а следовательно, и скорость истечения изменяются медленно, то движение в каждый момент времени можно рассматривать как установившееся, и для решения задачи применить уравнение Бернулли.
Рис. 5.10. Схема опорожнения резервуара
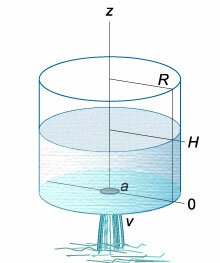
Обозначим переменную высоту уровня жидкости в сосуде за h, площадь сечения резервуара на этом уровнеS, площадь отверстия Sо, и взяв бесконечно малый отрезок времени dt, можно записать следующее уравнение объемов:
где dh – изменение уровня жидкости за время dt.
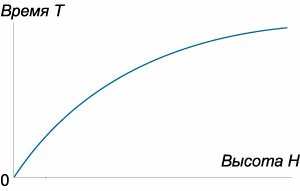
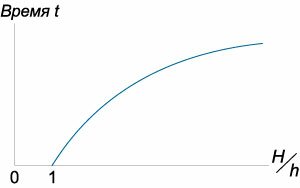
Отсюда время полного опорожнения сосуда высотой Н
Если будет известен закон изменения площади S по высоте h, то интеграл можно подсчитать. Для призматического сосуда S = const (рис.5.11), следовательно, время его полного опорожнения
Из этого выражения следует, что время полного опорожнения призматического сосуда в два раза больше времени истечения того же объема жидкости при постоянном напоре, равном первоначальному.
Для определения времени истечения жидкости из горизонтального цилиндрического сосуда (цистерны) (рис. 5.12) выразим зависимость переменной площади S от h:
где l – длина цистерны; D – диаметр цистерны.
Тогда время полного опорожнения такой цистерны, т.е. время изменения напора от h1 = D до h2 = 0, получится равным
Во многих водозаборных и водопропускных гидротехнических сооружениях расходы воды проходят через отверстия, перекрываемые затворами. Затворы поднимают на определенную высоту над дном и пропускают через отверстия необходимые расходы. Чаще всего на гидромелиоративных сооружениях устраивают отверстия прямоугольного сечения, истечение из которых и рассмотрим.
Отверстия могут быть незатопленными (истечение свободное) и затопленными, когда уровень воды за затвором влияет на истечение.
Если отверстие незатопленное, то вытекающая из-под затвора струя находится под атмосферным давлением (рис. 5.13). При истечении через затопленное отверстие струя за затвором находится под некоторым слоем воды (рис. 5.14).
Рис. 5.13. Истечение из-под затвора через незатопленное отверстие
Когда затвор приподнят над дном, вытекающая из-под него струя испытывает сжатие в вертикальной плоскости. На расстоянии, примерно равном высоте отверстия а (высоте поднятия затвора), наблюдается наиболее сжатое сечение. Глубина в сжатом сечении hc связана с высотой отверстия а следующей зависимостью:
hc = ε’a
где ε’ – коэффициент вертикального сжатия струи.
Коэффициент вертикального сжатия ε’ зависит от отношения высоты отверстия а к напору (глубине воды перед затвором) Н. Для ориентировочных расчетов можно принимать ε’ = 0,64.
Если составить уравнение Бернулли для сечений, проведенных перед затвором и в сжатом сечении, после преобразований получим:
где φ – коэффициент скорости,
где Н0 – напор с учетом скорости подхода,
Тогда расход при истечении из-под затвора при незатопленном отверстии определится по формуле:
где S – площадь отверстия, S = ab.
Рис. 5.14. Истечение из-под затвора при затопленном отверстии
При истечении через затопленное отверстие (рис. 5.14) расход определится по формуле:
где hz – глубина в том сечении, где наблюдается максимальное сжатие истекающей из-под затвора струи.
Глубина hz определяется из зависимости
в которой
а hб – глубина в отводящем канале (бытовая глубина).
Если вытекающая из отверстия или насадка струя попадает на неподвижную стенку, то она с определенным давлением воздействует на нее. Основное уравнение, по которому вычисляется давление струи на площадку, имеет вид
На рис. 5.15 приведены наиболее часто встречающиеся в практике ограждающие поверхности (преграды) и уравнения, по которым вычисляется давление струи на соответствующую поверхность.
Величина давления струи, естественно, зависит от расстояния насадка до преграды. С увеличением расстояния струя рассеивается и давление уменьшается. Соответствующие исследования показывают, что в данном случае струя может быть разбита на три характерные части: компактную, раздробленную и распыленную (рис.5.16).
В пределах компактной части сохраняется цилиндрическая форма струи без нарушения сплошности движения. В пределах раздробленной части сплошность потока нарушается, причем струя постепенно расширяется. Наконец, в пределах распыленной части струи происходит окончательный распад потока на отдельные капли.
Рис. 5.15. Взаимодействие струи жидкости с неподвижной поверхностью
Рис. 5.16. Составные части свободной струи
Источник
Истечение жидкости из отверстий и насадков
Подробности Категория: Гидравлика
Документальные учебные фильмы. Серия «Физика».
Истечение – если две материальные среды отделены друг от друга стенкой, имеющей отверстия, и давления, под которыми находятся эти среды, неодинаковы, то среда, находящаяся под большим давлением, исходит в соседнюю среду в виде струи – потока первой среды, ограниченного со всех сторон второй средой. Это явление называется истечением. И. происходит или под влиянием внешних сил, или под влиянием силы тяжести, или, наконец, под совокупным их действием. От И. нужно отличать выход одной среды в другую, находящуюся под тем же давлением, под влиянием одних внутренних (молекулярных сил); это явление есть диффузия (см.). И. тел наблюдается при всех трех состояниях их – твердом, жидком и газообразном. Легче и чаще всего наблюдается И. жидкостей, и поэтому И. изучено почти исключительно на жидкостях; найденные законы с успехом применены были впоследствии к твердым телам и газам. Теория И. составляет одну из важных глав гидродинамики – учения о движении жидкостей; практическая ее сторона и приложения рассматриваются в гидравлике или гидротехнике.
И. жидкостей.
Предполагая жидкость несжимаемой и не имеющей внутреннего трения, СПб. академик Д. Бернулли (1726) дал следующий основной закон для струй: если назовем скорость струи в одном ее сечении , давление в ней в этом месте , те же величины для другого сечения и , разницу по высоте этих двух сечений , ускорение силы тяжести – , a плотность жидкости , то
| . | (1.) |
Прилагая это уравнение к И. жидкости из отверстия в весьма тонкой стенке и полагая, что один конец струи есть внешняя поверхность жидкости с сечением , а другой – отверстие с сечением , и заметив, что для неразрывности струи необходимо, чтобы , находим общее выражение для скорости И.
| . | (2.) |
Если положим, что сечение отверстия совершенно незначительно в сравнении с сечением внешней поверхности, давления и одинаковы и И. жидкости происходит под влиянием одной силы тяжести, то получим
основной простой закон И. жидкостей под влиянием силы тяжести, опытно найденный (1643) Торричелли и опубликованный им в его сочинении «De Motu gravium projectorum». Этот закон, которым обыкновенно и пользуются в практической гидравлике, гласит, что скорость И. пропорциональна корню квадратному из высоты уровня жидкости над отверстием и из ускорения силы тяжести. Справедливость этого закона многократно проверялась от времен Торричелли до нашего времени на опытах различных исследователей (Гуглиельмини – XVII ст., Л. Вебер – 1879 г., Вотье – 1888 г. и др.) и найдена справедливой до % (Вотье). Из формулы (3) видно, что если в двух случаях И. высоты уровней относятся как 1:4, то соответственные скорости И. будут относиться, как 1:2, и что отношение скоростей И. на экваторе и полюсе будет относиться, как , т. е. как . Замечательно, что той же формулой (3) выражается скорость тела, упавшего с высоты , или скорость, которую следует придать телу, чтобы оно с земли поднялось вверх на высоту . Если отверстие в дне сосуда, то жидкость, как брошенное из отверстия тело, падает вертикальной струей вниз. Если же отверстие находится в боковом придатке сосуда и обращено кверху, то жидкость поднимается фонтаном вверх, до высоты уровня жидкости (см. Фонтан); в действительности вследствие трения воздуха и давления падающей уже вниз жидкости на подымающуюся струю и др. причин (см. ниже) высота фонтана никогда не достигает высоты уровня, а меньше ее; по Мариотту (1686), для достижения высоты фонтана в париж. фт. нужна разность уровней не в фт., но в ; позже Вейсбах дал более близкие к истине формулы для высоты фонтанов. Если отверстие сделано сбоку сосуда, то жидкость, следуя совокупному действию силы, выжимающей ее в горизонтальном направлении из отверстия, и силе тяжести, влекущей ее вертикально вниз, падает на землю струей, имеющей форму параболы, подобно тому, как падает брошенный горизонтально с той же скоростью камень. Из свойств параболы и формулы (3) выводим:
- расстояния точек падения струи от основания сосуда относятся, как корни квадратные из высот уровня над отверстием;
- расстояния точек падения пропорциональны корням квадратным из высот отверстия над поверхностями, на которые струи падают;
- две струи, из которых одна на столько же ниже уровня жидкости, на сколько другая выше поверхности падения, попадают на этой поверхности в точки, равноотстоящие от основания сосуда.
В закон Торричелли не входят величины, характеризующие жидкость, следовательно, скорость И. всех жидкостей одинакова; не нужно забывать, что это справедливо лишь для равных высот уровня, но не для равных давлений на жидкость – при равных давлениях скорости И. разных жидкостей обратно пропорциональны корням квадратным из их плотностей; так, напр., из парового котла с общим для воды и пара давлением в 8 атм. пар вытекает в 15 раз быстрее воды (Рэнкин). Небольшую разницу в скорости И. разных жидкостей производит их внутреннее трение (см. ниже). Если И. жидкости происходит из нескольких боковых отверстий, находящихся одно над другим, то законы И. весьма усложняются; скорость И. из какого-либо отверстия в этом случае менее той скорости, которая была бы, если над ним не было бы других отверстий.
До сих пор все относилось к тому случаю И., когда уровень во все время И. поддерживается постоянным; если же уровень не поддерживается постоянным, то он по мере И. падает все медленнее и медленнее ввиду все большего и большего уменьшения высоты уровня, и, наконец, И. прекращается, когда жидкость достигнет уровня отверстия. В гидравлике доказывается, что время, потребное на такое опорожнение сосуда, в два раза больше, чем время, в которое при неизменном первоначальном уровне выльется одинаковый объем жидкости. Для устройства водяных и песочных часов важно придать сосуду такую форму, чтобы во все время И. уровень в каждую единицу времени опускался на одну и ту же величину; теория дает для такого сосуда форму, похожую на форму цветка тюльпана, и приблизительно в такой форме и устраиваются эти часы. Если сосуд, из которого происходит И., сверху закрыть, то по мере И. воздух над жидкостью разрежается, давление на жидкость уменьшается, скорость И. замедляется и И. может даже совершенно приостановиться; случай этот исследован был Шевеном (1882). – Если отверстия значительны по размерам сравнительно с высотой уровня, то каждая часть струи имеет свою скорость и за среднюю скорость принимают обыкновенно скорость той частицы, которая проходит центр тяжести фигуры, представляющей отверстие. Результаты опытов показали, что все же в практике нельзя принимать скорость И., даваемую формулой Торричелли, за истинную, которая всегда меньше теоретической. В гидравлике формулу (3) пишут в следующем виде:
| . | (4.) |
где , по опытам разных наблюдателей, колеблется между 0,95 и единицей, в среднем = 0,97; причина этого отступления лежит, вероятно, в трении воды о стенки сосуда; вопрос об истинной величине его и даже вопрос о существовании его еще нельзя считать разрешенным.
Если вычислить количество вытекшей в единицу времени жидкости, взяв произведение сечения отверстия на скорость струи, то мы найдем, что вычисленное таким образом количество жидкости будет много больше истинного. Причину этого легко найти, если обратить внимание на то, что струя по выходе из отверстия конически суживается до некоторой толщины и затем продолжает течь с этим новым меньшим сечением струи. Причина этого сжатия струи (contractio venae) лежит в том, что частицы жидкости притекают к отверстию не только сверху, но и сбоку, а следовательно, имеют боковые скорости, благодаря которым идут наклонно к отверстию и сжимают струю. Явление это в первый раз замечено было Ис. Ньютоном и описано в его «Principia» (1714). При И. жидкости за размер отверстия И. следует принимать сечение наиболее узкой части струи, а следовательно, помножить истинное отверстие на отношение сечения его к сечению суженной струи; это отношение называется коэффициентом сжатия (контракции) – К. Формула для количества вытекшей жидкости:
| . | (5.) |
Средняя величина ; в действительности зависит от формы отверстия, от давления и множества других причин. Были попытки теоретически вычислить ; Бернулли дал , Байер (1848) – [ – отношение окружности к диаметру = 3,14159.], Рэлей (1879) и Кетер (1887) для отверстий в виде щели ; границы, теоретически возможные для для круглых отверстий в тонкой стенке, по Кетеру (1887),…. и . Опытно определяли величину Понселе, Пуазейль, Унвин, Вейсбах и др.; с увеличением отверстия и увеличением давления – уменьшается, хотя для некоторых форм отверстия изменения величины K следуют другим законам. – До сих пор мы рассматривали И. из весьма тонкой стенки; если стенка толста или отверстие имеет короткие насадки, то законы И. изменяются. Если насадка в виде короткой цилиндрической трубки входит внутрь жидкости (насадка Борда), то теория дает для K наименьшую величину , а опыты от 0,51 (Борда) до 0,55 (Бидоне). Если эта насадка представляет выходящий из стенок сосуда цилиндр, то сузившаяся струя снова расширяется и при выходе из насадки занимает уже все ее сечение; в этом случае, как дает теория и подтверждает опыт, . Если внешняя насадка имеет коническую форму, близкую к форме основания струи, то должно быть близко к 1, т. е. количество жидкости вытекшей должно быть близко к теоретическому; это и подтверждается опытом; так, Мишелотти нашел в этом случае . Сечение такой совершенной насадки легко построить, если нарисовать трапецию, большее основание которой равнялось бы диаметру отверстия , высота , нижнее основание , и бока которой заменены дугами радиуса . В случае такой насадки струя не представляет сужения и вполне примыкает к стенкам. Некоторыми комбинациями конических насадок можно даже сделать и почти равным .
В практической гидравлике (устройство плотин, шлюзов и т. д.) важен случай И. при посредстве перелива, т. е. когда одна из стенок сосуда имеет отверстие, доходящее до самого верха стенки, или когда вся стенка или часть ее ниже уровня жидкости. В этом случае теория дает для количества вытекшей в единицу времени жидкости
| , | (6.) |
где – глубина выреза в стенке, – длина его, а – толщина струи; величина , по наблюдениям Понселе и Лебро (1851), около , а коэффициент для этих случаев равен около 0,62. При этих данных формула (6) приобретает вид:
| . | (7.) |
В практической гидравлике пользуются для случая перелива и другими формулами, выведенными эмпирически. На основании почти исключительно эмпирических данных построены правила И. и для других весьма разнообразных случаев гидротехники.
Трение о стенки сосуда, почти не влияющее на И. при отверстиях в самой стенке, становится заметным, когда место И. соединено с сосудом длинной трубкой. В этом случае скорость И. меньше и величина формулы (2) приобретает вид:
| , | (8.) |
где некоторая величина, зависящая от трения о стенки трубки, которая выражается:
| , | (9.) |
где – длина трубы, – периметр еe отверстия, – еe сечение, а – коэффициент трения, зависящий от жидкости и от стенок трубки; величина зависит от скорости и, по г. Смису (1884), выражается формулой:
| (10.) |
где – диаметр трубки. Подробности течения по трубкам – см. Течение.
При И. жидкостей, смачивающих стенки трубок из самых тонких волосных (капиллярных) трубочек, главную роль играет уже не трение жидкости о стенки, а внутреннее собственное трение одних слоев жидкости о другие. Теорию этого случая И. дал Пуазейль (1842) и разработали Нейман, Гельмгольц и др. Для случая жидкости, смачивающей стенки сосуда, эти ученые вывели, что количество () вытекшей в единицу времени жидкости равно
| , | (11.) |
где – давление, – радиус трубки, – ее длина, – коэффициент внутреннего трения, а . Пользуясь этой формулой, выводят обыкновенно коэффициенты внутреннего трения на основании наблюдений над И. жидкостей из волосных трубок.
По материалам Викитека
Источник