Вывести формулу для расчета давления жидкости на дно сосуда

1. Вывод формулы для давления жидкости на дно сосуда

Для того чтобы упростить вывод формулы для расчета давления на дно и стенки сосуда, удобнее всего использовать сосуд в форме прямоугольного параллелепипеда (Рис. 1).

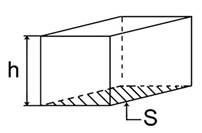
Сосуд для расчета давления жидкости

Рис. 1. Сосуд для расчета давления жидкости

Площадь дна этого сосуда – S, его высота – h. Предположим, что сосуд наполнен жидкостью на всю высоту h. Чтобы определить давление на дно, нужно силу, действующую на дно, разделить на площадь дна. В нашем случае сила – это вес жидкости P, находящейся в сосуде

Поскольку жидкость в сосуде неподвижна, ее вес равен силе тяжести, которую можно вычислить, если известна масса жидкости m

Напомним, что символом g обозначено ускорение свободного падения.

Для того чтобы найти массу жидкости, необходимо знать ее плотность ρ и объем V

Объем жидкости в сосуде мы получим, умножив площадь дна на высоту сосуда

Эти величины изначально известны. Если их по очереди подставить в приведенные выше формулы, то для вычисления давления получим следующее выражение:

В этом выражении числитель и знаменатель содержат одну и ту же величину S – площадь дна сосуда. Если на нее сократить, получится искомая формула для расчета давления жидкости на дно сосуда:

Итак, для нахождения давления необходимо умножить плотность жидкости на величину ускорения свободного падения и высоту столба жидкости.

2. Давление жидкости на стенки сосуда

Полученная выше формула называется формулой гидростатического давления. Она позволяет найти давление на дно сосуда. А как рассчитать давление на боковые стенки сосуда? Чтобы ответить на этот вопрос, вспомним, что на прошлом уроке мы установили, что давление на одном и том же уровне одинаково во всех направлениях. Это значит, давление в любой точке жидкости на заданной глубине h может быть найдено по той же формуле.

3. Анализ и примеры применения полученной формулы

Рассмотрим несколько примеров.

Возьмем два сосуда. В одном из них находится вода, а в другом – подсолнечное масло. Уровень жидкости в обоих сосудах одинаков. Одинаковым ли будет давление этих жидкостей на дно сосудов? Безусловно, нет. В формулу для расчета гидростатического давления входит плотность жидкости. Поскольку плотность подсолнечного масла меньше, чем плотность воды, а высота столба жидкостей одинакова, то масло будет оказывать на дно меньшее давление, чем вода (Рис. 2).

Жидкости с различной плотностью при одной высоте столба оказывают на дно различные давления

Рис. 2. Жидкости с различной плотностью при одной высоте столба оказывают на дно различные давления

Еще один пример. Имеются три различных по форме сосуда. В них до одного уровня налита одна и та же жидкость.

Будет ли одинаковым давление на дно сосудов? Ведь масса, а значит, и вес жидкостей в сосудах различен. Да, давление будет одинаковым (Рис. 3). Ведь в формуле гидростатического давления нет никакого упоминания о форме сосуда, площади его дна и весе налитой в него жидкости. Давление определяется исключительно плотностью жидкости и высотой ее столба.

Давление жидкости не зависит от формы сосуда

Рис. 3. Давление жидкости не зависит от формы сосуда

4. Заключение

Мы получили формулу для нахождения давления жидкости на дно и стенки сосуда. Этой формулой можно пользоваться и для расчета давления в объеме жидкости на заданной глубине. Она может быть использована для определения глубины погружения аквалангиста, при расчете конструкции батискафов, подводных лодок, для решения множества других научных и инженерных задач.

Источник

«Кто смолоду больше делает и думает сам, тот становится потом надежнее, крепче, умнее». С. Нерис

Цели урока:

Образовательные:
1. активизировать знания учащихся о причинах возникновения давления жидкости,
2. создать условия для овладения учащимися формулы для расчета давления жидкости на дно и стенки сосуда,
3. продолжить работу по формированию навыков научного познания мира,
4. создать условия для овладения учащимися эвристическим методом представления наблюдаемого явления – методом графических образов.
Развивающие:
1. развивать экспериментальные умения, навыки логического мышления, умение обосновывать свои высказывания, делать выводы, выделять главное, представлять информацию в различных знаковых системах,
2. развивать у учащихся интерес к познанию законов природы и их применению;
3. развивать умение проводить рефлексию своей деятельности.
Воспитательные:
1. создать условия для приобретения убежденности учащихся в познаваемости окружающего мира,
2. приучать учащихся к доброжелательному общению, взаимопомощи, к самооценке.

Читайте также: Сосуды от дуги аорты

Задачи урока:

изучение теоретического материала;
решение задач на расчет давления в жидкости и газе;
практическое значение знаний о давлении жидкости.

План урока:

Организационный момент. (1 мин.)
Актуализация знаний. (5 мин.)
Объяснение материала. (20 мин.)
Закрепление материала. (15 мин.)
Рефлексия. (2 мин.)
Домашнее задание. (2 мин.)

Ход урока

I. Организационный момент.

(На партах учащихся лежат рабочие карты урока, в которых представлены две самостоятельные работы и критерии выставления оценки; две ручки с разными стержнями, например синий и зеленый; таблицы плотностей веществ, учебники и тетради).

II. Актуализация знаний.

Самостоятельная работа (см. рабочую карту)

III. Объяснение нового материала

Провожу эксперимент: в пластмассовую бутылку с тремя отверстиями на разных уровнях по высоте наливаем подкрашенную воду.

Беседа с классом:

почему вода вытекает из сосуда?
сравните струи воды?
объясните, почему они разные?

Когда учащиеся объяснят, что столбы жидкости разные и давление на разной глубине разное, ставлю проблему: а нужно ли знать людям, чему равно давление жидкости на разных глубинах, на дно, на стенки сосуда?

Открываем тетради, записываем тему урока.

Ставим цель: вывести формулу для расчета давления жидкости на дно и стенки сосуда.

Давление жидкости (см. презентация)

Вокруг нас много жидкостей. Одни из них движутся, например, вода в реках или нефть в трубах, другие – покоятся. При этом все они имеют вес и поэтому давят на дно и стенки сосуда, в котором находятся. Подсчет давления движущейся жидкости – непростая задача, поэтому изучим лишь как рассчитывать давление, создаваемое весом покоящейся жидкости. Оно называется гидростатическим давлением и вычисляется по следующей формуле.


	p – давление слоя жидкости, Па
	ρ – плотность жидкости, кг/м3
	g – коэффициент, Н/кг
	h – высота слоя жидкости, м

Рассмотрим, как выведена эта формула. Сила F, с которой жидкость давит на дно сосуда, является весом жидкости. Его мы можем подсчитать по формуле F тяж = mg, так как жидкость и ее опора (дно сосуда) покоятся. Вспомним также формулу m = ρV для выражения массы тела через плотность его вещества и формулу V = Sh для подсчета объема тела, имеющего форму прямоугольного параллелепипеда. В результате имеем равенство:

Это равенство иллюстрирует не только способ вывода формулы для вычисления гидростатического давления. Оно также показывает, что формула p = ρgh является частным случаем определения давления – формулы p = F/S.

Заметим также, что при выводе формулы совсем необязательно предполагать, что слой высотой h и плотностью ρ образован именно жидкостью. В наших рассуждениях ничего не изменится, если вместо давления жидкости мы рассмотрим давление твердого тела прямоугольной формы или даже газа, заключенного в соответствующий сосуд. Создаваемое ими весовое давление будет именно таким, как предсказывает формула p = ρgh.

Формула p = ρgh показывает, что давление, создаваемое слоем жидкости, не зависит от ее массы, а зависит от плотности жидкости, высоты ее слоя и места наблюдения. При увеличении толщины слоя жидкости или ее плотности гидростатическое давление будет возрастать.

Полученный нами вывод можно проверить опытами. Проделаем их. Справа изображена стеклянная трубка с водой, дно которой затянуто тонкой резиновой пленкой. Увеличивая высоту слоя налитой жидкости, мы будем наблюдать увеличение растяжения пленки. Этот опыт подтверждает, что при увеличении высоты слоя жидкости создаваемое ею давление увеличивается.

На следующем рисунке изображены трубки с водой и “крепким” раствором соли. Видно, что уровни жидкостей находятся на одной и той же высоте, но давление на пленку в правой трубке больше. Это объясняется тем, что плотность раствора соли больше, чем плотность обычной воды.

На доске нарисован параллелепипед высотой h и площадью основания S. Предлагаю ребятам представить, что это аквариум, в котором налита вода. Попытаемся определять давление воды Р на дно аквариума. Работаем на магнитной доске с карточками, выкладывая поочередно формулы, получая цепочку: m=ρV, V=Sh, m=ρSh, P=gm, P=gρSh, ρ=P/S, p=ρgh.

Анализируем окончательную формулу: что же нужно знать, чтобы рассчитать давление жидкости.

Зависит ли давление от площади или формы сосуда?

Вьполняем фронтальный эксперимент: на каждой парте стоит стакан с водой. Высота налитой воды одинаковая.

Цель: определить давление воды на дно стакана.

Один ученик выполняет у доски. Остальные за партой. Сверяем ответ. Анализируем его: какую физическую величину мы измеряли? какую физическую величину брали в таблице? какое численное значение давления получили учащиеся, работающие за партой и у доски? большое это или маленькое давление?

IV. Закрепление изученного материала.

~ Приведи примеры движущихся жидкостей.
И движущиеся, и покоящиеся жидкости оказывают давление …
Гидростатическое давление – это …
~ Произведение в правой части формулы для вычисления гидростатического давления представляет собой …
~ По какой формуле мы сможем подсчитать вес покоящейся жидкости?
Объем слоя жидкости мы нашли при помощи произведения …
Выражение “p = … = ρgh” представляет собой …
~ О чем говорит равенство p=ρgh?
Как можно подтвердить справедливость формулы p=ρgh?
~ Увеличение растяжения пленки свидетельствует, что …
Описанный опыт иллюстрирует зависимость гидростатического давления от ..
~ Плотность раствора соли больше, чем плотность воды. Это приводит к тому, что …
Этот опыт иллюстрирует зависимость давления жидкости от ее плотности. Эта иллюстрация стала возможной благодаря тому, что …

Расчетные задачи

а) Высота столба воды в стакане 8 см. Какое давление на дно стакана оказывает вода? Какое давление оказывала бы ртуть, если бы она была налита вместо воды?
б) Какое давление на дно сосуда оказывает слой керосина высотой 1,5 м?

Качественные задачи

в) Волк плывет под водой с дыхательной трубкой. Какие ограничения накладывает на ныряльщика дыхательная трубка? Ответ найдите в учебнике стр. 95.

Задача с недостающими данными

г) Какое давление на глубине 1,5 м? Решить устно.

Качественные задачи, предполагающие работу с дополнительными источниками информации

д) Какое преимущество дает ныряльщику акваланг? Какие ограничения он накладывает? Ответ в учебнике.

е) В следующем сюжете мы видим глубоководный аппарат. Почему у него такая внешняя форма?

ж) Чтобы человек мог работать на больших глубинах он должен находиться в специальном скафандре. Найдите о нем информацию в учебнике.

з) Анализируя рис. 103 учебника давайте познакомимся с тем, что говорит нам учебник о глубоководных аппаратах. Какие ограничения в их использовании имеются?

и) Вычислите, какое давление в самой глубокой Мариинской впадине глубиной.
к) В просмотренном сюжете мы видели с вами глубоководных рыб. Какую длину лески нужно приготовить для лова рыбы камбалы, если она может выдерживать давление 400 кПа.

V. Задаю домашнее задание:

параграф из учебника, упражнение на решение задач и сообщения:

«Человек изучает подводный мир».
«Подводные лодки, батисферы и батискафы».
«Животный мир океанских и морских глубин».
«Ныряльщики за жемчугом».

Источник

Что такое давление жидкости

Наука гидростатика исследует ситуации, когда движение в жидкости отсутствует или скорость пренебрежимо мала, и позволяет понять некоторые свойства такой важной гидродинамической величины, как давление.

Теорема

Давление — физическая величина, описывающая силу, которая действует перпендикулярно поверхности на единицу ее площади. Для ее обозначения используется символ р или Р.

На опору под действием силы тяжести давят и твердые, и сыпучие вещества, но их воздействие отличается от гидростатического давления. Воздействие твердого тела определяется его весом, жидкости — ее глубиной. В газе и жидкости давящее воздействие на поверхности создается за счет хаотических столкновений молекул и связано с другими параметрами состояния вещества — например, температурой Т и плотностью (rho.)

Для жидкости, учитывая ее малую сжимаемость, вместо уравнения Клапейрона, учитывающего температуру и молярную массу газа, обычно используют условие несжимаемости, которое существенно упрощает уравнения гидроаэромеханики:

(rho = const.)

Сила гидростатического давления р на дно сосуда не зависит от его формы и изменяется пропорционально уровню налитой в сосуд жидкости и ее плотности в соответствии с основной гидростатической формулой:

(р = р_{0} + rhotimes gtimes h.)

(rho) здесь — плотность вещества, (р_{0}) — атмосферное давление, g — ускорение свободного падения, h — глубина погружения.

История открытия

Гидростатика как наука была достаточно хорошо известна еще в античные времена, поскольку она тесно связана с практической деятельностью людей. Для строительства лодок и кораблей, колодцев и различных гидравлических аппаратов, например, поршневых насосов, необходимо было понимать, как вода взаимодействует с твердыми материальными предметами.

Различие между давлением твердого тела и воды очень эффектно пояснил на опыте Блез Паскаль: всего лишь стакан воды, вылитый в высокую тонкую трубку, соединенную с наполненной водой закрытой бочкой, создал такое избыточное давление, что вода через щели брызнула наружу.

Определение

В 1653 году Паскаль сформулировал свой закон: давление, производимое на жидкость или газ, передается в любую точку одинаково.

Позже был сконструирован прибор, демонстрирующий действие закона Паскаля. Он называется шар Паскаля и представляет собой заполняемый водой шар с маленькими отверстиями, соединенный с цилиндрической рукояткой, внутри которой движется поршень. Внешнее давление, производимое поршнем, передается во все точки воды одинаково, и она выплескивается в виде одинаковых струек. Поэтому струйки, вытекающие из отверстий, расположенных в горизонтальной плоскости, оставляют на полу следы равной длины.

Факторы, влияющие на показатель

На давление жидкости могут влиять:

ее плотность;
атмосферное давление;
температура;
глубина сосуда;
площадь дна сосуда.

Давление на дно и стенку сосуда

Закон Паскаля утверждает, что давление в любом месте покоящейся жидкости или газа по всем направлениям одинаково, причем оно одинаково передается по всему объему вещества. Таким образом, разницы между давлением на дно и на стенку нет.

Расчет давления жидкости на дно и стенки сосуда

Чтобы найти давление на дно сосуда, нужно взять приведенное выше основное уравнение гидростатики и подставить туда глубину, плотность и атмосферное давление.

В случае стенок непосредственно прилагать эту формулу можно только к бесконечно малым горизонтальным полоскам на боковых стенках сосуда. Чтобы рассчитать давление на стенки, нужно суммировать давление на все горизонтальные элементы их поверхности, используя правила интегрального исчисления. Паскаль, проведя эти расчеты, доказал, что от формы сосуда давление жидкости не зависит.

Единицы измерения

В международной системе единиц давление измеряется в Паскалях. Один Паскаль равен силе в один ньютон, производящей равномерное давление на единицу поверхности в один метр. Но на практике часто используют такую единицу измерения, как атмосфера, равную 76 см ртутного столба при нулевой температуре по Цельсию.

Определение

Атмосфера — внесистемная единица измерения, которая примерно означает давление атмосферы Земли на уровне Мирового океана.

Формулы расчета

Для описания процессов в гидравлических прессах или любых других системах, в которых давление собственно жидкостей ничтожно мало по сравнению с передаваемым им извне, используется формула закона Паскаля:

(р = frac{F}{S}.)

F — сила, с которой происходит воздействие на поверхности сосуда, S — площадь этой поверхности.

В учебных задачах обычно опускают такой параметр, как атмосферное давление, и используют для расчетов формулу:

(р = rhotimes gtimes h.)

Можно вывести эту формулу для сосудов, имеющих форму прямой призмы или цилиндра, из закона Паскаля.

(m = rhotimes V = rhotimes Stimes h)

Вес (Р = g times m = gtimes rhotimes Stimes h.)

Вес столба, давящего на дно сосуда, равен силе, и тогда:

(р = frac{Р}{S} = gtimes rhotimes Stimes frac{h}{S} = gtimes rhotimes h.)

Применение на практике

Для гидравлических механизмов, например, прессов, можно рассчитать пропорциональный изменению площади выигрыш в силе, зная, во сколько раз увеличивается площадь большего поршня по сравнению с меньшим.

Соотношение между полезной и затраченной работой описывается понятием КПД, коэффициент полезного действия, и рассчитывается по формуле:

(frac{F_{2}h_{2}}{F_{1}h_{1}})

Также закон Паскаля описывает работу жидкостных манометров, приборов для измерения давления, отличного от атмосферного. Давление в одном колене манометра вызывает повышение жидкости в другом колене — это явление называется избыточным столбом. По его высоте, соотнося ее с нанесенной шкалой, пользователь прибора узнает точную цифру в миллиметрах ртутного столба.

Гидростатический парадокс

Согласно гидростатическому парадоксу, давление жидкости на любую плоскую стенку равняется весу столба этой жидкости, давящему на основание, площадь которого равна площади этой стенки. Поэтому от формы емкости давление не зависит. Если емкость расширяется к горлышку, то вес содержимого распределяется по наклонным стенкам и передается вниз через стенки, не давя на дно, а если емкость к горлышку сужается, то содержимое давит на стенки снизу вверх, что уменьшает его воздействие на дно.

Источник