Вывод о расчете давления ее на дно сосуда
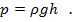
Что это такое?
В сосуде, заполненном водой, на дно давит сила, равная весу столба жидкости. Это вызванное силой тяжести давление называется гидростатическим.
Оно определяется отношением силы к площади, то есть его физический смысл – это сила, действующая на единицу площади (см2).
 Законы гидростатики описал Блез Паскаль. В 1648 г. он удивил горожан опытом, демонстрирующим свойства воды.
Законы гидростатики описал Блез Паскаль. В 1648 г. он удивил горожан опытом, демонстрирующим свойства воды.
Вставив в бочку, заполненную водой, длинную узкую трубку, он налил в нее несколько кружек воды, и бочку разорвало.
Согласно закону Паскаля, приложенное к H2O усилие распространяется равномерно во всем объеме. Это объясняется тем, что вода почти не сжимается. В гидравлических прессах используют это свойство.
Плотность воды все же растет при высоком давлении. Это учитывается при расчетах конструкций глубоководных аппаратов.
Факторы, влияющие на показатель
При отсутствии внешнего воздействия, играют роль два фактора:
- высота столба;
- плотность.
Выше уровень воды, налитой в сосуд, — выше напор на дно. Если в одной емкости ртуть, а в другой вода и при этом уровни жидкостей одинаковы, то в первом случае давление на дно больше, так как ртуть имеет большую плотность.
Сверху на содержимое сосуда давит также атмосферный воздух. Поэтому в сообщающихся сосудах уровень одинаков, ведь в каждом из них над поверхностью атмосфера одна и та же.
Если же к поверхности приложить поршень и давить на него, то напор будет складываться из:
- внешней силы;
- веса воды.
При этом форма сосуда не определяет размер усилия, создаваемого столбом. Оно будет одним и тем же при равной высоте столба, хотя стенки емкости могут расширяться кверху или сужаться.

На дно и стенку сосуда – в чем разница?
Вода, заполняющая емкость, оказывает давление по направлению всегда перпендикулярно поверхности твердого тела, по всей площади соприкосновения с дном и стенками.
Усилие на дно распределено равномерно, то есть оно одинаково в любой точке. Заполнив водой сито, можно увидеть, что струи, текущие через отверстия, равны по напору.
Наполнив сосуд, имеющий отверстия одного диаметра в стенках на разной высоте, можно наблюдать различный напор вытекающей струи. Чем выше отверстие – тем слабее струя. То есть, давление на стенки емкости тем больше, чем ближе ко дну.
Единицы измерения
 Давление воды измеряют в:
Давление воды измеряют в:
- паскалях – Па;
- метрах водяного столба – м. в. ст.
- атмосферах – атм.
Практически достаточно знать, что 1 атмосфера равна 10 метрам водяного столба или 100000 Па (100кПа).
Формулы расчета
Давление на дно сосуда рассчитывается делением силы на площадь, то есть оно равно произведению плотности воды, высоты столба и ускорения свободного падения g (величина постоянная, равна 9,8 м/с2).
Пример расчета: бак наполнен водой (плотность 1000 кг/м3) до высоты 1,2 м. Нужно найти, какое давление испытывает дно бака. Решение: P = 1000*1, 2*9, 8 = 11760 Па, или 11, 76 кПа.
Для расчета давления на стенки сосуда применяют все ту же формулу напора, приведенную выше. При расчете берется глубина от точки, в которой нужно рассчитать напор, до поверхности воды.
Пример расчета: на глубине 5 м на стенку резервуара с водой будет оказываться давление P=1000 *5 * 9, 8=49000 кПа, что составляет 0,5 атмосферы.
Расчет давления воды на дно и стенки сосуда в видео:
Применение на практике
Примеры использования знаний свойств воды:
-
 Подбирая насос для водоснабжения дома высотой 10 м, понимают, что напор должен быть минимум 1 атм.
Подбирая насос для водоснабжения дома высотой 10 м, понимают, что напор должен быть минимум 1 атм. - Водонапорная башня снабжает водой дома ниже ее по высоте, напор в кране у потребителей обеспечен весом столба воды в баке.
- Если в стенках бочки появились отверстия, то, чем ниже они расположены, тем более прочным должен быть материал для их заделки.
- Замеряют дома напор холодной воды в кране манометром. Если он менее чем 0,3 атм (установлено санитарными нормами), есть основания для претензий к коммунальщикам.
Используя гидравлический пресс, можно получить большое усилие, при этом приложив малую силу. Примеры применения:
- выжимка масла из семян растений;
- спуск на воду со стапелей построенного судна;
- ковка и штамповка деталей;
- домкраты для подъема грузов.
Заключение
Такие свойства воды, как текучесть и несжимаемость, дают возможность использовать силу ее давления для самых различных целей.
Опасность этого явления учитывают при расчетах на прочность корпусов подводных лодок, стенок и днищ резервуаров, в которых хранят воду. Сила давления воды совершает полезную работу, она же способна и разрушать.
А какова Ваша оценка данной статье?
Источник
1. Вывод формулы для давления жидкости на дно сосуда
Для того чтобы упростить вывод формулы для расчета давления на дно и стенки сосуда, удобнее всего использовать сосуд в форме прямоугольного параллелепипеда (Рис. 1).
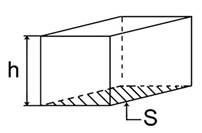
Рис. 1. Сосуд для расчета давления жидкости
Площадь дна этого сосуда – S, его высота – h. Предположим, что сосуд наполнен жидкостью на всю высоту h. Чтобы определить давление на дно, нужно силу, действующую на дно, разделить на площадь дна. В нашем случае сила – это вес жидкости P, находящейся в сосуде
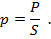
Поскольку жидкость в сосуде неподвижна, ее вес равен силе тяжести, которую можно вычислить, если известна масса жидкости m
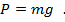
Напомним, что символом g обозначено ускорение свободного падения.
Для того чтобы найти массу жидкости, необходимо знать ее плотность ρ и объем V
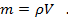
Объем жидкости в сосуде мы получим, умножив площадь дна на высоту сосуда
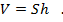
Эти величины изначально известны. Если их по очереди подставить в приведенные выше формулы, то для вычисления давления получим следующее выражение:
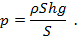
В этом выражении числитель и знаменатель содержат одну и ту же величину S – площадь дна сосуда. Если на нее сократить, получится искомая формула для расчета давления жидкости на дно сосуда:
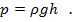
Итак, для нахождения давления необходимо умножить плотность жидкости на величину ускорения свободного падения и высоту столба жидкости.
2. Давление жидкости на стенки сосуда
Полученная выше формула называется формулой гидростатического давления. Она позволяет найти давление на дно сосуда. А как рассчитать давление на боковые стенки сосуда? Чтобы ответить на этот вопрос, вспомним, что на прошлом уроке мы установили, что давление на одном и том же уровне одинаково во всех направлениях. Это значит, давление в любой точке жидкости на заданной глубине h может быть найдено по той же формуле.
3. Анализ и примеры применения полученной формулы
Рассмотрим несколько примеров.
Возьмем два сосуда. В одном из них находится вода, а в другом – подсолнечное масло. Уровень жидкости в обоих сосудах одинаков. Одинаковым ли будет давление этих жидкостей на дно сосудов? Безусловно, нет. В формулу для расчета гидростатического давления входит плотность жидкости. Поскольку плотность подсолнечного масла меньше, чем плотность воды, а высота столба жидкостей одинакова, то масло будет оказывать на дно меньшее давление, чем вода (Рис. 2).

Рис. 2. Жидкости с различной плотностью при одной высоте столба оказывают на дно различные давления
Еще один пример. Имеются три различных по форме сосуда. В них до одного уровня налита одна и та же жидкость.
Будет ли одинаковым давление на дно сосудов? Ведь масса, а значит, и вес жидкостей в сосудах различен. Да, давление будет одинаковым (Рис. 3). Ведь в формуле гидростатического давления нет никакого упоминания о форме сосуда, площади его дна и весе налитой в него жидкости. Давление определяется исключительно плотностью жидкости и высотой ее столба.

Рис. 3. Давление жидкости не зависит от формы сосуда
4. Заключение
Мы получили формулу для нахождения давления жидкости на дно и стенки сосуда. Этой формулой можно пользоваться и для расчета давления в объеме жидкости на заданной глубине. Она может быть использована для определения глубины погружения аквалангиста, при расчете конструкции батискафов, подводных лодок, для решения множества других научных и инженерных задач.
Источник
Возьмем
цилиндрический сосуд с горизонтальным дном и вертикальными стенками,
наполненный жидкостью до высоты (рис. 248).
Рис. 248. В
сосуде с вертикальными стенками сила давления на дно равна весу всей налитой
жидкости
Рис. 249. Во
всех изображенных сосудах сила давления на дно одинакова. В первых двух сосудах
она больше веса налитой жидкости, в двух других — меньше
Гидростатическое
давление в каждой точке дна сосуда будет одно и то же:
.
Если
дно сосуда имеет площадь , то сила давления жидкости на дно
сосуда ,
т. е. равна весу жидкости, налитой в сосуд.
Рассмотрим
теперь сосуды, отличающиеся по форме, но с одинаковой площадью дна (рис. 249).
Если жидкость в каждом из них налита до одной и той же высоты , то давление на
дно . во
всех сосудах одно и то же. Следовательно, сила давления на дно, равная
,
также
одинакова во всех сосудах. Она равна весу столба жидкости с основанием, равным
площади дна сосуда, и высотой, равной высоте налитой жидкости. На рис. 249 этот
столб показан около каждого сосуда штриховыми линиями. Обратите внимание на то,
что сила давления на дно не зависит от формы сосуда и может быть как больше,
так и меньше веса налитой жидкости.
Рис. 250.
Прибор Паскаля с набором сосудов. Сечения одинаковы у всех сосудов
Рис. 251.
Опыт с бочкой Паскаля
Этот
вывод можно проверить на опыте при помощи прибора, предложенного Паскалем (рис.
250). На подставке можно закреплять сосуды различной формы, не имеющие дна.
Вместо дна снизу к сосуду плотно прижимается подвешенная к коромыслу весов
пластинка. При наличии жидкости в сосуде на пластинку действует сила давления,
которая отрывает пластинку, когда сила давления начнет превосходить вес гири,
стоящей на другой чашке весов.
У
сосуда с вертикальными стенками (цилиндрический сосуд) дно открывается, когда
вес налитой жидкости достигает веса гири. У сосудов другой формы дно
открывается при той же самой высоте столба жидкости, хотя вес налитой воды
может быть и больше (расширяющийся кверху сосуд), и меньше (суживающийся сосуд)
веса гири.
Этот
опыт приводит к мысли, что при надлежащей форме сосуда можно с помощью
небольшого количества воды получить огромные силы давления на дно. Паскаль
присоединил к плотно законопаченной бочке, налитой водой, длинную тонкую
вертикальную трубку (рис. 251). Когда трубку заполняют водой, сила
гидростатического давления на дно становится равной весу столба воды, площадь
основания которого равна площади дна бочки, а высота равна высоте трубки.
Соответственно увеличиваются и силы давления на стенки и верхнее днище бочки.
Когда Паскаль заполнил трубку до высоты в несколько метров, для чего потребовалось
лишь несколько кружек воды, возникшие силы давления разорвали бочку.
Как
объяснить, что сила давления на дно сосуда может быть, в зависимости от формы
сосуда, больше или меньше веса жидкости, содержащейся в сосуде? Ведь сила,
действующая со стороны сосуда на жидкость, должна уравновешивать вес жидкости.
Дело в том, что на жидкость в сосуде действует не только дно, но и стенки
сосуда. В расширяющемся кверху сосуде силы, с которыми стенки действуют на
жидкость, имеют составляющие, направленные вверх: таким образом, часть веса
жидкости уравновешивается силами давления стенок и только часть должна быть
уравновешена силами давления со стороны дна. Наоборот, в суживающемся кверху
сосуде дно действует на жидкость вверх, а стенки — вниз; поэтому сила давления
на дно оказывается больше веса жидкости. Сумма же сил, действующих на жидкость
со стороны дна сосуда и его стенок, всегда равна весу жидкости. Рис. 252
наглядно показывает распределение сил, действующих со стороны стенок на
жидкость в сосудах различной формы.
Рис. 252.
Силы, действующие на жидкость со стороны стенок в сосудах различной формы
Рис. 253. При
наливании воды в воронку цилиндр поднимается вверх.
В
суживающемся кверху сосуде со стороны жидкости на стенки действует сила,
направленная вверх. Если стенки такого сосуда сделать подвижными, то жидкость
поднимет их. Такой опыт можно произвести на следующем приборе: поршень
неподвижно закреплен, и на него надет цилиндр, переходящий в вертикальную
трубку (рис. 253). Когда пространство над поршнем заполняется водой, силы
давления на участках и стенок цилиндра поднимают цилиндр
вверх.
Источник
Тип урока: урок открытия и первичного закрепления знаний
Задачи: обеспечить усвоение знаний о давлении жидкости на дно и стенки сосуда; отработать навыки применения правила расчёта давления жидкости при решении задач
Планируемые результаты
Предметные: повторение темы «Гидростатическое давление. Закон Паскаля; формирование представлений о давлении жидкости на дно и стенки сосуда. Приобретение опыта применения научных методов познания для расчета давления жидкости на дно и стенки сосуда. o Проведение текущего контроля.
Метапредметные:
Познавательные – ставить и формировать новые задачи в учёбе;
Регулятивные – умение соотносить свои действия с планируемыми результатами;
Коммуникативные; планирование учебного сотрудничества со сверстниками, постановка вопросов — инициативное сотрудничество в поиске и сборе информации, умение полно и точно выражать свои мысли
Личностные: формирование ответственного отношения к учению, готовности и способности обучающихся к саморазвитию на основе мотивации к обучению и познанию мира; готовность к саморазвитию и самообразованию
Организационная структура
Этап урока
Содержание деятельности учителя
Содержание деятельности обучающегося
Формируемые способы деятельности
1
2
3
4
I.Организационный момент
Приветствие готовности учащихся к уроку. Создание в классе атмосферы психологического комфорта.
Готовятся к работе на уроке. Настраиваются на учебную деятельность.
Формировать навыки самоорганизации
1
2
3
4
II. Проверка домашнего задания
. 1. Как передают давление жидкости и газы?
2. Пользуясь рис.99, объясните, почему жидкости и газы передают давление во все стороны без изменений?
3. Сформулируйте закон Паскаля
4.Слайд 2. Учитель: Что показывает опыт?
5. Слайд 3. О чем свидетельствует данный опыт?
6. Слайд 4. А если пленка закрывает не дно, а боковое отверстие на трубке, что будет происходить с пленкой при опускании трубки в сосуд с жидкостью
7. Слайд5. Что показывают нам данный опыт?
8. Слайд 6. Учитель. Какой вывод можно сделать из данного опыта?
9. Слайд 7. Какие выводы мы можем сделать данных из опытов:
1. Ответ
2.Овет
3. Ответ
4.Чем выше столб воды над резиновой пленкой, тем больше она прогибается – тем больше оказываемое жидкостью давление.
5. . Наступает полное выпрямление пленки тогда, когда уровни воды в трубке и сосуде совпадают
6. Происходит выпрямление плёнки тогда, когда уровни воды в трубке и сосуде совпадают.
7. Силы, действующие на резиновую плёнку, одинаковы со всех сторон, значит давление на одном и том же уровне во всех направлениях одинаково.
8. Ученик. Внутри воды существует давление. При совпадении уровней воды в трубке и сосуде давления одинаковы по всем направлениям.
9. 1. Внутри жидкости существует давление.2 На одном и том же уровне давление одинаково по всем направлениям.3. С глубиной давление увеличивается.
Уметь оценивать достижения других учеников
Постановка проблемы
Эксперимент: в стеклянную трубку с тремя отверстиями на разных уровнях по высоте наливаем подкрашенную воду.
1.Сравните струи воды? Используя законы физики, объясните, почему они разные?
2. Нужно ли знать людям, чему равно давление жидкости на разных глубинах, на дно, на стенки сосуда?
1.Ответ: столбы жидкости разные и давление на разной глубине разное.)
2.Высказывают своё мнение и предположения.
Выражать свои мысли в соответствии с задачей.
III.Определить тему и цели урока
Ребята как выдумаете, о чем мы будем говорить сегодня на уроке?
Тема нашего урока «расчет давления на дно и стенки сосуда»
Чтобы вы хотели узнать по этой теме?
Как вы думаете, от чего может зависеть давление на дно и стенки сосуда?
Cегодня мы с вами установим от чего зависит давление на дно и стенки сосуд
Для того чтобы упростить вывод формулы для расчета давления на дно и стенки сосуда, удобнее всего использовать сосуд в форме прямоугольного параллелепипеда (Рис. 1).
Давайте выведем эту формулу вместе. Вызываю ученика к доске.
Слайд 9.10
Полученная выше формула называется формулой гидростатического давления. Она позволяет найти давление на дно сосуда. А как рассчитать давление на боковые стенки сосуда? Чтобы ответить на этот вопрос, вспомним, что на прошлом уроке мы установили, что давление на одном и том же уровне одинаково во всех направлениях.
Высказывают свои предположения.
от чего зависит давление и какая формула для вычисления давления
Высказывают свои предположения
Ученик с помощью класса и наводящих вопросов выводит формулу для нахождения давления на дно и стенки сосуда
Это значит, давление в любой точке жидкости на заданной глубине h может быть найдено по той же формуле.
Формировать умения принимать и сохранять учебную задачу
Слайды 11, 12 подтверждающие зависимость давления от высоты столба и рода жидкости и независимости от площади дна и от формы сосуда.
Выясняют зависимость давления от высоты столба и рода жидкости и независимости от площади дна и формы сосуда.
IV. Закрепление
Слайд 13- 14.Возьмем два сосуда. В одном из них находится вода, а в другом – подсолнечное масло. Уровень жидкости в обоих сосудах одинаков. Одинаковым ли будет давление этих жидкостей на дно сосудов?
Еще один пример. Имеются три различных по форме сосуда. В них до одного уровня налита одна и та же жидкость. Будет ли одинаковым давление на дно сосудов ?
Безусловно, нет. В формулу для расчета гидростатического давления входит плотность жидкости. Поскольку плотность подсолнечного масла меньше, чем плотность воды, а высота столба жидкостей одинакова, то масло будет оказывать на дно меньшее давление, чем вода
Да, давление будет одинаковым . Ведь в формуле гидростатического давления нет никакого упоминания о форме сосуда, площади его дна . Давление определяется исключительно плотностью жидкости и высотой ее столба.
- Куда бы вы перелили сок из литровой банки, чтобы его давление на дно стало больше: в пятилитровую кастрюлю или в литровую бутылку? Почему?
- В каком из сосудов давление, оказываемое жидкостью больше?
В литровую бутылку.
Одинаково
Назовите формулу для расчета давления жидкости на дно и стенки сосуда. Эта же формула используется для расчета давления газа на дно и стенки сосуда. Применим полученную формулу для решения задач. У вас на столах лежит карточка с алгоритмом решения задачи. Прочитайте алгоритм.
Алгоритм решения задач по физике
1. Внимательно прочитайте задачу.
2. Запишите в «Дано» все данные и правильно запишите искомую величину.
3. Сделайте перевод единиц в СИ, если это необходимо.
4. Сделайте чертёж или схему, если это необходимо.
5. Напишите формулу или закон, по которым находится искомая величина.
6. Запишите дополнительные формулы, если это необходимо.
7. Подставьте цифровые значения в окончательную формулу. Вычислите ответ. Проанализируйте его.
8. Запишите ответ.
9. Похвалите себя
Задача 1. Определите давление нефти на дно цистерны, если высота столба нефти 10 м, а плотность ее 800 кг/м³
Задача 2. Определите высоту столба керосина, который оказывает давление на дно сосуда равное 8000 Па.
Решение на слайде 16-17
Слайд 18 . Самостоятельная работа по вариантам.
Решение на слайде 19-20
Подведение итогов. Рефлексия
Слайд 21. О чём говорит нам эта формула?
Можно рассчитать давление жидкости, налитой в сосуд любой формы
Мы получили формулу для нахождения давления жидкости на дно и стенки сосуда. Этой формулой можно пользоваться и для расчета давления в объеме жидкости на заданной глубине. Она может быть использована для определения глубины погружения аквалангиста, при расчете конструкции батискафов, подводных лодок, для решения множества других научных и инженерных задач
Скажите, о чем мы говорили сегодня на уроке?
Продолжите предложение
На уроке для себя я сделал открытие, что
Формула для расчета давления жидкости на дно и стенки сосуда
Слайд 22. Домашнее задание.§40. Упр.17(1,2)
Ответ. Давление на дно зависит от плотности и высоты столба жидкости.
Можно вычислить давление на стенки сосуда (так как давление на одной и той же глубине одинаково по всем направлениям.)
О давлении жидкости на дно и стенки сосуда
давление жидкости на дно и стенки сосуда зависит от высоты и плотности жидкости
Записывают
Формировать навыки самоорганизации
Источник
