Задачи на давление газа в сосуде

Содержание:
- § 1 Повторение необходимых формул
- § 2 Решение задач
- § 3 Важно запомнить
§ 1 Повторение необходимых формул
В этом уроке мы рассмотрим решение задач на расчет давления в жидкостях и газах, атмосферное давление и законы сообщающихся сосудов.
Для решения задач нам нужно вспомнить формулы: давление равно отношению силы, действующей перпендикулярно поверхности, к площади поверхности:

Сила давления равна весу P = mg, площадь поверхности прямоугольной формы S = ab.
Давление в жидкостях и газах зависит от плотности и высоты столба жидкости или газа:
p = gρh.
Нам также пригодится знание нормального атмосферного давления: 760 мм рт.ст. = 101300 Па = 1 013гПа. Перевод атмосферного давления в международную систему единиц: 1 мм рт.ст. = 133,3 Па.
При решении задач на сообщающиеся сосуды нам нужно помнить, что при равенстве давлений поверхности однородной жидкости находятся на одном уровне, поверхности разнородных жидкостей устанавливаются на высоте, обратно пропорциональной их плотностям.
§ 2 Решение задач
Рассмотрим решение первой задачи:
Определите глубину погружения батискафа, если на его иллюминатор площадью 0,12 м2 давит вода с силой 1,9 МН.
Запишем условие задачи: площадь иллюминатора S = 0,12 м3, сила давления F = 1,9 МН = 1 900 000 Н в системе СИ, плотность морской воды ρ = 1030 кг/м3. Найти глубину погружения h.

Ответ: глубина погружения батискафа 1530 м
Ширина шлюза 10 м. Шлюз заполнен водой на глубину 5 м. С какой силой вода давит на ворота шлюза?
Запишем условие задачи: ширина шлюза а = 10 м, глубина воды h = 5 м, плотность воды ρ = 1000 кг/м3. Найти силу давления F на ворота шлюза.
Решение: Силу давления воды можем найти из формулы давления. Выразим: F = pS. В этой формуле p – давление воды. Если бы нам нужно было найти силу давления воды на дно реки, то мы учли бы всю высоту столба воды над дном. В этой задаче требуется найти силу давления на ворота, т.е. на стенку сосуда. Давление воды на верхнюю и нижнюю части стенки неодинаково, так как давление жидкости зависит от высоты столба жидкости. В таких случаях определяют среднее значение силы давления. Для этого силу давления, испытываемую воротами шлюза на максимальной глубине, делят на 2. Итак, средняя сила давления воды на ворота шлюза (на стенки сосуда) F = pS/2.
Ворота шлюза прямоугольной формы, поэтому S = ab = ah = 10 м · 5 м = 50 м2.

Ответ: сила давления воды на ворота 1250 кН
Каково показание барометра на уровне высоты Останкинской телебашни (540 м), если у поверхности земли нормальное атмосферное давление?
Запишем условие задачи. Известна высота башни h = 540 м, p1 – нормальное атмосферное давление 760 мм рт. ст., в системе СИ 101 300 Па. Найти давление на высоте: p2.
Решение. Измерениями установлено, что в среднем через каждые 12 м высоты атмосферное давление уменьшается на 1 мм рт.ст. Составим пропорцию, обозначим за х изменение давления на высоте 540 м. Тогда х = 540 м умножаем на 1 мм рт.ст. и делим на 12 м = 45 мм рт.ст.
Вычтем ответ из значения давления на поверхности земли: 760 – 45 мм рт.ст. = 715 мм рт.ст. Выразим ответ в международной системе единиц: 1 мм рт.ст. = 133, 3 Па. Тогда 715 мм.рт.ст. умножим на 133,3, получим 95 309,5 Па.

Ответ: давление на высоте 540 м составляет 95 309,5 Па
В правое колено сообщающихся сосудов налит керосин, а в левое – вода. Высота керосина 20 см. Определите, на сколько уровень керосина выше верхнего уровня воды.

§ 3 Важно запомнить
Чтобы найти давление тела на опору, надо силу давления (вес тела) разделить на площадь опоры:
Из формулы давления можно найти силу давления (вес тела) F = pS и площадь поверхности, на которую тело оказывает давление:
Давление в жидкостях и газах определяется по формуле p = gρh . Из этой формулы можно найти высоту столба жидкости или газа:
Две формулы
можно использовать вместе в одной задаче для расчета неизвестных величин, характеризующих жидкости или газы.
Нормальное атмосферное давление равно 760 мм рт.ст. или 101 300 Па.
Соотношение между единицей Паскаль и мм рт.ст.: 1 мм рт.ст. = 133,3 Па.
Список использованной литературы:
- Волков В.А. Поурочные разработки по физике: 7 класс. – 3-е изд. – М.: ВАКО, 2009. – 368 с.
- Волков В.А. Тесты по физике: 7-9 классы. – М.: ВАКО, 2009. – 224 с. – (Мастерская учителя физики).
- Кирик Л.А. Физика -7. Разноуровневые самостоятельные и контрольные работы. – М.: Илекса, 2008. – 192 с.
- Контрольно-измерительные материалы. Физика: 7 класс / Сост. Зорин Н.И. – М.: ВАКО, 2012. – 80 с.
- Марон А.Е., Марон Е.А. Физика. 7 Дидактические материалы. – М.: Дрофа, 2010. – 128 с.
- Перышкин А.В. Физика. 7 класс – М.: Дрофа, 2011.
- Тихомирова С.А. Физика в пословицах и поговорках, стихах и прозе, сказках и анекдотах. Пособие для учителя. – М.: Новая школа, 2002. – 144 с.
- Я иду на урок физики: 7 класс. Часть III: Книга для учителя. – М.: Издательство «Первое сентября”, 2002. – 272 с.
Источник
Задача 41.
Смешивают 0,04м3 азота, находящегося под давлением 96кПа (720мм. рт. ст.), с 0,02м3 кислорода. Общий объем смеси 0,06м3, а общее давление 97,6кПа (732мм. рт. ст.). Каким было давление взятого кислорода?
Решение:
По условию задачи объём азота увеличился в 1,5 раза (0,06/0,04 = 1,5), а объём кислорода – в 3 раза (0,06/0,02 = 3). Во столько же раз уменьшились парциальные давления газов.
Следовательно,
Согласно закону парциальных давлений, общее давление смеси газов, не вступающих во взаимодействие друг с другом, равно сумме парциальных давлений газов, составляющих систему (смесь). Отсюда Исходя из того, что объём кислорода до смешения был в три раза больше, чем после смешения, рассчитаем давление кислорода до смешения:
Ответ: Робщ. = 100,8кПа.
Задача 42.
Газовая смесь приготовлена из 2л Н2 (Р = 93,3 кПа) и 5л CH4 (Р = 112 кПа). Объем смеси равен 7л. Найти парциальные давления газов и общее давление смеси.
Решение:
По условию задачи объём водорода увеличился в 3,5 раза (7/2 = 3,5), а объём метана – в 1,4 раза (7/5 = 1,4). Во столько же раз уменьшились парциальные давления газов.
Согласно закону парциальных давлений, общее давление смеси газов, не вступающих во взаимодействие друг с другом, равно сумме парциальных давлений газов, составляющих систему (смесь).
Отсюда:
Ответ:
Задача 43.
Газовая смесь состоит из NO и СО2. Вычислить объемное содержание газов в смеси (в %), если их парциальные давления равны соответственно 36,3 и 70,4 кПа (272 и 528мм. рт. ст.).
Решение:
Согласно закону Дальтона парциальное давление данного газа прямо пропорционально его мольной доли на общее давление смеси газов:
где Р(смеси) – общее давление смеси; Р(А) – парциальное давление данного газа; (A) – мольная доля данного газа.
Согласно закону парциальных давлений, общее давление смеси газов, не вступающих во взаимодействие друг с другом, равно сумме парциальных давлений газов, составляющих систему (смесь).
Отсюда:
Ответ: 34,02%NO; 65,98%CO.
Задача 44.
В закрытом сосуде вместимостью 0,6м3 находится при 0 °С смесь, состоящая из 0,2кг СО2, 0,4кг 02 и 0,15кг СН4. Вычислить: а) общее давление смеси; б) парциальное давление каждого из газов; в) процентный состав смеси по объему.
Решение:
Вычислим общее количество газов в смеси по уравнению:
, где
– количество газа, кмоль; m – масса газа, кг; М – молекулярная масса газа, кг/моль. Тогда:
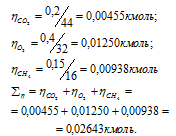
а) Общее давление смеси газов определяем по уравнению:
Тогда:
б) Парциальные давления газов рассчитываем по уравнению:
где Rk и k , соответственно, парциальное давление, и количество газа в смеси.
Тогда
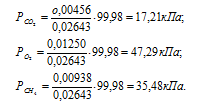
в) Парциальные объёмы газов рассчитаем по уравнению:
Тогда
Отношение парциальных (приведённых) объёмов отдельных газов к общему объёму смеси называется объёмной долей и определяется по формуле:
Тогда
Ответ:
Задача 45.
Газовая смесь приготовлена из 0,03м3 СН4, 0,04м3 Н2 и 0,01м3 СО. Исходные давления СН4, Н2 и СО составляли ответственно 96, 84 и 108,8 кПа (720, 630 и 816мм рт. ст.). Объем смеси равен 0,08м3. Определить парциальные давления газов и общее давление смеси.
Решение:
По условию задачи объём метана увеличился после смешения в 2,67 раза (0,08/0,03 = 2,67), объём водорода – в 2 раза (0,08/0,04 = 2), а объём угарного газа – в 8 раз (0,08/0,01 = 8). Во столько же раз уменьшились парциальные давления газов. Следовательно,
Согласно закону парциальных давлений, общее давление смеси газов, не вступающих во взаимодействие друг с другом, равно сумме парциальных давлений газов, составляющих систему (смесь).
Отсюда:
Ответ:
Задача 46.
В газометре над водой находятся 7,4л кислорода при 23 °С и давлении 104,1 кПа (781 мм. рт. ст.). Давление насыщенного водяного пара при 23 °С равно 2,8 кПа (21мм. рт. ст.). Какой объем займет находящийся в газометре кислород при нормальных условиях?
Решение:
Парциальное давление кислорода равно разности общего давления и парциального давления паров воды:
Обозначив искомый объём через и, используя объединённое уравнение закона Бойля- Мариотта и Гей-Люссака, находим:
где Р и V – давление и объём газа при температуре Т = 296К (273 +23 = 296); Р0 = 101,325кПа; Т0 = 273К; Р = 104,1кПа; – объём газа при н.у.
Ответ: V0 =6,825л.
Источник
Решебник к сборнику задач по физике для 7- 9 классов, Перышкин А.В.
405. Поднимающиеся со дна водоема пузырьки воздуха увеличиваются в объеме по мере приближения к поверхности. Почему?
С приближением к поверхности, давление воды на пузырек падает.
406. Воду из узкого высокого стакана перелили в широкую кастрюлю. Как изменилось давление воды на дно?
Давление уменьшилось, поскольку уменьшилась высота водяного столба.
407. На рисунке 44 изображен старинный опыт: в крышку бочки, наполненную доверху водой, была вставлена высокая узкая трубка. Когда в трубку налили воды, бочка разорвалась. Объясните, почему небольшое количество воды, которую пришлось налить в трубку, могло разорвать бочку?
Давление на стенки бочки будет зависеть от плотности жидкости и высоты водяного столба и не зависит от площади поперечного сечения сосуда.
408. В сосуд налили слой воды высотой 15 см. каково давление этого слоя на дно сосуда?
409. Чему равно давление воды на глубине 50 см?
410. Банка высотой 50 см наполнена водою. Определите давление на 1 см2 дна банки.
411. В мензурку, площадь дна которой 20 см2 , налита вода до высоты 10 см. сколько граммов воды налито? Чему равно давление воды на дно мензурки?
412. Высота уровня воды в водопроводе 10 м (рис.45). Одинаковы ли давления на стенки трубы на различных высотах? Каково давление воды у нижнего конца трубы?
413. Каково давление на дверцу в шлюзовых воротах на глубине 12 м (рис. 46)?
414. В стакан высотой 10 см налита доверху ртуть. Вычислить давление на дно стакана.
415. Вычислите давление столбика ртути высотой 76 см.
416. Поршневой насос может произвести давление 5·105 Па. На какую высоту можно поднять воду этим насосом?
417. В трех сосудах налита вода до одной и той же высоты (рис. 47). В каком сосуде налито больше воды? В каком сосуде больше давление на дно?
Давление во всех сосудах на дно одинаково.
418. Внутрь жидкости погружен брусок (рис 48). Одинаковые ли давления испытывают боковые стенки бруска (левая и правая, передняя и задняя)? Одинаковые ли давления испытывают верхняя и нижняя грани бруска?
Боковые стенки испытывают одинаковое давление; верхняя и нижняя – разное.
419. Рассмотрите рисунок 48. Высота погруженного бруска АК=5 см. На сколько больше давление на грани MNKL, чем на ABCD, если брусок помещен в воду на глубину 12 см (до нижней грани)?
420. Если в подводной части судна появилась пробоина, то на эту пробоину накладывают «пластырь» – кусок паруса, который давлением воды прижимается к корпусу судна и не пропускает в пробоину воду. Определите силу, с которой прижимается пластырь, если площадь пробоины 0,5 м2 , а глубина, на которой сделана пробоина , 2 м.
421. В сталелитейном производстве «изложницей» называется чугунный стакан без дна, в который выливают Расплавленный металл (рис. 49). Верхнее отверстие изложницы немного меньше нижнего для того, чтобы можно было изложницу снять с отвердевшего слитка, когда остынет металл. Чтобы металл снизу не выливался, изложницы ставят на плоское основание и делают их очень массивными. На рисунке 49 слева изображена изложница, справа – подъем изложницы с отлитого слитка.
Определите силу давления, которую производит на подложку изложницы налитый чугун, если высота изложницы 1,5 м, а площадь нижнего основания 1600 см2. Плотность чугуна 7,2 г/см3.
422. Для спуска водолаза на очень большую глубину применяется специальный металлический скафандр (рис . 50). Какую силу давления должен выдержать этот скафандр на глубине 300 м, если общая поверхность скафандра составляет 2,5 м2 ?
423. Для выпуска расплавленного металла из литейного ковша делают на дне ковша отверстие, закрываемое специальной пробкой из огнеупорного металла. Определите давление расплавленной стали на пробку, если высота налитого металла 2 м, а плотность расплавленной стали 7,3 г/см³.
424. Как велика должна быть высота столба ртути и столба спирта, если этот столб производит давление в 105 Па?
425. Определите давление воды на стенки котла водяного отопления, если высота труб 20 м?
426.Вычислите разность давлений в трубах водопровода на нижнем этаже здания и на этаже, расположенном выше на 15 м?
427. Батискаф спустился в море на глубину в 50 м. Каково давление на поверхность батискафа на данной глубине?
428. Давление в водопроводе 4·105 Па. С какой силой давит вода на пробку, закрывающую отверстие трубы, если площадь отверстия 4 см2 ?
429. Давление в трубах водопровода 4·105 Па. На какую высоту будет бить вода из пожарной трубы, присоединенной к этому водопроводу, если не принимать во внимание сопротивление воздуха и трение воды в трубах?
430. Человек стоит на кожаном мешке с водой (рис. 51). Рассчитайте, на какую высоту поднимается вода в трубке, если масса человека 75 кг, площадь соприкасающаяся с мешком поверхности платформы 1000 см2.
431. Футбольная камера соединена с вертикальной стеклянной трубкой. В камере и трубке находится спирт. На камеру положили диск, а на него – гирю массой 5 кг. Высота столба спирта в трубке 1 м. Какова площадь соприкосновения диска с камерой?
Источник
Задача 28.
При 17°С некоторое количество газа занимает объем 580 мл. Какой объем займет это же количество газа при 100°С, если давление его останется неизменным?
Решение:
По закону Гей – Люссака при постоянном давлении объём газа изменяется прямо пропорционально абсолютной температуре (Т):
V2 – искомый объём газа;
T2 – соответствующая V2 температура;
V1 – начальный объём газа при соответствующей температуре Т1.
По условию задачи V1 = 580мл; Т1 = 290К (273 + 17 = 290) и Т2 = 373К (273 + 100 = 373). Подставляя эти значения в выражение закона Гей – Люссака, получим:
Ответ: V2 = 746мл.
Задача 29.
Давление газа, занимающего объем 2,5л, равно 121,6 кПа (912мм рт. ст.). Чему будет равно давление, если, не изменяя температуры, сжать газ до объема в 1л?
Решение:
Согласно закону Бойля – Мариотта, при постоянной температуре давление, производимое данной массой газа, обратно пропорционально объёму газа:
Обозначив искомое давление газа через Р2, можно записать:
Ответ: Р2 = 304кПа (2280мм.рт.ст.).
Задача 30. На сколько градусов надо нагреть газ, находящийся в закрытом сосуде при 0 °С, чтобы давление его увеличилось вдвое?
Решение:
При постоянном объёме давление газа изменяется прямо пропорционально температуре:
По условию задачи Т1 = 0 °С + 273 = 273К; давление возросло в два раза: Р2 = 2Р1.
Подставляя эти значения в уравнение, находим:
Ответ: Газ нужно нагреть на 2730С.
Задача 31.
При 27°С и давлении 720 мм.рт. ст. объем газа равен 5л. Кой объем займет это же количество газа при 39°С и давлении 104кПа?
Решение:
Зависимость между объёмом газа, давлением и температурой выражается общим уравнением, объединяющим законы Гей-Люссака и Бойля-Мариотта:
где Р и V – давление и объём газа при температуре Т; Р0 и V0 – давление и объём газа при нормальных условиях. Данные задачи: V = 5л; Т = 298К (273 + 25 = 298); Р = 720 мм.рт.ст. (5,99 кПа); Р0 = 104 кПа; Т = 312К (273 + 39 = 312); Т = 273К. Подставляя данные задачи в уравнение, получим:
Ответ: V0 = 4,8л
Задача 32.
При 7°С давление газа в закрытом сосуде равно 96,0 кПа. Каким станет давление, если охладить сосуд до -33 °С?
Решение:
При постоянном объёме давление газа изменяется прямо пропорционально абсолютной температуре:
Обозначим искомое давление через Р2, а соответствующую ему температуру через Т2. По условию задачи Р1 = 96,0 кПа; Т1 = 280К (273 + 7 = 280); Т2 = 240К (273 – 33 = 240). Подставляя эти значения в уравнение, получим:
Ответ: Р2 = 82,3кПа.
Задача 33.
При нормальных условиях 1г воздуха занимает объем 773 мл. Какой объем займет та же масса воздуха при 0 °С и )и давлении, равном 93,3 кПа (700мм. рт. ст.)?
Решение:
Зависимость между объёмом газа, давлением и температурой выражается общим уравнением, объединяющим законы Гей-Люссака и Бойля-Мариотта:
где Р и V – давление и объём газа при температуре Т; Р0 и V0 – давление и объём газа при нормальных условиях. Данные задачи: Р0 = 101,325кПа; V0 = 773мл; Т0 = 298К (273 + 25 = 298); Т = 273К; Р = 93,3кПа. Подставляя данные задачи и преобразуя уравнение, получим:
Ответ: V = 769, 07 мл.
Задача 34.
Давление газа в закрытом сосуде при 12°С равно 100 кПа (750мм рт. ст.). Каким станет давление газа, если нагреть сосуд до 30°С?
Решение:
При постоянном объёме давление газа изменяется прямо пропорционально абсолютной температуре:
Обозначим искомое давление через Р2, а соответствующую ему температуру через Т2. По условию задачи Р1 = 100 кПа; Т1 = 285К (273 + 12 = 285); Т2 = 303К (273 + 30 = 303). Подставляя эти значения в уравнение, получим:
Ответ: Р2 = 106,3кПа.
Задача 35.
В стальном баллоне вместимостью 12л находится при 0°С кислород под давлением 15,2 МПа. Какой объем кислорода, находящегося при нормальных условиях можно получить из такого баллона?
Решение:
Зависимость между объёмом газа, давлением и температурой выражается общим уравнением, объединяющим законы Гей-Люссака и Бойля-Мариотта:
где Р и V – давление и объём газа при температуре Т; Р0 и V0 – давление и объём газа при нормальных условиях. Данные задачи: V = 12л; Т = 273К (273 + 0 = 2273); Р =15,2МПа); Р0 = 101,325кПа; Т0 = 298К (273 + 25 = 298). Подставляя данные задачи в уравнение, получим:
Ответ: V0 = 1,97м3.
Задача 36.
Температура азота, находящегося в стальном баллоне под давлением 12,5 МПа, равна 17°С. Предельное давление для баллона 20,3МПа. При какой температуре давление азота достигнет предельного значения?
Решение:
При постоянном объёме давление газа изменяется прямо пропорционально абсолютной температуре:
Обозначим искомое давление через Р2, а соответствующую ему температуру через Т2. По условию задачи Р1 = 12,5МПа; Т1 = 290К (273 + 17 = 290); Р2 = 20,3МПа. Подставляя эти значения в уравнение, получим:
Ответ: Т2 = 1980С.
Задача 37.
При давлении 98,7кПа и температуре 91°С некоторое количество газа занимает объем 680 мл. Найти объем газа при нормальных условиях.
Решение:
Зависимость между объёмом газа, давлением и температурой выражается общим уравнением, объединяющим законы Гей-Люссака и Бойля-Мариотта:
где Р и V – давление и объём газа при температуре Т; Р0 и V0 – давление и объём газа при нормальных условиях. Данные задачи: Р0 = 101,325кПа; V = 680мл; Т0 = 298К (273 + 25 = 298); Т = 364К (273 + 91 = 364); Р = 98,7кПа. Подставляя данные задачи и преобразуя уравнение, получим:
<
Ответ: V0 = 542,3мл.
Задача 38.
При взаимодействии 1,28г металла с водой выделилось 380 мл водорода, измеренного при 21°С и давлении 104,5кПа (784мм рт. ст.). Найти эквивалентную массу металла.
Решение:
Находим объём выделившегося водорода при нормальных условиях, используя уравнение:
где Р и V – давление и объём газа при температуре Т = 294К (273 +21 = 294); Р0 = 101,325кПа; Т0 = 273К; Р = 104,5кПа. Подставляя данные задачи в уравнение,
получим:
Согласно закону эквивалентов, массы (объёмы) реагирующих друг с другом веществ m1 и m2 пропорциональны их эквивалентным массам (объёмам):
Мольный объём любого газа при н.у. равен 22,4л. Отсюда эквивалентный объём водорода равен 22,4 : 2 = 11,2л или 11200 мл. Тогда, используя формулу закона эквивалентов, рассчитаем эквивалентную массу металла:
Ответ: mЭ(Ме) = 39,4г/моль.
Задача 39.
Как следует изменить условия, чтобы увеличение массы данного газа не привело к возрастанию его объема: а) понизить температуру; б) увеличить давление; в) нельзя подобрать условий?
Решение:
Для характеристики газа количеством вещества (n, моль) применяется уравнение РV = nRT, или – это уравнение Клапейрона-Менделеева. Оно связывает массу (m, кг); температуру (Т, К); давление (Р, Па) и объём (V, м3) газа с молярной массой (М, кг/моль).
Тогда из уравнения Клапейрона-Менделеева объём газа можно рассчитать по выражению:
Отсюда следует, что V = const, если при увеличении массы (m) газа на некоторую величину будет соответственно уменьшена температура (T) системы на некоторое необходимое значение. Объём системы также не изменится при постоянной температуре, если при увеличении массы (m) газа на некоторую величину будет соответственно увеличено давление (P) системы на необходимую величину.
Таким образом, при увеличении массы газа объём системы не изменится, если понизить температуру системы или же увеличить давление в ней на некоторую величину.
Ответ: а); б).
Задача 40.
Какие значения температуры и давления соответствуют нормальным условиям для газов: а) t = 25 °С, Р = 760 мм. рт. ст.; б) t = 0 °С, Р = 1,013 • 105Па; в) t = 0°С, Р = 760 мм. рт. ст.?
Решение:
Состояние газа характеризуется температурой, давлением и объёмом. Если температура газа равна 0 °С (273К), а давление составляет 101325 Па (1,013 • 105) или 760 мм. рт. ст., то условия, при которых находится газ, принято считать нормальными.
Ответ: б); в).
Источник
