Задачи на нагревание сосуда
Задачи на количество теплоты с решениями
Формулы, используемые на уроках «Задачи на количество теплоты,
удельную теплоемкость».
1 г = 0,001 кг; 1 т = 1000 кг; 1 кДж = 1000 Дж; 1 МДж = 1000000 Дж
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1. В железный котёл массой 5 кг налита вода массой 10 кг. Какое количество теплоты нужно передать котлу с водой для изменения их температуры от 10 до 100 °С?
При решении задачи нужно учесть, что оба тела – и котёл, и вода – будут нагреваться вместе. Между ними происходит теплообмен. Их температуры можно считать одинаковыми, т. е. температура котла и воды изменяется на 100 °С – 10 °С = 90 °С. Но количества теплоты, полученные котлом и водой, не будут одинаковыми. Ведь их массы и удельные теплоёмкости различны.

Задача № 2. Смешали воду массой 0,8 кг, имеющую температуру 25 °С, и воду при температуре 100 °С массой 0,2 кг. Температуру полученной смеси измерили, и она оказалась равной 40 °С. Вычислите, какое количество теплоты отдала горячая вода при остывании и получила холодная вода при нагревании. Сравните эти количества теплоты.

Задача № 3. Стальная деталь массой 3 кг нагрелась от 25 до 45 °С. Какое количество теплоты было израсходовано?

Задача № 4. В сосуде содержится 3 л воды при температуре 20 °С. Сколько воды при температуре 45 °С надо добавить в сосуд, чтобы в нём установилась температура 30 °С? Необходимый свободный объём в сосуде имеется. Теплообменом с окружающей средой пренебречь

Задача № 5. На сколько градусов изменилась температура чугунной детали массой 12 кг, если при остывании она отдала 648000 Дж теплоты?

Задача № 6. По графику определите удельную теплоёмкость образца, если его масса 50 г.
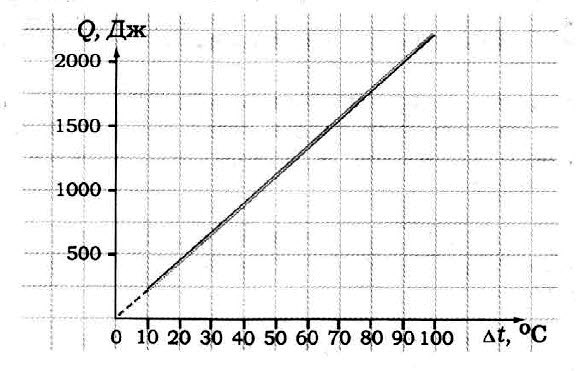

Задача № 7. Для нагревания медного бруска массой 3 кг от 20 до 30 °С потребовалось 12000 Дж теплоты. Какова удельная теплоемкость меди?

Задача № 8. Нагретый камень массой 5 кг, охлаждаясь в воде на 1 °С, передает ей 2,1 кДж энергии. Чему равна удельная теплоемкость камня?
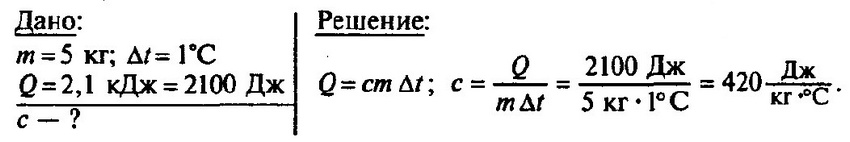
Задача № 9. Какое количество теплоты потребуется для нагревания на 1 °С воды объемом 0,5 л; олова массой 500 г; серебра объемом 2 см3; стали объемом 0,5 м3; латуни массой 0,2 т?

Задача № 10. Какое количество теплоты получили алюминиевая кастрюля массой 200 г и находящаяся в ней вода объемом 1,5 л при нагревании от 20 °С до кипения при температуре 100 °С?

Задача № 11. а) Воздух, заполняющий объем 0,5 л в цилиндре с легким поршнем, нагрели от 0 до 30 °С при постоянном атмосферном давлении. Какое количество теплоты получил воздух?
б) В порожнем закрытом металлическом баке вместимостью 60 м3 под действием солнечного излучения воздух нагрелся от 0 до 20 °С. Как и на сколько изменилась внутренняя энергия воздуха в баке? (Удельная теплоемкость воздуха при постоянном объеме равна 720 Дж/кг-°С.)

Задача № 12. ОГЭ Металлический цилиндр массой m = 60 г нагрели в кипятке до температуры t = 100 °С и опустили в воду, масса которой mв = 300 г, а температура tв = 24 °С. Температура воды и цилиндра стала равной Θ = 27 °С. Найти удельную теплоёмкость металла, из которого изготовлен цилиндр. Удельная теплоёмкость воды св = 4200 Дж/(кг К).

Задача № 13. В теплоизолированном сосуде сначала смешивают три порции воды 100 г, 200 г и 300 г с начальными температурами 20 °C, 70 °C и 50 °C соответственно. После установления теплового равновесия в сосуд добавляют новую порцию воды массой 400 г при температуре 20 °C. Определите конечную температуру в сосуде. Ответ дайте в °C, округлив до целого числа. Теплоёмкостью калориметра пренебрегите.
Решение.

Ответ: 39 °С.
Задача № 14. (повышенной сложности) Стальной шарик радиусом 5 см, нагретый до температуры 500 ˚С, положили на лед, температура которого 0 ˚С. На какую глубину погрузится шарик в лед? (Считать, что шарик погрузился в лед полностью. Теплопроводностью шарика и нагреванием воды пренебречь.)
Дано: R = 0,05 м; t1 = 500 ˚С; t2 = 0 ˚С;
ρ1 (плотность стали) = 7800 кг/м3.;
ρ2 (плотность льда) = 900 кг/м3.
c (удельная теплоемкость стали) = 460 Дж/кг •˚С,
λ (удельная теплота плавления льда) = 3,3 • 105 Дж/кг,
Найти: h – ?

Краткая теория для решения Задачи на количество теплоты.

Конспект урока «Задачи на количество теплоты».
Посмотреть конспект урока по теме «Количество теплоты. Удельная теплоемкость»
Следующая тема: «ЗАДАЧИ на сгорание топлива с решениями».
Источник
Эти задачи я использовала при подготовке к олимпиаде семи- и восьмиклассников. Также можно решать их для подготовки к ЕГЭ, для более глубокого проникновения в тему.
Задача 1. На дне глубокой шахты лежало 700 кг льда при температуре С. В шахту сбросили 678 л горячей воды. В момент падения на лед ее температура равнялась С, весь лед при этом растаял. На какой наименьшей глубине находился в шахте лед, если удельная теплоемкость воды равна 4,2 кДж/(кгС), а удельная теплота плавления льда равна кДж/кг? Трением о воздух в процессе падения пренебречь.
Определим, сколько нужно джоулей, чтобы растопить весь лед:
Теперь посмотрим, сколько джоулей отдаст вода, если остынет на С, то есть до нулевой температуры:
Здесь подставлена масса воды, думаю, всем понятно, что 678 л воды имеют массу 678 кг?
То есть тепла, связанного с остыванием воды, нам не хватит, чтобы растопить весь лед. Поэтому надо подумать, откуда взялась разница между и . Вода, падая, набрала скорость, то есть обладала кинетической энергией. Эта энергия и преобразовалась в тепло. А превратилась эта энергия в кинетическую из потенциальной, которой вода обладала вверху. Тогда
Ответ: м – минимальная высота падения.
Задача 2. Сосуд наполнен до краев водой массой кг с температурой С. В него аккуратно опускают кусок льда массой кг, имеющий температуру С. Какая температура установится в сосуде? Удельная теплоемкость воды c = 4200 Дж/(кгC), удельная теплота плавления льда кДж/кг. Тепловыми потерями пренебречь.
Так как сосуд наполнен до самых краев, то часть воды выльется. Определим, какая это будет часть. Масса вылившейся воды совпадает с массой льда. В этом можно убедиться через давление на дно: если лед уже плавает в сосуде, то, растаяв, он тем самым давление на дно не изменит, а значит, объем вылившейся воды совпадает с объемом погруженной части льда или, попросту, равны массы льда и вылившейся воды.
Таким образом, вылилось 2,1 л воды. Зная плотность воды, находим, что масса этого объема воды 2,1 кг. Тогда воды в сосуде осталось
Составим уравнение теплового баланса: потребителями тепла будут лед (на таяние) и получившаяся изо льда вода (на согрев). Отдаст это тепло та вода, что была в сосуде ().
Ответ: .
Задача 3. В бассейн по трубе, в которой установлен нагреватель мощностью МВт, подается вода из резервуара. Температура воды в резервуаре С. В первый раз пустой бассейн заполняется за время мин, при этом температура воды после заполнения С. Во второй раз в бассейне было изначально некоторое количество воды при температуре С. Оставшуюся часть заполняли также время мин. Температура воды после заполнения оказалась C. Сколько воды первоначально было в бассейне во втором случае? Остыванием воды в бассейне пренебречь. Теплоемкость воды Дж/кгС.
Мощность нагревателя постоянна, следовательно, он от дал в обоих случаях одно и то же количество теплоты, так как работал одно и то же время. В первом случае тепло пошло на нагрев полного бассейна (вода нагрелась с 5 до 20 градусов, то есть на 15):
Откуда можно узнать, сколько всего воды по массе помещается в бассейне.
Итак, в бассейне 20 тонн воды. Пусть часть воды, которая была в бассейне во второй раз, равна , а часть, которую мы грели, . Следовательно,
Теперь составляем уравнение баланса. Воду массой мы нагрели на 10 градусов, а часть – на 20.
Так как
То
Ответ: 10000 кг, или 10 т
Задача 4. На плите стоит кастрюля с водой. При нагревании температура воды увеличилась от C до C за одну минуту. Какая доля теплоты, получаемой водой при нагревании, рассеивается в окружающем пространстве, если время остывания той же воды от C до C равно 9,0 минутам?
Так как вода нагрелась в первом случае на 5 градусов, и потом остыла на те же пять градусов, то приобретенное и потерянное количество теплоты – одно и то же. Сначала вода получала тепло от плиты, но и теряла его тоже:
Потом – только теряла тепло:
Тогда
Ответ: 0,1
Задача 5. В теплоизолированном сосуде находится смесь льда массой кг и воды. После начала нагревания температура смеси оставалась постоянной в течение времени мин, а затем за время мин повысилась на С. Определите массу смеси, если считать, что количество теплоты, получаемое системой в единицу времени, постоянно. Удельная теплота плавления льда кДж/кг, а удельная теплоемкость воды кДж/(кгК). Теплоемкостью сосуда пренебречь.
Сначала шло таяние льда, так как температура не менялась. Тогда можно записать, что на плавление льда пошло тепло, равное:
Потом нагревалась вода, которая была в сосуде и вода, получившаяся изо льда:
Так как – постоянно, то
Ответ: 3 кг
Задача 6. Кусок льда с вмерзшими в него свинцовыми дробинками общей массой 200 г осторожно опускают в стакан калориметра, доверху наполненный водой. Часть воды при этом выливается и в дальнейшем теплообмене не участвует. Когда система пришла в состояние теплового равновесия, оказалось, что температура воды в калориметре С . Начальные температуры воды С, льда С. Масса воды в калориметре была 1,2 кг. Определите объемное содержание свинца в куске льда. Теплоемкостью калориметра пренебречь.
Предположим, что лед со свинцом будет плавать, а не тонуть. Тогда по закону Архимеда он вытеснит такой объем воды, что вес этого объема 200 г. То есть воды останется литр. Запишем уравнение теплового баланса для этой системы.
Зная, что
Выразим массу льда (или свинца)
И подставим в уравнение теплового баланса:
Упрощая это выражение и подставляя все константы, получим
Тогда
Объемное содержание свинца равно
Ответ: .
Задача 7. Волшебник готовит в аптекарском стакане емкостью 0,3 л целебную смесь. Он налил в стакан доверху живую воду температурой С. К сожалению, стакан с водой остывает на С за пять минут. Для того, чтобы смесь не остывала, волшебник капает в стакан обыкновенную теплую воду с температурой С. Масса одной капли 0,2 г. Сколько капель в минуту нужно капать в стакан, чтобы температура в нем поддерживалась равной С? На сколько нагреется за одну минуту вода в стакане, если капать в три раза чаще? Теплоемкости живой и обычной воды совпадают. Лишняя вода выливается из носика.
Будем считать, что как только капля обычной воды попадает в стакан, из его носика сразу же падает капля живой, и более в теплообмене не участвует.
Давайте определим, какое количество теплоты теряет стакан за пять минут. Масса воды в нем нам известна, следовательно,
Следовательно, простая вода должна «принести» 1260 Дж, чтобы стакан не остывал. При этом простая вода охлаждается на градусов. Тогда
Приравнивая количества теплоты, имеем:
Разделим эту массу на массу капли, чтобы узнать их количество:
Так как капать надо в течение 5 минут, то получается, по 15 капель в минуту.
Если капать в три раза чаще, то число капель в минуту будет равняться 45, причем первые 15 капель в минуту будут приносить энергию, достаточную, чтобы поддерживать уровень температуры, а еще 30 капель уже будут нагревать воду в стакане. Следовательно, на нагрев пойдет Дж. Это количество тепла нагреет стакан массой 0,3 кг на
На 2 градуса за 5 минут, следовательно, на 0,4 градуса за минуту.
Ответ: а) 15 капель в минуту; б) на 0,4 градуса.
Задача 8. Теплоизолированный сосуд был до краев наполнен водой при температуре С. В середину этого сосуда быстро, но аккуратно опустили деталь, изготовленную из металла плотностью кг/м, нагретую до температуры С, и закрыли крышкой. После установления теплового равновесия температура воды в сосуде стала равна С. Затем в этот же сосуд, наполненный до краев водой при температуре С, вновь быстро, но аккуратно опустили две такие же детали, нагретые до той же температуры С, и закрыли крышкой. В этом случае после установления в сосуде теплового равновесия температура воды равна С. Чему равна удельная теплоемкость металла, из которого изготовлены детали? Плотность воды 1000 кг/м. Удельная теплоемкость воды Дж/(кг *К).
Запишем уравнение теплового баланса для обоих случаев. В первом случае из сосуда выльется объем воды, равный .
Во втором случае из сосуда выльется вода в количестве :
Выразим в обоих случаях и приравняем, таким образом мы исключим эту величину. Из первого уравнения:
Из второго уравнения:
Тогда
Объем детали сократится.
Подставим числа:
Подсчеты дают Дж/(кг*К)
Ответ: Дж/(кг*К).
Источник
Тема. Решение задач по теме «Фазовые превращения»
Цели:
Добиться понимания у учащихся понятия фаз вещества, показать, что, как правило, фазовые превращения сопровождаются поглощением или выделением энергии.
Ход занятия
Прежде всего, сформулировать понятие фазы. Повторить, при каких условиях вещество может переходить из одной фазы в другую.
Для проведения занятия учащимся предлагается несколько задач с объяснением их решения и задачи для самостоятельного решения.
Качественные вопросы
1. Что такое фаза вещества?
2. Сколько фаз вещества может существовать одновременно?
3. Что называется плавлением вещества?
4. Изменяется ли температура вещества при плавлении?
5. Что называется парообразованием?
6. Какие два способа парообразования существуют?
7. Что называется удельной теплоемкостью?
8. Что называется удельной теплотой плавления?
9. Что называется удельной теплотой парообразования?
10. Что такое критическая температура?
Примеры решения задач
Задача 1. На какую высоту можно было бы поднять груз m = 103 кг, если бы удалось полностью использовать энергию, освобождающуюся при остывании 1 л воды от t1 = 100° C до t2 = 20° C?
Решение
При остывании воды освобождается энергия
,
где m1 = rV – масса воды, с – удельная теплоемкость воды, равная 4,19×103 Дж/кг×град.
Для того чтобы поднять груз m на высоту hдолжна быть выполнена работа
.
Следовательно, ,
м.
Подстановка числовых данных приводит к ответу
м.
Ответ: м.
Задача 2. На сколько градусов нагреется вода, падая с высоты h, если k-ая часть выполненной при ее падении работы тратится на нагревание воды?
Решение
Работа, выполненная при падении с высоты h, равна потенциальной энергии, которую имела масса воды m на этой высоте.
; ;
.
Ответ: : .
Задача 3. Какое количество теплоты Q нужно затратить на превращение m = 2 кг льда, взятого при t1 = -10 °C в пар при температуре t2 = 100 °C?
Решение
На нагревание льда до 0 °С затрачивается количество теплоты ,
на плавление ml,
на нагревание получившейся воды ,
на ее испарение mr,
с1 – удельная теплоемкость льда, с1 = 2,1∙103 Дж/кг∙К;
l – удельная теплота плавления, l = 335∙103 Дж/кг;
r – удельная теплота парообразования, r = 2260∙103 Дж/кг;
с – теплоемкость воды, с = 4,19∙103 Дж/кг∙К.
.
Подстановка числовых данных приводит к ответу:
Дж.
Ответ: Q = 6,01∙106 Дж.
Задача 4. В сосуде, из которого быстро выкачивают воздух, находится небольшое количество воды при 0 °С. Из-за интенсивного испарения происходит постепенное замораживание воды. Какая часть первоначального количества воды может быть таким образом превращена в лед?
Решение
Пусть т – первоначальная масса воды, т1 – масса воды, превращающаяся в лед, т2 – масса воды, превращающаяся в пар. Теплота, необходимая для образования пара, может быть получена только за счет теплоты, выделяющейся при замерзании воды.
Обозначим выделяющуюся при замерзании воды теплоту , а теплоту пошедшую на образование пара – . Очевидно, что . Но , где l – удельная теплота плавления, а , где r – удельная теплота парообразования.
,
.
Учитывая, что , получим
.
Отсюда , .
Подставляя значения:
Дж/кг,
Дж/кг,
получим
.
Таким образом, в лед может быть превращено 0,87 первоначальной массы воды.
Ответ: .
Задача 5. Вода, температура которой °С, поставлена на электрическую плиту. Спустя время мин, вода закипела. Через какое время вода полностью испарится?
Решение
Теплота Q, необходимая для испарения воды, нагретой до кипения , где r – удельная скрытая теплота парообразования, т – масса воды.
Пусть от плиты за единицу времени поступает теплота q, тогда
(1)
Теплота , поступившая от плиты за время и нагревшая воду до температуры кипения , равно
,
где с – удельная теплоемкость воды.
Масса воды отсюда:
. (2)
Подставляя (2) в (1), получаем
.
.
Подставляя значения
Дж/кг.
Дж/кг,
получаем
час.
Ответ: час.
Задачи для самостоятельного решения
1. В бак, содержащий воду с массой кг при температуре °С, бросили кусок железа с массой кг, нагретый до температуры °С. При этом некоторая масса воды обратилась в пар. Конечная температура, установившаяся в баке, равна °С. Определить массу т воды, обратившейся в пар.
Ответ: кг.
2. Определить какую массу свинца т, взятого при °С, можно расплавить за счет теплоты, полученной при сгорании кг нефти, если к.п.д. нагревателя . Удельная теплота сгорания нефти МДж/кг.
Ответ: .
3. При помещении в переохлажденную воду небольшого кристаллика льда вода немедленно замерзает. Какая масса льда т образует из кг воды охлажденной до °С?
Ответ: кг.
4. В сосуде находилась вода при °С. Выкачивая из сосуда воздух, заморозили воду посредством собственного испарения. Какая часть воды испарилась, если притока извне нет?
Ответ: .
5. Лед массой т = 5 кг при °С опустили в воду при °С. Масса воды кг. Какую температуру будет иметь вода, когда весь лед растает?
Удельная теплоемкость воды Дж/кг×К; удельная теплоемкость льда Дж/кг×К; удельная теплота плавления льда Дж/кг.
Ответ: .
Рекомендуемая литература
1. Бутиков Е.И., Кондратьев А.С. Физика. Т.3. Строение и свойства вещества – Москва – Санкт-Петербург. Физматлит. Невский диалект. Лаборатория Базовых Знаний, 2001. С. 229-235.
2. Белолипецкий С.Н., Еркович О.С., Казаковцева В.А., Цвецинская Т.С. Задачник по физике – Москва. Физматлит, 2005.
3. Готовцев В.В. Лучшие задачи по механике и термодинамике. Москва-Ростов-на-Дону, Издательский центр «Март», 2004. С. 256-268.
Источник
