Задачи на проценты и сосуды

11. Сюжетные текстовые задачи
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
(blacktriangleright) Концентрация вещества в растворе (сплаве) – это процент содержания этого вещества в растворе (сплаве): [text{концентрация вещества}=dfrac{text{масса вещества}}{text{масса раствора}}cdot 100%]
(blacktriangleright) Заметим, что в задачах из данной подтемы зачастую удобно составлять уравнения относительно кислоты или активного вещества.
Задание
1
#846
Уровень задания: Равен ЕГЭ
Сергей смешал раствор, содержащий (20%) кислоты и раствор, содержащий (40%) той же кислоты. В итоге у него получился раствор, содержащий (32,5%) кислоты, причём объём полученного раствора (4) литра. Сколько литров раствора, содержащего (20%) кислоты, использовал Сергей при смешивании?
Пусть (x) литров раствора, содержащего (20%) кислоты использовал Сергей при смешивании, тогда
(4 – x) литров раствора, содержащего (40%) кислоты использовал Сергей при смешивании,
(dfrac{20}{100}x) – объём кислоты в растворе, содержащем (20%) кислоты, (dfrac{40}{100}(4 – x)) – объём кислоты в растворе, содержащем (40%) кислоты.
Так как в итоге кислоты оказалось (dfrac{32,5}{100} cdot 4 = 1,3) литра, то:
[dfrac{20}{100}x + dfrac{40}{100}(4 – x) = 1,3,] откуда находим (x = 1,5).
Ответ: 1,5
Задание
2
#844
Уровень задания: Равен ЕГЭ
Один газ в сосуде А содержал (21%) кислорода, второй газ в сосуде В содержал (5%) кислорода. Масса первого газа в сосуде А была больше массы второго газа в сосуде В на 300 г. Перегородку между сосудами убрали так, что газы перемешались и получившийся третий газ теперь содержит (14,6%) кислорода. Найдите массу третьего газа. Ответ дайте в граммах.
Пусть (x) грамм – масса второго газа, тогда
(x + 300) грамм – масса первого газа,
(dfrac{21}{100}(x + 300)) грамм – масса кислорода в первом газе,
(dfrac{5}{100}x) грамм – масса кислорода во втором газе,
тогда масса кислорода в третьем газе составляет (dfrac{14,6}{100}(2x + 300)) грамм.
Так как третий газ возник в результате смешивания первого и второго, то:
[dfrac{21}{100}(x + 300) + dfrac{5}{100}x = dfrac{14,6}{100}(2x + 300),] откуда находим (x = 600). Таким образом, масса третьего газа равна (600 + 600 + 300 = 1500) грамм.
Ответ: 1500
Задание
3
#843
Уровень задания: Равен ЕГЭ
Иван случайно смешал молоко жирностью (2,5%) и молоко жирностью (6%). В итоге у него получилось 5 литров молока жирностью (4,6%). Сколько литров молока жирностью (2,5%) было у Ивана до смешивания?
Пусть (x) литров молока жирностью (2,5%) было у Ивана, тогда
(5 – x) литров молока жирностью (6%) было у Ивана,
(dfrac{2,5}{100}x) – объём жира в молоке жирностью (2,5%), (dfrac{6}{100}(5 – x)) – объём жира в молоке жирностью (6%).
Так как в итоге жира оказалось (dfrac{4,6}{100} cdot 5 = 0,23) литра, то:
(dfrac{2,5}{100}x + dfrac{6}{100}(5 – x) = 0,23), откуда находим (x = 2).
Ответ: 2
Задание
4
#841
Уровень задания: Равен ЕГЭ
В сосуде А содержится 3 литра 17-процентного водного раствора вещества Х. Из сосуда В в сосуд А перелили 7 литров 19-процентного водного раствора вещества Х. Сколько процентов составляет концентрация полученного в сосуде А раствора?
Концентрация в процентах – это отношение объёма вещества к объёму смеси, умноженное на 100(%). До переливания в сосуде А было (3 cdot 0,17 = 0,51) литра вещества Х, в сосуде В было (7 cdot 0,19 = 1,33) литра вещества Х.
После переливания объём вещества Х в сосуде А стал (0,51 + 1,33 = 1,84) литра, а объём всего раствора (3 + 7 = 10) литров. Тогда концентрация в процентах составила [dfrac{1,84}{10} cdot 100% = 18,4%.]
Ответ: 18,4
Задание
5
#2133
Уровень задания: Равен ЕГЭ
Во сколько раз больше должен быть объём (5)-процентного раствора кислоты, чем объём (10)-процентного раствора той же кислоты, чтобы при смешивании получить (7)-процентный раствор?
Пусть объём (5)-процентного раствора кислоты равен (x) литров, а объём (10)-процентного раствора равен (y) литров, тогда требуется найти значение величины (dfrac{x}{y}) при условии [0,05x + 0,1y = 0,07(x + y)
qquadLeftrightarrowqquad
dfrac{x}{y} = dfrac{3}{2} = 1,5,,] таким образом, ответ: (1,5).
Ответ: 1,5
Задание
6
#2134
Уровень задания: Равен ЕГЭ
Во сколько раз больше должен быть объём (20)-процентного раствора кислоты, чем объём (14)-процентного раствора той же кислоты, чтобы при смешивании получить (18)-процентный раствор?
Пусть объём (20)-процентного раствора кислоты равен (x) литров, а объём (14)-процентного раствора равен (y) литров, тогда требуется найти значение величины (dfrac{x}{y}) при условии [0,2x + 0,14y = 0,18(x + y)
qquadLeftrightarrowqquad
dfrac{x}{y} = 2,,] таким образом, ответ: (2).
Ответ: 2
Задание
7
#2629
Уровень задания: Равен ЕГЭ
Смешав (25)-процентный и (95)-процентный растворы кислоты и добавив (20) кг чистой воды, получили (40)-процентный раствор кислоты. Если бы вместо (20) кг воды добавили (20) кг (30)-процентного раствора той же кислоты, то получили бы (50)-процентный раствор кислоты. Сколько килограммов (25)-процентного раствора использовали для получения смеси?
Заметим, что вода – это раствор, не содержащий кислоту, то есть содержащий (0%) кислоты.
Пусть (x) кг – масса раствора с (25)-процентным содержанием кислоты, (y) кг – масса раствора с (95)-процентным содержанием кислоты. Составим схему, описывающую получение (40)-процентного раствора:
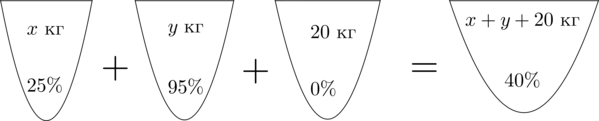
Заметим, что количество кислоты во всех трех растворах равно количеству кислоты в получившемся растворе. Найдем количество кислоты в первом растворе.
Если раствор весит (x) кг, а в нем (25%) кислоты, то в килограммах в нем (dfrac{25}{100}cdot x) кислоты.
Таким же образом можно посчитать количество кислоты в остальных растворах. Получим первое уравнение:
[dfrac{25}{100}cdot x+dfrac{95}{100}cdot y+
dfrac{0}{100}cdot 20=dfrac{40}{100}cdot (x+y+20)]
Аналогично составим схему, описывающую получение (50)-процентного раствора:
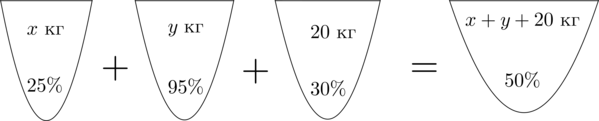
Значит, уравнение, описывающее эту ситуацию, будет выглядеть так:
[dfrac{25}{100}cdot x+dfrac{95}{100}cdot y+
dfrac{30}{100}cdot 20=dfrac{50}{100}cdot (x+y+20)]
Таким образом, решив систему из полученных двух уравнений, найдем (x). Для этого можно умножить оба уравнения на (100), чтобы сделать их проще на вид:
[begin{cases}
25x+95y+0=40(x+y+20)\
25x+95y+30cdot 20=50(x+y+20)
end{cases}]
Вычтем из второго уравнения первое и получим новую систему:
[begin{aligned} &begin{cases}
25x+95y=40(x+y+20)\
30cdot 20=10(x+y+20)
end{cases} quad Rightarrow quad begin{cases}
5x+19y=8(x+y+20)\
y=40-x end{cases} quad Rightarrow \[2ex] Rightarrow quad
&begin{cases}
3x-11(40-x)+160=0\
y=40-x end{cases} quad Rightarrow quad begin{cases}
x=20\y=20end{cases} end{aligned}]
Таким образом, раствора с (25%) кислоты было (20) кг.
Ответ: 20
Источник
Задачи на сплавы, смеси, растворы встречаются и в математике, и в химии. У химиков сложнее – там вещества еще и взаимодействуют, превращаясь во что-то новое. А в задачах по математике мы просто смешиваем растворы различной концентрации. Покажем правила решения на примере задач на растворы. Для сплавов и смесей – действуем аналогично.
. В сосуд, содержащий литров -процентного водного раствора некоторого вещества, добавили литров воды. Сколько процентов составляет концентрация получившегося раствора?
В решении подобных задач помогает картинка. Изобразим сосуд с раствором схематично — так, как будто вещество и вода в нем не перемешаны между собой, а отделены друг от друга, как в коктейле. И подпишем, сколько литров содержат сосуды и сколько в них процентов вещества. Концентрацию получившегося раствора обозначим .

Первый сосуд содержал литра вещества. Во втором сосуде была только вода. Значит, в третьем сосуде столько же литров вещества, сколько и в первом:
.
. Смешали некоторое количество -процентного раствора некоторого вещества с таким же количеством -процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
Пусть масса первого раствора равна . Масса второго — тоже . В результате получили раствор массой . Рисуем картинку.

Получаем:
Ответ: .
. Виноград содержит влаги, а изюм — . Сколько килограммов винограда требуется для получения килограммов изюма?
Внимание! Если вам встретилась задача «о продуктах», то есть такая, где из винограда получается изюм, из абрикосов урюк, из хлеба сухари или из молока творог — знайте, что на самом деле это задача на растворы. Виноград мы тоже можем условно изобразить как раствор. В нем есть вода и «сухое вещество». У «сухого вещества» сложный химический состав, а по его вкусу, цвету и запаху мы могли бы понять, что это именно виноград, а не картошка. Изюм получается, когда из винограда испаряется вода. При этом количество «сухого вещества» остается постоянным. В винограде содержалось воды, значит, «сухого вещества» было . В изюме воды и «сухого вещества». Пусть из кг винограда получилось кг изюма. Тогда
от от
Составим уравнение:
и найдем .
Ответ: .
. Имеется два сплава. Первый сплав содержит никеля, второй — никеля. Из этих двух сплавов получили третий сплав массой кг, содержащий никеля. На сколько килограммов масса первого сплава меньше массы второго?
Пусть масса первого сплава равна x, а масса второго равна y. В результате получили сплав массой .

Запишем простую систему уравнений:
Первое уравнение — масса получившегося сплава, второе — масса никеля.
Решая, получим, что .
Ответ: .
. Смешав -процентный и -процентный растворы кислоты и добавив кг чистой воды, получили -процентный раствор кислоты. Если бы вместо кг воды добавили кг -процентного раствора той же кислоты, то получили бы -процентный раствор кислоты. Сколько килограммов -процентного раствора использовали для получения смеси?
Пусть масса первого раствора , масса второго равна . Масса получившегося раствора равна . Запишем два уравнения, для количества кислоты.
Решаем получившуюся систему. Сразу умножим обе части уравнений на , поскольку с целыми коэффициентами удобнее работать, чем с дробными. Раскроем скобки.
Ответ: .
Источник
Задачи на процентное соотношение в растворах, смесях, сплавах.
Учитель: Коряковцева Н.В.
Блок задач для подготовки к ЕГЭ.
Рассматриваю несколько задач, которые можно решить несколькими способами.
В сосуд, содержaщий 5 литров 12 пpоцентного водного рaствоpa некоторого вещества, добaвили 7 литров воды. Сколько пpоцентов составляет концентpaция получившегося paствоpa?
1.Аpифметический способ.
Представим, что раствор отстоялся.
объем получившегося paствоpa
объем чистого вещества в первом paствоpе.
концентpaция получившегося paствоpa.
2. По формуле.
где концентрация первого и второго растворов соответственно.
объемы первого и второго растворов соответственно
3. С использованием пропорциональности.
Объем раствора увеличился в 2,4 раза (было 5 л., стало 12 л. 12:5 = 2,4),
содержание вещества не изменилось, поэтому процентная концентрация получившегося раствора уменьшилась в 2,4 раза.12:2,4=5(%)
Ответ: 5 %.
2
Сколько литров воды нужно добавить в 2 л водного раствора, содержащего 60% кислоты, чтобы получить 20 процентный раствор кислоты?
Объем чистой кислоты в растворе не меняется, процентное содержание кислоты в растворе уменьшится в 3 раза (60:20=3)
Объем раствора увеличится в 3раза:2·3=6(л)
6 – 2 = 4 (л) воды нужно добавить.
Ответ: 4 л.
3
Смешали 4 литра 15 процентного водного раствора с 6 литрами 25 процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
1. По формуле.
где концентрация первого и второго растворов соответственно.
объемы первого и второго растворов соответственно.
2.Арифметический способ
объем получившегося раствора.
объем чистого вещества в четырех литрах раствора.
объем чистого вещества в шести литрах раствора.
объем чистого вещества в получившемся растворе.
концентрация получившегося раствора.
Ответ: 21%
4
Влажность сухой цементной смеси на складе составляет 18%. Во время перевозки из-за дождей влажность смеси повысилась на 2%. Найдите массу привезенной смеси, если со склада было отправлено 400 кг.
воды в цементе на складе.
сухого вещества в цементе на складе.
сухого вещества в цементе в 328 килограммах.
масса привезенной смеси.
Ответ: 410 кг.
5
Сколько надо взять 5 процентного и 25 процентного раствора кислоты, чтобы получить 4 л 10 процентного раствора кислоты?
0,1· 4=0,4(л) – кислоты в новом растворе.
Пусть х л надо взять первого раствора. Тогда второго – (4 – х) л, а количество получившегося раствора 2х.
0,05х л – кислоты в первом растворе.
0,25· (4 – х) л – кислоты во втором растворе.
0,05х + 0,25· (4 – х) = 0.05х + 1 – 0,25х = (1 – 0,2х) л.
Получим уравнение
3 л надо взять первого раствора.
4 – 3 = 1 л – второго.
Ответ: 1 л, 3 л.
6
В сосуд емкостью 6л налито 4л 70% раствора серной
кислоты. Во второй сосуд той же емкости налито 3л 90% раствора серной кислоты. Сколько литров раствора нужно перелить из второго сосуда в первый, чтобы в нем получился 74% раствор серной кислоты? Найдите все допустимые значения процентного содержания раствора серной кислоты в 6л раствора в первом сосуде.
Пусть х литров раствора кислоты нужно перелить из второго сосуда в первый. Тогда в нем станет (4 + х) литров 74 процентного раствора.
кислоты в первом сосуде.
(0,9х) литров – кислоты нужно перелить.
(2,8 + 0,9х) литров – кислоты в новом растворе.
Учитывая, что новый раствор 74% и его объем (4 + х) литров, то кислоты в нем (0,74·(4 + х )) литров.
Получим уравнение:
Найдем допустимые значения процентного содержания.
Так как в первый сосуд налит 70 процентный раствор серной кислоты, а будем доливать 90 процентный раствор, то процентное содержание раствора будет увеличиваться.
Из второго сосуда в первый можно перелить максимальное количество раствора кислоты – 2 литра.
кислоты в двух литрах.
кислоты будет в первом сосуде.
Тогда процентное содержание раствора серной кислоты в шести литрах раствора в первом сосуде может быть
Ответ: 1;
7
Первый сплав содержит 10% меди, второй – 40% меди. Масса второго сплава больше массы первого на 3кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Пусть х кг масса первого сплава. Тогда масса второго сплава (х + 3) кг, а масса третьего сплава (х + (х + 3)) = (2х + 3) кг.
Масса меди в первом сплаве (0,1х) кг, во втором – (0,4·(х + 3)) кг, а в третьем – (0,3· (2х +3)) кг.
Получим уравнение:
3 кг масса первого сплава.
2 · 3 + 3 = 9 (кг) – масса третьего сплава.
Ответ: 9 кг.
8
Имеется два сплава золота и серебра: в одном массы этих металлов находятся в отношении 2:3, а в другом – в
отношении 3:7. Сколько килограммов нужно взять от каждого сплава, чтобы получить 8 кг нового сплава, в котором золото и серебро находились бы в отношении 5:11?
Пусть х кг масса куска, взятого от первого сплава. Тогда масса куска, взятого от второго сплава (8 – х) кг.
Масса золота в первом куске
Масса золота во втором куске
Масса золота в новом сплаве
Получим уравнение
1 кг нужно взять от первого сплава.
8 – 1 = 7 (кг) – от второго сплава.
Ответ: 1кг; 7 кг.
В этой задаче можно было бы составить и другие уравнения
*
*
*
9
Имеется два сплава. Первый содержит 10% никеля, второй- 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго?
Пусть х кг масса первого сплава, у кг – второго.
Так как масса третьего сплава 200 кг, то получим уравнение
Масса никеля в первом сплаве (0,1х) кг, во втором – (0,3у) кг, а в новом – 200·0,25=50 кг. Получим второе уравнение
Получим систему уравнений:
50 кг – масса первого сплава.
150 кг – масса второго сплава.
150 – 50 = 100 (кг)
Ответ: на 100 кг.
10
При смешивании 30 процентного раствора серной кислоты с10 процентным раствором серной кислоты получилось 400 г 15 процентного раствора. Сколько граммов 30 процентного раствора было взято?
Пусть х г масса 30 процентного раствора серной кислоты, а у г – 10 процентного. Получим уравнение х + у = 400.
кислоты в новом растворе.
кислоты в первом растворе.
кислоты во втором растворе.
Получим второе уравнение
Получим систему уравнений:
100 г 30 процентного раствора было взято.
Ответ:100 г.
Задачи для тренировки.
1.К 10 литрам 45%-ного водного раствора кислоты добавили некоторое количество чистой воды, в результате чего концентрация кислоты в растворе снизилась до 37,5%. Сколько литров воды было добавлено?
Ответ: 2
2.К 9 литрам водного раствора кислоты добавили 3 литра чистой воды.
Смесь тщательно перемешали, а затем 3 литра раствора отлили. Эту процедуру выполнили еще 2 раза, после чего получили 9 литров 27%-ного раствора кислоты. Какова была исходная концентрация кислоты в растворе?
Ответ 6
3.К 8 литрам водного раствора кислоты добавили 4 литра 27-процентного раствора той же кислоты. Смесь тщательно перемешали, а затем такое же количество, т.е. 4 литра, отлили. Операцию повторили трижды, после чего концентрация кислоты составила 43%. Какова была исходная концентрация кислоты в растворе?
Ответ: 81
4.Из сосуда, доверху наполненного 97%-м раствором кислоты, отлили 2 литра жидкости и долили 2 литра 45%-го раствора этой же кислоты. После этого в сосуде получился 81%-й раствор кислоты. Сколько литров раствора вмещает сосуд?
Ответ:6,5
5.Из сосуда, доверху наполненного 93%-м раствором кислоты, отлили 1,5 литра жидкости и долили 1,5 литра 69%-го раствора этой же кислоты. После этого в сосуде получился 85%-й раствор кислоты. Сколько литров раствора вмещает сосуд?
Ответ:4,5
6.Из сосуда, доверху наполненного 99%-м раствором кислоты, отлили 3,5 литра жидкости и долили 3,5 литра 51%-го раствора этой же кислоты. После этого в сосуде получился 89%-й раствор кислоты. Сколько литров раствора вмещает сосуд?
Ответ:16,8
7.В бидон налили 7 литров трёхпроцентной жирности и 3 литра молока шестипроцентной жирности. Какова жирность полученного молока?
Ответ: 3,9
8.В бидон налили 4 литра молока трёхпроцентной жирности и 6 литров молока шестипроцентной жирности. Какова жирность полученного молока в бидоне?
Ответ: 4,8
9.В бидон налили 3 литра молока трёхпроцентной жирности и 7 литров молока шестипроцентной жирности. Какова жирность полученного молока (в процентах)?
Ответ: 5,1
10.В бидон налили 9 литров трёхпроцентной жирности и 1 литр молока шестипроцентной жирности. Какова жирность полученного молока(в процентах)?
Ответ: 3,3
11.Сплав алюминия и магния отличается большой прочностью и пластичностью. Взяли два таких сплава, сплавили их и получили сплав, содержащий 4% магния. Отношение масс первого и второго сплавов равно 3:2. Определите процент содержания магния во втором сплаве, если первый сплав содержит 6% магния?
Ответ: 1
12.Смешали 160г раствора, содержащего 60% соли, и 240г раствора, содержащего 40% соли. Сколько процентов соли в получившемся растворе?
Ответ: 48
13.Влажность сухой цементной смеси на складе составляет 18%. Во время перевозки из-за дождей влажность смеси повысилась на 2%. Найдите массу привезённой смеси, если со склада отправлено 400кг.
Ответ: 410
14.Кусок сплава меди и цинка в 36кг содержит 45% меди. Какую массу меди нужно добавить к этому куску, чтобы полученный новый сплав содержал 60% меди?
Ответ: 13,5
15.Сколько кг воды надо добавить к 18% раствору соли массой 8кг, чтобы получить новый раствор с содержанием 16%?
Ответ: 1
16.Собрали 140кг грибов, влажность которых составила 98%. После первоначального подсушивания их влажность снизилась до 93%. Какова стала масса грибов после подсушивания?
Ответ: 40
17.Сколько литров воды надо добавить к 0,3л 70% раствора уксусной эссенции, чтобы получился 3% уксусный раствор?
Ответ: 6,7
18.В сосуд ёмкостью 6л налито 4л 70% раствора серной кислоты. Во второй сосуд той же ёмкости налито 3л 90%-ного раствора серной кислоты. Сколько литров раствора нужно перелить из второго сосуда в первый, чтобы в нём получился 74% раствор серной кислоты? Найдите все допустимые значения процентного содержания раствора серной кислоты в 6 литрах раствора в первом сосуде?
Ответ: 1;
19.Если смешать 8кг и 2кг растворов серной кислоты разной концентрации, то получим 12-ти процентный раствор кислоты. При смешивании двух одинаковых масс тех же растворов получим 15-ти процентный раствор. Определите первоначальную концентрацию каждого раствора.
Ответ: 10 и 20
20.Имеются два слитка золота и серебра. В первом отношении золота и серебра равно 1:2, во втором 2:3. Если сплавить 1/3 первого слитка и 5/6 второго, то в полученном слитке будет столько золота, сколько в первом было серебра. Если же 2/3 первого слитка сплавить с половиной второго, то в получившемся слитке серебра будет на 1кг больше, чем было золота во втором слитке. Сколько золота в каждом слитке?
Ответ: 1,2 и 2,4
21.Свежие грибы содержат по весу 90% воды, а сухие – 12% воды. Сколько получится сухих грибов из 22кг свежих грибов?
Ответ: 2,5
22.На складе было 100кг ягод. Анализ показал, что в ягодах 99% воды. Через некоторое время содержание воды в ягодах упало до 98%. Сколько стали весить ягоды?
Ответ: 50
23.Сплав меди и цинка весом в 24кг при погружении в воду потерял в весе кг. Определите количество меди и цинка в этом сплаве, если известно, что медь теряет в воде % веса, а цинк – %.
Ответ: 17 и 7
Самостоятельная работа по теме «Задачи на растворы»
Смешали 160г раствора, содержащего 60% соли, и 240г раствора, содержащего 40% соли. Сколько процентов соли в получившемся растворе?
Сколько кг воды надо добавить к 18% раствору соли массой 8кг, чтобы получить новый раствор с содержанием 16%?
Источник
