Задачи на сосуды с поршнями
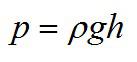
В последнее время мы разбирали решения многих простейших физических задач по разным темам: законы Ньютона, сила трения, свободное падение и т.д. Пришла пора взяться за что-то посложнее. Сегодня решаем задачи по теме «гидростатика».
За полезными лайфхаками и новостями студенческой жизни добро пожаловать на наш телеграм-канал.
Задачи по гидростатике с решениями
Задача №1 на гидростатику
Условие
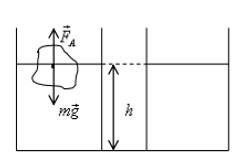
B кувшине с водой плавает кусок льда. Как изменится уровень воды в сосуде, когда лед растает?
Решение
По условию плавания тел:
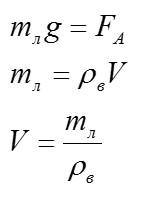
V – объем погруженной в воду части льда. После таяния льда образуется объем воды:
Как видим, объемы совпадают. Это значит, что при таянии льда его объем будет заменен таким же объемом воды.
Ответ: уровень не изменится.
Задача №2 на гидростатику
Условие
Кочан капусты массой 8 кг и объемом 10 л опускают в воду. Какой объем кочана окажется над водой?
Решение
Кочан плавает на поверхности, на него действуют сила Архимеда и сила тяжести:
Здесь V – объем кочана, погруженный в воду. Чтобы узнать объем кочана над водой, нужно из общего объема вычесть погруженный:
В одном кубическом метре – тысяча литров.
Ответ: 2 литра.
Задача №3 на гидростатику
Условие
Каково давление на дне озера глубиной 5 м? Атмосферное давление принять равным 100 кПа.
Решение
Вспоминаем основное уравнение гидростатики и записываем:
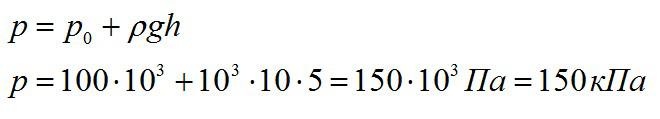
Ответ: 150 кПа.
Задача №4 на гидростатику
Условие
Вес тела в вакууме 2,6Н, в воде 1,6Н. Плотность воды 1000кг/м3. Определите плотность тела.
Решение
Вес – сила, с которой тело действует на опору. В воде вес меньше, так как на тело действует сила Архимеда, которая стремиться «поднять» его. В вакууме вес тела равен силе тяжести.
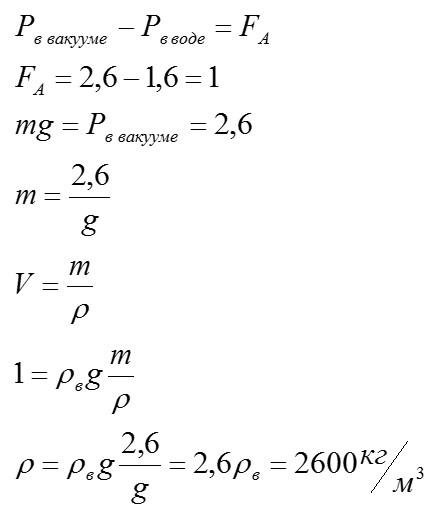
Ответ: 2600 кг/м3.
Задача №5 на гидростатику
Условие
Гидростатическое давление жидкости увеличилось в 5 раз. Как при этом изменилась высота столба жидкости в сосуде?
Решение
Формула для гидростатического давления:
Так как плотность жидкости и ускорение свободного падения остаются неизменными, можно сделать вывод, что высота столба жидкости увеличилась в пять раз.
Ответ: высота увеличилась в 5 раз.
Кстати! Для наших читателей действует скидка 10% на любой вид работы.
Вопросы по гидростатике
Вопрос 1. Что такое гидростатический парадокс?
Ответ. Гидростатический парадокс – явление, когда вес жидкости в сосуде не совпадает с весовым давлением, которое она оказывает на стенки сосуда. Возникает в сосудах конусообразной формы.
Вопрос 2. Какие есть внесистемные единицы изменения давления:
Ответ. Внесистемные единицы давления:
- миллиметр ртутного столба;
- бар;
- атмосфера.
Вопрос 3. В условиях физических задач часто можно встретить формулировку «нормальные условия». Что этот значить?
Ответ. Это значит, что давление нужно брать равным 101325 Па (или 760 мм рт. ст.), а температуру – 0 градусов Цельсия (или 273 Кельвина).
Вопрос 4. Что такое сообщающиеся сосуды?
Ответ. Сообщающиеся сосуды – это емкости, соединенные между собой. Жидкость может свободно перетекать из одного сосуда в другой. Уровень жидкости с одной плотностью в сообщающихся сосудах всегда одинаков. Простейший пример сообщающихся сосудов: обычный чайник. Если мы нальем в него воду, уровень будет одинаковым как в носике, так и в основном объеме. Если же плотности жидкостей разные, то выше будет уровень той, у которой плотность меньше.
Вопрос 5. Что такое гидравлический пресс?
Ответ. Гидравлический пресс – устройство, в основе действия которого лежит закон Паскаля и принцип сообщающихся сосудов. Пресс состоит из двух соединённых и заполненных маслом цилиндров: узкого и широкого. При нажатии на поршень узкого цилиндра, широкий цилиндр получает во столько раз большее давление, во сколько раз площадь большего поршня больше площади меньшего поршня.
Гидростатика: немного теории
Гидростатика – раздел физики, изучающий равновесие жидкостей.
Равновесие жидкостей – очень важный раздел. Например, если вы выпили много пива, просто необходимо, чтобы оно находилось в равновесии. Но шутки в сторону! Какие фундаментальные понятия нужно знать, чтобы решать задачи по гидростатике?
Давление и плотность
Давление – физическая величина, равная отношению модуля силы, перпендикулярно действующей на поверхность, к площади этой поверхности.
Давление столба жидкости называют гидростатическим, а измеряется оно в Паскалях. Гидростатическое давление столба жидкости высотой h на дно сосуда рассчитывается по формуле:
Греческое «ро» – плотность жидкости. Плотность измеряется в килограммах на кубический метр и равна отношению массы тела к его объему.
Жидкость – изотропная среда. Это значит, что ее свойства одинаковы в любой ее точке.
Закон Паскаля и основное уравнение гидростатики
Давление, оказываемое на жидкость или газ передается в любую точку этой жидкости одинаково и во всех направлениях.
Это и есть закон Паскаля. Согласно ему, давление жидкости зависит только от плотности жидкости и высоты ее столба. На глубине h жидкость оказывает одинаковое давление как на дно, так и на стенки сосуда.
В данном случае р нулевое – давление столба воздуха (атмосферы), которое действует на жидкость.
В своей другой формулировке основное уравнение гидростатики показывает, что гидростатический напор является постоянной величиной для всего объема неподвижной жидкости. Здесь мы не будем останавливаться на этом понятии, так как оно изучается в курсе гидравлики.
Закон Архимеда и условия плавания тел
Закон Архимеда – еще одна важнейшая часть гидростатики. Он гласит:
На тело, погруженное в газ или жидкость действует выталкивающая сила, равная весу жидкости (газа) в объеме погруженной части тела. Эта сила называется силой Архимеда.
Тело плавает, если выталкивающая сила Архимеда больше действующей на него силы тяжести. Это же условие можно переписать, используя понятие плотности: тело будет плавать, если плотность жидкости больше, чем плотность тела.
Подробнее о законе Архимеда и фактах из жизни этого выдающегося античного инженера читайте в нашем отдельном материале.
Нужна помощь в решении задач? Обращайтесь в профессиональный студенческий сервис за качественным и быстрым объяснением.
Источник
>>> Перейти на мобильный размер сайта >>>
Учебник для 10 класса
ФИЗИКА
Задачи на применение газовых законов очень разнообразны. Для их решения нельзя указать какой-либо один определенный прием. Полезными могут оказаться следующие советы.
- Если согласно условию задачи один из трех параметров (р, V или Т) постоянный, то при Т = const надо применять закон Бойля—Мариотта (3.5.2), при р = const — закон Гей-Люссака (3.7.7), а при V = const — закон Шарля (3.10.2) или (3.10.3).
- Если изменяются все три параметра, то следует воспользоваться уравнением состояния в форме (3.9.9) или (3.9.5).
Уравнение состояния (3.9.9) применяется в тех случаях, когда известна масса газа и часть макроскопических параметров в определенном состоянии газа и надо найти неизвестные величины.
- Для определения давления смеси газов, не вступающих в химические реакции, используют закон Дальтона (3.8.2).
- Во многих задачах требуется построение графиков, изображающих разного рода процессы. Для этого нужно знать зависимость параметров друг от друга, которая в общем случае дается уравнением состояния, а в частных — газовыми законами.
- При решении большинства задач надо четко представлять себе, каково начальное состояние системы и какой процесс переводит его в конечное состояние.
Задача 1
Как измерить медицинским термометром температуру тела человека, если температура окружающего воздуха +42 °С?
Решение. Можно предварительно охладить термометр в холодильнике. Если холодильника нет, то нужно подержать термометр 5—8 мин под мышкой, извлечь его и сразу же стряхнуть. Термометр покажет температуру тела, так как ртуть в термометре сожмется при контакте с телом до объема, соответствующего температуре тела.
Задача 2
Газ в цилиндрическом сосуде разделен на две равные части подвижным поршнем, имеющим массу m и площадь сечения S. При горизонтальном положении цилиндра давление газа в каждой половине сосуда равно р. Определите давление р1 газа над поршнем при вертикальном положении цилиндра. Температуру газа считать постоянной.
Решение. При горизонтальном положении цилиндра объем каждой его части обозначим через V (эти объемы равны). При вертикальном положении цилиндра объем верхней части станет равным V + ΔV, а нижней V – ΔV. Давление в нижней части цилиндра станет равным . Согласно закону Бойля— Мариотта
Исключив из этих равенств , получим квадратное уравнение для p1:
Отсюда
Второй корень квадратного уравнения отрицателен и потому лишен физического смысла.
Задача 3
Поршневой насос при каждом качании захватывает воздух объемом V0. При откачке этим насосом воздуха из сосуда объемом V насос совершил п качаний. Затем другой насос с тем же рабочим объемом V0 начал нагнетать воздух из атмосферы в тот же сосуд, совершив также п качаний. Какое давление установится в сосуде? Температуру воздуха во время работы насоса считать постоянной.
Решение. Согласно закону Бойля—Мариотта при откачке воздуха из сосуда после первого качания давление в сосуде станет равным , где p0— атмосферное давление.
После второго качания будет выполняться равенство p1V = p2(V + V0) и, следовательно, и т.д. После n качаний в сосуде установится давление
При нагнетании воздуха в сосуд после n качаний давление станет равным
При любом n р > р0, так как во время нагнетания воздуха при каждом качании насос захватывает воздух, имеющий атмосферное давление р0, а при откачке при каждом качании удаляется воздух при давлении, меньшем р0.
Задача 4
В запаянной с обоих концов цилиндрической трубке находится воздух при нормальных условиях. Трубка разделена подвижным поршнем на две части, объемы которых V1 и V2 относятся как 1 : 2. До какой температуры t1 следует нагреть воздух в меньшей части трубки и до какой t2 охладить в большей, чтобы поршень делил трубку на две равные части, если нагревание и охлаждение в обеих частях трубки производятся при условии = const?
Решение. Условие = const означает, что процессы нагревания и охлаждения происходят изобарно. При отношении начальных объемов эти объемы составляют и , где V0 — объем всей трубки. Конечные объемы обеих частей одинаковы и равны .
Согласно закону Гей-Люссака для воздуха в меньшей части трубки выполняется соотношение
а для воздуха в большей части
где Т0 = 273 К — температура, соответствующая начальным условиям. Отсюда
Задача 5
В цилиндре под поршнем находится воздух при давлении p1 = 2 • 105 Па и температуре t1 = 27 °С. Определите массу m груза, который нужно положить на поршень после нагревания воздуха до температуры t2 = 50 °С, чтобы объем воздуха в цилиндре стал равен первоначальному. Площадь поршня S = 30 см2.
Решение. Так как в процессе нагревания объем воздуха в цилиндре не изменяется, то согласно закону Шарля имеем
где
Подставляя в (3.12.1) выражение для р2, получим
Отсюда
Задача 6
Найдите среднюю (эффективную) молярную массу сухого атмосферного воздуха, предполагая известный процентный состав воздуха по массе: азот — n1 = 75,52%, кислород — n2 = 23,15%, аргон — n3 = 1,28% и углекислый газ — n4 = 0,05%.
Решение. Для каждого газа можно записать уравнение состояния:
Здесь M1, M2, M3 и M4 — молярные массы соответственно азота, кислорода, аргона и углекислого газа.
Складывая правые и левые части этих уравнений, получим
Для смеси газов выполняется соотношение
где m = m1 + m2 + m3 + m4 — масса воздуха с объемом V, а М — искомая эффективная молярная масса. Согласно закону Дальтона
p = p1 + p2 + p3 + p4.
Сравнивая уравнения состояния (3.12.2) и (3.12.3), получим
Разделив числитель и знаменатель на m и умножив на 100%, получим выражение для М через процентный состав воздуха по массе
Задача 7
Закрытый с обоих концов цилиндр наполнен газом при давлении p = 100 кПа и температуре t = 30 °С и разделен подвижным теплонепроницаемым поршнем на две равные части длиной L по 50 см. На какую величину ΔT нужно повысить температуру газа в одной половине цилиндра, чтобы поршень сместился на расстояние l = 20 см, если во второй половине цилиндра температура не изменяется? Определите давление газа после смещения поршня.
Решение. Для газа в части цилиндра с постоянной температурой применим закон Бойля—Мариотта:
где S — площадь основания цилиндра. Для нагреваемой части цилиндра запишем уравнение Клапейрона:
В уравнениях (3.12.4) и (3.12.5) р1 — давление газа после смещения поршня, одинаковое в обеих частях цилиндра вследствие равновесия поршня, а Т + ΔT в уравнении (3.12.5) — температура газа в нагретой части цилиндра.
Разделив почленно уравнение (3.12.4) на уравнение (3.12.5), получим
Отсюда
Из уравнения (3.12.4) находим p1:
Задача 8
Сосуд объемом V = 100 л разделен пополам полупроницаемой перегородкой. В начальный момент времени в одной половине сосуда находился водород, масса которого m1 = 2 г, а во второй — 1 моль азота. Определите давления, установившиеся по обе стороны перегородки, если она может пропускать только водород. Температура в обеих половинах одинакова и постоянна: t = 127 °С.
Решение. Так как водород свободно проходит через перегородку, то он распространяется по всему сосуду. Запишем уравнение Менделеева—Клапейрона для водорода после установления состояния равновесия:
где М1 = 2 • 10-3 кг/моль — молярная масса водорода.
В той части сосуда, в которой вначале был только водород, он и в дальнейшем останется в чистом виде, так что давление в этой части сосуда станет равным
Для азота уравнение Менделеева—Клапейрона имеет вид
где р2 — давление азота.
Так как в этой половине находятся водород и азот, то полное давление р согласно закону Дальтона складывается из парциальных давлений р1 и р2, т. е.
Задача 9
Гелий массой 20 г, заключенный в теплоизолированном цилиндре под поршнем, медленно переводится из состояния 1 с объемом V1 = 32 л и давлением р1 = 4,1 атм в состояние 2 с объемом V2 = 9 л и давлением р2 = 15,5 атм. Какой наибольшей температуры достигнет газ при этом процессе, если на графике зависимости давления газа от объема процесс изображается прямой линией (рис. 3.18)?

Рис. 3.18
Решение. Как следует из рисунка 3.18, давление и объем газа связаны линейной зависимостью: р = aV + b, где а и b — постоянные коэффициенты. Из условий задачи получаем систему уравнений
Решив эту систему относительно а и b, найдем
Подставив в уравнение Менделеева—Клапейрона вместо р выражение aV + b, получим
График зависимости Т от V представляет собой параболу (рис. 3.19).

Рис. 3.19
Кривая достигает максимума при Vmax = = 20 л, когда корни квадратного уравнения (3.12.6) совпадают. При этом
Следовательно,
Задача 10
На рисунке 3.20 изображен график изменения состояния идеального газа в координатах р, V. Начертите графики этого процесса в координатах V, Т и р, Т.

Рис. 3.20
Решение. Из рисунка 3.20 следует, что давление газа р и его объем V находятся в прямой пропорциональной зависимости
где k — постоянный коэффициент. Подставив значение давления (3.12.7) в уравнение Менделеева— Клапейрона, получим
или
Уравнение (3.12.8) — это уравнение параболы, ось симметрии которой совпадает с осью Т. Следовательно, в координатах V, Т искомый график имеет вид, показанный на рисунке 3.21, а. Аналогично получим график этого процесса в координатах p, T (рис. 3.21, б).

Рис. 3.21
Упражнение 2
- Вы надули щеки. При этом и давление, и объем воздуха во рту увеличиваются. Как это согласуется с законом Бойля— Мариотта?
- Чтобы измерить температуру человеческого тела, приходится держать термометр под мышкой в течение 5—8 мин. В то же время стряхнуть его можно практически сразу после измерения температуры. Почему?
- Узкая вертикальная трубка длиной L, закрытая с одного конца, содержит воздух, отделенный от наружного воздуха столбиком ртути длиной h. Плотность ртути равна ρ. Трубка расположена открытым концом вверх. Какова была длина l столбика воздуха в трубке, если при перевертывании трубки открытым концом вниз из трубки вылилась половина ртути? Атмосферное давление равно р0.
- В ртутный барометр попал пузырек воздуха, вследствие чего барометр показывает давление меньше истинного. При давлении р1 = 768 мм рт. ст. уровень ртути расположен на высоте h1 = 748 мм, причем длина пустой части трубки l = 80 мм. Каково атмосферное давление р2, если ртуть стоит на высоте h2 = 734 мм? Плотность ртути ρ = 1,36 • 104 кг/м3.
- Площадь сечения цилиндра автомобильного насоса S = 10 см2. Определите длину l цилиндра, если известно, что для накачки шины объемом V = 0,02 м3 от давления р0 = 1 • 105 Па до давления р = 3 • 105 Па требуется совершить n = 100 качаний. Утечкой и нагреванием воздуха пренебречь.
- В цилиндре под поршнем находится воздух. Поршень имеет форму, показанную на рисунке 3.22. Масса поршня m = 6 кг, площадь сечения цилиндра S = 20 см2. Атмосферное давление р0 = 105 Па. Найдите массу m1 груза, который надо положить на поршень, чтобы объем V1 воздуха в цилиндре уменьшился в 2 раза. Трение не учитывать. Температура постоянна.

Рис. 3.22
- Газ нагрет от температуры t1 = 27 °С до температуры t2 = 39 °С. На сколько процентов увеличился его объем, если давление осталось неизменным?
- Вертикальный цилиндр, закрытый подвижным поршнем, содержит газ массой m — 0,012 кг. При температуре t1 = = 177 °С объем газа равен V1 = 4 л. При какой температуре t2 плотность этого газа будет равна ρ2 = 5,3 кг/м3?
- Открытую стеклянную колбу, имеющую форму шара радиусом r = 2 см с горлышком длиной l = 10 см и диаметром d = 1 см, нагрели до температуры t1, а затем погрузили целиком в воду горлышком вниз. При охлаждении колбы вода вошла в горлышко. Когда температура колбы стала равной t2 = 13 °С, ее начали приподнимать из воды, не переворачивая, так чтобы шарообразная часть оказалась над водой, а горлышко — частично погруженным в воду. При этом, когда уровень воды в горлышке и в сосуде совпал, под водой осталась половина горлышка. Какова была температура t1, до которой нагрели колбу?
- Манометр на баллоне с газом в помещении с температурой t1 = 17 °С показывает давление р = 240 кПа. На улице показание манометра уменьшилось на Δр = 40 кПа. Найдите температуру наружного воздуха, если атмосферное давление р0 = 100 кПа.
- Два сосуда одинаковой вместимости содержат воздух, один при температуре Т1 и давлении р1, другой при температуре T2 и давлении р2. Сосуды соединили тонкой трубкой и после выравнивания давлений и температур воздух нагрели до температуры Т. Какое давление установится после нагревания?
- Шар-зонд заполнен газом при температуре t1 = 27 °С до давления р1 = 105 кПа. После подъема шара на высоту, где давление р0 = 80 кПа, объем шара увеличился на n = 5% и давление в нем стало отличаться от внешнего на Δр = 5 кПа. Определите температуру воздуха на этой высоте, предполагая, что газ в шаре приобрел температуру окружающего воздуха.
- Из баллона со сжатым углекислым газом из-за неисправности вентиля вытекает газ. Вместимость баллона V = 10 л. При температуре Т1 = 263 К манометр показывал давление р1 = 9,3 атм, а через некоторое время при температуре Т2 = 295 К манометр показывал давление р2 = = 9,4 атм. Чему равна масса m газа, вытекшего из баллона за это время?
- Газ последовательно переводится из состояния 1 с температурой T1 в состояние 2 с температурой Т2, а затем в состояние 3 с температурой T3 и возвращается в состояние 1. Определите температуру T3, если процессы изменения состояния происходили так, как это показано на графике (рис. 3.23), а температуры Т1 и Т2 известны.

Рис. 3.23
- В баллоне вместимостью V — 10 л содержится водород при температуре t = 20 °С под давлением р = 107 Па. Какая масса водорода была выпущена из баллона, если при полном сгорании оставшегося газа образовалось m = 50 г воды?
- В баллоне вместимостью V = 10 л находился гелий под давлением р1 = 10 атм при температуре t1 = 27 °С. После того как из баллона был выпущен газ массой m = 10 г, температура в баллоне была понижена до t2 = 17 °С. Определите давление гелия, оставшегося в баллоне.
- Молекулярный водород некоторой массы занимает объем V1 = 1 м3 при температуре Т1 = 250 К и давлении р1 = 2 • 105Па. Какое давление водород будет создавать при температуре T2 = 5000 К и объеме V2 = 10 м3, если при столь высокой температуре молекулы водорода полностью диссоциируют на атомы?
- Два сосуда объемом V1 = 200 см3 и V2 = 100 см3, наполненные кислородом при температуре t = 27 °С под давлением p0 = 760 мм рт. ст., соединены трубкой, внутри которой находится теплоизолирующая пористая перегородка, обеспечивающая одинаковость давлений в сосудах. Затем первый сосуд нагрели до температуры t1 = 100 °С, а второй охладили до температуры t2 — 0 °С. Определите установившееся в системе давление.
- Изобразите на графиках в координатах р, V; р, Т и V, Т изотермический процесс для одного моля газа при Т = Т1 и Т = 2Т1.
- Изобразите на графиках в координатах р, V; р, Т и V, T изобарный процесс: 1) для р =р1 и p = 2p1, если v = 1 моль; 2) для р = р1, если v = 3 моль.
- На рисунке 3.24 показан график изменения состояния идеального газа в координатах р, V. Представьте этот процесс на графиках в координатах V, Ти р, Т.

Рис. 3.24
Источник
