Задачи по его про цилиндрические сосуды

Тип урока: Урок открытия и первичного закрепления знаний.

Цель урока: получить выражение для расчёта давления жидкости на дно и стенки сосуда; проверка качества знаний учащихся при решении задач.

Задачи урока:

• Предметные: углубить и закрепить знания о давлении жидкости.
• Метапредметные: продолжить развивать внимание, память, логическое мышление, умение делать выводы.
• Личностные: способствовать формированию научного мировоззрения, активизировать учебно-познавательную деятельность учащихся, содействовать формированию самостоятельности, воспитанию интереса к предмету.

Оборудование к уроку: компьютер, видеопроектор, интерактивная доска, два стакана с водой, цилиндрические сосуды с основаниями различной площади, деревянный брусок, камень, два одинаковые пластмассовые груза, широкий сосуд, аквариум, удочка, каточки с заданиями, учебник по физике.

Ход урока

1.Организационный момент.

2. Актуализация имеющихся знаний.

Взаимопроверка в парах по вопросам. Слайд 1

1. Чем отличается процесс передачи давления в жидкости и газе от передачи давления твёрдыми телами? (давление твёрдыми телами передаётся в направлении действия силы, в жидкости и газе по всем направлениям одинаково)
2. Сформулируйте закон Паскаля. (давление, производимое на жидкость или газ, передаётся в любую точку без изменений во всех направлениях)
3. Мальчик выдувает мыльные пузыри. Почему они принимают форму шара? (они приобретают форму шара, так как давление в газе, согласно закону Паскаля передаётся одинаково по всем направлениям)
4. От чего зависит давление газа? (от объёма, массы и температуры газа)
5. Для космонавтов пищу изготавливают в полужидком виде и помещают в тюбики с эластичными стенками. Что помогает космонавтам выдавливать пищу из тюбиков? (Закон Паскаля)
6. Почему взрыв снаряда под водой губителен для живущих в воде организмов? (давление взрыва в жидкости, согласно закону Паскаля, передаётся одинаково по всем направлениям, и от этого животные могут погибнуть)
7. Почему пловец, нырнувший на большую глубину, испытывает боль в ушах? (с глубиной давление увеличивается; пловец испытывает боль в ушах, так как вода с большой силой давит на барабанные перепонки)

3. Открытие нового знания. Слайд 2

В три сосуда с одинаковой площадью дна, стоящие на столе, налили воды до одного уровня

1) В каком сосуде масса воды больше? Меньше?

2) Одинаковым ли будет давление воды на дно сосудов?

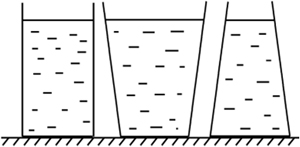
Вы уверены? Как рассчитать давление жидкости на дно сосуда? (Затруднение).

• Какая цель нашего урока? (Узнать, как рассчитать давление жидкости на дно сосуда)
• Какая тема урока? (Расчёт давления жидкости на дно и стенки сосуда) Слайд 3

Учащиеся записывают тему к себе в тетрадь.

Попытаемся вывести формулу для расчёта этого давления. Но какую же форму сосуда нам надо выбрать для расчёта нашей формулы? Я предлагаю взять форму прямоугольного параллелепипеда.

Для того чтобы упростить вывод формулы для расчета давления на дно и стенки сосуда, удобнее всего использовать сосуд в форме прямоугольного параллелепипеда (Рис. 2).

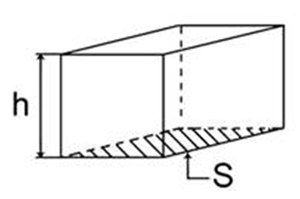
Рис. 2. Сосуд для расчета давления жидкости

Площадь дна этого сосуда – S, его высота – h. Предположим, что сосуд наполнен

жидкостью на всю высоту h. Чтобы определить давление на дно, нужно силу,

действующую на дно, разделить на площадь дна. В нашем случае сила – это вес жидкости P, находящейся в сосуде

Поскольку жидкость в сосуде неподвижна, ее вес равен силе тяжести, которую можно вычислить, если известна масса жидкости m.

P = mg

Напомним, что символом g обозначено ускорение свободного падения.

Для того чтобы найти массу жидкости, необходимо знать ее плотность ρ и объем V

m = ρV

Объем жидкости в сосуде мы получим, умножив площадь дна на высоту сосуда

V = Sh

Эти величины изначально известны. Если их по очереди подставить в приведенные выше формулы, то для вычисления давления получим следующее выражение:

В этом выражении числитель и знаменатель содержат одну и ту же величину S – площадь дна сосуда. Если на нее сократить, получится искомая формула для расчета давления жидкости на дно сосуда:

p = ρgh

Итак, для нахождения давления необходимо умножить плотность жидкости на величину ускорения свободного падения и высоту столба жидкости.

Полученная выше формула называется формулой гидростатического давления. Согласно этой формуле гидростатическое давление не зависит от формы сосуда, в котором находится жидкость и от площади его сечения. Оно зависит от высоты столба жидкости и от плотности жидкости.

Возвратимся к нашему вопросу: Одинаковым ли будет давление воды на дно сосудов? (одинаковым)

Данная формула позволяет найти давление на дно сосуда. А как рассчитать давление на боковые стенки сосуда? Чтобы ответить на этот вопрос, вспомним, что на прошлом уроке мы установили, что давление на одном и том же уровне одинаково во всех направлениях. Это значит, давление в любой точке жидкости на заданной глубине h может быть найдено по той же формуле.

Возвратимся к нашему вопросу: Одинаковым ли будет давление воды на дно сосудов?

4. Физминутка (под медленную, спокойную мелодию)

– Я предлагаю вам, ребята, выполнить дыхательную гимнастику:

1-е упр. Набрать воздух в лёгкие (вдыхаем медленно, но как можно больше воздуха),

Медленно выдохнуть

2-е упр. Руки медленно поднимаем вверх и делаем (одновременно) глубокий вдох.

Руки опускаем – выдох.

3-е упр. Глубоко вдохнуть, садясь за парту, медленно выдыхаем (гимнастика проводится под спокойную музыку).

– Сейчас вы выполнили дыхательную гимнастику, которую врачи рекомендуют проводить 3-4 раза в день.

– А какой физический закон лежит в основе дыхательной гимнастики, как он называется? (в основе дыхательной гимнастики лежит закон Паскаля)

5. Закрепление материала.

 Решение задач.

а) Проведение игры «рыбалка»

Качественные задачи:

1. Куда бы вы перелили сок из литровой банки, чтобы его давление на дно сосуда стало больше: в пятилитровую кастрюлю или в литровую бутылку? (в литровую бутылку)
2. Какие из жидкостей: вода или керосин оказывает меньшее давление на дно сосудов одной формы, если объёмы жидкостей одинаковы? (керосин)
3. Как изменится давление воды на дно доверху наполненного стакана, если в воду опустить камень? (не изменится)
4. В цилиндрический сосуд, частично наполненный водой, опустили деревянный брусок. Как изменится давление воды на дно сосуда? (увечится)
5. Два одинаковых предмета были опущены в цилиндрические сосуды с основаниями различной площади. В цилиндрических сосудах уровень воды до погружения предмета одинаков. В каком сосуде гидростатическое давление больше? (в сосуде меньшей площади)

Ответы на задачи подтверждаются опытами.

б) Расчётные задачи:

1. упр. 17(2)
2. Определите высоту столба керосина, который оказывает давление на дно сосуда равное 8 кПа. Слайд 4

Самостоятельная работа по решению задачи упр.17(1) по рядам?

6. Подведение итогов урока. Рефлексия.

Подведём итоги.

Давайте вспомним, что сегодня делали на уроке, что узнали?

Мне очень важно, с каким настроением вы уходите с урока. Поэтому я прошу вас заполнить лист самоанализа, который находится столах у каждого из вас.

Лист самоанализа (нужное подчеркнуть)

Чувствую вдохновение, подавленность .

Интересно, неинтересно.

Не устал(ла), устал(ла).

Доволен(довольна), недоволен(недовольна).

Вызвало затруднения(перечислить)…

7. Домашнее задание. Слайд 5

п. 40, упр.17(3), задания на с.118