Закон паскаля сообщающиеся сосуды гидравлический пресс
Ещё один фундаментальный закон физики, который изучается в школе и обязателен для усвоения всеми нами – это закон Паскаля.
Закон Паскаля не особенно сложен для восприятия и если сопоставить его с теми же законами Ньютона или законом Ома, то разобраться в нем проще. Но всё равно мы рассмотрим его детально и осмыслим :)! Ведь сталкиваемся мы с работой этого закона повсеместно, хотя, конечно же, совершенно не задумываемся об этом.
Где мы можем встретить закон Паскаля?
Наверняка многие ездят на автобусах или личных автомобилях, а там используются гидравлические тормозные системы. Без этих систем не получится выполнить эффективное торможение.
Ведь классические механические тормоза не всегда способны справиться с большими нагрузками. Если удержать автомобиль, массой 2 т ещё можно с помощью простой педальки с механической тягой, то остановить грузовик массой 30 т будет совсем не просто!
Получается, гидравлическая тормозная система способна увеличить силу, приложенную к тормозному диску?
Да, именно так! Это, как раз -таки, и есть работа закона Паскаля.
Аналогичный физический эффект используется во всех гидравлических усилителях. Это могут быть гидроножницы, гидравлический пресс и многие другие варианты применения в машинах и механизмах. Главное преимущество – возможность увеличить силу на выходе. Как же это происходит? Причем тут вообще закон Паскаля? А давайте вспомним, как он звучит.
Формулировка закона Паскаля
Давление на жидкость или газ, передается в любую точку без изменений во всех направлениях.
Так закон Паскаля записан в учебнике. Вроде бы всё и понятно. А вроде бы и опять какая-то каша. Но самая большая проблема в осмыслении появляется когда мы видим вот такую формулу.
Это запись закона Паскаля. Но тут совсем ничего не понятно :)…
Для начала, нужно понимать, что такое давление.
Давление – это некоторая физическая величина, которая описывается, как отношение силы к площади, на которую она воздействует.
Представить это довольно легко.
Понятно, что некоторую силу можно оказывать на некоторое тело. Для этого тело должно воздействовать на другое тело. Очевидно, что если сила оказывает воздействие широкой точкой приложения, то оказываемое давление будет меньше.
Представьте, что идёте по снегу на снегоступах или на кониках. Коньки проваливаются в глубокий снег, а снегоступы нет. Почему?
Площадь снегоступа больше, чем площадь лезвия конька.
Значит, снегоступ оказывает меньшее давление, а толща снега способна такое давление выдержать, что уже нельзя сказать про давление, оказываемое на снег коньками. Или, сила в случае снегоступа распределена по всему снегоступу, а в случае конька- по всему коньку.
Очевидно, что это разные величины. Также очевидно, что чем больше площадь, тем слабее воздействие. Вот эту характеристику и назвали давлением. В жидкости или газе ситуация аналогичная. Те же самые механические воздействия.
Теперь вернемся к формулировке закона Паскаля. Там есть фраза “передается в любую точку без изменений во всех направлениях.”
Именно это есть ключ к пониманию закона Паскаля. Именно это явление в результате многочисленных опытов и обнаружил ученый.
Самая простая демонстрация явления – шар Паскаля.
Это устройство было изготовлено специально для демонстрации равномерного распределения давления внутри жидкости или газа без изменений.
Надавливаешь на ручку и струи жидкости вырываются из каждого отверстия с одинаковой силой вне зависимости от расположения отверстия на шарике. Это может означать только одно. Что точка приложения тут роли не играет, а после оказания воздействия усилие это одинаково расходится во все отверстия.
Но если это так, то и в подобной системе обозначенный принцип будет выполняться
Это, кстати говоря, принципиальная схема простого гидравлического пресса.
Если записать, что давление одинаково, то получится нечто типа p1=p2=const
Само p, или давление, как мы помним равно F/S. Т.е. сила, приложенная к жидкости, разделить на площадь её приложения. А внутри у нас давление одинаково. Ведь Паскаль так сказал и доказал 🙂
Вот и выходит, что p1=p2 и F1/S1 = F2/S2. Нашли то самое неясное выражение, которое всех ставит в тупик. Оно следует из равенства давлений.
Применение закона Паскаля
Ну вот и получили мы некоторый гидравлический рычаг, который может дать выигрыш в силе. Эта схема используется во всех гидравлических системах для усиления нажатия. Хитрая организация гидравлических каналов тут роли не играет. Зато играет роль, что давление во все стороны одинаково распространяется.
Не забываем подписываться на канал и ставить нравится!
Источник
Определение и принцип гидравлического пресса
Определение
Гидравлический пресс – это машина, которая действует на основе законов движения и равновесия жидкостей.
Закон Паскаля лежит в основе принципа действия гидравлического пресса. Название этого устройства происходит от греческого слова гидравликос – водяной. Гидравлическим прессом называют гидравлическую машину, которая используется для прессования (сдавливания). Гидравлический пресс используют там, где необходима большая сила, например, при выдавливании масла из семян. При помощи современных гидравлических прессов можно получать силу до ${10}^8$ньютонов.
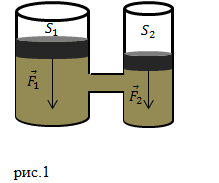
Основу гидравлической машины составляют два цилиндра разного радиуса с поршнями (рис.1), которые соединены трубой. Пространство в цилиндрах под поршнями обычно заполняют минеральным маслом.

Для того чтобы понять принцип действия гидравлической машины следует вспомнить, что такое сообщающиеся сосуды и в чем смысл закона Паскаля.
Сообщающиеся сосуды
Сообщающимися называют сосуды, соединенные между собой и в которых жидкость может свободно перетекать из одного сосуда в другой. Форма сообщающихся сосудов может быть разной. В сообщающихся сосудах жидкость одной плотности устанавливается на одном уровне, если давления над свободными поверхностями жидкости одинаковы.
Из рис.1 мы видим, что конструктивно гидравлическая машина – это два сообщающихся сосуда разного радиуса. Высоты столбов жидкости в цилиндрах будут одинаковыми, если на поршни не действуют силы.
Закон Паскаля
Закон Паскаля говорит нам о том, что давление, которое оказывают внешние силы на жидкость, передаются ей без изменения во все ее точки. На законе Паскаля основано действие многих гидравлических устройств: прессов, тормозных систем, гидроприводов, гидроусилителей и т.д.
Принцип действия гидравлического пресса
Одним из самых простых и старых устройств основанных на законе Паскаля является гидравлический пресс, в котором небольшая сила $F_1$, прикладываемая к поршню небольшой площади $S_1$, преобразуется в большую силу $F_2$, которая воздействует на площадь большой площади $S_2$.
Давление, которое создает поршень номер один, равно:
[p_1=frac{F_1}{S_1}left(1right).]
Давление второго поршня на жидкость составляет:
[p_2=frac{F_2}{S_2}left(2right).]
Если поршни находятся в равновесии то давления $p_1$ и $p_2$ равны, следовательно, мы можем приравнять правые части выражений (1) и (2):
[frac{F_1}{S_1}=frac{F_2}{S_2}left(3right).]
Определим, каким будет модуль силы, прикладываемой к первому поршню:
[F_1=F_2frac{S_1}{S_2}(4)]
Из формулы (4), видим, что величина $F_1$ больше модуля силы $F_2$ в $frac{S_1}{S_2}$ раз.
И так, применяя гидравлический пресс можно небольшой силой уравновесить гораздо большую силу. Отношение $frac{F_1}{F_2}$ показывает выигрыш в силе.
Пресс работает так. Тело, которое необходимо спрессовать, укладывают на платформу, которая лежит на большом поршне. С помощью малого поршня создают высокое давление на жидкость. Большой поршень вместе со сжимаемым телом поднимается, упирается в неподвижную платформу, находящуюся над ними, тело сжимается.
Из малого цилиндра в большой жидкость перекачивают повторным движением поршня малой площади. Делают это следующим образом. Малый поршень поднимается, открывается клапан, при этом в пространство под малым поршнем засасывается жидкость. Когда малый поршень опускается жидкость, оказывая на клапан давление, его закрывает, при этом открывается клапан, который пропускает жидкость в большой сосуд.
Примеры задач с решением
Пример 1
Задание. Каким будет выигрыш в силе у гидравлического пресса, если при действии на малый поршень (площадью $S_1=10 {см}^2$) с силой $F_1=800$ Н, получают силу, воздействия на большой поршень ($S_2=1000 {см}^2$) равной $F_2=72000 $ Н?
Какой выигрыш в силе получался бы у этого пресса, если бы отсутствовали силы трения?
Решение. Выигрышем в силе называют отношение модулей полученной силы к приложенной:
[frac{F_2}{F_1}=frac{72000}{800}=90.]
Используя формулу, полученную для гидравлического пресса:
[frac{F_1}{S_1}=frac{F_2}{S_2}left(1.1right),]
найдем выигрыш в силе при отсутствии сил трения:
[frac{F_2}{F_1}=frac{S_2}{S_1}=frac{1000}{10}=100.]
Ответ. Выигрыш в силе в прессе при наличии сил трения равен $frac{F_2}{F_1}=90.$ Без трения он
был бы равен $frac{F_2}{F_1}=100.$
Пример 2
Задание. Используя гидравлический подъемный механизм, следует поднять груз имеющий массу $m$. Какое число раз ($k$) нужно опустить малый поршень за время $t$, если за один раз он опускается на расстояние $l$? Отношение площадей поршней подъемника равно: $frac{S_1}{S_2}=frac{1}{n}$ ($n>1$). Коэффициент полезного действия машины составляет $eta $ при мощности его двигателя $N$.
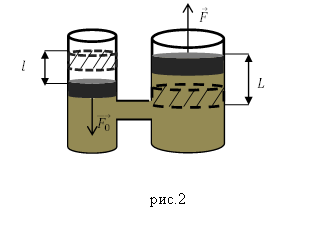
Решение. Принципиальная схема работы гидравлического подъемника изображена на рис.2., она аналогична работе гидравлического пресса.
В качестве основы для решения задачи используем выражение, связывающее мощность и работу, но при этом учтем, КПД подъемника, тогда мощность равна:
[N=frac{eta A}{t}to A=eta Ntleft(2.1right).]
Работу производят с целью груз поднять, значит, ее найдем как изменение потенциальной энергии груза, за ноль потенциальной энергии будем считать энергию груза в месте начала его подъема ($E_{p1}$=0), имеем:
[A=E_{p2}-E_{p1}=E_{p2}=mgh left(2.2right),]
где $h$ – высота, на которую подняли груз. Приравняв правые части формул (2.1) и (2.2), найдем высоту, на которую подняли груз:
[eta Nt=mghto h=frac{eta Nt}{mg}left(2.3right).]
Работу, выполняемую силой $F_0$, при перемещении малого поршня найдем как:
[А_1=F_0l left(2.4right),]
Работа силы, которая двигает большой поршень вверх (сжимает гипотетическое тело), равна:
[А_2=FL .]
[А_1=А_2to F_0l=FL]
[frac{F_0}{F}=frac{L}{l}=frac{S_1}{S_2}left(2.5right),]
где $L$ – расстояние, на которое сдвигается большой поршень за один ход. Из (2.5) имеем:
[frac{S_1}{S_2}=frac{L}{l}to L=frac{S_1}{S_2}l left(2.6right).]
Для того чтобы найти количество ходов поршней (число раз которое опустится малый поршень или поднимется большой) следует высоту поднятия груза разделить на расстояние на которое сдвигается большой поршень за один ход:
[k=frac{h}{L}=frac{eta NtS_2}{mgS_1l}=frac{eta Ntn}{mgl}.]
Ответ. $k=frac{eta Ntn}{mgl}$
Читать дальше: закон Архимеда.
Источник
Давление
Действие силы на твердое тело зависит не только от модуля этой силы, но и от площади поверхности тела, на которую она действует. Взаимодействие жидкостей и газов с твердыми телами, а также взаимодействие между соседними слоями жидкости или газа тоже происходит не в отдельных точках, а на определенной поверхности их соприкосновения. Поэтому для характеристики подобных взаимодействий введено понятие давления.
Давлением р называют величину, равную отношению модуля силы давления F, действующей перпендикулярно поверхности, к площади 5 этой поверхности:
p=F/S. (5.1)
При равномерном распределении сил давления давление на всех участках поверхности одинаково и численно равно силе давления, действующей на поверхность единичной площади.
Единицу давления устанавливают из формулы (5.1). В СИ за единицу давления принято давление, вызываемое силой 1 Н, равномерно распределенной по перпендикулярной к ней поверхности площадью 1 м2. Эту единицу давления называют паскаль (Па): 1 Па=1 Н/м2.
Часто используют и следующие внесистемные единицы давления:
- техническая атмосфера (ат): 1 ат=9,8·104 Па;
- физическая атмосфера (атм), равная давлению, производимому столбом ртути высотой 760 мм. Как показано в § 24, 1 атм = 1,033 ат = 1,013·105 Па;
- миллиметр ртутного столба (мм рт. ст.): 1 мм рт. ст. » 133,3 Па;
- бар (в метеорологии используют миллибар); 1 бар=105 Па, 1 мбар=102 Па.
Закон Паскаля для жидкостей и газов
Твердые тела передают производимое на них извне давление по направлению действия силы, вызывающей это давление. Совсем иначе передают внешнее давление жидкости и газы.
Рассмотрим следующий эксперимент (рис. 48). В сосуде, закрытом пробкой, находится вода. В пробку вставлены три одинаковые по диаметру трубки, нижние отверстия которых находятся в воде на одинаковой глубине, но направлены в разные стороны (вниз, вбок и вверх), а также не достающая до воды трубка, к которой подсоединен резиновый баллон от пульверизатора. Закачивая с его помощью воздух в сосуд, мы увеличиваем давление, оказываемое воздухом на поверхность воды в сосуде. Замечаем, что при этом во всех трех трубках вода поднимается до одной и той же высоты. Следовательно, неподвижная жидкость, находящаяся в замкнутом сосуде, передает производимое на нее внешнее давление по всем направлениям одинаково (т.е. без изменения).
Наблюдения показывают, что так же передают внешнее давление и газы, находящиеся в закрытом сосуде. Описанная закономерность была впервые обнаружена французским ученым Паскалем и получила название закона Паскаля.
Гидростатическое давление
На каждую молекулу жидкости, находящейся в поле тяготения Земли, действует сила тяжести. Под действием этих сил каждый слой жидкости давит на расположенные под ним слои. По закону Паскаля это давление передается жидкостью по всем направлениям одинаково. Следовательно, в жидкостях существует давление, обусловленное силой тяжести.
Наблюдения показывают, что жидкость, находящаяся в сосуде в состоянии покоя, давит на дно и стенки сосуда и на любое тело, погруженное в эту жидкость. Давление, оказываемое покоящейся жидкостью на любую соприкасающуюся с ней поверхность, называют гидростатическим.
Формула гидростатического давления
Гидростатическое давление можно определить с помощью прибора, называемого гидростатическими весами Паскаля (рис. 49). В подставке П, сквозь которую проходит кольцевой патрубок К, можно поочередно герметично закреплять сосуды С любой формы, не имеющие дна. Подвижным дном этих сосудов служит подвешенная на коромысле равноплечих весов плоская круглая площадка Д, расположенная вблизи нижнего отверстия патрубка К. Эта площадка прижимается к торцу патрубка силой, вызываемой тем, что на чашку весов, подвешенную на другом их коромысле, ставится гиря Г. К подставке П прикреплена линейка Л, по которой определяют высоту h жидкости в сосуде, закрепленном на подставке.
Опыт производят так. На под-ставке укрепляют сосуд, имеющий форму прямого кругового цилиндра. В него наливают воду до тех пор, пока вес этой воды не станет равным весу гири, поставленной на правую чашку весов, т.е. Рж=Рг. (Поддержание этого количества воды автоматически обеспечивается самим прибором, так как если вес воды в сосуде превысит вес гири, дно приоткроется и излишек воды вытечет.)
В цилиндрическом сосуде вес жидкости Pж=rжghS, где ж=rж – плотность жидкости, g – ускорение свободного падения, h – высота столба жидкости, S – площадь основания цилиндра, поэтому на дно сосуда жидкость оказывает давление
р=Pж/S=rжgh. (5.2)
Формула (5.2) определяет значение гидростатического давления.
Теоретический вывод формулы гидростатического давления
Выделим внутри покоящейся жидкости неподвижный элемент ее объема DV в виде прямого кругового цилиндра высотой h с основаниями, имеющими малую площадь DS, параллельными свободной поверхности жидкости (рис. 50). Верхнее основание цилиндра находится от поверхности жидкости на глубине h1, а нижнее – на глубине h2>h1.
На выделенный элемент объема жидкости действуют по вертикали три силы: силы давления F1=p1DS и F2=p2DS (где p1 и p2 – значения гидростатического давления на глубинах h1 и h2) и сила тяжести Fт=rgDV =rghDS.
Выделенный нами элемент объема жидкости покоится, значит, F1+F2+Fт=0, а следовательно, равна нулю и алгебраическая сумма проекций этих сил на вертикальную ось, т. е. p2DS-p1DS-rghDS=0, откуда получаем
p2-p1=rgh. (5.3)
Пусть теперь верхняя грань выделенного цилиндрического объема жидкости совпадает с поверхностью жидкости, т.е. h1=0. Тогда h2=h и p2=p, где h – глубина погружения, а р – гидростатическое давление на данной глубине. Считая, что на поверхности жидкости давление р1=0 (т.е. без учета внешнего давления на поверхность жидкости), из (5.3) получаем формулу для гидростатического давления р=rgh, которая совпадает с формулой (5.2).
Сообщающиеся сосуды
Сообщающимися называют сосуды, имеющие между собой канал, заполненный жидкостью. Наблюдения показывают, что в сообщающихся сосудах любой формы однородная жидкость всегда устанавливается на одном уровне.
Иначе ведут себя разнородные жидкости даже в одинаковых по форме и размерам сообщающихся сосудах. Возьмем два цилиндрических сообщающихся сосуда одинакового диаметра (рис. 51), на их дно нальем слой ртути (заштрихован), а поверх него в цилиндры нальем жидкости с разными плотностями, например r2<r1 (слой ртути нужен для того, чтобы жидкости не смешивались). Мы увидим, что если эти жидкости находятся в состоянии покоя, их уровни h1 и h2 различны (h2>h1).
Мысленно выделим внутри трубки, соединяющей сообщающиеся сосуды и заполненнной ртутью, площадку площади S, перпендикулярную горизонтальной поверхности. Так как жидкости покоятся, давление на эту площадку слева и справа одинаково, т.e. p1=p2. Согласно формуле (5.2), гидростатическое давление p1=r1gh1 и p2=r2gh2. Приравняв эти выражения, получаем r1h12h2, откуда = r
h1/h2=r2/r1. (5.4)
Следовательно, разнородные жидкости в состоянии покоя устанавливаются в сообщающихся сосудах таким образом, что высоты их столбов оказываются обратно пропорциональными плотностям этих жидкостей.
Если r1=r2, то из формулы (5.4) следует, что h1=h2, т.е. однородные жидкости устанавливаются в сообщающихся сосудах на одинаковом уровне.
Принцип действия гидравлического пресса
Гидравлический пресс представляет собой два сообщающихся сосуда цилиндрической формы и разного диаметра, в которых имеются поршни, площади которых S1 и S2 различны (S2 >> S1). Цилиндры заполнены жидким маслом (обычно трансформаторным) . Схематически устройство гидравлического пресса изображено на рис. 52 (на этом рисунке не показаны резервуар с запасом масла и система клапанов).
Без нагрузки поршни находятся на одном уровне. На поршень S1 действуют силой F1, а между поршнем S2 и верхней опорой закладывают тело, которое нужно прессовать.
Сила F1, действуя на поршень S1, создает в жидкости дополнительное давление р=F1/S1. По закону Паскаля это давление передается жидкостью по всем направлениям без изменения. Следовательно, на поршень S2 действует сила давления
F2=pS2=F1S2/S1.
Из этого равенства следует, что
F2/F1=S2/S1. (5.5)
Следовательно, силы, действующие на поршни гидравлического пресса, пропорциональны площадям этих поршней. Поэтому с помощью гидравлического пресса можно получить выигрыш в силе тем больший, чем S2 больше S1.
Гидравлический пресс широко используется в технике.
Источник
Источник
