Закон сообщающихся сосудов невесомости

Это описывает общая теория относительности. Космологи (а также астрофизики), конечно, тоже физики =) Но от всех остальных они отличаются тем, что постоянно работают в общей теории относительности, которая и описывает то самое сверхсветовое движение. Остальным обычно хватает более узкой специальной (нем. spezielle — частная) теории относительности, которая не описывает гравитации, и поэтому там сверхсветового движения нет.
Что запрещает специальная теория относительности? Движение материальных объектов со скоростью больше скорости света. Тут все слова важны:
Движение материальных объектов — при этом, скажем, расстояние между двумя объектами в системе третьего может увеличиваться быстрее скорости света. В специальной теории относительности такая скорость не равна скорости одного из объектов в системе отсчёта другого. (Первая получается простым сложением, как и положено геометрически, а вторая — по релятивистской «формуле сложения скоростей».)
Движение материальных объектов — при этом, например, тень или солнечный зайчик могут двигаться быстрее скорости света, как это и предписывает геометрическая оптика.
[Комар на Земле движется со скоростью 5 мм/сек — тень комара на Луне движется со скоростью 12.7 км/сек.] Иллюстрация: Prof Gregory J Gbur / skullsinthestars.com
Другое дело, что свет распространяется не мгновенно, и поэтому положение тени будет соответствовать чуть более раннему положению объекта.
Есть ещё запрет на передачу информации быстрее скорости света, но нам он сейчас не нужен.
Что к этому добавляет общая теория относительности? Расширение Вселенной. Запрет на сверхсветовое движение, который мы только что разобрали, по-прежнему выполняется — но только в малом.
Что это значит? Представьте себе, что вы муравей и живёте на воздушном шарике. У вас есть муравьиный дом, муравьиная работа и максимальная муравьиная скорость. Если вы идёте с работы домой, то ваше расстояние от работы не может увеличиваться быстрее, чем ваша максимальная скорость.
А теперь представьте, что шарик начали надувать. Тогда вы можете даже стоять, а расстояние до работы всё равно будет увеличиваться; а уж если пойти, то оно может увеличиваться даже быстрее вашей максимальной скорости. Правда, если шарик надувают совсем быстро, то и до дома вы не дойдёте, как бы ни бежали.
Почти буквально то же самое происходит при расширении Вселенной, только максимальная скорость ограничена не вами, а физическими законами, на месте двумерной поверхности шарика оказывается наше трёхмерное пространство, и у нас нет возможности посмотреть на происходящее снаружи (может, никакого «снаружи» и нет).
Мечты об окончательной теории. То, что всех примиряет общая теория относительности, на самом деле не совсем правда. Заметная часть физиков работает не с классическими объектами (как в моём описании), а с квантовыми. Их можно поселить в общую теорию относительности, но в таком гибриде ужа с ежом будут логические противоречия — их не видно во всех реальных физических экспериментах, но чтобы их исправить, нужно саму гравитацию описать квантовым образом, а этого мы не умеем. (Если бы эти противоречия было видно, построить квантовую теорию гравитации было бы гораздо проще!)
Источник
Сообщающиеся сосуды – это сосуды, соединенные между собой ниже уровня жидкости в каждом из сосудов. Таким образом жидкость может перемещаться из одного сосуда в другой.
Перед тем как понять принцип действия сообщающихся сосудов и варианты их использования необходимо определиться в понятиях, а точнее разобраться с основным уравнением гидростатики.
Итак, сообщающиеся сосуды имеют одно общее дно и закон о сообщающихся сосудах гласит:
Какую бы форму не имели такие сосуды, на поверхности однородных жидкостей в состоянии покоя на одном уровне действует одинаковое давление.
Для иллюстрации этого закона и возможностей его применения начнем с рассмотрения основного уравнения гидростатики.
Основное уравнение гидростатики
P = P1 + ρgh
где P1 – это среднее давление на верхний торец призмы,
P – давление на нижний торец,
g – ускорение свободного падения,
h – глубина погружения призмы под свободной поверхностью жидкости.
ρgh – сила тяжести (вес призмы).
Звучит уравнение так:
Давление на поверхность жидкости, произведенное внешними силами, передается в жидкости одинаково во всех направлениях.
Из написанного выше уравнения следует, что если давление, например в верхней точке изменится на какую-то величину ΔР, то на такую же величину изменится давление в любой другой точке жидкости
Доказательство закона сообщающихся сосудов
Возвращаемся к разговору про сообщающиеся сосуды.
Предположим, что имеются два сообщающихся сосуда А и В, заполненные различными жидкостями с плотностями ρ1 и ρ2. Будем считать, что в общем случае сосуды закрыты и давления на свободных поверхностях жидкости в них соответственно равны P1 и P2.
Пусть поверхностью раздела жидкостей будет поверхность ab в сосуде А и слой жидкости в этом сосуде равен h1. Определим в заданных условиях уровень воды в сообщающихся сосудах – начнем с сосуда В.
Гидростатическое давление в плоскости ab, в соответствии с уравнение гидростатики
P = P1 + ρgh1
если определять его, исходя из известного давления P1 на поверхность жидкости в сосуде А.
Это давление можно определить следующим образом
P = P2 + ρgh2
где h2 – искомая глубина нагружения поверхности ab под уровнем жидкости в сосуде В. Отсюда выводим условие для определения величины h2
P1 + ρ1gh1 = P2 + ρ2gh2
В частном случае, когда сосуды открыты (двление на свободной поверхности равно атмосферному), а следовательно P1 = P2 = Pатм , имеем
ρ1h1 = ρ2h2
или
ρ1 / ρ2 = h2 / h1
т.е. закон сообщающихся сосудов состоит в следующем.
В сообщающихся сосудах при одинаковом давлении на свободных поверхностях высоты жидкостей, отсчитываемые от поверхности раздела, обратно пропорциональны плотностям жидкостей.
Свойства сообщающихся сосудов
Если уровень в сосудах одинаковый, то жидкость одинаково давит на стенки обоих сосудов. А можно ли изменить уровень жидкости в одном из сосудов.
Можно. С помощью перегородки. Перегородка, установленная между сосудами перекроет сообщение. Далее доливая жидкость в один из сосудов мы создаем так называемый подпор – давление столба жидкости.
Если затем убрать перегородку, то жидкость начнет перетекать в тот сосуд где её уровень ниже до тех пор пока высота жидкости в обоих сосудах не станет одинаковой.
В быту этот принцип используется например в водонапорной башне. Наполняя водой высокую башню в ней создают подпор. Затем открывают вентили, расположенные на нижнем этаже и вода устремляется по трубопроводам в каждый подключенный к водоснабжению дом.
Приборы основанные на законе сообщающихся сосудов
На принципе сообщающихся сосудов основано устройство очень простого прибора для определения плотности жидкости. Этот прибор представляет собой два сообщающихся сосуда – две вертикальные стеклянные трубки А и В, соединенные между собой изогнутым коленом С. Одна из вертикальных трубок заполняется исследуемой жидкостью, а другая жидкостью известной плотности ρ1 (например водой), причем в таких количествах, чтобы уровни жидкости в среднем колене находились на одной и той же отметке прибора 0.
Затем измеряют высоты стояния жидкостей в трубках над этой отметкой h1 и h2. И имея ввиду, что эти высоты обратно пропорциональны плотностям легко находят плотность исследуемой жидкости.
В случае, когда оба сосуде заполнены одной и той же жидкостью – высоты, на которые поднимется жидкость в сообщающихся сосудах, будут одинаковы. На этом принципе основано устройство так называемого водометного стекла А. Его применяют для определения уровня жидкости в закрытых сосудах, например резервуарах, паровых котлах и т.д.
Принцип сообщающихся сосудов заложен в основе ряда других приборов, предназначенных для измерения давления.
Применение сообщающихся сосудов
Простейшим прибором жидкостного типа является пьезометр, измеряющий давление в жидкости высотой столба той же жидкости.
Пьезометр представляет собой стеклянную трубку небольшого диаметра (обычно не более 5 мм), открытую с одного конца и вторым концом присоединяемую к сосуду, в котором измеряется давление.
Высота поднятия жидкости в пьезометрической трубке – так называемая пьезометрическая высота – характеризует избыточное давление в сосуде и может служить мерой для определения его величины.
Пьезометр – очень чувствительный и точный прибор, но он удобен только для измерения небольших давлений. При больших давлениях трубка пьезометра получается очень длинной, что усложняет измерения.
В этом случае используют жидкостные манометры, в которых давление уравновешивается не жидкостью, которой может быть вода в сообщающихся сосудах, а жидкостью большей плотности. Обычно такой жидкостью выступает ртуть.
Так как плотность ртути в 13,6 раз больше плотности воды и при измерении одних и тех же давлений трубка ртутного манометра оказывается значительно короче пьезометрической трубки и сам прибор получается компактнее.
В случае если необходимо измерить не давление в сосуде, а разность давлений в двух сосудах или, например, в двух точках жидкости в одном и том же сосуде применяют дифференциальные манометры.
Сообщающиеся сосуды находят применение в водяных и ртутных приборах жидкостного типа, но ограничиваются областью сравнительно небольших давлений – в основном они применяются в лабораториях, где ценятся благодаря своей простоте и высокой точности.
Когда необходимо измерить большое давление применяются приборы основанные на механических принципах. Наиболее распространенный из них – пружинный манометр. Под действием давления пружина манометра частично распрямляется и посредством зубчатого механизма приводит в движение стрелку, по отклонению которой на циферблате показана величина давления.
Видео по теме
Ещё одним устройством использующим принцип сообщающихся сосудов хорошо знакомым автолюбителем является гидравлический пресс(домкрат). Конструктивно он состоит из двух цилиндров: одного большого, другого маленького. При воздействии на поршень малого цилиндра на большой передается усилие во столько раз большего давления во сколько площадь большого поршня больше площади малого.
Вместе со статьей “Закон сообщающихся сосудов и его применение.” читают:
Источник
Закон сообщающихся сосудов гласит: высоты столбов жидкости в сообщающихся емкостях равны. Однако это правило действует не всегда. Все зависит от плотности веществ, налитых в сосуды. В статье мы с помощью экспериментов разберемся, в каких условиях закон сообщающихся сосудов верен. Узнаем, как он помогает судам переплывать через плотины, а строителям возводить здания.
Давление в сообщающихся емкостях
Представьте себе два сосуда любой формы и размера. Они сообщаются друг с другом в нижней части при помощи трубки, в которой установлен кран. Пусть пока он будет закрыт. Давайте в левый сосуд нальем какое-то вещество. Высоту столба этой жидкости (расстояние от поверхности до дна) в первой емкости мы обозначим h1, а плотность вещества в ней — ρ1.
В правый сосуд мы нальем раствор, плотность которого будет ρ2. Высоту столба во второй емкости обозначим h2. Допустим, мы подобрали значения h1 и h2 так, что жидкости не будут перетекать, если открыть кран. Отметим, что в нашем опыте вещества, налитые в первую и вторую емкости, не смешиваются между собой, то есть они имеют разные физические характеристики. В данный момент эти жидкости находятся в равновесии. Что можно сказать о давлении у самого дна первого сосуда (P1) и второго (P2)?
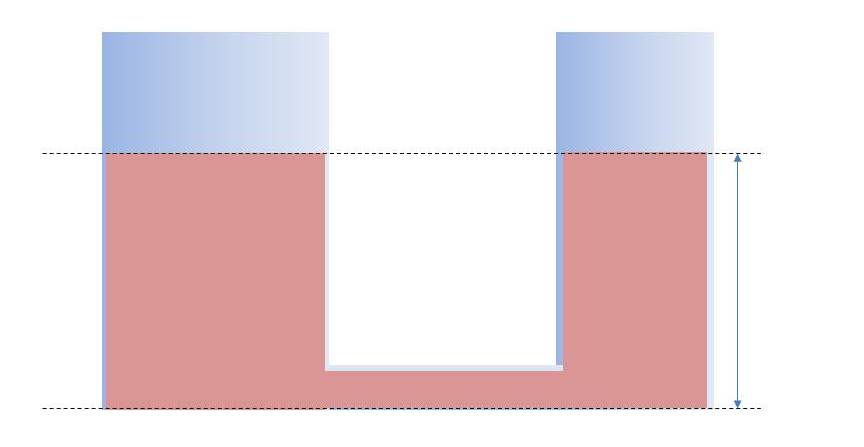
Так как жидкости в равновесии, то и давления у них одинаковые. Представьте себе, что между двумя сосудами не кран, а тонкая перегородка, например, листик бумаги. На него слева и справа будут действовать одинаковые силы, то есть P1=P2. Это условие равновесия. Выразим давление через плотность жидкости и высоту столба. Формула достаточно простая.
Давление, создаваемое неподвижной жидкостью, называется гидростатическим. Вот его формула:
P=ρ*g*h, где:
ρ — плотность жидкости.
g — ускорение свободного падения.
h — высота столба.
В первом сосуде гидростатическое давление рассчитаем по формуле:
P1=ρ1*g*h1.
Соответственно, во втором сосуде оно рассчитывается по формуле:
P2=ρ2*g*h2.
Подставим эти два выражения в условие равновесия:
ρ1*g*h1=ρ2*g*h2.
Разделим левую и правую часть на g. Остается:
ρ1*h1=ρ2*h2.
Это условие равновесия разных жидкостей в сообщающихся емкостях. Как видим, оно зависит от плотности налитых растворов и высоте, на которую они поднимаются.
Закон сообщающихся сосудов
Рассмотрим частный случай, когда в обеих емкостях одинаковая жидкость. Как этот факт отражается на формуле условия равновесия? По условию задачи:
ρ1= ρ2=ρ.
Перепишем условие равновесия:
ρ*h1=ρ*h2.
Сократим плотность в левой и правой частях равенства. Получим:
h1=h2.
Это математическое выражение закона сообщающихся сосудов. Сформулируем его словами: свободные поверхности однородной жидкости в сообщающихся сосудах располагаются на одинаковой высоте. Интересно, что закон сообщающихся сосудов в невесомости не действует. Это происходит по той причине, что у жидкости нулевой вес.
В левой и правой емкостях не обязательно должно быть одинаковое вещество. В таком случае закон работать не будет, но условие равновесия останется справедливым. Для различных жидкостей справедливо правило: если плотность первой меньше, чем второй, то высота ее столба будет больше.
Влияет ли форма емкости на перетекание жидкостей
Справедлив ли закон сообщающихся сосудов, если емкость сужается к основанию, расширяется или же имеет очень сложную форму? Независимо от конфигурации, высота столба жидкости будет одна и та же. При этом сообщающихся сосудов может быть не два, а сколь угодно много. Какой бы изощренной ни была форма, если все емкости сообщаются, а жидкость в них налита одинаковая, то высота столба будет одной и той же.

Возьмем два шприца разного диаметра, соединенных трубкой. Наполним их водой. Мы видим, что высота свободной поверхности жидкости в обеих емкостях равна. Если мы наклоняем один шприц, высота столба жидкости остается одинаковой в одном и в другом. Опустим или поднимем один из шприцев. Что мы видим? Уровень воды во втором поднимается или опускается так, чтобы выровняться с уровнем в первом.
Наполним шприцы жидкостями разной плотности — водой и концентрированным раствором соли. Дождемся, пока они придут в равновесие. Что мы видим? Несмотря на то, что внешне жидкости в обоих шприцах выглядят одинаково, высота столба в одном из них больше. Плотность солевого раствора примерно на 20% выше, чем обычной воды. Высота столба во столько раз меньше, во сколько раз больше этот показатель.
Роль закона на практике
В строительстве очень важно, чтобы некоторые поверхности были строго горизонтальными, например, фундамент домов на наклонной улице. Чтобы устанавливать различные поверхности строго горизонтально или вертикально, существует плотницкий уровень. Это устройство представляет собой немного изогнутую трубочку. Она закрыта с обеих сторон, а посередине есть пузырек. Трубка вмонтирована в короб. В окошко виден только пузырек. Он всегда стремится всплыть. Если поверхность строго горизонтальна, то пузырек располагается посередине.

Уровень имеет существенный недостаток: он не позволяет проверять большие поверхности, например фундамент. Однако знание закона сообщающихся сосудов помогло сделать устройство, которое называется жидкостный уровень. Оно представляет собой длинную гибкую трубку, заполненную водой.
Нарисуем фундамент дома, чтобы проверить, будет ли он строго горизонтальным, если использовать данное устройство. Поднимая и опуская трубку, добьемся того, чтобы уровень воды в ней совпадал с нарисованной линией фундамента. Понаблюдаем за уровнем воды во втором конце устройства. Если он выше или ниже первого, значит, нарисованный нами фундамент не является строго горизонтальным.
Плотины
Есть еще одна область применения закона сообщающихся сосудов. Чтобы поставить на реках гидроэлектростанции, сооружают плотины. Уровень воды в верхнем бьефе и в нижнем может отличаться на десятки метров. Существует плотины высотой около 100 метров. Если река судоходная, нужно сделать так, чтобы суда переходили из области над плотиной (верхний бьеф) в зону под ней. Как решают эту проблему? Меняют уровень воды с помощью шлюзов.
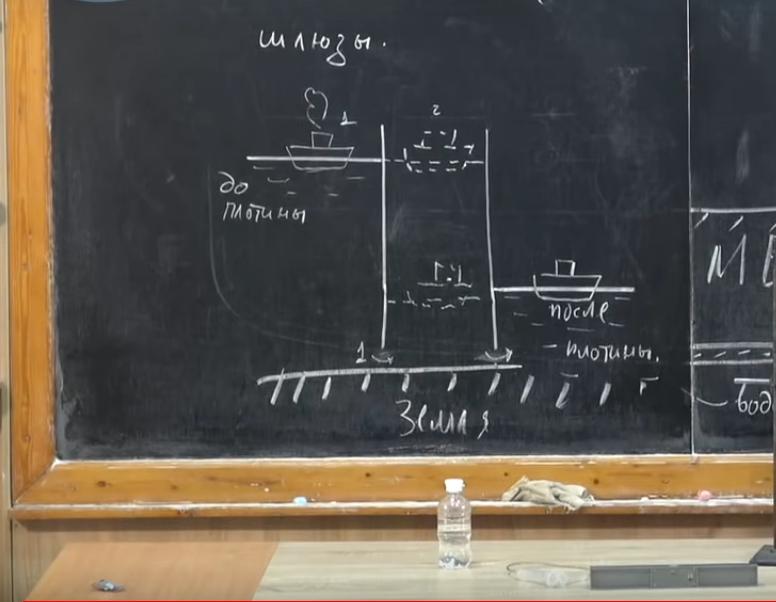
Представьте плотину. Нам нужно, чтобы корабль спустился сверху вниз. В шлюзе есть отверстия для воды. Также имеется двое ворот для кораблей. Если открыть отверстия до плотины, то вода начнет наполнять шлюз. После этого открывают первые ворота. Корабль спокойно проплывает по поднявшейся воде. Дальше нужно сделать так, чтобы она из шлюза вытекала. При этом корабль начинает опускаться вместе с уходящей водой. Когда ее уровень в шлюзе и в зоне за плотиной сравняется, открывают вторые ворота. Корабль поплывет в нижний бьеф.
Источник
Всем известно, что нужно сделать с чайником, чтобы из его носика полилась вода, – просто наклонить. А вот вопрос, можно ли перевести корабль через гору в море или другой водоем, вызовет у нас сомнение. Чтобы ответить на него, сначала следует узнать, что из себя представляют сообщающиеся сосуды.

Закон сообщающихся сосудов
Сообщающиеся сосуды – это взаимодействующие друг с другом сосуды, которые имеют общее дно.
Рис. 1. Сообщающиеся сосуды
Закон сообщающихся сосудов гласит, что в таких сосудах, какую бы форму они не имели, поверхности однородных жидкостей в состоянии покоя находятся на одном уровне, то есть давление, оказываемое на стенки на любом горизонтальном уровне является одинаковым.
Если же в сосуде жидкости разные, то уровень выше в сосуде, в котором жидкость обладает меньшей плотностью. То есть, если в один сосуд налить жидкость, обладающую одной плотностью, а во второй – другой, то при равновесии их уровни не будут одинаковыми. Следовательно отсюда можно вывести формулу:
ρ1/ρ2=h2/h1
Где:
- ρ – плотность жидкости;
- h – высота столба.
Также для сообщающихся сосудов важной является формула:
p=gρh
Где:
- g – ускорение свободного падения;
- ρ – плотность жидкости (кг/куб.м);
- h – глубина (высота столба жидкости).
Этой формулой определяется давление жидкости на дно сосуда.
Древним римлянам было неизвестно определение сообщающихся сосудов, поэтому их акведуки – водопроводы занимали огромную протяженность над поверхностью земли и строились с равномерным уклоном вниз.
Свойства сообщающихся сосудов
В сообщающихся сосудах уровень жидкости одинаковый. Это происходит потому, что жидкость производит одинаковое давление на стенки сосуда. Достичь разного уровня однородной жидкости в сообщающихся сосудах можно с помощью перегородки между ними.
Перегородка перекроет сообщение между сосудами, и тогда можно в один из них долить жидкость, чтобы уровень изменился. В данной ситуации возникает напор – давление, производимое весом столба жидкости высотой, равной разности уровней. И если убрать перегородку, то именно это давление станет причиной тому, что жидкость будет перетекать в тот сосуд, где ее уровень ниже, до тех пор, пока уровни не станут одинаковыми.
В жизни очень часто можно встретить естественный напор. И таких примеров довольно много. Например, им обладает вода в горных реках, когда падает с высоты. Плотина также является примером естественного напора. Чем она выше, тем больше будет напор воды, поднятой плотиной.
Применение закона о сообщающихся сосудах
Принцип действия сообщающихся сосудов используется при сооружении фонтанов, водопроводов, шлюзов. Чайник и его носик тоже являются сообщающимися сосудами, так как вода, налитая в чайник, заполняет носик и всю остальную часть до одинаковой высоты. Применение свойств таких сосудов, могут даже помочь провести корабль через гору. И для этого как раз понадобиться шлюз. Шлюз – это лифт для судов. Если водное пространство перегорожено плотиной, то уровень воды в водохранилище выше, чем в реке ниже по течению. И чтобы добраться до этого уровня, судно должно зайти в шлюз, который отгорожен двумя водными непроницаемыми воротами. Когда шлюз полностью заполняется водой, судно выходит из шлюза и продолжает свой путь (уровень воды в шлюзе и водохранилище выравнивается по закону сообщающихся сосудов).

Рис. 2. Шлюз
Что мы узнали?
Из этой темы по физики за 7 класс можно ясно понять, какие сосуды называются сообщающимися. Ими могут называться лишь те сосуды, обладающие общим дном, где жидкость может свободно перетекать из одного сосуда в другой. Также сообщающиеся сосуды играют огромную роль в нашей повседневной жизни, облегчая ее и помогая выходить из трудных ситуаций. Принципы сообщающихся сосудов лежат в основе различных чайников, кофейников, водомерных стекол на паровых котлах.
Тест по теме
Доска почёта
Чтобы попасть сюда – пройдите тест.
-
Алика Квегмайр
10/10
Яна Василькова
10/10
Елена Куренкова
9/10
Мария Егорова
8/10
Тимофей Черный
10/10
Максим Скарнович
10/10
Люба Музыченко
10/10
Владимир Шитов
9/10
Константин Никитич
9/10
Катя Пу
10/10
Оценка доклада
Средняя оценка: 4.2. Всего получено оценок: 843.
Источник
