Закрытый сосуд в виде прямоугольного параллелепипеда с ребрами
Справочные материалы
Призма. Виды призмы
Если вы уже знакомы с призмой, и хотите для себя просто что-то уточнить, то вам вполне может хватить таблицы, что дана в конце статьи.
Мы же поведем подробный разговор.
Призмой (n-угольной призмой) называется многогранник, составленный из двух равных многоугольников и , лежащих в параллельных плоскостях, и параллелограммов .

Указанные в определении равные многоугольники – основания призмы.
Боковые грани – все грани, кроме оснований (являются параллелограммами).
Боковые ребра – общие стороны боковых граней (параллельны между собой и равны).
Диагональ – отрезок, соединяющий две вершины призмы, не принадлежащие одной грани.

Высота призмы – перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания.

Диагональная плоскость – плоскость, проходящая через боковое ребро призмы и диагональ основания.
Диагональное сечение–пересечение призмы и диагональной плоскости.

Перпендикулярное сечение – пересечение призмы и плоскости, перпендикулярной ее боковому ребру.

Различают призмы прямые (боковые ребра перпендикулярны плоскости основания) и наклонные (не прямые).

Среди прямых призм выделяют правильные.
Правильная призма – это прямая призма, основанием которой является правильный многоугольник (равносторонний треугольник, квадрат, правильный шестиугольник и т.п.).

Частным случаем призмы является параллелепипед.
Параллелепипед – это призма, основаниями которой являются параллелограммы.
Среди параллелепипедов выделяют наклонные, прямые и прямоугольные параллелепипеды.

Прямой параллелепипед — это параллелепипед, у которого 4 боковые грани — прямоугольники.
Прямоугольный параллелепипед — это параллелепипед, у которого все грани — прямоугольники (или прямой параллелепипед с прямоугольником в основании).
Наклонный параллелепипед — это параллелепипед, боковые грани которого не перпендикулярны основаниям.
Частный случай прямоугольного параллелепипеда – куб.
Куб – прямоугольный параллелепипед, все грани которого – квадраты.

Далее – обещанная таблица, в которой собраны все основные виды призмы, с которыми приходится встречаться на ЕГЭ по математике
Вопросы для повторения:
– Что называется многогранником?
– Из каких частей состоит многогранник?
– Что называется гранью многогранника?
– Что называют диагональю многогранника?
Общие теоретические сведения
Призмой (n-угольной призмой) называется многогранник, составленный из двух равных многоугольников и , лежащих в параллельных плоскостях, и n параллелограммов …

Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы

Свойства призмы .(слайд 5)
Основания призмы являются равными многоугольниками.
Боковые грани призмы являются параллелограммами.
Боковые ребра призмы параллельны и равны.
Различают призмы прямые,наклонныеи правильные. (слайд 6,7,8)



Диагональным сечением призмы называется ее сечение плоскостью, проходящей через два боковых ребра, которые не лежат в одной грани.
(слайд 9)

Если секущая плоскость пересекает все боковые ребра призмы и перпендикулярна им, то получающееся при этом сечение называется перпендикулярным сечением призмы.

Площадь боковой поверхности призмы равна сумме площадей ее боковых граней.
Площадь полной поверхности призмы равна сумме площадей оснований и площади боковой поверхности.
.
Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы.
.
Площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения на длину бокового ребра.
.
Объем призмы
, где S – площадь основания, H – высота призмы.
Объем призмы можно найти, умножив площадь перпендикулярного сечения на длину бокового ребра. .
Частным случаем призмы является параллелепипед.
Параллелепипед– это призма, основаниями которой являются параллелограммы



Различают прямой, наклонный, прямоугольный параллелепипеды.
Свойства параллелепипеда
Длины непараллельных ребер прямоугольного параллелепипеда называют его линейными размерами (измерениями).
У прямоугольного параллелепипеда три измерения.
Объём прямоугольного параллелепипеда равен произведению трех его измерений.
Повтори необходимые формулы :
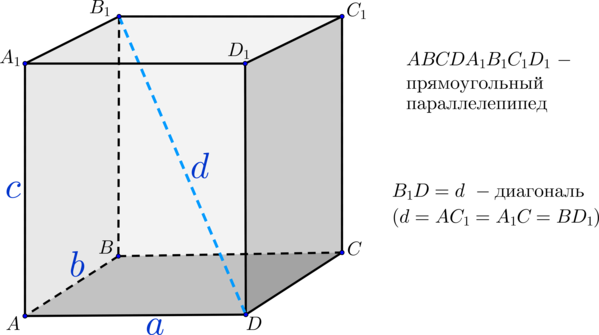
1. Прямоугольный параллелепипед
Пусть a, b, с – стороны, d – диагональ параллелепипеда,
Sn – полная поверхность.
V=a*b*c
Sб=P*H=2(a+b)*c
d2= a2+ b2+ c2
Sn=2(ab+bc+ac)
2.Куб
Пусть a – реброкуба.
V=a3
d=a
Sб=4a2
Sn=6a2
Проверь себя!
Ответь на теоретические вопросы по теме «Призма»
Опорные задачи.
Ребро куба равно a. Найдите: диагональ грани, диагональ куба, периметр основания, площадь грани, площадь диагонального сечения; площадь поверхности куба; периметр и площадь сечения, проходящего через концы трёх рёбер, выходящих из одной и той же вершины. (слайд 14)
Площадь боковой поверхности правильной четырёхугольной призмы равна 32 см2, а площадь полной поверхности 40 см2. Найдите высоту призмы. (слайд 15)
Расстояния между боковыми рёбрами наклонной треугольной призмы равны 2 см, 3 см и 4 см. Боковая поверхность призмы 45 см2. Найдите боковое ребро. (слайд 16)
В правильной n – угольной призме проведена плоскость под углом 600 к основанию так, что она пересекает все боковые грани призмы. Площадь основания равна 50 см2. Найдите площадь сечения.
Решение: Sосн=Sсеч*cos 600
Sсеч=100 см2
Существует ли призма, имеющая 50 рёбер? 54 ребра?
Решение: Число ребер n – угольной призмы 3n, поэтому призмы, имеющей 50 ребер, не существует, а 54 ребра имеет 18-угольная призма.
В правильной треугольной призме плоскость сечения BCА1 образует с плоскостью основания двугранный угол φ. Постройте линейный угол этого двугранного угла. Дайте объяснение.
Построение: Проведём из вершины A правильного треугольника ABC высоту AK. Точка K принадлежит ребру BC. Соответственно, отрезок А1К перпендикулярен ребру BC (по теореме о трёх перпендикулярах). Угол A1КА– искомый.

Задания части В.
1. Объем прямоугольного параллелепипеда равен 2. Чему будет равен объем параллелепипеда, если каждое его ребро увеличить в 3 раза.
Решение. Пусть ребра данного параллелепипеда равны a, b и c. Тогда имеем: V=abc=2. После увеличения каждого ребра в 3 раза его объём будет равен
V=3a*3b*3c =27 abc=27*2=54.
Ответ: 54.
2. Аквариум имеет форму прямоугольного параллелепипеда высотой 30 см. Если в него налить 30 л. воды, то до верхнего края останется 5 см. Сколько литров воды нужно, чтобы наполнить пустой аквариум доверху?
Решение. Пусть V и H соответственно объем и высота параллелепипеда.
V=SH . По условию V=30,H=25, тогда 25*S=30.
После заполнения пустого аквариума доверху H=30. Значит, 30*S=V.
Найдем отношение =, V=36 л.
Ответ: 36.
3. Кубик весит 10 гр. Сколько граммов будет весить кубик, ребро которого в 3 раза больше, чем ребро первого кубика, если оба кубика изготовлены из одинакового материала.
Решение. Пусть V- объём данного параллелепипеда. После увеличения каждого ребра в 3 раза, его объём будет равен 27 V.
, x=270 гр.
Ответ: 270.
Задания части С.
В кубе ABCDA1B1C1D1 найдите тангенс угла между прямой AС1 и плоскостью BСC1.

Решение.
Из точки А опускаем перпендикуляр.
Т.к. , , то и
Тогда AC1 – наклонная, ВС1– проекция прямой AC1 на плоскость BСC1. Т.к. угол между прямой и плоскостью – это угол между этой прямой и её проекцией на плоскость, то – искомый.
Треугольник ABC1- прямоугольный.
.
Пусть сторона куба равна a. Тогда .
.
Ответ: .
2.Сторона основания правильной призмы ABCDA1B1C1D1 равна 12, а боковое ребро.Найдите градусную меру угла между плоскостями AB1C и ABC.

Решение.
Плоскость AB1C пересекает плоскость ABC по прямой AC. Построим линейный угол двугранного угла между этими плоскостями.
Для этого из точки B проведём перпендикуляр к прямой AC. Т.к. призма правильная, то её основанием является правильный четырёхугольник – квадрат. Диагонали квадрата взаимно перпендикулярны, следовательно, искомый перпендикуляр-отрезок BO – половина диагонали BD, причём точка O – середина отрезка AC.
Т.к. призма правильная, то она прямая, значит, боковые рёбра перпендикулярны плоскости основания. Следовательно, BO – проекция наклонной B1O. По теореме о трёх перпендикулярах наклонная B1O перпендикулярна прямой AC.
Следовательно, угол BOB1 является линейным углом двугранного угла между плоскостями AB1C и ABC.
В квадрате ABCD AB=12, BD=, BO=:2 =
Рассмотрим треугольник BB1O.
, а значит, прямая BB1 перпендикулярна любой прямой, лежащей в плоскости ABC. Поэтому треугольник OBB1 -прямоугольный, а значит
, следовательно, .
Ответ: 300.
3. В прямоугольном параллелепипеде АВСДА1В1С1Д1найдите угол между плоскостью АА1С и прямой А1В, если АА1=3, АВ=4, ВС= 4.
Решение. Из точки В проведем перпендикуляр ВН к АС. А1Н – проекция А1В на плоскость АА1С. Значит, угол ВА1Н- искомый.
Из прямоугольного треугольника АВС находим ВН=2.
Из прямоугольного треугольника А1АВ находим А1В= 5.
Из прямоугольного треугольника А1НВ находим sinА1==

Ответ: arcsin.
Задачи для самостоятельного решения.
1. Объём прямоугольного параллелепипеда равен 32. Чему будет равен объём
параллелепипеда, если каждое его ребро уменьшить в 2 раза. (4)
2. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 36 см. На какой высоте будет находиться уровень воды, если её перелить в другой сосуд той же формы, у которого сторона основания в 3 раза больше, чем у первого. Ответ выразите в сантиметрах. (4)
3. Закрытый сосуд в виде прямоугольного параллелепипеда с ребрами 30, 40 и 45 см. стоит на горизонтальной поверхности таким образом, что наименьшая грань является дном. В сосуд налили воду до уровня 36 см. На каком уровне окажется вода, если сосуд поставить на наибольшую грань? Ответ дайте в сантиметрах. ( 24 )
4. В кубе ABCDA1B1C1D1 найдите тангенс угла между прямой AA1 и плоскостью BC1D. ()
5. Основание прямой призмы АВСА1В1С1- треугольник АВС, в котором, ВС=2, sinА=0,3. Высота призмы равна. Найдите синус угла между прямой ВС1 и плоскостью АСС1. ( 0,2)
6. В основании прямой призмы лежит равнобедренный треугольник с основанием, равным 6 см., и углом при вершине 120º. Диагональ боковой грани, содержащей основание равнобедренного треугольника, равна 10 см. Найдите площадь боковой поверхности. (48 +32)
Источник
8. Геометрия в пространстве (стереометрия)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
(blacktriangleright) Прямоугольный параллелепипед – это параллелепипед, все грани которого являются прямоугольниками.
Другими словами, это прямая призма, основания которой – прямоугольники.
(эти определения эквивалентны).
Тогда:
1) противоположные грани равны между собой;
2) боковые ребра перпендикулярны основаниям, то есть являются высотами;
3) как следствие, формула для объема принимает вид: ({Large{V=abc}}), где (a, b, c) – три различных боковых ребра.
(blacktriangleright) Диагональ прямоугольного параллелепипеда – это отрезок, соединяющий две противоположные (не лежащие в одной грани) вершины.
1) Все диагонали равны, пересекаются в одной точке и делятся ею пополам;
2) Диагональ (d) можно найти по формуле: ({Large{d^{,2}=a^2+b^2+c^2}}).
Задание
1
#2863
Уровень задания: Легче ЕГЭ
Дан прямоугольный параллелепипед, стороны основания которого равны (4) и (5), а боковое ребро равно (3). Найдите наибольшую площадь его грани.
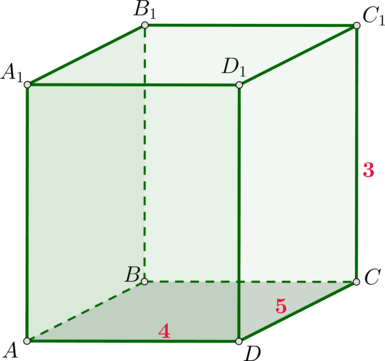
Заметим, что все варианты для площадей его граней – это всевозможные попарные произведения чисел (3,4,5), то есть (3cdot
4), (4cdot 5) или (3cdot 5). Среди этих произведений наибольшим является (4cdot 5=20).
Ответ: 20
Задание
2
#2864
Уровень задания: Легче ЕГЭ
Даны два прямоугольных параллелепипеда: ребра одного равны (185), (185) и (37); а ребра другого равны (185, 37) и (37). Во сколько раз объем первого параллелепипеда больше объема второго параллелепипеда?
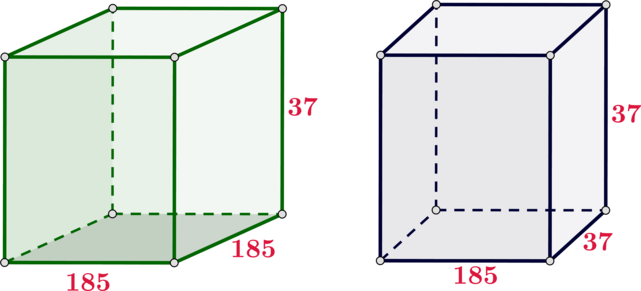
Отношение их объемов равно: [dfrac{V_1}{V_2}=dfrac{185cdot 185cdot 37}{185cdot 37cdot 37}=
dfrac{185}{37}=5.]
Ответ: 5
Задание
3
#2865
Уровень задания: Легче ЕГЭ
Даны два прямоугольных параллелепипеда: ребра одного равны (a, b) и (b), а ребра другого равны (a, a) и (b). На сколько площадь полной поверхности первого параллелепипеда больше, чем площадь поверхности второго параллелепипеда, если (a=1000, b=1001).
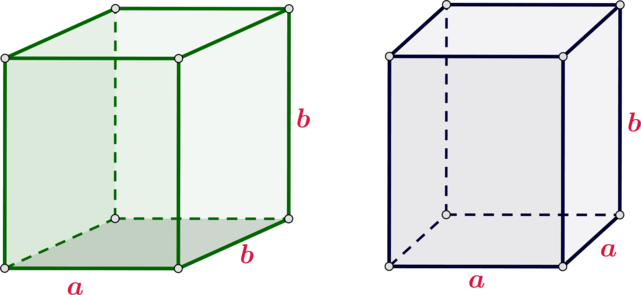
Площадь полной поверхности первого параллелепипеда [S_1=2(ab+b^2+ab)] Площадь полной поверхности второго параллелепипеда [S_2=2(ab+ab+a^2)] Следовательно, [S_1-S_2=2(b^2-a^2)=2(b-a)(b+a)=2(1001-1000)(1001+1000)=4002.]
Ответ: 4002
Дан прямоугольный параллелепипед (ABCDA_1B_1C_1D_1). Во сколько раз объем пирамиды (AA_1BD) меньше объема этого параллелепипеда?
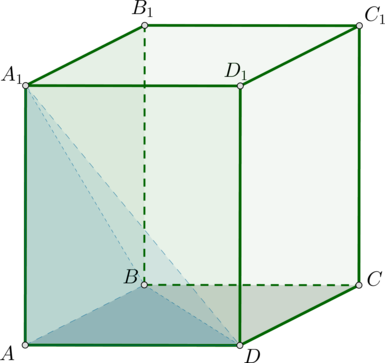
Пусть (AB=x), (AD=y), (AA_1=z). Тогда объем параллелепипеда равен [V_{par}=S_{ABCD}cdot AA_1=xycdot z.] Так как (S_{ABD}=0,5S_{ABCD}) (потому что по определению прямоугольного параллелепипеда в основании лежит прямоугольник), то объем пирамиды [V_{pir}=dfrac13cdot S_{ABC}cdot AA_1=
dfrac13cdot dfrac12xycdot z=dfrac16xyz.] Следовательно, объем пирамиды в 6 раз меньше объема параллелепипеда.
Ответ:
6
Задание
5
#2867
Уровень задания: Равен ЕГЭ
В прямоугольном параллелепипеде диагональ грани (AA_1D_1D) равна (5), а (AB=2sqrt6). Найдите диагональ параллелепипеда.
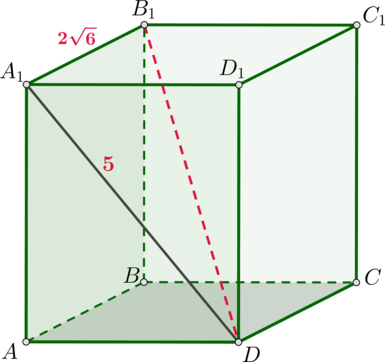
Так как параллелепипед прямоугольный, то все его грани – прямоугольники, а у прямоугольника обе диагонали равны. Следовательно, (A_1D=AD_1). Рассмотрим диагональ (A_1D) и диагональ параллелепипеда (B_1D). Треугольник (A_1B_1D) прямоугольный, так как ребро (A_1B_1) перпендикулярно грани (AA_1D_1D) (по определению прямоугольного параллелепипеда). Следовательно, гипотенуза [B_1D=sqrt{A_1B_1^2+A_1D^2}=sqrt{5^2+(2sqrt6)^2}=7.]
Ответ: 7
Задание
6
#2641
Уровень задания: Равен ЕГЭ
Дан прямоугольный параллелепипед с ребрами (2, 3) и (6). Найдите его диагональ.
Пусть (AB=2, AD=3 , AA_1=6).
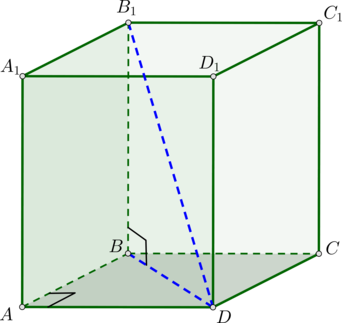
По теореме Пифагора из прямоугольного треугольника (ABD) ((angle
A=90^circ)) имеем: (BD^2=AB^2+AD^2).
Из прямоугольного треугольника (BB_1D) ((angle B=90^circ)) по теореме Пифагора (B_1D^2=BD^2+BB_1^2).
Подставляя (BD^2) из первого равенства во второе, получим:
[B_1D^2=AB^2+AD^2+BB_1^2=2^2+3^2+6^2=4+9+36=49 quad Leftrightarrow quad B_1D=7.]
Ответ: 7
Задание
7
#2689
Уровень задания: Равен ЕГЭ
Найдите объём фигуры, получившейся после удаления маленького прямоугольного параллелепипеда из большого.
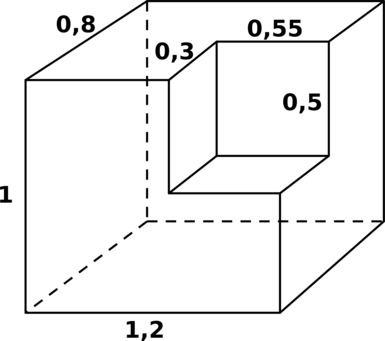
Объём оставшейся фигуры равен разности объёмов большого прямоугольного параллелепипеда (каким он был до удаления) и маленького (удалённого).
Таким образом, искомый объём равен [0,8cdot 1cdot 1,2 – 0,3cdot 0,5cdot 0,55 = 0,8775,.]
Ответ: 0,8775
Учащимся старших классов будет полезно научиться решать задачи ЕГЭ на нахождение объема и других неизвестных параметров прямоугольного параллелепипеда. Опыт предыдущих лет подтверждает тот факт, что подобные задания являются для многих выпускников достаточно сложными.
При этом понимать, как найти объем или площадь прямоугольного параллелепипеда, должны старшеклассники с любым уровнем подготовки. Только в этом случае они смогут рассчитывать на получение конкурентных баллов по итогам сдачи единого госэкзамена по математике.
Основные нюансы, которые стоит запомнить
- Параллелограммы, из которых состоит параллелепипед, являются его гранями, их стороны — ребрами. Вершины этих фигур считаются вершинами самого многогранника.
- Все диагонали прямоугольного параллелепипеда равны. Так как это прямой многогранник, то боковые грани представляют собой прямоугольники.
- Так как параллелепипед — это призма, в основании которой находится параллелограмм, эта фигура обладает всеми свойствами призмы.
- Боковые ребра прямоугольного параллелепипеда перпендикулярны основанию. Следовательно, они являются его высотами.
Готовьтесь к ЕГЭ вместе со «Школково»!
Чтобы занятия проходили легко и максимально эффективно, выбирайте наш математический портал. Здесь вы найдете весь необходимый материал, который потребуется на этапе подготовки к единому государственному экзамену.
Специалисты образовательного проекта «Школково» предлагают пойти от простого к сложному: сначала мы даем теорию, основные формулы и элементарные задачи с решением, а затем постепенно переходим к заданиям экспертного уровня. Вы можете потренироваться, например, с решением задач на тему “Призма”.
Нужную базовую информацию вы найдете в разделе «Теоретическая справка». Вы также можете сразу приступить к решению задач по теме «Прямоугольный параллелепипед» в онлайн-режиме. В разделе «Каталог» представлена большая подборка упражнений разной степени сложности. База заданий регулярно пополняется.
Проверьте, легко ли вы сможете найти объем прямоугольного параллелепипеда, прямо сейчас. Разберите любое задание. Если упражнение дается вам легко, переходите к более сложным задачам. А если возникли определенные сложности, рекомендуем вам планировать свой день таким образом, чтобы ваше расписание включало занятия с дистанционным порталом «Школково».
Источник
