Закрытый сосуд виде прямоугольного параллелепипеда
Что такое параллелепипед?
Что за слово такое мудреное – «параллелепипед»?
Что за многогранник скрывается за этим словом?
Что-то должно быть связано с параллельностью, не правда ли?
Так и есть. Смотри один из вебинаров нашей Программы подготовки к профильному ЕГЭ по математике, читай статью и ты все поймешь!
Куб, параллелепипед. Видео (1 час 53 минуты)
Это видео – один из вебинаров нашей Программы подготовки к профильному ЕГЭ по математике. Вся программа – это:
- 3 вебинара в неделю c Алексеем Шевчуком до самой даты экзамена;
- проверка домашних работ по каждому вебинару;
- майский марафон “Год за месяц”, где мы повторим все темы ЕГЭ, то есть “упакуем” ваши знания, чтобы получить максимум на ЕГЭ.
Выбирай нужную программу и приходи на вебинары:
- “75+ баллов” – для тех, кто “ничего не знает”, но хочет успеть подготовиться к ЕГЭ на 75 баллов;
- “90+ баллов” – для продвинутых, кому нужно 90+ баллов на ЕГЭ. Простые темы мы изучать не будем;
- “Все включено” – включает в себя все, что входит в программы “75+ баллов” и “90+”. Доступ к программе дается на 2 года, поэтому она прекрасно подходит для 10-классников, а так же для тех, кому надо с нуля добраться до 90+ баллов за оставшееся время.
Параллелепипед – многоугольник, образованный пересечением трех пар параллельных плоскостей.
Если слишком сложно, просто посмотри на картинку.
Какую фигуру из планиметрии (геометрии с «плоскими» фигурами) напоминает параллелепипед?
Немного похоже на параллелограмм, правда? Только «потолще» и слово подлиннее.
Смотри, запоминай и не путай!
Высота – перпендикуляр, опущенный из любой вершины параллелепипеда на противоположную грань.
Та грань, на которую опущена высота, называется основанием.
- Все грани параллелепипеда – параллелограммы.
- Противоположные грани параллелепипеда параллельны и равны.
Внимание: передняя и задняя грани параллелепипеда равны, верхняя и нижняя – тоже равны, но не равны (не обязаны быть равны) передняя и верхняя грани – потому что они не противоположные, асмежные.
- Боковые ребра параллелепипеда равны.
- Диагонали параллелепипеда пересекаются и точкой пересечения делятся пополам.
Точка пересечения диагоналей называется центром параллелепипеда.
Прямым называется параллелепипед, у которого боковые ребра перпендикулярны основанию.
Вот так:
У прямого параллелепипеда в основании – параллелограмм, а боковые грани – прямоугольники.
Прямоугольным называется параллелепипед, у которого в основании прямоугольник, а боковые ребра перпендикулярны основанию.
Это такая обувная коробка:
У прямоугольного параллелепипеда все грани – прямоугольники.
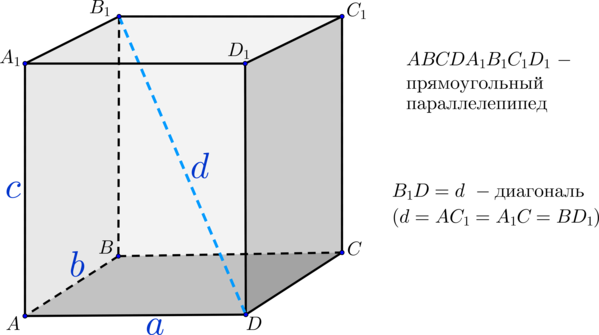
Давай-ка теперь выведем одну интересную формулу для диагонали прямоугольного параллелепипеда.
Диагональ прямоугольного параллелепипеда равна сумме квадратов его измерений.
( displaystyle {{d}^{2}}={{a}^{2}}+{{b}^{2}}+{{c}^{2}}).
Видишь, как красиво? На теорему Пифагора похоже, правда? И формула эта как раз и получается из теоремы Пифагора.
Смотри:
( displaystyle Delta BAD) – прямоугольный, поэтому
( displaystyle B{{D}^{2}}=A{{B}^{2}}+A{{D}^{2}}={{b}^{2}}+{{c}^{2}})
( displaystyle Delta BD{{D}_{1}}) – тоже прямоугольный!
Поэтому
( displaystyle B{{D}_{1}}^{2}=B{{D}^{2}}+D{{D}_{1}}^{2}),
Подставим:
( displaystyle {{d}^{2}}={{a}^{2}}+{{b}^{2}}+{{c}^{2}})
Вывели формулу.
Куб – параллелепипед, у которого все грани квадраты.
Все ребра куба равны.
Кстати, заметь, что куб – частный вид прямоугольного параллелепипеда.
Поэтому для диагонали куба действует формула, которую мы получили для прямоугольного параллелепипеда.
( displaystyle {{d}^{2}}={{a}^{2}}+{{a}^{2}}+{{a}^{2}}),
То есть
( displaystyle d=asqrt{3})
Давай убедимся в пользе этой формулы.
Представь, что у тебя задача: «Диагональ куба равна ( displaystyle 5sqrt{3}). Найти полную поверхность».
Решим ее.
Этот контент доступен после регистрации
Вы также получите доступ к 15 статьям YouClever без ограничений, видеоурокам и другим бесплатным материалам по тарифу “Репетитор”.
Пользуясь нашей формулой: ( displaystyle d=asqrt{3}), мы узнали, что ( displaystyle 5sqrt{3}=asqrt{3} ), то есть ( displaystyle a=5).
Значит полная поверхность – шесть площадей квадратов со стороной ( displaystyle a) -равна:
( displaystyle S=6cdot {{a}^{2}}=6cdot 25=150).
Видишь, как быстро? И ты применяй!
Определения:
Параллелепипед — это четырехугольная призма (многогранник с ( displaystyle 6) гранями), все грани которой — параллелограммы.
Прямой параллелепипед — это параллелепипед, у которого ( displaystyle 4) боковые грани — прямоугольники.
Прямоугольный параллелепипед — параллелепипед, у которого все грани – прямоугольники
Куб — параллелепипед, у которого все грани квадраты.
Высота параллелепипеда – перпендикуляр, опущенный из любой вершины параллелепипеда на противоположную грань.
Свойства:
- Противолежащие грани параллелепипеда параллельны и равны.
- Диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам.
- Любой отрезок с концами, принадлежащими поверхности параллелепипеда и проходящий через точку пересечения диагоналей (центр параллелепипеда), делится ею пополам.
- Все диагонали прямоугольного параллелепипеда равны между собой и равны сумме квадратов его измерений.
( displaystyle {{d}^{2}}={{a}^{2}}+{{b}^{2}}+{{c}^{2}}).
P.S. Последний бесценный совет ????
Ну вот, тема закончена. Если ты читаешь эти строки, значит, ты очень крут.
Почему?
Потому что только 5% людей способны освоить что-то самостоятельно. И если ты дочитал до конца, ты попал в эти 5%!
Теперь самое главное.
Ты разобрался с теорией по этой теме. И, повторюсь, это… это просто супер! Ты уже лучше, чем абсолютное большинство твоих сверстников.
Проблема в том, что этого может не хватить…
Для чего?
Для успешной сдачи ОГЭ или ЕГЭ, для поступления в 10 класс или в институт на бюджет и, самое главное, для жизни.
Я не буду тебя ни в чем убеждать, просто скажу одну вещь…
Люди, получившие хорошее образование, зарабатывают намного больше, чем те, кто его не получил. Это статистика.
Но и это не главное.
Главное то, что они более счастливы (есть такие исследования). Возможно, потому, что перед ними открывается гораздо больше возможностей и жизнь становится ярче? Не знаю…
Но думай сам…
Что нужно, чтобы быть наверняка лучше других на ОГЭ или ЕГЭ и быть в конечном итоге… более счастливым?
Набить руку, решая задачи.
На экзамене у тебя не будут спрашивать теорию.
Тебе нужно будет решать задачи на время. И, если ты не решал их (много!), ты обязательно где-нибудь глупо ошибешься или просто не успеешь. Это как в спорте: нужно много раз повторить, чтобы выиграть наверняка.
Найди где хочешь сборник, обязательно с решениями, подробным разбором и решай, решай, решай!
Можешь воспользоваться нашим сборником задач с подробным разбором, и мы их всячески рекомендуем, потому что они разбиты по темам, по типам и даже собраны в целую программу подготовки.
Если решишь набить руку с помощью наших задач, зайди на сайт 100gia и приобрети одну из программ.
А еще можешь зарегистрироваться и получить доступ к огромному количеству бесплатных материалов, видеоуроков, тестов.
После регистрации ты сможешь:
- проверить свою готовность к каждому типу задач на ЕГЭ (пройдя тест);
- подтянуть слабые места с помощью видеоуроков, вебинаров;
- понять тему с помощью статей учебника YouClever;
- набить руку, решая задачи и получая проверку и решения;
- сдать пробный ЕГЭ и получить сразу оценку и разбор ошибок.
Бонус: информатика и физика.
И в заключение…
Если наши задачи тебе не нравятся, найди другие. Только не останавливайся на теории.
“Понял” и “Умею решать” – это совершенно разные навыки. Тебе нужны оба.
Найди задачи и решай!
Время услышать тебя!
Теперь ты знаешь все про параллелепипед и куб. Ты воспользуешься этим в решении многих задач стереометрии!
Считай, ты помог себе из будущего ????
А теперь мы хотим услышать тебя. Напиши в комментариях ниже свое мнение об этой статье!
Помогла ли она тебе? Все ли было понятно?
А еще ты можешь задать любой вопрос. Мы ответим!
Успехов!
Источник
8. Геометрия в пространстве (стереометрия)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
(blacktriangleright) Прямоугольный параллелепипед – это параллелепипед, все грани которого являются прямоугольниками.
Другими словами, это прямая призма, основания которой – прямоугольники.
(эти определения эквивалентны).
Тогда:
1) противоположные грани равны между собой;
2) боковые ребра перпендикулярны основаниям, то есть являются высотами;
3) как следствие, формула для объема принимает вид: ({Large{V=abc}}), где (a, b, c) – три различных боковых ребра.
(blacktriangleright) Диагональ прямоугольного параллелепипеда – это отрезок, соединяющий две противоположные (не лежащие в одной грани) вершины.
1) Все диагонали равны, пересекаются в одной точке и делятся ею пополам;
2) Диагональ (d) можно найти по формуле: ({Large{d^{,2}=a^2+b^2+c^2}}).
Задание
1
#2863
Уровень задания: Легче ЕГЭ
Дан прямоугольный параллелепипед, стороны основания которого равны (4) и (5), а боковое ребро равно (3). Найдите наибольшую площадь его грани.
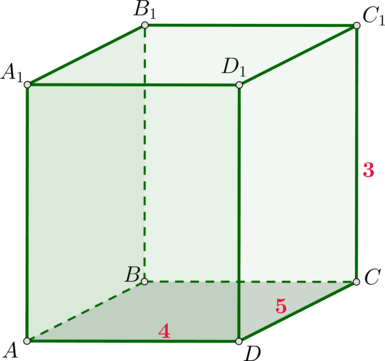
Заметим, что все варианты для площадей его граней – это всевозможные попарные произведения чисел (3,4,5), то есть (3cdot
4), (4cdot 5) или (3cdot 5). Среди этих произведений наибольшим является (4cdot 5=20).
Ответ: 20
Задание
2
#2864
Уровень задания: Легче ЕГЭ
Даны два прямоугольных параллелепипеда: ребра одного равны (185), (185) и (37); а ребра другого равны (185, 37) и (37). Во сколько раз объем первого параллелепипеда больше объема второго параллелепипеда?
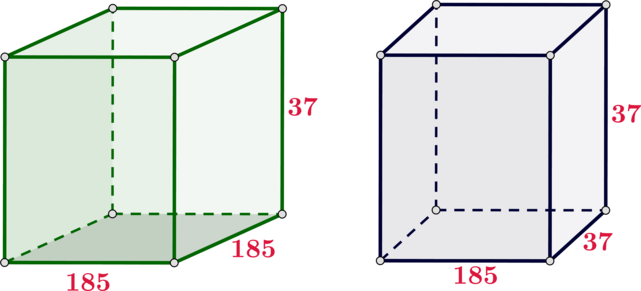
Отношение их объемов равно: [dfrac{V_1}{V_2}=dfrac{185cdot 185cdot 37}{185cdot 37cdot 37}=
dfrac{185}{37}=5.]
Ответ: 5
Задание
3
#2865
Уровень задания: Легче ЕГЭ
Даны два прямоугольных параллелепипеда: ребра одного равны (a, b) и (b), а ребра другого равны (a, a) и (b). На сколько площадь полной поверхности первого параллелепипеда больше, чем площадь поверхности второго параллелепипеда, если (a=1000, b=1001).
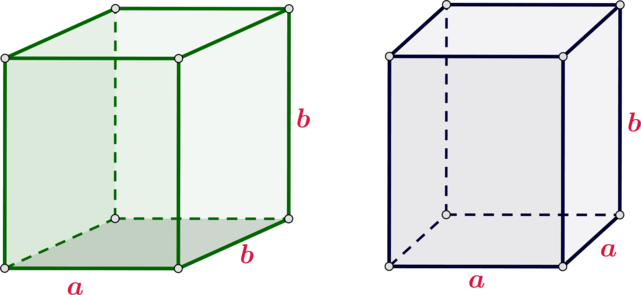
Площадь полной поверхности первого параллелепипеда [S_1=2(ab+b^2+ab)] Площадь полной поверхности второго параллелепипеда [S_2=2(ab+ab+a^2)] Следовательно, [S_1-S_2=2(b^2-a^2)=2(b-a)(b+a)=2(1001-1000)(1001+1000)=4002.]
Ответ: 4002
Задание
4
#3974
Уровень задания: Равен ЕГЭ
Дан прямоугольный параллелепипед (ABCDA_1B_1C_1D_1). Во сколько раз объем пирамиды (AA_1BD) меньше объема этого параллелепипеда?
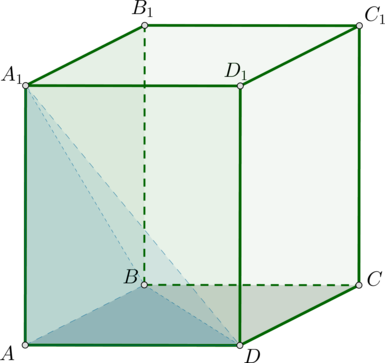
Пусть (AB=x), (AD=y), (AA_1=z). Тогда объем параллелепипеда равен [V_{par}=S_{ABCD}cdot AA_1=xycdot z.] Так как (S_{ABD}=0,5S_{ABCD}) (потому что по определению прямоугольного параллелепипеда в основании лежит прямоугольник), то объем пирамиды [V_{pir}=dfrac13cdot S_{ABC}cdot AA_1=
dfrac13cdot dfrac12xycdot z=dfrac16xyz.] Следовательно, объем пирамиды в 6 раз меньше объема параллелепипеда.
Ответ:
6
Задание
5
#2867
Уровень задания: Равен ЕГЭ
В прямоугольном параллелепипеде диагональ грани (AA_1D_1D) равна (5), а (AB=2sqrt6). Найдите диагональ параллелепипеда.
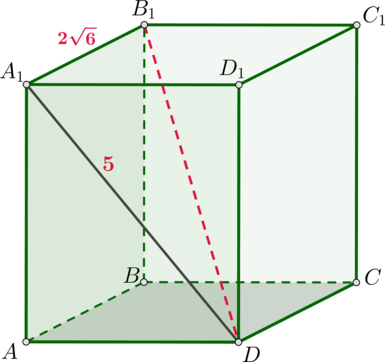
Так как параллелепипед прямоугольный, то все его грани – прямоугольники, а у прямоугольника обе диагонали равны. Следовательно, (A_1D=AD_1). Рассмотрим диагональ (A_1D) и диагональ параллелепипеда (B_1D). Треугольник (A_1B_1D) прямоугольный, так как ребро (A_1B_1) перпендикулярно грани (AA_1D_1D) (по определению прямоугольного параллелепипеда). Следовательно, гипотенуза [B_1D=sqrt{A_1B_1^2+A_1D^2}=sqrt{5^2+(2sqrt6)^2}=7.]
Ответ: 7
Задание
6
#2641
Уровень задания: Равен ЕГЭ
Дан прямоугольный параллелепипед с ребрами (2, 3) и (6). Найдите его диагональ.
Пусть (AB=2, AD=3 , AA_1=6).
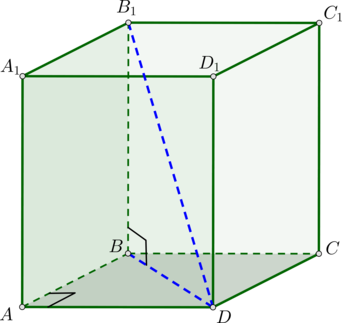
По теореме Пифагора из прямоугольного треугольника (ABD) ((angle
A=90^circ)) имеем: (BD^2=AB^2+AD^2).
Из прямоугольного треугольника (BB_1D) ((angle B=90^circ)) по теореме Пифагора (B_1D^2=BD^2+BB_1^2).
Подставляя (BD^2) из первого равенства во второе, получим:
[B_1D^2=AB^2+AD^2+BB_1^2=2^2+3^2+6^2=4+9+36=49 quad Leftrightarrow quad B_1D=7.]
Ответ: 7
Задание
7
#2689
Уровень задания: Равен ЕГЭ
Найдите объём фигуры, получившейся после удаления маленького прямоугольного параллелепипеда из большого.
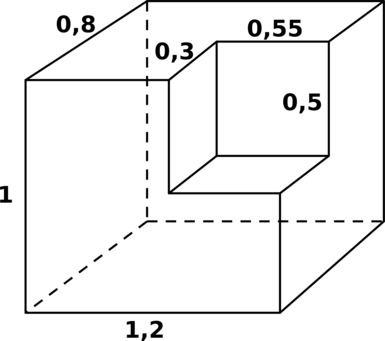
Объём оставшейся фигуры равен разности объёмов большого прямоугольного параллелепипеда (каким он был до удаления) и маленького (удалённого).
Таким образом, искомый объём равен [0,8cdot 1cdot 1,2 – 0,3cdot 0,5cdot 0,55 = 0,8775,.]
Ответ: 0,8775
Учащимся старших классов будет полезно научиться решать задачи ЕГЭ на нахождение объема и других неизвестных параметров прямоугольного параллелепипеда. Опыт предыдущих лет подтверждает тот факт, что подобные задания являются для многих выпускников достаточно сложными.
При этом понимать, как найти объем или площадь прямоугольного параллелепипеда, должны старшеклассники с любым уровнем подготовки. Только в этом случае они смогут рассчитывать на получение конкурентных баллов по итогам сдачи единого госэкзамена по математике.
Основные нюансы, которые стоит запомнить
- Параллелограммы, из которых состоит параллелепипед, являются его гранями, их стороны — ребрами. Вершины этих фигур считаются вершинами самого многогранника.
- Все диагонали прямоугольного параллелепипеда равны. Так как это прямой многогранник, то боковые грани представляют собой прямоугольники.
- Так как параллелепипед — это призма, в основании которой находится параллелограмм, эта фигура обладает всеми свойствами призмы.
- Боковые ребра прямоугольного параллелепипеда перпендикулярны основанию. Следовательно, они являются его высотами.
Готовьтесь к ЕГЭ вместе со «Школково»!
Чтобы занятия проходили легко и максимально эффективно, выбирайте наш математический портал. Здесь вы найдете весь необходимый материал, который потребуется на этапе подготовки к единому государственному экзамену.
Специалисты образовательного проекта «Школково» предлагают пойти от простого к сложному: сначала мы даем теорию, основные формулы и элементарные задачи с решением, а затем постепенно переходим к заданиям экспертного уровня. Вы можете потренироваться, например, с решением задач на тему “Призма”.
Нужную базовую информацию вы найдете в разделе «Теоретическая справка». Вы также можете сразу приступить к решению задач по теме «Прямоугольный параллелепипед» в онлайн-режиме. В разделе «Каталог» представлена большая подборка упражнений разной степени сложности. База заданий регулярно пополняется.
Проверьте, легко ли вы сможете найти объем прямоугольного параллелепипеда, прямо сейчас. Разберите любое задание. Если упражнение дается вам легко, переходите к более сложным задачам. А если возникли определенные сложности, рекомендуем вам планировать свой день таким образом, чтобы ваше расписание включало занятия с дистанционным порталом «Школково».
Источник
