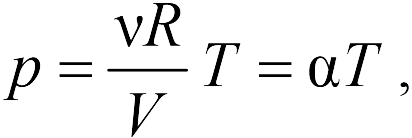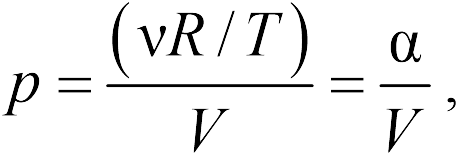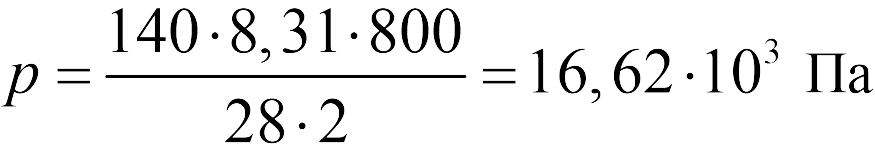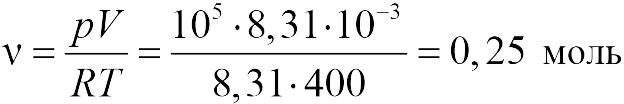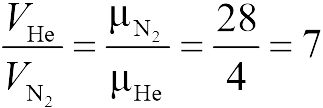Зависимость давления газа от объема сосуда и температуры
В жизни мы встречаем газообразное состояние вещества, когда чувствуем запахи. Запах очень легко распространяется, потому что газ не имеет ни формы, ни объема (он занимает весь предоставленный ему объем), состоит из хаотично движущихся молекул, расстояние между которыми больше, чем размеры молекул.
Агрегатных состояния точно три?
На самом деле, есть еще четвертое – плазма. Звучит, как что-то из научной фантастики, но это просто ионизированный газ – газ, в котором помимо нейтральных частиц, есть еще и заряженные. Ионизаторы воздуха как раз строятся на принципе перехода из газообразного вещества в плазму.
Давление газа
Мы только что выяснили, что молекулы газа беспорядочно движутся. Во время движения они сталкиваются друг с другом, а также со стенками сосуда, в котором этот газ находится. Поскольку молекул много, ударов тоже много.
Например, в комнате, в которой вы сейчас находитесь, на каждый квадратный сантиметр за 1 с молекулами воздуха наносится столько ударов, что их количество выражается двадцати трехзначным числом.
Хотя сила удара отдельной молекулы мала, действие всех молекул о стенки сосуда приводит к значительному давлению. Это как если бы один комар толкал машину, то она бы и не сдвинулась с места, а вот пару сотен миллионов комаров вполне себе способны эту машину сдвинуть.
Зависимость давления от других величин
Зависимость давления от объема
В механике есть формула давления, которая показывает: давление прямо пропорционально силе и обратно пропорционально площади, на которую эта сила оказывается.
Давление
p = F/S
p – давление [Па]
F – сила [Н]
S – площадь [м^2]
То есть, если наши двести миллионов комаров будут толкать легковую машину, они распределятся по меньшей площади, чем если бы они толкали грузовой автомобиль (просто потому что легковая меньше грузовика).
Из формулы давления следует, что давление на легковой автомобиль будет больше из-за меньшей площади.
Давайте рассмотрим аналогичный пример с двумя сосудами разной площади.
Давление в левом сосуде будет больше, чем во втором, по аналогичной схеме – потому что площадь меньше. Но если площадь основания меньше, то и объем меньше. Это значит, что давление будет зависеть от объема следующим образом: чем больше объем, тем меньше давление – и наоборот.
При этом зависимость будет не линейная, а примет вот такой вид (при условии, что температура постоянна):
Такая зависимость называется законом Бойля-Мариотта.
Она экспериментально проверяется с помощью такой установки.
Объем шприца увеличивают с помощью насоса, а манометр измеряет давление. Эксперимент показывает, что при увеличении объема давление действительно уменьшается.
Зависимость давления от температуры
Рассмотрим зависимость давления газа от температуры при условии неизменного объема определенной массы газа. Эти исследования были впервые произведены в Жаком Шарлем.
Газ нагревался в большой колбе, соединенной с ртутным манометром в виде узкой изогнутой трубки. Пренебрегая ничтожным увеличением объема колбы при нагревании и незначительным изменением объема при смещении ртути в узкой манометрической трубке.
Таким образом, можно считать объем газа неизменным. Подогревая воду в сосуде, окружающем колбу, измеряли температуру газа по термометру, а соответствующее давление – по манометру.
Этот эксперимент показал, что давление газа увеличивается с увеличением температуры. Это связано с тем, что при нагревании молекулы газа движутся быстрее, из-за чего чаще ударяются о стенки сосуда.
С температурой все проще. Зависимость давления от температуры при постоянных объеме и массе будет линейно:
Эта зависимость называется законом Шарля.
Хранение и транспортировка газов
Если нужно перевезти значительное количество газа из одного места в другое, или когда газы необходимо длительно хранить – их помещают в специальные прочные металлические сосуды. Из-за того, что при уменьшении объема увеличивается давление, газ можно закачать в небольшой баллон, но он должен быть очень прочным.
Сосуды, предназначенные для транспортировки газов, выдерживают высокие давления. Поэтому с помощью специальных насосов (компрессоров) туда можно закачать значительные массы газа, которые в обычных условиях занимали бы в сотни раз больший объем.
Поскольку давление газов в баллонах даже при комнатной температуре очень велико, их ни в коем случае нельзя нагревать. Например, держать под прямыми лучами солнца или любым способом пытаться сделать в них отверстие, даже после использования.
Понимать и любить этот мир проще, когда разбираешься в физике. В этом помогут небезразличные и компетентные преподаватели онлайн-школы Skysmart.
Чтобы формулы и задачки ожили и стали более дружелюбными, на уроках мы разбираем примеры из обычной жизни современных подростков. Приходите на бесплатный вводный урок по физике и начните учиться в удовольствие уже завтра!
Источник
Задачи на газовые законы часто предлагаются школьникам на едином государственном экзамене. Для решения этих задач вполне достаточно знать уравнение состояния идеального газа (закон Клапейрона-Менделеева) и уметь использовать его алгебраически и геометрически (для построения графиков зависимости одних параметров газа от других) в простейших ситуациях. Кроме того, нужно понимать, как описываются смеси идеальных газов (закон Дальтона).
Уравнение, связывающее параметры газа друг с другом, называется уравнением состояния. Для идеального газа, взаимодействие молекул которого мало, уравнение состояния имеет вид
(13.1) |
где – давление газа, – концентрация молекул газа (число молекул в единице объема), – постоянная Больцмана, – абсолютная (в шкале Кельвина) температура. Учитывая, что , где – число молекул газа, – объем сосуда, в котором находится газ (часто говорят объем газа), получим из (13.1)
(13.2) |
Число молекул можно связать с количеством вещества газа : , где – число Авогадро. Поэтому формулу (13.2) можно переписать в виде
(13.2) |
где произведение постоянных Авогадро и Больцмана обозначено как . Постоянная = 8,31 Дж/(К•моль) называется универсальной газовой постоянной. Количество вещества газа можно также выразить через его массу и молярную массу этого газа
| (13.3) |
С учетом (13.3) закон (13.2) можно переписать и в таком виде
| (13.4) |
Уравнение состояния идеального газа (13.1)-(13.4), которое также называется уравнением (или законом) Клапейрона-Менделеева, позволяет связывать параметры идеального газа и проследить за их изменением в тех или иных процессах.
В школьном курсе физики рассматриваются три изопроцесса, в которых один из трех параметров газа (давление, температура и объем) не изменяется. В изобарическом процессе не изменяется давление газа, в изотермическом – температура, в изохорическом – объем. Изопроцессам отвечают следующие графики зависимости давления от объема, давления от температуры, объема от температуры.
Для изобарического процесса
|
Первые два графика очевидны. Последний получается так. Из закона Клапейрона-Менделеева следует, что зависимость объема от температуры при постоянном давлении имеет вид
| (13.5) |
где – постоянная. Графиком функции (13.5) является прямая, продолжение которой проходит через начало координат.
Для изохорического процесса
|
Второй график следует из соотношения
| (13.6) |
где – постоянная при постоянном объеме.
Для изотермического процесса
|
Первый график следует из закона Клапейрона-Менделеева, который при постоянной температуре газа можно привести к виду
| (13.7) |
где – постоянная. Отсюда следует, что графиком зависимости от в изотермическом процессе является гипербола.
Важнейшее свойство уравнения состояния идеального газа (13.1)-(13.4) заключается в том, что «индивидуальность» газа никак не проявляется в этих законах – единственный параметр собственно газа, входящий в уравнение состояния, – это число молекул. Например, 1 моль гелия и 1 моль азота, находящиеся в одинаковых объемах и имеющие одинаковые температуры, оказывают одинаковое давление. Отсюда следует, что и давление смеси идеальных газов определяется суммарным числом молекул всех компонент смеси:
| (13.8) |
где 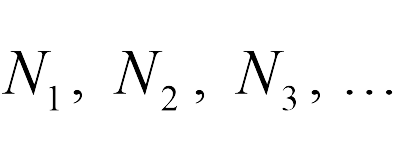 – число молекул первой, второй, третьей и т.д. компонент смеси, – постоянная Больцмана, – абсолютная температура смеси, – объем сосуда. Величины , имеющие смысл давления каждой компоненты смеси при условии, что она имела бы такую же температуру и занимала бы весь объем, называются парциальными давлениями компонент. Закон (13.8) называется законом Дальтона. Рассмотрим теперь в рамках этих законов предложенные выше задачи.
– число молекул первой, второй, третьей и т.д. компонент смеси, – постоянная Больцмана, – абсолютная температура смеси, – объем сосуда. Величины , имеющие смысл давления каждой компоненты смеси при условии, что она имела бы такую же температуру и занимала бы весь объем, называются парциальными давлениями компонент. Закон (13.8) называется законом Дальтона. Рассмотрим теперь в рамках этих законов предложенные выше задачи.
В задаче 13.1.1 из уравнения состояния в форме (13.1), получаем для давления в конце процесса :
т.е. давление газа увеличилось в 6 раз (ответ 1).
Применяя закон Клапейрона-Менделеева (13.2) к первому и второму газам (задача 13.1.2), получаем
где – искомый объем. Сравнивая первую и вторую формулы, заключаем, что (ответ 1).
Закон Клапейрона-Менделеева для газа в начальном и конечном состояниях (задача 13.1.3) дает
где – неизвестная температура. Из сравнения этих формул получаем , т.е. температуру газа в сосуде нужно повысить вдвое (ответ 2).
Из закона Клапейрона-Менделеева для начального и конечного состояний газа в задаче 13.1.4 имеем
Отсюда , т.е. количество вещества газа в сосуде увеличилось в 1,25 раза (ответ 3).
Первым, кто понял, почему жидкость поднимается вместе с трубкой (задача 13.1.5), и почему «природа боится пустоты» (Аристотель), но только до определенного предела, был знаменитый итальянский физик, современник Г. Галилея Э. Торричелли. Давайте рассмотрим рассуждения Торричелли подробно. Основная идея Торричелли заключалась в том, что атмосферный воздух оказывает давление на все поверхности, с которыми он контактирует. В равновесии жидкость занимает такое положение, чтобы все воздействия на каждый ее элемент компенсировались. 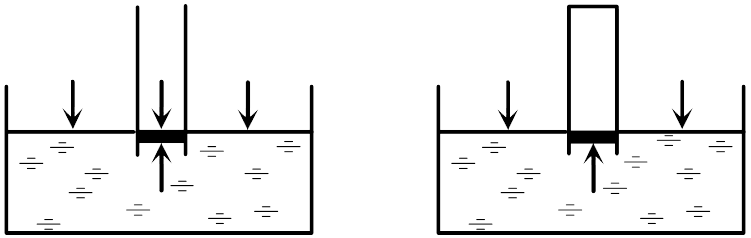 Если бы трубка была открыта (см. левый рисунок), то жидкость не поднялась бы в трубке. Действительно, в этом случае на бесконечно малый элемент жидкости в трубке около поверхности (выделен на рисунке) действовали бы сила со стороны атмосферного воздуха в трубке, направленная вниз. С другой стороны, атмосферный воздух действует и на остальную поверхность жидкости, и это воздействие благодаря закону Паскаля передается выделенному элементу жидкости в трубке снизу. Таким образом, воздействие воздуха на поверхность жидкости в трубке и на свободную поверхность жидкости компенсируют друг друга, если уровень жидкости в трубке совпадает с уровнем жидкости в остальном сосуде. Если же мы поднимаем трубку, выпустив из нее воздух, на рассматриваемый элемент жидкости воздух сверху не действует (его нет в трубке), поэтому воздействие воздуха на свободную поверхность жидкости приведет к тому, что жидкость войдет в трубку и заполнит ее. При вытаскивании трубки жидкость будет подниматься вслед за ней. Однако при дальнейшем поднятии трубки наступит такой момент, когда воздействие воздуха на свободную поверхность и столба жидкости в трубке сравняются (в этот момент атмосферное давление будет равно гидростатическому давлению жидкости в трубке на уровне свободной поверхности). Дальнейший подъем трубки уже не приведет к поднятию жидкости – атмосферное давление не сможет «держать» столб жидкости большей высоты. Для воды этот столб составляет около 10 м, для ртути, с которой и экспериментировал Э. Торричелли, – 76 сантиметров. Таким образом, жидкость в трубке поднимается благодаря давлению атмосферного воздуха на поверхность воды в сосуде и закону Паскаля (ответ 4).
Если бы трубка была открыта (см. левый рисунок), то жидкость не поднялась бы в трубке. Действительно, в этом случае на бесконечно малый элемент жидкости в трубке около поверхности (выделен на рисунке) действовали бы сила со стороны атмосферного воздуха в трубке, направленная вниз. С другой стороны, атмосферный воздух действует и на остальную поверхность жидкости, и это воздействие благодаря закону Паскаля передается выделенному элементу жидкости в трубке снизу. Таким образом, воздействие воздуха на поверхность жидкости в трубке и на свободную поверхность жидкости компенсируют друг друга, если уровень жидкости в трубке совпадает с уровнем жидкости в остальном сосуде. Если же мы поднимаем трубку, выпустив из нее воздух, на рассматриваемый элемент жидкости воздух сверху не действует (его нет в трубке), поэтому воздействие воздуха на свободную поверхность жидкости приведет к тому, что жидкость войдет в трубку и заполнит ее. При вытаскивании трубки жидкость будет подниматься вслед за ней. Однако при дальнейшем поднятии трубки наступит такой момент, когда воздействие воздуха на свободную поверхность и столба жидкости в трубке сравняются (в этот момент атмосферное давление будет равно гидростатическому давлению жидкости в трубке на уровне свободной поверхности). Дальнейший подъем трубки уже не приведет к поднятию жидкости – атмосферное давление не сможет «держать» столб жидкости большей высоты. Для воды этот столб составляет около 10 м, для ртути, с которой и экспериментировал Э. Торричелли, – 76 сантиметров. Таким образом, жидкость в трубке поднимается благодаря давлению атмосферного воздуха на поверхность воды в сосуде и закону Паскаля (ответ 4).
 Сравнивая графики процессов 1, 2, 3 и 4, данные в условии задачи 13.1.6, с графиками изопроцессов, приведенными во введении к настоящей главе, заключаем, что: процесс 1 – изотермический, 2 – изохорический, 3 – изобарический. В процесс 4 меняются и давление, и объем, и температура газа (ответ 4).
Сравнивая графики процессов 1, 2, 3 и 4, данные в условии задачи 13.1.6, с графиками изопроцессов, приведенными во введении к настоящей главе, заключаем, что: процесс 1 – изотермический, 2 – изохорический, 3 – изобарический. В процесс 4 меняются и давление, и объем, и температура газа (ответ 4).
 Изохорическим охлаждением в задаче 13.1.8 является процесс 4 (см. рисунок) В двух последних задачах этого варианта нужно с помощью закона Клапейрона-Менделеева вычислить один из параметров газа, если даны остальные параметры. В задаче 13.1.9 из закона Клапейрона-Менделеева
Изохорическим охлаждением в задаче 13.1.8 является процесс 4 (см. рисунок) В двух последних задачах этого варианта нужно с помощью закона Клапейрона-Менделеева вычислить один из параметров газа, если даны остальные параметры. В задаче 13.1.9 из закона Клапейрона-Менделеева
|
получим
|
(ответ 1).
В задаче 13.1.10 при вычислениях следует не забыть перевести температуру газа в Кельвины. Из закона Клапейрона-Менделеева находим
|
(ответ 1).
Из уравнения состояния в форме (13.2) следует, что при одинаковых объемах и температурах давление идеального газа определяется только полным числом молекул. Поэтому отношение давления водорода и гелия в задаче 13.2.1 равно 2 (ответ 2).
Поскольку перегородка в задаче 13.2.2 подвижная и находится в равновесии, давления газа в отсеках сосуда слева и справа от перегородки равны. Применяя к ним при этом условии закон Клапейрона-Менделеева, получим
для гелия | для азота |
где температуры и массы газов по условию одинаковы. Деля эти уравнения друг на друга, находим отношение объемов частей сосуда
|
(ответ 4).
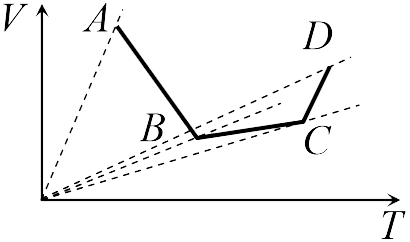
Если бы точки, отвечающие состояниям 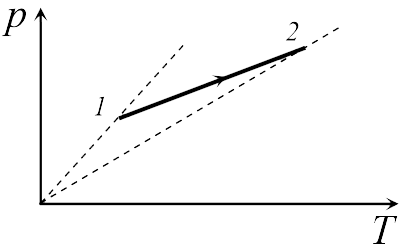 1 и 2 в задаче 13.2.3, лежали на одной прямой, продолжение которой проходит через начало координат, то эти состояния принадлежали бы одной и той же изохоре, и, следовательно, объем газа в этих состояниях был одинаковым (см. формулу (13.6)). Поэтому для сравнения объемов этих состояний построим изохоры, проходящие через точки 1 и 2, и сравним отвечающие им объемы (см. рисунок; изохоры, проходящие через точки 1 и 2, показаны пунктиром).
1 и 2 в задаче 13.2.3, лежали на одной прямой, продолжение которой проходит через начало координат, то эти состояния принадлежали бы одной и той же изохоре, и, следовательно, объем газа в этих состояниях был одинаковым (см. формулу (13.6)). Поэтому для сравнения объемов этих состояний построим изохоры, проходящие через точки 1 и 2, и сравним отвечающие им объемы (см. рисунок; изохоры, проходящие через точки 1 и 2, показаны пунктиром).
Из формулы (13.6) следует, что чем больше объем, тем меньше коэффициент перед в зависимости (13.6), и, следовательно, меньше наклон соответствующей изохоры к оси температур. Поэтому изохоре 1 отвечает больший объем, чем изохоре 2, и, следовательно, объем газа в процессе 1-2 уменьшается (ответ 2).
Аналогичные рассуждения в задаче 13.2.4 показывают, что наибольшему давлению отвечает изобара, проходящая через точку (поскольку соответствующая прямая имеет наименьший наклон к оси температур; см. рисунок ниже). Поэтому правильный ответ в этой задаче – 3.
|
В закон Клапейрона-Менделеева входит абсолютная температура газа, поэтому данные в задаче 13.2.5 значения нужно перевести в Кельвины. В результате для отношения давлений газа в конечном и начальном состояниях получаем
|
(ответ 4).
Как следует из опыта, при приведении тел в тепловой контакт выравниваются их температуры. Это же касается и частей одного тела или даже компонент смеси газов (задача 13.2.6). Поэтому температуры компонент смеси будут одинаковы (ответ 1). Что касается парциальных давлений, плотностей или концентрации компонент смеси, то их значения зависят от количества молекул каждой компоненты смеси и могут быть различны.
Парциальное давление компонент смеси – это давление, которое оказывают только молекулы каждой компоненты. Как следует из формулы (13.8) парциальное давление любой компоненты можно найти, применяя только к ней закон Клапейрона-Менделеева и считая, что она имеет такую же температуру, как и вся смесь, и занимает такай же объем, как и вся смесь газов. Поэтому отношение парциальных давлений отдельных компонент смеси равно отношению количеств вещества (или числа молекул) этих компонент. Поэтому для отношения парциальных давлений углекислого газа и гелия в сосуде в задаче 13.2.7 имеем (ответ 2).
Как следует из закона Дальтона, давление смеси газов определяется полным количеством молекул в ней. Поэтому для анализа изменения давления смеси газов при протекании в ней химической реакции (задача 13.2.8) необходимо исследовать изменение числа молекул. Гелий не участвует в химической реакции – один моль гелия был и в начальном, и в конечном состоянии смеси. С озоном происходила реакция
т.е. из двух молекул озона в результате реакции получились три молекулы кислорода. Поэтому два моля озона превратились в три моля кислорода, и общее количество вещества смеси стало равно четырем молям. Поэтому давление смеси увеличивается в 4/3 раза (ответ 2).
Поскольку объемы и температуры газов одинаковы (задача 13.2.9), для сравнения их давлений необходимо сравнить число молекул в них. По условию в одном сосуде находится один моль азота, в другом 1 г водорода (т.е. половина моля) и 3 • 1023 молекул гелия (тоже половина моля). Поэтому и в одном и в другом сосуде находятся одинаковые количества молекул, и, следовательно, давление газов в них одинаково (ответ 3).
Плотность газа (задача 13.2.10) можно найти из следующей цепочки формул
|
(ответ 4). Здесь – масса газа, – масса одной молекулы газа.
Источник
Убедимся в том, что молекулы газа действительно расположены достаточно далеко друг от друга, и поэтому газы хорошо сжимаемы.Возьмем шприц и расположим его поршень приблизительно посередине цилиндра. Отверстие шприца соединим с трубкой, второй конец которой наглухо закрыт. Таким образом, некоторая порция воздуха будет заключена в цилиндре шприца под поршнем и в трубке.В цилиндре под поршнем заключено некоторое количество воздуха. Теперь поставим на подвижный поршень шприца груз. Легко заметить, что поршень немного опустится. Это означает, что объем воздуха уменьшился Другими словами, газы легко сжимаются. Таким образом, между молекулами газа имеются достаточно большие промежутки. Помещение груза на поршень вызывает уменьшение объема газа. С другой стороны, после установки груза поршень, немного опустившись, останавливается в новом положении равновесия. Это означает, что сила давления воздуха на поршень увеличивается и снова уравновешивает возросший вес поршня с грузом . А поскольку площадь поршня при этом остается неизменной, мы приходим к важному заключению.
При уменьшении объема газа его давление увеличивается.
Будем помнить при этом, что масса газа и его температура в ходе опыта оставались неизменными. Объяснить зависимость давления от объема можно следующим образом. При увеличении объема газа расстояние между его молекулами увеличивается. Каждой молекуле теперь нужно пройти большее расстояние от одного удара со стенкой сосуда до другого. Средняя скорость движения молекул остается неизменной .Следовательно, молекулы газа реже ударяются о стенки сосуда, а это приводит к уменьшению давления газа. И, наоборот, при уменьшении объема газа его молекулы чаще ударяются о стенки сосуда, и давление газа увеличивается . При уменьшении объема газа расстояние между его молекулами уменьшается
Зависимость давления газа от температуры
В предыдущих опытах температура газа оставалась неизменной, и мы изучали изменение давления вследствие изменения объема газа. Теперь рассмотрим случай, когда объем газа остается постоянным, а температура газа изменяется. Масса при этом также остается неизменной. Создать такие условия можно, поместив некоторое количество газа в цилиндр с поршнем и закрепив поршень
Изменение температуры данной массы газа при неизменном объеме
Чем выше температура, тем быстрее движутся молекулы газа.
Следовательно,
– во-первых, чаще происходят удары молекул о стенки сосуда;
– во-вторых, средняя сила удара каждой молекулы о стенку становится больше. Это приводит нас к еще одному важному заключению. При увеличении температуры газа его давление увеличивается. Будем помнить, что данное утверждение справедливо, если масса и объем газа в ходе изменения его температуры остаются неизменными.
Хранение и транспортировка газов.
Зависимость давления газа от объема и температуры часто используется в технике и в быту. Если требуется перевезти значительное количество газа из одного места в другое, или когда газы необходимо длительно хранить, их помещают в специальные прочные металлические сосуды. Эти сосуды выдерживают высокие давления, поэтому с помощью специальных насосов туда можно закачать значительные массы газа, которые в обычных условиях занимали бы в сотни раз больший объем. Поскольку давление газов в баллонах даже при комнатной температуре очень велико, их ни в коем случае нельзя нагревать или любым способом пытаться сделать в них отверстие даже после использования.
Газовые законы физики.
Физика реального мира в расчетах часто сводится к несколько упрощенным моделям. Наиболее применим такой подход к описанию поведения газов. Правила, установленные экспериментальным путем, были сведены различными исследователями в газовые законы физики и послужили появлению понятия «изопроцесс». Это такое прохождение эксперимента, при котором один параметр сохраняет постоянное значение. Газовые законы физики оперируют основными параметрами газа, точнее, его физического состояния. Температурой, занимаемым объемом и давлением. Все процессы, которые относятся к изменению одного или нескольких параметров и называются термодинамическими. Понятие изостатического процесса сводится к утверждению, что во время любого изменения состояния один из параметров остается неизменным. Это поведение так называемого «идеального газа», которое, с некоторыми оговорками, может быть применено к реальному веществу. Как отмечено выше, в реальности все несколько сложнее. Однако, с высокой достоверностью поведение газа при неизменной температуре характеризуется с помощью закона Бойля-Мариотта, который гласит:
Произведение объема на давление газа – величина постоянная. Это утверждение считается верным в том случае, когда температура не изменяется.
Этот процесс носит название «изотермический». При этом меняются два из трех исследуемых параметров. Физически все выглядит просто. Сожмите надутый шарик. Температуру можно считать неизменной. А в результате внутри шара повысится давление при уменьшении объема. Величина произведения двух параметров останется неизменной. Зная исходное значение хотя бы одного из них, можно легко узнать показатели второго. Еще одно правило в списке «газовые законы физики» – изменение объема газа и его температуры при одинаковом давлении. Это называется «изобарный процесс» и описывается с помощью закона Гей-Люсака. Соотношение объема и температуры газа неизменно. Это верно при условии постоянного значения давления в данной массе вещества. Физически тоже все просто. Если хоть раз заряжали газовую зажигалку или пользовались углекислотным огнетушителем, видели действие этого закона «вживую». Газ, выходящий из баллончика или раструба огнетушителя, быстро расширяется. Его температура резко падает. Можно обморозить кожу рук. В случае с огнетушителем – образуются целые хлопья углекислотного снега, когда газ под воздействием низкой температуры быстро переходит в твердое состояние из газообразного. Благодаря закону Гей-Люсака, можно легко узнать температуру газа, зная его объем в любой момент времени. Газовые законы физики описывают и поведение при условии неизменного занимаемого объема. Такой процесс называется изохорным и описывается законом Шарля, который гласит: При неизменном занимаемом объеме, отношение давления к температуре газа остается неизменным в любой момент времени.В реальности все знают правило: нельзя нагревать баллончики от освежителей воздуха и прочие сосуды, содержащие газ под давлением. Дело кончается взрывом. Происходит именно то, что описывает закон Шарля. Растет температура. Одновременно растет давление, так как объем не меняется. Происходит разрушение баллона в момент, когда показатели превышают допустимые. Так что, зная занимаемый объем и один из параметров, можно легко установить значение второго. Хотя газовые законы физики описывают поведение некой идеальной модели, их можно легко применять для предсказания поведения газа в реальных системах. Особенно в быту, изопроцессы могут легко объяснить, как работает холодильник, почему из баллончика освежителя вылетает холодная струя воздуха, из-за чего лопается камера или шарик, как работает разбрызгиватель и так далее.
Основы МКТ.
Молекулярно-кинетическая теория вещества- способ объяснения тепловых явлений, который связывает протекание тепловых явлений и процессов с особенностями внутреннего строения вещества и изучает причины, которые обусловливают тепловое движение. Эта теория получила признание лишь в XX в., хотя исходит из древнегреческого атомного учения о строении вещества.
Молекулярно-кинетическая теория объясняет тепловые явления особенностями движения и взаимодействия микрочастиц вещества
Молекулярно-кинетическая теория основывается на законах классической механики И. Ньютона, которые позволяют вывести уравнение движения микрочастиц. Тем не менее в связи с огромным их количеством (в 1 см3 вещества находится около 1023 молекул) невозможно ежесекундно с помощью законов классической механики однозначно описать движение каждой молекулы или атома. Поэтому для построения современной теории теплоты используют методы математической статистики, которые объясняют течение тепловых явлений на основании закономерностей поведения значительного количества микрочастиц.
Молекулярно-кинетическая теория построена на основании обобщенных уравнений движения огромного количества молекул.
Молекулярно-кинетическая теория объясняет тепловые явления с позиций представлений о внутреннем строении вещества, то есть выясняет их природу. Это более глубокая, хотя и более сложная теория, которая объясняет сущность тепловых явлений и обусловливает законы термодинамики.
Оба существующих подхода – термодинамический подход и молекулярно-кинетическая теория – научно доказаны и взаимно дополняют друг друга, а не противоречат друг другу. В связи с этим изучение тепловых явлений и процессов обычно рассматривается с позиций или молекулярной физики, или термодинамики, в зависимости от того, как проще изложить материал.
Термодинамический и молекулярно-кинетический подходы взаимно дополняют друг друга при объяснении тепловых явлений и процессов.
Источник