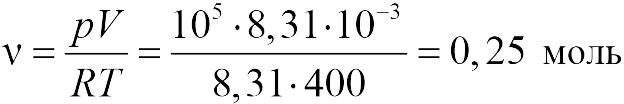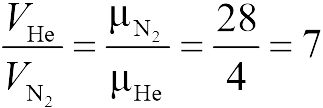Зависимость давления газа в сосуде от температуры
Задачи на газовые законы часто предлагаются школьникам на едином государственном экзамене. Для решения этих задач вполне достаточно знать уравнение состояния идеального газа (закон Клапейрона-Менделеева) и уметь использовать его алгебраически и геометрически (для построения графиков зависимости одних параметров газа от других) в простейших ситуациях. Кроме того, нужно понимать, как описываются смеси идеальных газов (закон Дальтона).
Уравнение, связывающее параметры газа друг с другом, называется уравнением состояния. Для идеального газа, взаимодействие молекул которого мало, уравнение состояния имеет вид
| (13.1) |
где 
— давление газа, 
— концентрация молекул газа (число молекул в единице объема), 
— постоянная Больцмана, 
— абсолютная (в шкале Кельвина) температура. Учитывая, что 
, где 
— число молекул газа, 
— объем сосуда, в котором находится газ (часто говорят объем газа), получим из (13.1)
| (13.2) |
Число молекул 
можно связать с количеством вещества газа 
: 
, где 
— число Авогадро. Поэтому формулу (13.2) можно переписать в виде
| (13.2) |
где произведение постоянных Авогадро и Больцмана обозначено как 
. Постоянная 
= 8,31 Дж/(К•моль) называется универсальной газовой постоянной. Количество вещества газа можно также выразить через его массу 
и молярную массу этого газа 
| (13.3) |
С учетом (13.3) закон (13.2) можно переписать и в таком виде
| (13.4) |
Уравнение состояния идеального газа (13.1)-(13.4), которое также называется уравнением (или законом) Клапейрона-Менделеева, позволяет связывать параметры идеального газа и проследить за их изменением в тех или иных процессах.
В школьном курсе физики рассматриваются три изопроцесса, в которых один из трех параметров газа (давление, температура и объем) не изменяется. В изобарическом процессе не изменяется давление газа, в изотермическом — температура, в изохорическом — объем. Изопроцессам отвечают следующие графики зависимости давления от объема, давления от температуры, объема от температуры.
Для изобарического процесса
|
Первые два графика очевидны. Последний получается так. Из закона Клапейрона-Менделеева следует, что зависимость объема от температуры при постоянном давлении имеет вид
| (13.5) |
где 
— постоянная. Графиком функции (13.5) является прямая, продолжение которой проходит через начало координат.
Для изохорического процесса
|
Второй график следует из соотношения
| (13.6) |
где 
— постоянная при постоянном объеме.
Для изотермического процесса
|
Первый график следует из закона Клапейрона-Менделеева, который при постоянной температуре газа можно привести к виду
| (13.7) |
где 
— постоянная. Отсюда следует, что графиком зависимости 
от 
в изотермическом процессе является гипербола.
Важнейшее свойство уравнения состояния идеального газа (13.1)-(13.4) заключается в том, что «индивидуальность» газа никак не проявляется в этих законах — единственный параметр собственно газа, входящий в уравнение состояния, — это число молекул. Например, 1 моль гелия и 1 моль азота, находящиеся в одинаковых объемах и имеющие одинаковые температуры, оказывают одинаковое давление. Отсюда следует, что и давление смеси идеальных газов 
определяется суммарным числом молекул всех компонент смеси:
| (13.8) |
где 
— число молекул первой, второй, третьей и т.д. компонент смеси, 
— постоянная Больцмана, 
— абсолютная температура смеси, 
— объем сосуда. Величины 
, имеющие смысл давления каждой компоненты смеси при условии, что она имела бы такую же температуру и занимала бы весь объем, называются парциальными давлениями компонент. Закон (13.8) называется законом Дальтона. Рассмотрим теперь в рамках этих законов предложенные выше задачи.
В задаче 13.1.1 из уравнения состояния в форме (13.1), получаем для давления в конце процесса 
:
|
т.е. давление газа увеличилось в 6 раз (ответ 1).
Применяя закон Клапейрона-Менделеева (13.2) к первому и второму газам (задача 13.1.2), получаем
|
где 
— искомый объем. Сравнивая первую и вторую формулы, заключаем, что 
(ответ 1).
Закон Клапейрона-Менделеева для газа в начальном и конечном состояниях (задача 13.1.3) дает
|
где 
— неизвестная температура. Из сравнения этих формул получаем 
, т.е. температуру газа в сосуде нужно повысить вдвое (ответ 2).
Из закона Клапейрона-Менделеева для начального и конечного состояний газа в задаче 13.1.4 имеем
|
Отсюда 
, т.е. количество вещества газа в сосуде увеличилось в 1,25 раза (ответ 3).
Первым, кто понял, почему жидкость поднимается вместе с трубкой (задача 13.1.5), и почему «природа боится пустоты» (Аристотель), но только до определенного предела, был знаменитый итальянский физик, современник Г. Галилея Э. Торричелли. Давайте рассмотрим рассуждения Торричелли подробно. Основная идея Торричелли заключалась в том, что атмосферный воздух оказывает давление на все поверхности, с которыми он контактирует. В равновесии жидкость занимает такое положение, чтобы все воздействия на каждый ее элемент компенсировались.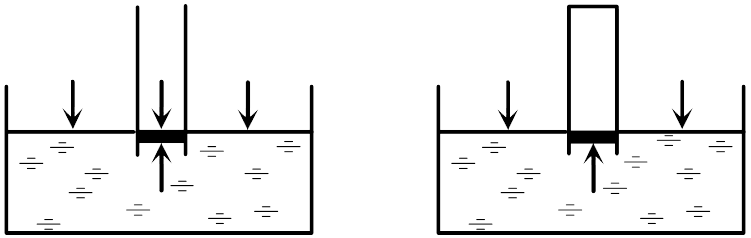 
Если бы трубка была открыта (см. левый рисунок), то жидкость не поднялась бы в трубке. Действительно, в этом случае на бесконечно малый элемент жидкости в трубке около поверхности (выделен на рисунке) действовали бы сила со стороны атмосферного воздуха в трубке, направленная вниз. С другой стороны, атмосферный воздух действует и на остальную поверхность жидкости, и это воздействие благодаря закону Паскаля передается выделенному элементу жидкости в трубке снизу. Таким образом, воздействие воздуха на поверхность жидкости в трубке и на свободную поверхность жидкости компенсируют друг друга, если уровень жидкости в трубке совпадает с уровнем жидкости в остальном сосуде. Если же мы поднимаем трубку, выпустив из нее воздух, на рассматриваемый элемент жидкости воздух сверху не действует (его нет в трубке), поэтому воздействие воздуха на свободную поверхность жидкости приведет к тому, что жидкость войдет в трубку и заполнит ее. При вытаскивании трубки жидкость будет подниматься вслед за ней. Однако при дальнейшем поднятии трубки наступит такой момент, когда воздействие воздуха на свободную поверхность и столба жидкости в трубке сравняются (в этот момент атмосферное давление будет равно гидростатическому давлению жидкости в трубке на уровне свободной поверхности). Дальнейший подъем трубки уже не приведет к поднятию жидкости — атмосферное давление не сможет «держать» столб жидкости большей высоты. Для воды этот столб составляет около 10 м, для ртути, с которой и экспериментировал Э. Торричелли, — 76 сантиметров. Таким образом, жидкость в трубке поднимается благодаря давлению атмосферного воздуха на поверхность воды в сосуде и закону Паскаля (ответ 4).
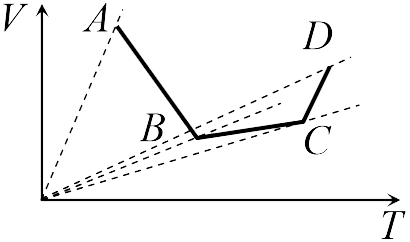
Сравнивая графики процессов 1, 2, 3 и 4, данные в условии задачи 13.1.6, с графиками изопроцессов, приведенными во введении к настоящей главе, заключаем, что: процесс 1 — изотермический, 2 — изохорический, 3 — изобарический. В процесс 4 меняются и давление, и объем, и температура газа (ответ 4).
Изохорическим охлаждением в задаче 13.1.8 является процесс 4 (см. рисунок)
В двух последних задачах этого варианта нужно с помощью закона Клапейрона-Менделеева вычислить один из параметров газа, если даны остальные параметры. В задаче 13.1.9 из закона Клапейрона-Менделеева
|
получим
|
(ответ 1).
В задаче 13.1.10 при вычислениях следует не забыть перевести температуру газа в Кельвины. Из закона Клапейрона-Менделеева находим
|
(ответ 1).
Из уравнения состояния в форме 
(13.2) следует, что при одинаковых объемах и температурах давление идеального газа определяется только полным числом молекул. Поэтому отношение давления водорода 
и гелия 
в задаче 13.2.1 равно 2 (ответ 2).
Поскольку перегородка в задаче 13.2.2 подвижная и находится в равновесии, давления газа в отсеках сосуда слева и справа от перегородки равны. Применяя к ним при этом условии закон Клапейрона-Менделеева, получим
для гелия | для азота |
где температуры 
и массы газов 
по условию одинаковы. Деля эти уравнения друг на друга, находим отношение объемов частей сосуда
|
(ответ 4).
Если бы точки, отвечающие состояниям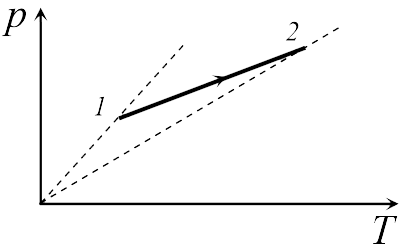 
1 и 2 в задаче 13.2.3, лежали на одной прямой, продолжение которой проходит через начало координат, то эти состояния принадлежали бы одной и той же изохоре, и, следовательно, объем газа в этих состояниях был одинаковым (см. формулу (13.6)). Поэтому для сравнения объемов этих состояний построим изохоры, проходящие через точки 1 и 2, и сравним отвечающие им объемы (см. рисунок; изохоры, проходящие через точки 1 и 2, показаны пунктиром).
Из формулы (13.6) следует, что чем больше объем, тем меньше коэффициент перед 
в зависимости (13.6), и, следовательно, меньше наклон соответствующей изохоры к оси температур. Поэтому изохоре 1 отвечает больший объем, чем изохоре 2, и, следовательно, объем газа в процессе 1-2 уменьшается 
(ответ 2).
Аналогичные рассуждения в задаче 13.2.4 показывают, что наибольшему давлению отвечает изобара, проходящая через точку 
(поскольку соответствующая прямая имеет наименьший наклон к оси температур; см. рисунок ниже). Поэтому правильный ответ в этой задаче — 3.
|
В закон Клапейрона-Менделеева входит абсолютная температура газа, поэтому данные в задаче 13.2.5 значения нужно перевести в Кельвины. В результате для отношения давлений газа в конечном 
и начальном 
состояниях получаем
|
(ответ 4).
Как следует из опыта, при приведении тел в тепловой контакт выравниваются их температуры. Это же касается и частей одного тела или даже компонент смеси газов (задача 13.2.6). Поэтому температуры компонент смеси будут одинаковы (ответ 1). Что касается парциальных давлений, плотностей или концентрации компонент смеси, то их значения зависят от количества молекул каждой компоненты смеси и могут быть различны.
Парциальное давление компонент смеси – это давление, которое оказывают только молекулы каждой компоненты. Как следует из формулы (13.8) парциальное давление любой компоненты можно найти, применяя только к ней закон Клапейрона-Менделеева и считая, что она имеет такую же температуру, как и вся смесь, и занимает такай же объем, как и вся смесь газов. Поэтому отношение парциальных давлений отдельных компонент смеси равно отношению количеств вещества (или числа молекул) этих компонент. Поэтому для отношения парциальных давлений углекислого газа 
и гелия 
в сосуде в задаче 13.2.7 имеем 
(ответ 2).
Как следует из закона Дальтона, давление смеси газов определяется полным количеством молекул в ней. Поэтому для анализа изменения давления смеси газов при протекании в ней химической реакции (задача 13.2.8) необходимо исследовать изменение числа молекул. Гелий не участвует в химической реакции — один моль гелия был и в начальном, и в конечном состоянии смеси. С озоном происходила реакция
|
т.е. из двух молекул озона в результате реакции получились три молекулы кислорода. Поэтому два моля озона превратились в три моля кислорода, и общее количество вещества смеси стало равно четырем молям. Поэтому давление смеси увеличивается в 4/3 раза (ответ 2).
Поскольку объемы и температуры газов одинаковы (задача 13.2.9), для сравнения их давлений необходимо сравнить число молекул в них. По условию в одном сосуде находится один моль азота, в другом 1 г водорода 
(т.е. половина моля) и 3 • 1023 молекул гелия 
(тоже половина моля). Поэтому и в одном и в другом сосуде находятся одинаковые количества молекул, и, следовательно, давление газов в них одинаково (ответ 3).
Плотность газа (задача 13.2.10) можно найти из следующей цепочки формул
|
(ответ 4). Здесь 
— масса газа, 
— масса одной молекулы газа.
Источник
1. Кем и когда проводился опыт, в чем состояла его цель
Первый газовый закон был открыт Робертом Бойлем и опубликован в 1660 г. в работе «Новые эксперименты, касающиеся воздушной пружины». Р. Бойль на основе тщательно поставленного количественного эксперимента доказал, что «упругости [давления] газа обратно пропорциональны объемам». В ходе исследований им была предпринята попытка количественно исследовать зависимость объема сжатого газа от температуры. Однако точных данных, подтверждающих эту зависимость, Р. Бойль не получил.
Исследования по расширению воздуха при нагревании проводил Г. Амонтон. Позднее аналогичные опыты ставили А. Вольта, Д. Дальтон, Дж. Пристли, Т. Соссюра и др.
Считается, что первые удовлетворительные измерения при исследовании теплового расширения газов получил в 1801 г. английский физик и химик Джон Дальтон (1766–1844 гг.). Он обнаружил, что кислород, водород и углекислый газ при нагревании вели себя одинаково.
 |
|
По полученным результатам Д. Дальтон в чрезвычайно осторожной форме формулирует вывод: «В общем, я не вижу достаточной причины, мешающей нам заключить, что все «упругие» газы при одном и том же давлении одинаково расширяются при нагревании».
Аналогичный вывод получил Ж. Л. Гей-Люссак в 1802 г. Но его утверждение было более определенным, чем высказывание Д. Дальтона. Видимо, поэтому закон о тепловом расширении газов называют не именем Д. Дальтона, а именем Ж. Л. Гей-Люссака.
Прибор, которым пользовался Гей-Люссак, показан на Рис. 2. Газ, тщательно осушенный, находится в баллончике. В трубке находится капля ртути, запирающая газ. Трубки расположены горизонтально, поэтому изменения давления при расширении не происходит.
 |
|
Пятнадцатью годами раньше Гей-Люссака (в 1787 г.) исследования этого вопроса были, без какой бы то ни было публикации, предприняты французским физиком Жаком Шарлем (1746–1823 гг.). Шарль нашел, что кислород, азот, углекислый газ и воздух расширяются одинаково в интервале температур между 0 и 100 ºС. Гей-Люссак знал о работах коллеги и настоял на том, чтобы второй газовый закон носил имя Жака Александра Сезара Шарля. Следует отметить, что в некоторых странах, в том числе и в России, этот закон известен все же как закон Гей-Люссака. В публикациях по истории науки приоритет открытия третьего газового закона – закона изменения давления газа в зависимости от температуры – обычно не обсуждается. Исследованием этой зависимости, как и зависимости объема газа от температуры, занимались многие ученые, изучавшие свойства газов в XVII–XVIII столетиях. История открытия закона теплового расширения газов связана с историей изобретения и усовершенствования термометров.
Первым прибором для измерения «жары» и «холода» в теле является воздушный термоскоп Г. Галилея (1597 г.). Суть опыта, который послужил толчком к созданию термоскопа, состояла в следующем. Небольшую колбу, размером с яйцо, с длинным и тонким, как пшеничный стебель, горлышком, опущенным в чашу с водой, согревают руками. Если убрать руки, то вода из чаши, по мере остывания воздуха в колбе, начнет подниматься в горлышко. Бенедетто Кастелли, ученик Г. Галилея, в 1638 г. пишет: «Этот эффект вышеупомянутый синьор Галилей использовал для изготовления инструмента для определения степени жары и холода».
Эванджелиста Торричелли преобразовал воздушный термоскоп Г. Галилея в жидкостный (спиртовый) термометр. Термометр Э. Торричелли – так называемый «флорентийский термометр» – был очень удобен в использовании и поэтому получил в XVII веке всеобщее признание. Термометры этого типа были введены в Англии Р. Бойлем, они быстро распространились и во Франции.
Усовершенствованием воздушного термометра Г. Галилея занимался Г. Амонтон – французский физик, член Парижской академии наук (1699 г.). В 1702 г. он сконструировал термометр, очень похожий по своей принципиальной схеме на современный газовый. Термометр Г. Амонтона представлял собой U-образную стеклянную трубку, более короткое колено которой заканчивалось резервуаром, содержащим воздух. В длинное колено наливалась ртуть в количестве, необходимом для поддержания постоянства объема воздуха в резервуаре. По высоте столба ртути определялась температура воздуха в резервуаре.
 |
|
Интересно отметить, что, работая с этим инструментом, именно Амонтон нашел прямо пропорциональную зависимость между температурой и давлением газа и пришел к понятию абсолютного нуля, который по его данным соответствовал температуре в –239,5 °С (1703 г.).
В 1954 X Генеральная конференция по мерам и весам установила термодинамическую температурную шкалу с одной реперной точкой — тройной точкой воды, температура которой принята 273,16 К (точно), что соответствует 0,01 °C, так что по шкале Цельсия абсолютному нулю соответствует температура −273,15 °C.
2. Приборы и материалы, необходимые для постановки опыта, принципиальная схема опытной установки
Установки для опытов по исследованию зависимости давления газа от температуры при постоянном объеме были достаточно сложными.
| |
|
Рассмотрим принципиальную схему экспериментальной установки для исследования зависимости давления газа от температуры при постоянном объеме. Основной частью такой установки является большая колба, в которой находился газ. Колба помещается в сосуд с водой. Об изменении давления газа можно судить по показаниям ртутного манометра, соединенного с колбой. Температура газа измеряется с помощью ртутного термометра.
 |
|
Ж. Шарль исследовал зависимость давления от температуры для следующих газов: кислород, азот, углекислый газ и воздух.
3. Порядок проведения опыта
Наполнив колбу тающим льдом, Шарль измерял давление, соответствующее температуре 0 ºС. Затем температура воды в большом сосуде менялась, что приводило к изменению высоты столба ртути в манометре. Подогревая воду в сосуде, окружающем колбу, Шарль отмечал температуру газа по термометру, а соответствующее давление – по манометру.
При проведении опыта влияние ряда факторов искажало ход эксперимента. Во-первых, вследствие нагревания, колба с газом частично меняла свой объем, соответственно строгое постоянство объема исследуемого газа не обеспечивалось. Во-вторых, газ, находящийся в так называемом «вредном пространстве» (в тонкой подводящей к манометру трубке), не нагревался так же, как в колбе. В-третьих, наличие в газе примесей (в частности, конденсирующихся паров) приводило к тому, что часть составляющих газ компонентов при повышении давления переходило в жидкое состояние. Действовали и другие факторы.
Попытки ученых исключить вредное воздействие побочных эффектов на ход эксперимента и приводили, как правило, к усложнению конструкции установки.
4. Основные результаты опыта
Опыты Ж. Шарля показали следующие результаты.
Приращение давления газа некоторой массы при нагревании на 1 ºС составило определенную часть αpтого давления, которое имел газ при температуре 0 ºС. Таким образом, приращение давления оказалось пропорциональным приращению температуры.
Величину αp называют температурным коэффициентом давления. Исследовав ряд газов, Шарль получил для них примерно одинаковое значение температурного коэффициента давления, а именно величину, равную примерно 1/273 ºС–1.
Таким образом, давление некоторой массы газа при нагревании на 1 ºС при неизменном объеме увеличивается на 1/273 часть давления, которое эта масса газа имела при 0 ºС.
5. Объяснение результатов опыта
В современной формулировке этот закон звучит следующим образом:
При неизменном объеме отношение давления данной массы газа к его абсолютной температуре есть величина постоянная.
Математически закон Ж. Шарля можно записать в виде:
Закон Шарля может быть записан в виде:
где P0 – давление газа при T = T0 = 273,15 К (то есть при температуре 0 °С). Коэффициент, равный 1/273,15 К–1, называют температурным коэффициентом давления.
На рисунке представлена зависимость давления данной массы газа от его температуры. Для различных температур газа расположение кривой зависимости на координатной плоскости различно. Изохоры, изображающие зависимость P от T для газа, который подчиняется закону Шарля, представляют собой прямые линии, располагающиеся на графике тем выше, чем меньше объем.
 |
|
Закон Шарля справедлив только для идеального газа. Он применим с определенной степенью точности к реальным газам при низких давлениях и невысоких температурах (например, атмосферный воздух, продукты сгорания в газовых двигателях и пр.)
Объяснение закону, установленному Шарлем, может быть дано с позиций молекулярно-кинетических представлений о строении вещества.
С точки зрения молекулярной теории возможны две причины увеличения давления данного газа: во-первых, может увеличиться число ударов молекул за единицу времени на единицу площади; во-вторых, возможно увеличение импульса, передаваемого при ударе стенки сосуда одной молекулой. И та, и другая причина требуют увеличения скорости молекул (при этом объем данной массы газа остается неизменным). Отсюда становится ясным, что повышение температуры газа как макрохарактеристики соответствует увеличению скорости беспорядочного движения молекул как характеристики микромира.
При очень высоких давлениях увеличивается взаимодействие между молекулами газа и наблюдаются отклонения от линейного закона Шарля.
Закон Шарля выводится как частный случай из уравнения Менделеева–Клапейрона:
где R – универсальная газовая постоянная (R = 8,31441 Дж/моль∙К), ν – число молей вещества, P – давление газа, V – объем газа, T – температура газа.
Он может быть получен как следствие основного уравнения молекулярно-кинетической теории идеального газа:
где k = 1,38 Дж/К – постоянная Больцмана.
Источник