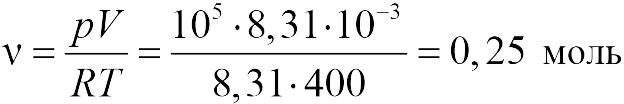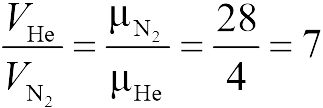Зависимость давления воздуха в сосуде от температуры

Задачи на газовые законы часто предлагаются школьникам на едином государственном экзамене. Для решения этих задач вполне достаточно знать уравнение состояния идеального газа (закон Клапейрона-Менделеева) и уметь использовать его алгебраически и геометрически (для построения графиков зависимости одних параметров газа от других) в простейших ситуациях. Кроме того, нужно понимать, как описываются смеси идеальных газов (закон Дальтона).
Уравнение, связывающее параметры газа друг с другом, называется уравнением состояния. Для идеального газа, взаимодействие молекул которого мало, уравнение состояния имеет вид
(13.1) |
где — давление газа, — концентрация молекул газа (число молекул в единице объема), — постоянная Больцмана, — абсолютная (в шкале Кельвина) температура. Учитывая, что , где — число молекул газа, — объем сосуда, в котором находится газ (часто говорят объем газа), получим из (13.1)
(13.2) |
Число молекул можно связать с количеством вещества газа : , где — число Авогадро. Поэтому формулу (13.2) можно переписать в виде
(13.2) |
где произведение постоянных Авогадро и Больцмана обозначено как . Постоянная = 8,31 Дж/(К•моль) называется универсальной газовой постоянной. Количество вещества газа можно также выразить через его массу и молярную массу этого газа
| (13.3) |
С учетом (13.3) закон (13.2) можно переписать и в таком виде
| (13.4) |
Уравнение состояния идеального газа (13.1)-(13.4), которое также называется уравнением (или законом) Клапейрона-Менделеева, позволяет связывать параметры идеального газа и проследить за их изменением в тех или иных процессах.
В школьном курсе физики рассматриваются три изопроцесса, в которых один из трех параметров газа (давление, температура и объем) не изменяется. В изобарическом процессе не изменяется давление газа, в изотермическом — температура, в изохорическом — объем. Изопроцессам отвечают следующие графики зависимости давления от объема, давления от температуры, объема от температуры.
Для изобарического процесса
|
Первые два графика очевидны. Последний получается так. Из закона Клапейрона-Менделеева следует, что зависимость объема от температуры при постоянном давлении имеет вид
| (13.5) |
где — постоянная. Графиком функции (13.5) является прямая, продолжение которой проходит через начало координат.
Для изохорического процесса
|
Второй график следует из соотношения
| (13.6) |
где — постоянная при постоянном объеме.
Для изотермического процесса
|
Первый график следует из закона Клапейрона-Менделеева, который при постоянной температуре газа можно привести к виду
| (13.7) |
где — постоянная. Отсюда следует, что графиком зависимости от в изотермическом процессе является гипербола.
Важнейшее свойство уравнения состояния идеального газа (13.1)-(13.4) заключается в том, что «индивидуальность» газа никак не проявляется в этих законах — единственный параметр собственно газа, входящий в уравнение состояния, — это число молекул. Например, 1 моль гелия и 1 моль азота, находящиеся в одинаковых объемах и имеющие одинаковые температуры, оказывают одинаковое давление. Отсюда следует, что и давление смеси идеальных газов определяется суммарным числом молекул всех компонент смеси:
| (13.8) |
где ![]() — число молекул первой, второй, третьей и т.д. компонент смеси, — постоянная Больцмана, — абсолютная температура смеси, — объем сосуда. Величины , имеющие смысл давления каждой компоненты смеси при условии, что она имела бы такую же температуру и занимала бы весь объем, называются парциальными давлениями компонент. Закон (13.8) называется законом Дальтона. Рассмотрим теперь в рамках этих законов предложенные выше задачи.
— число молекул первой, второй, третьей и т.д. компонент смеси, — постоянная Больцмана, — абсолютная температура смеси, — объем сосуда. Величины , имеющие смысл давления каждой компоненты смеси при условии, что она имела бы такую же температуру и занимала бы весь объем, называются парциальными давлениями компонент. Закон (13.8) называется законом Дальтона. Рассмотрим теперь в рамках этих законов предложенные выше задачи.
В задаче 13.1.1 из уравнения состояния в форме (13.1), получаем для давления в конце процесса :
т.е. давление газа увеличилось в 6 раз (ответ 1).
Применяя закон Клапейрона-Менделеева (13.2) к первому и второму газам (задача 13.1.2), получаем
где — искомый объем. Сравнивая первую и вторую формулы, заключаем, что (ответ 1).
Закон Клапейрона-Менделеева для газа в начальном и конечном состояниях (задача 13.1.3) дает
где — неизвестная температура. Из сравнения этих формул получаем , т.е. температуру газа в сосуде нужно повысить вдвое (ответ 2).
Из закона Клапейрона-Менделеева для начального и конечного состояний газа в задаче 13.1.4 имеем
Отсюда , т.е. количество вещества газа в сосуде увеличилось в 1,25 раза (ответ 3).
Первым, кто понял, почему жидкость поднимается вместе с трубкой (задача 13.1.5), и почему «природа боится пустоты» (Аристотель), но только до определенного предела, был знаменитый итальянский физик, современник Г. Галилея Э. Торричелли. Давайте рассмотрим рассуждения Торричелли подробно. Основная идея Торричелли заключалась в том, что атмосферный воздух оказывает давление на все поверхности, с которыми он контактирует. В равновесии жидкость занимает такое положение, чтобы все воздействия на каждый ее элемент компенсировались. 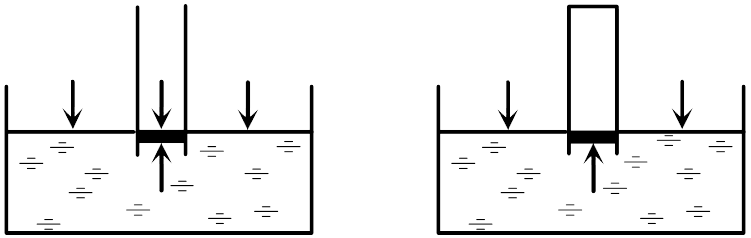 Если бы трубка была открыта (см. левый рисунок), то жидкость не поднялась бы в трубке. Действительно, в этом случае на бесконечно малый элемент жидкости в трубке около поверхности (выделен на рисунке) действовали бы сила со стороны атмосферного воздуха в трубке, направленная вниз. С другой стороны, атмосферный воздух действует и на остальную поверхность жидкости, и это воздействие благодаря закону Паскаля передается выделенному элементу жидкости в трубке снизу. Таким образом, воздействие воздуха на поверхность жидкости в трубке и на свободную поверхность жидкости компенсируют друг друга, если уровень жидкости в трубке совпадает с уровнем жидкости в остальном сосуде. Если же мы поднимаем трубку, выпустив из нее воздух, на рассматриваемый элемент жидкости воздух сверху не действует (его нет в трубке), поэтому воздействие воздуха на свободную поверхность жидкости приведет к тому, что жидкость войдет в трубку и заполнит ее. При вытаскивании трубки жидкость будет подниматься вслед за ней. Однако при дальнейшем поднятии трубки наступит такой момент, когда воздействие воздуха на свободную поверхность и столба жидкости в трубке сравняются (в этот момент атмосферное давление будет равно гидростатическому давлению жидкости в трубке на уровне свободной поверхности). Дальнейший подъем трубки уже не приведет к поднятию жидкости — атмосферное давление не сможет «держать» столб жидкости большей высоты. Для воды этот столб составляет около 10 м, для ртути, с которой и экспериментировал Э. Торричелли, — 76 сантиметров. Таким образом, жидкость в трубке поднимается благодаря давлению атмосферного воздуха на поверхность воды в сосуде и закону Паскаля (ответ 4).
Если бы трубка была открыта (см. левый рисунок), то жидкость не поднялась бы в трубке. Действительно, в этом случае на бесконечно малый элемент жидкости в трубке около поверхности (выделен на рисунке) действовали бы сила со стороны атмосферного воздуха в трубке, направленная вниз. С другой стороны, атмосферный воздух действует и на остальную поверхность жидкости, и это воздействие благодаря закону Паскаля передается выделенному элементу жидкости в трубке снизу. Таким образом, воздействие воздуха на поверхность жидкости в трубке и на свободную поверхность жидкости компенсируют друг друга, если уровень жидкости в трубке совпадает с уровнем жидкости в остальном сосуде. Если же мы поднимаем трубку, выпустив из нее воздух, на рассматриваемый элемент жидкости воздух сверху не действует (его нет в трубке), поэтому воздействие воздуха на свободную поверхность жидкости приведет к тому, что жидкость войдет в трубку и заполнит ее. При вытаскивании трубки жидкость будет подниматься вслед за ней. Однако при дальнейшем поднятии трубки наступит такой момент, когда воздействие воздуха на свободную поверхность и столба жидкости в трубке сравняются (в этот момент атмосферное давление будет равно гидростатическому давлению жидкости в трубке на уровне свободной поверхности). Дальнейший подъем трубки уже не приведет к поднятию жидкости — атмосферное давление не сможет «держать» столб жидкости большей высоты. Для воды этот столб составляет около 10 м, для ртути, с которой и экспериментировал Э. Торричелли, — 76 сантиметров. Таким образом, жидкость в трубке поднимается благодаря давлению атмосферного воздуха на поверхность воды в сосуде и закону Паскаля (ответ 4).
 Сравнивая графики процессов 1, 2, 3 и 4, данные в условии задачи 13.1.6, с графиками изопроцессов, приведенными во введении к настоящей главе, заключаем, что: процесс 1 — изотермический, 2 — изохорический, 3 — изобарический. В процесс 4 меняются и давление, и объем, и температура газа (ответ 4).
Сравнивая графики процессов 1, 2, 3 и 4, данные в условии задачи 13.1.6, с графиками изопроцессов, приведенными во введении к настоящей главе, заключаем, что: процесс 1 — изотермический, 2 — изохорический, 3 — изобарический. В процесс 4 меняются и давление, и объем, и температура газа (ответ 4).
 Изохорическим охлаждением в задаче 13.1.8 является процесс 4 (см. рисунок)
Изохорическим охлаждением в задаче 13.1.8 является процесс 4 (см. рисунок)
В двух последних задачах этого варианта нужно с помощью закона Клапейрона-Менделеева вычислить один из параметров газа, если даны остальные параметры. В задаче 13.1.9 из закона Клапейрона-Менделеева
|
получим
|
(ответ 1).
В задаче 13.1.10 при вычислениях следует не забыть перевести температуру газа в Кельвины. Из закона Клапейрона-Менделеева находим
|
(ответ 1).
Из уравнения состояния в форме (13.2) следует, что при одинаковых объемах и температурах давление идеального газа определяется только полным числом молекул. Поэтому отношение давления водорода и гелия в задаче 13.2.1 равно 2 (ответ 2).
Поскольку перегородка в задаче 13.2.2 подвижная и находится в равновесии, давления газа в отсеках сосуда слева и справа от перегородки равны. Применяя к ним при этом условии закон Клапейрона-Менделеева, получим
для гелия | для азота |
где температуры и массы газов по условию одинаковы. Деля эти уравнения друг на друга, находим отношение объемов частей сосуда
|
(ответ 4).
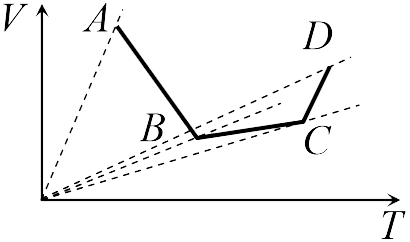
Если бы точки, отвечающие состояниям 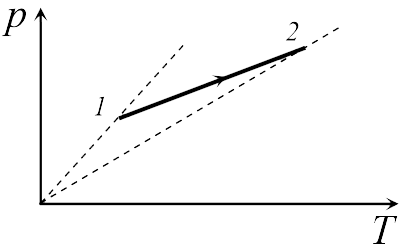 1 и 2 в задаче 13.2.3, лежали на одной прямой, продолжение которой проходит через начало координат, то эти состояния принадлежали бы одной и той же изохоре, и, следовательно, объем газа в этих состояниях был одинаковым (см. формулу (13.6)). Поэтому для сравнения объемов этих состояний построим изохоры, проходящие через точки 1 и 2, и сравним отвечающие им объемы (см. рисунок; изохоры, проходящие через точки 1 и 2, показаны пунктиром).
1 и 2 в задаче 13.2.3, лежали на одной прямой, продолжение которой проходит через начало координат, то эти состояния принадлежали бы одной и той же изохоре, и, следовательно, объем газа в этих состояниях был одинаковым (см. формулу (13.6)). Поэтому для сравнения объемов этих состояний построим изохоры, проходящие через точки 1 и 2, и сравним отвечающие им объемы (см. рисунок; изохоры, проходящие через точки 1 и 2, показаны пунктиром).
Из формулы (13.6) следует, что чем больше объем, тем меньше коэффициент перед в зависимости (13.6), и, следовательно, меньше наклон соответствующей изохоры к оси температур. Поэтому изохоре 1 отвечает больший объем, чем изохоре 2, и, следовательно, объем газа в процессе 1-2 уменьшается (ответ 2).
Аналогичные рассуждения в задаче 13.2.4 показывают, что наибольшему давлению отвечает изобара, проходящая через точку (поскольку соответствующая прямая имеет наименьший наклон к оси температур; см. рисунок ниже). Поэтому правильный ответ в этой задаче — 3.
|
В закон Клапейрона-Менделеева входит абсолютная температура газа, поэтому данные в задаче 13.2.5 значения нужно перевести в Кельвины. В результате для отношения давлений газа в конечном и начальном состояниях получаем
|
(ответ 4).
Как следует из опыта, при приведении тел в тепловой контакт выравниваются их температуры. Это же касается и частей одного тела или даже компонент смеси газов (задача 13.2.6). Поэтому температуры компонент смеси будут одинаковы (ответ 1). Что касается парциальных давлений, плотностей или концентрации компонент смеси, то их значения зависят от количества молекул каждой компоненты смеси и могут быть различны.
Парциальное давление компонент смеси – это давление, которое оказывают только молекулы каждой компоненты. Как следует из формулы (13.8) парциальное давление любой компоненты можно найти, применяя только к ней закон Клапейрона-Менделеева и считая, что она имеет такую же температуру, как и вся смесь, и занимает такай же объем, как и вся смесь газов. Поэтому отношение парциальных давлений отдельных компонент смеси равно отношению количеств вещества (или числа молекул) этих компонент. Поэтому для отношения парциальных давлений углекислого газа и гелия в сосуде в задаче 13.2.7 имеем (ответ 2).
Как следует из закона Дальтона, давление смеси газов определяется полным количеством молекул в ней. Поэтому для анализа изменения давления смеси газов при протекании в ней химической реакции (задача 13.2.8) необходимо исследовать изменение числа молекул. Гелий не участвует в химической реакции — один моль гелия был и в начальном, и в конечном состоянии смеси. С озоном происходила реакция
т.е. из двух молекул озона в результате реакции получились три молекулы кислорода. Поэтому два моля озона превратились в три моля кислорода, и общее количество вещества смеси стало равно четырем молям. Поэтому давление смеси увеличивается в 4/3 раза (ответ 2).
Поскольку объемы и температуры газов одинаковы (задача 13.2.9), для сравнения их давлений необходимо сравнить число молекул в них. По условию в одном сосуде находится один моль азота, в другом 1 г водорода (т.е. половина моля) и 3 • 1023 молекул гелия (тоже половина моля). Поэтому и в одном и в другом сосуде находятся одинаковые количества молекул, и, следовательно, давление газов в них одинаково (ответ 3).
Плотность газа (задача 13.2.10) можно найти из следующей цепочки формул
|
(ответ 4). Здесь — масса газа, — масса одной молекулы газа.
Источник
Страница 1 из 4
1
2
3
4
Вперёд >
Регистрация:
03.10.10
Сообщения:152
Благодарности:
71romk
Живу здесь
Регистрация:
03.10.10
Сообщения:
152
Благодарности:
71
Адрес:Тольятти
Формула изменения давления при изменении температуры
Есть закрытый бойлер косвенного нагрева объёмом 200 л. Температура воды 20. Давление 2 атм. Краны закрыты, расширительного бака нет. Какое давление будет при нагреве до 70 ?
Нужна формула или онлайн-калькулятор (в сети не нашел). Спасибо.
Регистрация:
12.05.12
Сообщения:7.491
Благодарности:
9.340Навигатор6989
Живу здесь
Регистрация:
12.05.12
Сообщения:
7.491
Благодарности:
9.340
Адрес:Минск
Вы же кран закрываете с одной стороны и в принципе давление не изменится
Регистрация:
25.06.12
Сообщения:2.333
Благодарности:
3.552Ovit1
Живу здесь
Регистрация:
25.06.12
Сообщения:
2.333
Благодарности:
3.552
Адрес:Екатеринбург
Посмотрите тематику “коэффициент объемного сжатия”/”модуль упругости”
Регистрация:
14.09.15
Сообщения:591
Благодарности:
332shadowmgn
Живу здесь
Регистрация:
14.09.15
Сообщения:
591
Благодарности:
332
Адрес:Магнитогорск
И не найдете. Давление увеличится на 53 МПа, т. е. бак разорвет еще при температуре 25-30 гр.
Регистрация:
03.10.10
Сообщения:152
Благодарности:
71romk
Живу здесь
Регистрация:
03.10.10
Сообщения:
152
Благодарности:
71
Адрес:Тольятти
@Навигатор6989 со стороны магистрали стоит обратный клапан и давление туда не сбрасывается.
Регистрация:
03.10.10
Сообщения:152
Благодарности:
71romk
Живу здесь
Регистрация:
03.10.10
Сообщения:
152
Благодарности:
71
Адрес:Тольятти
Почему нет формулы и таблиц? Вопрос ведь тривиальный в сантехнике. Гидробаки часто выходят из строя. 53 МПа от 10 градусов нагрева? Быть не может.
Регистрация:
14.09.15
Сообщения:591
Благодарности:
332shadowmgn
Живу здесь
Регистрация:
14.09.15
Сообщения:
591
Благодарности:
332
Адрес:Магнитогорск
Есть формулы, только нужно знать где смотреть. Тривиальная значит решайте. Не от 10 градусов, а при нагреве на 50 гр.
Регистрация:
12.10.16
Сообщения:149
Благодарности:
113hanke
Живу здесь
Регистрация:
12.10.16
Сообщения:
149
Благодарности:
113
Адрес:СПб
А зачем формула ? Вода при нагревании увеличивается в объеме до 4%, т. е. 200 л. + 8 л. Порвет все…Даже без формулы. Вода практически несжимаемая жидкость. Поставите клапан предохранительный, тот будет постоянно сливать эти 8 литров в канализацию. Просто добавьте расширительный бак для ГВС литров на 12-18.
Регистрация:
06.12.14
Сообщения:9
Благодарности:
1andoriu
Участник
Регистрация:
06.12.14
Сообщения:
9
Благодарности:
1Не надо бреда. У вас, что стенки бака из кальки? Никакого увеличения объема не будет, давление повысится и все. Баки из железа и расчитаны до 10 бар.
Топик-стартер,в вашем случае при начальном давлении 3 бара и 20 градусах будет 4,1 бара при 70. При 2 станет 3. Живите спокойно.Регистрация:
21.07.18
Сообщения:2.094
Благодарности:
1.011Honda_M
Живу здесь
Регистрация:
21.07.18
Сообщения:
2.094
Благодарности:
1.011
Адрес:Москва
Полная чушь. При таком увеличении давления не было бы никакой необходимости ставить расширительные баки на ГВС, а их ставить настоятельно рекомендуется.
Регистрация:
21.02.12
Сообщения:8.367
Благодарности:
11.227Юрген72
Живу здесь
Регистрация:
21.02.12
Сообщения:
8.367
Благодарности:
11.227
Адрес:Пермь
В моей практике было такое: новый водопровод из стальной трубы для опрессовки заполнили холодной водой из водопровода и подняли давление прессом до 12 бар, и так оставили, какое же было удивление когда через пару часов на манометре стало давление 17 бар А все из-за прогрева воды до почти комнатной температуры, т. е., градусов на 10-15. Вот для уменьшения этого эффекта и нужно ставить РБ.
Регистрация:
12.10.16
Сообщения:149
Благодарности:
113hanke
Живу здесь
Регистрация:
12.10.16
Сообщения:
149
Благодарности:
113
Адрес:СПб
Хм…
Вы физику в школе учили ? Даже полипропилен при нагревании удлиняется (увеличивается в объеме) и гнуться трубы. А вода обязательно. Причем вода увеличивается в объеме при нагревании https://sebestroj.ru/spravochnik/koehfficient-rasshirenija-vody.html. А так же при замерзании. Причем меньше чем при нагреве, но это не мешает воде рвать трубы).Регистрация:
12.10.16
Сообщения:149
Благодарности:
113hanke
Живу здесь
Регистрация:
12.10.16
Сообщения:
149
Благодарности:
113
Адрес:СПб
Я тут погорячился насчет НЕМНОГО при замерзании…Так как плотность воды равна 1000 кг на кубический метр, а плотность льда – 900, то оъбем увеличивается на (1000/900-1)*100%, что примерно равно 11%.
При нагреве всего до 4%Регистрация:
02.05.15
Сообщения:10.089
Благодарности:
4.920muai2
Живу здесь
Регистрация:
02.05.15
Сообщения:
10.089
Благодарности:
4.920@andoriu просто хотел воскресить некротему. Ляпнул че-то невнятное в пятницу, а сейчас понедельник и его вброс все еще опровергают…
Регистрация:
01.11.11
Сообщения:7
Благодарности:
0urru1
Участник
Регистрация:
01.11.11
Сообщения:
7
Благодарности:
0
Адрес:Салават
В инструкции по монтажу бойлера фирмы Будерус, на схеме обвязки, никакого расширительного бака не предусмотрено только предохранительный клапан.
Источник