Зависимость вязкости от диаметра сосуда

Движущей силойкровотока служит разность давлений между различными отделами сосудистого русла: кровь течет от области высокого давления к области низкого давления. Этот градиент давления служит источником силы, преодолевающей гидродинамическое сопротивление; последнее широко варьирует как во времени, так и в разных отделах сосудистого русла и зависит от архитектуры этого русла (например, числа, длины, диаметра и степени ветвления сосудов той или иной области) и вязкости крови [2, 4, 5, 15, 19, 20, 33].
Физические основы гемодинамики
Скорость кровотока, давление и сопротивление.
Все факторы, влияющие на кровоток, в конечном счете могут быть приближенно сведены к уравнению, сходному с законом Ома:
V’= DP/R(1)
Из этого уравнения следует, что объемная скорость кровотока V в каком-либо отделе кровеносного русла равна отношению разности среднего давления DР в артериальной и венозной частях этого отдела (или в любых других частях) к гидродинамическому сопротивлению R этого отдела.
Объемная скорость кровотока V’ отражает кровоснабжение того или иного органа. Она равна объему крови, протекающему через поперечное сечение сосудов, и измеряется в единицах мл/с. Ее можно вычислить, исходя из линейной скорости кровотока (v) через поперечное сечение сосуда и площади этого сечения (S =pr2):
V’=v·S. (2)
В соответствии сзаконом неразрывности струи объемная скорость тока жидкости в системе из трубок разного диаметра (т. е. в системе, подобной кровеносной) постоянна независимо от поперечного сечения трубки. Следовательно, для двух последовательных сегментов (а и б) (рис. 20.2) справедливо равенство
V’=va·Sa=vб·Sб (3)
Таким образом, если через последовательно соединенные трубки протекает жидкость с постоянной объемной скоростью, линейная скорость движения жидкости в каждой трубке обратно пропорциональна площади ее поперечного сечения.
Давление в кровеносной системе (артериальное и венозное) равно отношению силы, с которой кровь действует на стенки сосудов, к площади этих стенок. Поскольку в клинике кровяное давление издавна измеряется при помощи ртутных манометров, его
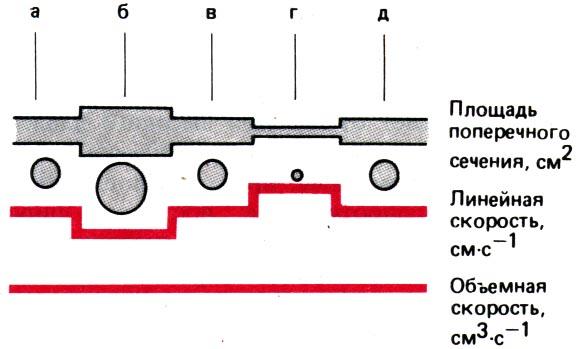
Рис. 20.2. Изменения линейной скорости кровотока и объемная скорость кровотока в последовательно соединенных трубках разного сечения
обычно выражают в миллиметрах ртутного столба, хотя иногда значения приводят в сантиметрах водного столба (1 мм рт. ст ≈ 13,6 мм вод. ст. ≈ 133 Па; 10 мм вод. ст. ≈ 98 Па).
Гидродинамическое сопротивление R нельзя измерить непосредственно, однако его можно вычислить из уравнения (1), зная разность давлений между двумя отделами сосудистой системы и объемную скорость.
Гидродинамическое сопротивление обусловлено внутренним трением между слоями жидкости и между жидкостью и стенками сосуда. Оно зависит от размеров сосуда, а также от вязкости и типа течения жидкости.
Гидродинамическое сопротивление в системе трубок.
Если трубки соединены последовательно, то их общее сопротивление в соответствии с первым законом Кирхгофа равно сумме сопротивления всех трубок:
R0=R1+R2+…(4)
Если же трубки соединены параллельно (как, например, сосудистые сети различных органов), то, согласно второму закону Кирхгофа, складываются их проводимости:
С0= C1 + С2+ … . (5)
Поскольку проводимость-это величина, обратная сопротивлению, то
C0=1/R1+ 1/R2+ … (6)
или в соответствии с уравнением (1)
V’ = DР • С, или С = V’/DP (7)
т.е. при постоянном градиенте давления объемная скорость возрастает пропорционально проводимости.
Учитывая, что проводимость есть величина, обратная сопротивлению, общее сопротивление системы из двух параллельных трубок равно
R0=1/(1/R1+ 1/R2) (8)
Таким образом, общее сопротивление нескольких параллельных трубок одинакового диаметра равно сопротивлению одной трубки, деленному на число трубок; таким образом, это общее сопротивление значительно меньше, чем у каждой отдельной трубки.
Вязкость крови. Если текущая жидкость соприкасается с неподвижной поверхностью (например, при движении жидкости в трубке), то слои такой жидкости перемещаются с различными скоростями. В результате между этими слоями возникает напряжение сдвига: более быстрый слой стремится вытянуться в продольном направлении, а более медленный задерживает его. Показателем, отражающим это «внутреннее сопротивление» жидкости, служит ее вязкость η.
Для многих жидкостей вязкость η – это постоянная величина, зависящая от температуры. Согласно уравнению Ньютона, эта величина равна отношению напряжения сдвига τ (силы, приходящейся на единицу площади) к градиенту скорости между соседними слоями g (скорости сдвига):
η= τ/g(Па·/с). (9)
Из уравнения Хагена-Пуазейля (см. ниже) следует, что на силы, сдвигающие слои жидкости относительно друг друга (т.е. приводящие жидкость в движение и поддерживающие это движение), влияет не только давление, но также радиус и длина сосуда. Вязкость часто выражают в относительных единицах, принимая вязкость воды при 20 °С (10-3Па·с) за 1,0.
Вязкость гомогенных (ньютоновских) жидкостей (например, воды, раствора электролитов, плазмы крови) постоянна. Кровь состоит из плазмы и форменных элементов и поэтому является гетерогенной (неньютоновской) жидкостью; вязкость ее варьирует в зависимости в основном от количества клеток и в меньшей степени от содержания белков в плазме. Кроме того, вязкость гетерогенных жидкостей зависит также от размеров (радиуса и длины) трубок, по которым они текут. У человека вязкость крови составляет 3-5, а плазмы-1,9-2,3относительных единиц (рис. 20.3).
Вязкость крови в сосудах. Приведенные выше значения относительной вязкости справедливы лишь для сравнительно быстрого тока крови (т.е. высокого напряжения сдвига) и нормального состава крови (гематокрит около 40 и содержание белков в плазме 6,5-8,0 г/дл). При низкой скорости кровотока (а следовательно, и при малом напряжении
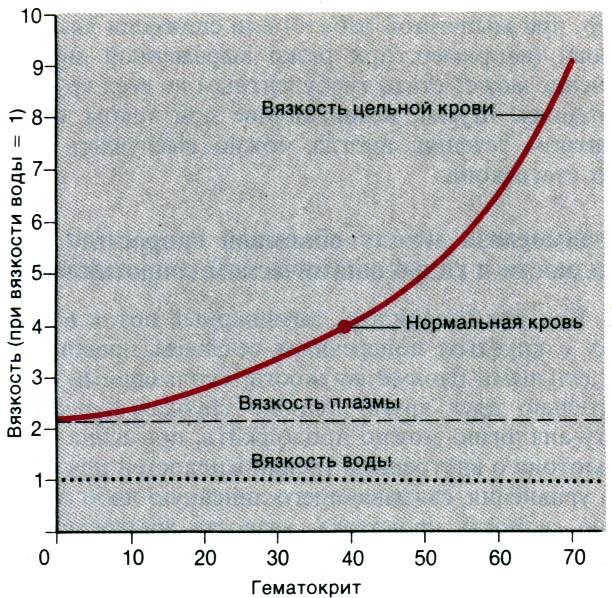
Рис. 20.3. Зависимость относительной вязкости крови от гематокрита
сдвига) вязкость увеличивается и при значительном снижении этих величин возрастает более чем до 1000 относительных единиц. В физиологических условиях эти эффекты проявляются лишь в наиболее мелких сосудах, где напряжение сдвига настолько мало, что эффективная вязкость может возрастать в 10 раз. Однако при некоторых патологических состояниях уменьшение скорости кровотока может сопровождаться еще большим повышением вязкости. Так, при сужении сосудов в участке, расположенном дистальнее места сужения, кровоток замедляется (подобное явление наблюдается в венулах, поперечное сечение которых больше, чем у капилляров). Увеличение вязкости крови в таких случаях приводит к еще большему падению скорости кровотока, и в конце концов он полностью прекращается. Повышение вязкости крови при замедлении кровотока объясняетсяобратимой агрегацией эритроцитов, образующих скопления в виде монетных столбиков или прилипающих к стенкам сосудов.
Агрегация эритроцитов обусловлена наличием в плазме крупных белков (фибриногена, α2-макроглобулина и т.д.). В патологических условиях тенденция к агрегации может настолько возрастать, что для продвижения крови требуется дополнительная энергия. Кроме того, при высоких скоростях кровотока эритроциты изменяют свою форму и соответствующим образом ориентируются по ходу струи; увеличение вязкости крови при низких скоростях кровотока частично обусловлено отсутствием этих эффектов [53].
Существует механизм, благодаря которому эффективная вязкость, наоборот, существенно снижается в сосудах диаметром менее 500 мкм. Это так называемыйфеномен сигма, или эффект Фареуса-Линдквиста. Этот феномен, более выраженный в мелких сосудах, обусловливает снижение эффективной вязкости крови в капиллярах вдвое по сравнению с крупными сосудами; таким образом, вязкость крови в капиллярах почти достигает значения вязкости плазмы. Это уменьшение вязкости, возможно, связано с ориентацией эритроцитов вдоль оси сосуда. При этом эритроциты выстраиваются в цепочку, которая передвигается по капилляру, подобно «змее», в оболочке из плазмы. Бесклеточная краевая зона с низкой вязкостью образует слой, относительно которого легко скользят клетки крови. В результате условия кровотока улучшаются, а перепады давления снижаются. Этот феномен противодействует, хотя бы частично, описанному выше эффекту увеличения вязкости крови при уменьшении скорости кровотока в мелких сосудах.
Типы течений жидкости
Ламинарное течение. В физиологических условиях почти во всех отделах кровеносной системы наблюдается ламинарное, или слоистое, течение крови. При таком типе течения жидкость движется как бы коаксиальными цилиндрическими слоями, причем все частицы ее перемещаются только параллельно оси сосуда. Остальные слои жидкости передвигаются относительно друг друга подобно трубкам телескопа, причем слой, непосредственно прилегающий к стенке сосуда, «прилипает» к ней и остается неподвижным; по этому слою скользит второй слой, по нему-третий и т.д. В результате образуетсяпараболический профиль распределения скоростей с максимумом в центре сосуда (рис. 20.4).
Чем меньше диаметр сосуда, тем ближе центральные «слои» жидкости к его неподвижной стенке и тем больше они тормозятся в результате вязкостного взаимодействия с этой стенкой. Вследствие этого в мелких сосудах средняя скорость кровотока ниже. В крупных же сосудах центральные слои расположены дальше от стенок, поэтому по мере приближения к длинной оси сосуда эти слои скользят относительно друг друга со все большей скоростью. В результате средняя скорость кровотока значительно возрастает.
Особенность ламинарного кровотока заключается в том, что чем крупнее частицы крови, тем ближе они располагаются к оси сосуда. В результатеосевой поток крови почти целиком состоит из эритроцитов, образующих довольно компактный цилиндр внутри оболочки из плазмы, содержащей мало клеток. Таким образом, средняя скорость кровотока выше, чем скорость тока плазмы.
Турбулентное течение. При определенных условиях ламинарное течение превращается в
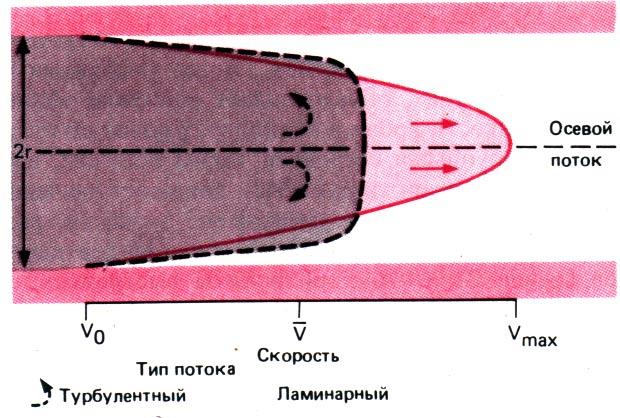
Рис. 20.4. Профили скоростей при ламинарном (коаксиальном, цилиндрическом) (сплошная красная кривая) и турбулентном (черная штриховая кривая) потоках. При турбулентном течении как скорость осевого потока, так и средняя скорость ниже, чем при ламинарном
турбулентное. Для турбулентного течения характерны завихрения, в которых частички жидкости перемещаются не только параллельно оси сосуда, но и перпендикулярно ей. Эти завихрения существенно увеличивают внутреннее трение жидкости, и профиль течения уплощается (рис. 20.4). При таком течении объемная скорость тока жидкости уже не пропорциональна градиенту давления (как при ламинарном кровотоке), так как по причине завихрений возникают дополнительные потери давления. Величина этих потерь пропорциональна квадрату объемной скорости тока жидкости, поэтому повышение последней сопровождается непропорциональным возрастанием давления.
Тип течения (турбулентный либо ламинарный) зависит от многих факторов. Существует безразмерная величина, отражающая все эти факторы в совокупности,-число Рейнольдса. Это число прямо пропорционально диаметру сосуда 2r (в метрах), средней линейной скорости кровотока v (в м/с) и плотности жидкости ρ (плотность крови составляет 1060 кг/м3) и обратно пропорционально вязкости жидкости η (в Па/с):
Re=2rvρ/η (10)
Если число Рейнольдса превышает 400, то у мест разветвлений и сужений артерий, а также в области крутых изгибов сосудов образуются локальные завихрения. Если же это число колеблется в пределах от 2000 до 2400, то поток становится целиком турбулентным. Во время периода изгнания в проксимальных отделах аорты и легочного ствола число Рейнольдса превышает это так называемоекритическое значение, поэтому поток в данных областях сосудистого русла временно становится турбулентным. При возрастании скорости кровотока (например,
при мышечной работе) или снижении вязкости крови (например, при резко выраженной анемии) течение может стать турбулентным во всех крупных артериях. Шумы, возникающие при таком турбулентном течении, иногда можно выслушать даже без стетоскопа.
Взаимосвязь между объемной скоростью тока жидкости и гидродинамическим сопротивлением
Как уже говорилось, ламинарный поток в трубках с круглым поперечным сечением представлен отдельными слоями жидкости, скользящими относительно друг друга подобно трубкам телескопа. Эту аналогию можно продолжить, применив закон Ньютона о внутреннем трении жидкостей для вывода уравнения, связывающего линейную либо объемную скорость кровотока, вязкость жидкости, градиент давления и размеры трубки (длину и внутренний радиус). В условиях стационарного состояния и ламинарного потока силы, создаваемые градиентом давления между двумя концами каждого концентрического слоя жидкости, должны быть уравновешены силами трения, создаваемыми между трущимися поверхностями этих слоев. При решении подобного уравнения можно получить параболический профиль скоростей, характерный для ламинарного потока; при этом средняя скорость тока жидкости будет зависеть от квадрата радиуса трубки.Объемная скорость кровотока будет рассчитываться исходя из закона Хагена-Пуазейля:
V =(π•r4/8ηl )• ΔP(11)
где ΔР – разность давлений, r- радиус сосуда, η-вязкость жидкости, l- длина сосуда. Коэффициент 8 появляется в результате интегрирования скоростей слоев.
Согласно закону Ома,гидродинамическое сопротивление потоку равно
R=8ηl/ π•r4 (12)
Поскольку V=vηr4 (уравнение (2)),средняя линейная скорость кровотока составляет
v=(r2/8ηl) )• ΔP (13)
Видно, что объемная скорость прямо пропорциональна, а гидродинамическое сопротивление обратно пропорционально радиусу трубки в четвертой степени. Поэтому обе эти величины гораздо больше зависят от изменений диаметра сосудов, чем от изменений их длины, градиента давления или вязкости жидкости. Так, если в исходном состоянии объемная скорость кровотока через сосуд равна
1 мл/с, то при увеличении его диаметра вдвое она составит 16 мл/с, а при увеличении вчетверо -256 мл/с; гидродинамическое же сопротивление при этом уменьшается соответственно в 16 и 256 раз.
С учетом этих соотношений ясно, что при местных или системных приспособительных реакциях сосудистого русла главную роль в регуляции давления и объемной скорости кровотока играют изменения радиуса сосудов.
Однако закон Хагена-Пуазейля имеет ограничения: так, он справедлив лишь для 1) жестких неветвящихся трубок с круглым поперечным сечением; 2) стационарного состояния и чисто ламинарного течения; 3) гомогенных жидкостей. В идеальном случае, когда все эти условия соблюдаются, сопротивление потоку минимально. Напротив, ситуация в сердечно-сосудистой системе совсем иная: сосуды эластичны и обладают сложной архитектурой с ветвлениями, кровоток не полностью непрерывен или турбулентен и кровь-это не гомогенная жидкость, Каждый из этих факторов в известной степени обусловливает увеличение гидродинамического сопротивления. Следовательно, кровоток в отдельных органах или сосудистой системе в целом не может быть точно описан уравнением Хагена-Пуазейля. Закон Ома также выполняется только при условии постоянного однонаправленного потока. Вследствие этого для более точного изучения гемодинамики необходимо разработать более тонкие методы, позволяющие учитывать дополнительные факторы, часть из которых оценить довольно сложно [5, 15, 33].
Соседние файлы в папке ССС
- #
- #
- #
- #
- #
- #
- #
Источник
Вязкость жидкости – это свойство реальных жидкостей оказывать сопротивление касательным усилиям (внутреннему трению) в потоке. Вязкость жидкости не может быть обнаружена при покое жидкости, так как она проявляется только при её движении. Для правильной оценки таких гидравлических сопротивлений, возникающих при движении жидкости, необходимо прежде всего установить законы внутреннего трения жидкости и составить ясное представление о механизме самого движения.
Физический смысл вязкости
Для понятия физической сущности такого понятия как вязкость жидкости рассмотрим пример. Пусть есть две параллельные пластинки А и В. В пространство между ними заключена жидкость: нижняя пластинка неподвижна, а верхняя пластинка движется с некоторой постоянной скоростью υ1
Как при этом показывает опыт, слои жидкости, непосредственно прилегающие к пластинкам (так называемые прилипшие слои), будут иметь одинаковые с ним скорости, т.е. слой, прилегающий к нижней пластинке А, будет находиться в покое, а слой, примыкающий к верхней пластинке В, будет двигаться со скоростью υ1.
Промежуточные слои жидкости будут скользить друг по другу, причем их скорости будут пропорциональны расстояниям от нижней пластинки.
Ещё Ньютоном было высказано предположение, которое вскоре подтвердилось опытом, что силы сопротивления, возникающие при таком скольжении слоев, пропорциональны площади соприкосновения слоев и скорости скольжения. Если взять площадь соприкосновения равной единице, это положение можно записать в виде
где τ – сила сопротивления, отнесенная к единице площади, или напряжение трения
μ – коэффициент пропорциональности, зависящий от рода жидкости и называемый коэффициентом абсолютной вязкости или просто абсолютной вязкостью жидкости.
Величину dυ/dy – изменение скорости в направлении, нормальном к направлению самой скорости, называют скоростью скольжения.
Таким образом вязкость жидкости – это физическое свойство жидкости, характеризующее их сопротивление скольжению или сдвигу
Вязкость кинематическая, динамическая и абсолютная
Теперь определимся с различными понятиям вязкости:
Динамическая вязкость. Единицей измерения этой вязкости является паскаль в секунду (Па*с). Физический смысл состоит в снижении давления в единицу времени. Динамическая вязкость характеризует сопротивление жидкости (или газа) смещению одного слоя относительно другого.
Динамическая вязкость зависит от температуры. Она уменьшается при повышении температуры и увеличивается при повышении давления.
Кинематическая вязкость. Единицей измерения является Стокс. Кинематическая вязкость получается как отношение динамической вязкости к плотности конкретного вещества.
Определение кинематической вязкости производится в классическом случае измерением времени вытекания определенного объема жидкости через калиброванное отверстие при воздействии силы тяжести
Абсолютная вязкость получается при умножении кинематической вязкости на плотность. В международной системе единиц абсолютная вязкость измеряется в Н*с/м2 – эту единицу называют Пуазейлем.
Коэффициент вязкости жидкости
В гидравлике часто используют величину, получаемую в результате деления абсолютной вязкости на плотность. Эту величину называют коэффициентом кинематической вязкости жидкости или просто кинематической вязкостью и обозначают буквой ν. Таким образом кинематическая вязкость жидкости
ν = μ / ρ,
где ρ – плотность жидкости.
Единицей измерения кинематической вязкости жидкости в международной и технической системах единиц служит величина м2/с.
В физической системе единиц кинематическая вязкость имеет единицу измерения см2/с и называется Стоксом(Ст).
Вязкость некоторых жидкостей
| Жидкость | t, °С | ν, Ст |
| Вода | 0,0178 | |
| Вода | 20 | 0,0101 |
| Вода | 100 | 0,0028 |
| Бензин | 18 | 0,0065 |
| Спирт винный | 18 | 0,0133 |
| Керосин | 18 | 0,0250 |
| Глицерин | 20 | 8,7 |
| Ртуть | 0,00125 |
Величину, обратную коэффициенту абсолютной вязкости жидкости, называют текучестью
ξ = 1/μ
Как показывают многочисленные эксперименты и наблюдения, вязкость жидкости уменьшается с увеличением температуры. Для различных жидкостей зависимость вязкости от температуры получается различной.
Поэтому, при практических расчетах к выбору значения коэффициента вязкости следует подходить очень осторожно. В каждом отдельном случае целесообразно брать за основу специальные лабораторные исследования.
Вязкость жидкостей, как установлено из опытов, зависит так же и от давления. Вязкость возрастает при увеличении давления. Исключение в этом случае является вода, для которой при температуре до 32 градусов Цельсия с увеличением давления вязкость уменьшается.
Что касается газов, то зависимость вязкости от давления, так же как и от температуры, очень существенна. С увеличением давления кинематическая вязкость газов уменьшается, а с увеличением температуры, наоборот, увеличивается.
Методы измерения вязкости. Метод Стокса.
Область, посвященная измерению вязкости жидкости, называется вискозиметрия, а прибор для измерения вязкости называется вискозиметр.
Современные вискозиметры изготавливаются из прочных материалов, а при их производстве используются самые современные технологии, для обеспечение работы с высокой температурой и давлением без вреда для оборудования.
Существует следующие методы определения вязкости жидкости.
Капиллярный метод.
Сущность этого метода заключается в использовании сообщающихся сосудов. Два сосуда соединяются стеклянной трубкой известного диаметра и длины. Жидкость помещается в стеклянный канал и за определенный промежуток времени перетекает из одного сосуда в другой. Далее зная давление в первом сосуде и воспользовавшись для расчетов формулой Пуазейля определяется коэффициент вязкости.
Метод по Гессе.
Этот метод несколько сложнее предыдущего. Для его выполнения необходимо иметь две идентичные капиллярные установки. В первую помещают среду с заранее известным значением внутреннего трения, а во вторую – исследуемую жидкость. Затем замеряют время по первому методу на каждой из установок и составляя пропорцию между опытами находят интересующую вязкость.
Ротационный метод.
Для выполнения этого метода необходимо иметь конструкцию из двух цилиндров, причем один из них должен быть расположен внутри другого. В промежуток между сосудами помещают исследуемую жидкость, а затем придают скорость внутреннему цилиндру.
Жидкость вращается вместе с цилиндром со своей угловой скоростью. Разница в силе момента цилиндра и жидкости позволяет определить вязкость последней.
Метод Стокса
Для выполнения этого опыта потребуется вискозиметр Гепплера, который представляет из себя цилиндр, заполненный жидкостью.
Вначале делаются две пометки по высоте цилиндра и замеряют расстояние между ними. Затем шарик определенного радиуса помещается в жидкость. Шарик начинает погружаться в жидкость и проходит расстояние от одной метки до другой. Это время фиксируется. Определив скорость движения шарика затем вычисляют вязкость жидкости.
Видео по теме вязкости
Определение вязкости играет большую роль в промышленности, поскольку определяет конструкцию оборудования для различных сред. Например, оборудование для добычи, переработки и транспортировки нефти.
Вместе со статьей “Вязкость жидкости” читают:
Источник
