Жидкость на стенках сосуда

4.2. Элементы гидростатики

4.2.3. Гидростатическое давление

Жидкость, находящаяся в некотором сосуде, оказывает на его дно и стенки гидростатическое давление.

Гидростатическое давление (давление жидкости) на дно сосуда (рис. 4.10) рассчитывают по формуле

pгидр = ρ0gh,

где ρ0 – плотность жидкости; g – модуль ускорения свободного падения; h – высота столба жидкости.

В Международной системе единиц гидростатическое давление измеряется в паскалях (1 Па).

Сила гидростатического давления на дно сосуда (см. рис. 4.10) определяется как произведение:

Fгидр = pгидрS = ρ0ghS,

где pгидр – гидростатическое давление на дно сосуда; ρ0 – плотность жидкости; g – модуль ускорения свободного падения; h – высота столба жидкости; S – площадь дна сосуда.

Рис. 4.10

Гидростатическое давление (давление жидкости) на вертикальную стенку сосуда (рис. 4.11) рассчитывают по формуле

p гидр = ρ 0 g h 2 ,

где ρ0 – плотность жидкости; g – модуль ускорения свободного падения; h – высота вертикальной стенки сосуда (столба жидкости).

Рис. 4.11

Сила гидростатического давления на вертикальную стенку сосуда (см. рис. 4.11) определяется как произведение:

F гидр = p гидр S = ρ 0 g h 2 S ,

где pгидр – гидростатическое давление на дно сосуда; ρж – плотность жидкости; g – модуль ускорения свободного падения; h – высота столба жидкости; S – площадь вертикальной стенки.

Рис. 4.11

При расчете давленияна днооткрытого водоема (рис. 4.12) необходимо учитывать атмосферное давление:

p = pатм + ρ0gh,

где pатм – атмосферное давление; ρ0 – плотность жидкости; g – модуль ускорения свободного падения; h – глубина водоема.

Рис. 4.12

Сила давления на дно открытого водоема определяется произведением:

F = pS = (pатм + ρ0gh)S,

где S – площадь дна водоема.

Гидростатическое давление жидкости на дно мензурки (рис. 4.13), отклоненной от вертикали на некоторый угол:

p = ρ0gh1 cos α,

где ρ0 – плотность жидкости; g – модуль ускорения свободного падения; h1 – высота столба жидкости при вертикальном положении мензурки; h2 = h1 cos α – высота столба жидкости при отклонении мензурки на угол α от ее вертикального положения.

Рис. 4.13

Пример 25. Цилиндрический сосуд радиусом 10 см имеет высоту 30 см. Его заполнили до краев жидкостью плотностью 2,5 г/см3. Найти величину средней силы гидростатического давления, действующей на боковую поверхность цилиндра.

Решение. Средняя сила гидростатического давления, действующая на боковую поверхность цилиндра, определяется произведением:

⟨ F гидр ⟩ = ⟨ p ⟩ S ,

где ⟨ p ⟩ – среднее гидростатическое давление на боковую поверхность цилиндра; S – площадь боковой поверхности цилиндра.

Найдем каждый из сомножителей следующим образом:

• среднее гидростатическое давление на боковую поверхность цилиндра

⟨ p ⟩ = ρ 0 g h 2 ,

где ρ0 – плотность жидкости, заполняющей сосуд; g – модуль ускорения свободного падения; h – высота цилиндра; т.е. среднее значение гидростатического давления определяется как давление на середину боковой поверхности цилиндра;

• площадь боковой поверхности цилиндра

S = 2πRh,

где 2πr – длина окружности; R – радиус дна цилиндра; т.е. площадь боковой поверхности цилиндра определяется как площадь прямо­угольника, одна из сторон которого равна высоте цилиндра, а другая – периметру круга (длине окружности), лежащего в его основании.

Подстановка среднего гидростатического давления ⟨ p ⟩ и площади боковой поверхности цилиндра S в исходную формулу позволяет получить выражение для вычисления модуля искомой силы:

⟨ F гидр ⟩ = π ρ 0 g R h 2 .

Расчет дает значение:

⟨ F гидр ⟩ = π ⋅ 2,5 ⋅ 10 3 ⋅ 10 ⋅ 10 ⋅ 10 − 2 ⋅ ( 30 ⋅ 10 − 2 ) 2 ≈ 707 Н ≈ 0,71 кН.

Пример 26. Атмосферное давление составляет 100 кПа. Плотность воды в водоеме равна 1,0 г/см3. Найти глубину открытого водоема, на которой давление в четыре раза больше атмосферного.

Решение. Давление в открытом водоеме определяется формулой

p = pатм + ρ0gh,

где pатм – атмосферное давление; ρ0 – плотность воды; g – модуль ускорения свободного падения; h – искомая глубина водоема.

По условию задачи

p = 4pатм.

Подстановка указанного значения в исходную формулу дает:

4pатм = pатм + ρ0gh,

или

3pатм = ρ0gh.

Выразим отсюда искомую глубину водоема

h = 3 p атм ρ 0 g

и произведем вычисление:

h = 3 ⋅ 100 ⋅ 10 3 1,0 ⋅ 10 3 ⋅ 10 = 30 м.

Таким образом, давление в открытом водоеме в 4 раза превышает атмосферное на глубине 30 м.

Источник

Содержание:

• § 1 Особенности давления в жидкости и газе
• § 2 Формула для вычисления давления в жидкостях и газах
• § 3 Решение задачи по теме урока
• § 4 Краткие итоги по теме урока

§ 1 Особенности давления в жидкости и газе

Известно, что давление, производимое на жидкости и газы, передается в каждую точку без изменения по всем направлениям. Это утверждение называется законом Паскаля.

На жидкости, как и на все тела на Земле, действует сила тяжести. Поэтому верхние слои жидкости давят на нижележащие слои, это давление по закону Паскаля передается по всем направлениям. Значит, внутри жидкости существует давление. Чтобы убедиться в этом, поставим опыт.

Возьмем стеклянную трубочку, затянутую снизу резиновой пленкой. Если в трубочку нальем воду, то увидим, что резиновая пленка прогибается. На резиновую пленку действуют две силы: вес воды, направленный вниз, из-за чего пленка изменяет свою форму, и возникающая при деформации сила упругости, которая стремится восстановить первоначальную форму и направленная вверх. Если две эти силы равны, то пленка будет находиться в покое.

Опустим трубку с водой в другой, более широкий, сосуд с водой. Возникает третья сила, действующая на резиновую пленку, – сила давления воды снизу, она направлена вверх и заставляет пленку выпрямляться. Если уровни воды в трубке и в сосуде совпадут, то силы давления, действующие сверху и снизу на пленку, окажутся равными.

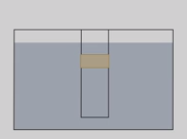
Такой же опыт проведем с трубкой, в которой есть боковое отверстие, затянутое резиновой пленкой. Если в трубку налить воду, то пленка выгибается наружу, так как вода давит не только на дно трубки, но и на стенки. Опустим трубку в воду и заметим, что пленка выпрямляется, то есть силы, действующие на пленку изнутри и снаружи, оказались равными.

Итак, опыты показывают, что внутри жидкости существует давление и на одном и том же уровне оно одинаково по всем направлениям.

Такое же утверждение справедливо и для газов.

§ 2 Формула для вычисления давления в жидкостях и газах

От чего зависит давление в жидкостях и газах?

Вспомним определение давления.

Давление – скалярная физическая величина, равная отношению силы, действующей перпендикулярно поверхности, к площади этой поверхности: p = F/S.

Сила давления Fравна весу P: P = mg.

Мы знаем, что массу тела можно найти по плотности вещества: m = ρV, где ρ – плотность, V – объем.

Объем жидкости, находящейся в сосуде в форме прямоугольного параллелепипеда или в форме цилиндра, можно найти, умножив площадь дна на высоту сосуда: V = Sh. Подставим формулы веса, массы, объема в формулу давления и, сократив площадь, получим:

Мы вывели формулу для вычисления давления в жидкостях и газах:

p = gρh.

Из этой формулы видно, что давление жидкости на дно сосуда зависит только от плотности и высоты столба жидкости.

По формуле p = gρhможно рассчитывать:

1)давление жидкости на дно в сосуде любой формы, то есть давление жидкости не зависит от формы сосуда;

2)давление жидкости на стенки сосуда, так как давление на одной и той же глубине одинаково по всем направлениям: вверх, вниз, вправо, влево, вперед, назад;

3)давление в газах.

Проверим единицу измерения давления по формуле p = gρh.

g – коэффициент тяжести, измеряется в Н/кг,

ρ – плотность, в международной системе единиц измеряется в кг/м3,

h – высота столба жидкости (глубина) – в м.

§ 3 Решение задачи по теме урока

Рассмотрим решение задачи:

Задача:Определить давление воды на дно морской впадины, глубина которой 10900 м. Плотность морской воды – 1030 кг/м3.

Решение: Запишем условие задачи: нам известны глубина h = 10900 м, плотность ρ = 1030 кг/м3. Необходимо найти: давление p. Для решения: запишем формулу расчета давления в жидкостях и газах p = gρh и подставим числовые значения:

p = 10 Н/кг · 1030 кг/м3· 10 900 м = 112 270 000 Па = 112, 27 МПа.

Ответ: 112, 27 МПа

§ 4 Краткие итоги по теме урока

ВАЖНО ЗАПОМНИТЬ:

На жидкости и газы действует сила тяжести, поэтому они обладают весом. Вышележащие слои жидкости и газа своим весом давят на нижележащие слои, то есть оказывают давление. Давление внутри жидкости и газа на одном и том же уровнеодинаково по всем направлениям.

Давление в жидкостях и газах рассчитывается по формуле p = gρh, где g – коэффициент тяжести, ρ – плотность, h – высота столба жидкости или газа.

Давление в жидкостях и газах зависит только от плотности и высоты столба жидкости или газа и не зависит от формы и площади поперечного сечения сосуда, в котором находится жидкость или газ.

Список использованной литературы:

1. Волков В.А. Поурочные разработки по физике: 7 класс. – 3-е изд. – М.: ВАКО, 2009. – 368 с.
2. Волков В.А. Тесты по физике: 7-9 классы. – М.: ВАКО, 2009. – 224 с. – (Мастерская учителя физики).
3. Кирик Л.А. Физика -7. Разноуровневые самостоятельные и контрольные работы. М.: Илекса, 2008. – 192 с.
4. Контрольно-измерительные материалы. Физика: 7 класс / Сост. Зорин Н.И. – М.: ВАКО, 2012. – 80 с.
5. Марон А.Е., Марон Е.А. Физика. 7 Дидактические материалы. – М.: Дрофа, 2010. – 128 с.
6. Перышкин А.В. Физика. 7 класс – М.: Дрофа, 2011.
7. Тихомирова С.А. Физика в пословицах и поговорках, стихах и прозе, сказках и анекдотах. Пособие для учителя. – М.: Новая школа, 2002. – 144 с.
8. Я иду на урок физики: 7 класс. Часть III: Книга для учителя. – М.: Издательство «Первое сентября”, 2002. – 272 с.

Источник

Давление жидкости на сосуд при е6 движении 183, 186  [c.358]

Опираясь на этот же принцип, Бенедетти отвергает аристотелевскую теорию падения тел, выдвигая прямо противоположную ей. Свое доказательство он строит на простом мысленном эксперименте делит падающее тело на несколько равных по объему и весу частей и утверждает, что скорости падения их всех будут одинаковы, поскольку нет причин, которые помешали бы этому. Убыстрение же движения тел при падении он объясняет возрастанием все той же стремительности при непрерывном действии постоянной силы, а не увеличением веса, как учили схоласты. Это было первое открытое, ясное и доказательное выступление с утверждением независимости времени и скорости падения от веса тел. Принцип инерции движения позволяет Бенедетти высказать предположение о существовании центробежной силы (инерции) если тело, движущееся по кругу, не прикреплено, оно будет удаляться под действием этой силы по касательной к кругу подобно грязи, отскакивающей от колес экипажа . И наконец, изучая равновесие жидкости в сообщающихся сосудах, Бенедетти почти на 70 лет раньше Паскаля и за год до Стенина обнаруживает гидравлический парадокс – одинаковое давление жидкости на основание при равных высотах независимо от формы сосуда.  [c.56]

Решение упрощается при определении составляющей силы давления, действующей на стенку вдоль оси вращения сосуда, поскольку инерционные силы не проектируются на это направление. Осевая сила давления жидкости на стенку (рис. IV-7)  [c.80]

Указание. При вращении системы суммарная сила давления жидкости на поршень равна весу поршня. Это условие позволяет найти давление в центре поршня к, следовательно, во всех точках сосуда.  [c.94]

Если ро == Ра, внешнее давление при расчетах обычно не учитывают, так как оно с одинаковой силой воспринимается обеими сторонами стенки, и расчет ведут по избыточному давлению, т. е. давлению самой жидкости. На рис. 2.7, б приведены в качестве примера эпюры избыточного давления жидкости на боковые стенки и дно сосуда.  [c.22]

Сила давления жидкости на дно сосуда и его стенки. Предположим, что мы имеем три сосуда Л, В и С с плоскими днищами (рис. 47). При этом форма сосудов различна, но площадь дна со и глубина воды Н во всех сосудах одинаковы.  [c.67]

В данном учебном пособии рассмотрены задачи, посвященные определенным разделам гидравлики давлению жидкости на поверхности различного рода истечению жидкости из малых и больших отверстий сосудов разной формы при постоянном и переменном напорах определению работы, затрачиваемой при выкачивании жидкости, расширении и сжатии газа в цилиндре некоторые специальные вопросы гидравлики открытых русел и сооружений.  [c.3]

Решение. При значительных давлениях жидкости на стенки сосуда горизонтальная и вертикальная составляющие силы давления практически равны (Докажите это самостоятельно), поэтому будем  [c.49]

Вычисляем по формуле (2-2) сила давления жидкости на горизонтальное дно сосуда зависит при  [c.39]

Измерение уровня гидростатическим методом основано на измерении давления жидкости на дно резервуара, которое измеряется в открытых сосудах обычным или дифференциальным манометрами. В резервуарах, находящихся под давлением, уровень жидкости можно измерить только посредством дифференциального манометра. При использовании дифференциальных манометров место установки измерительного прибора не влияет на правильность индикации, если оно находится ниже уровня днища резервуара, а измерение давления осуществляется относительно давления постоянного уровня жидкости.  [c.102]

Давление может измеряться при помощи столба жидкости – ртути, воды, спирта и др., уравновешивающего давление газа. На рис. 1-1 изображен сосуд с газом. К стенке сосуда припаяна изогнутая трубка, наполненная какой-либо жидкостью. Давление в сосуде р1, а атмосферное давление рд, при этом pi > Под действием разности давлений pi-р жидкость в правом колене поднимется и уравновесит избыток давления в сосуде. Отсюда можно написать равенство  [c.13]

Если начало координат поместить на свободную поверхность покоящейся жидкости, на которой постоянное давление ро задано или для открытого сосуда равно атмосферному давлению, то, как следует из выражения (1.8), при z = О С = Ро- Подставив значение постоянной С в уравнение (1.8) и имея в виду, что pg = у, окончательно получим величину гидростатического давления в виде  [c.22]

Т. е. в сообщающихся сосудах при одинаковом давлении на свободных поверхностях высоты жидкостей, отсчитываемые от поверхности раздела, обратно пропорциональны плотностям жидкостей.  [c.32]

Жидкость подвержена действию двух категорий внешних сил объемных (массовых) и поверхностных. Объемными называются силы, пропорциональные объему жидкости (силы тяжести и силы инерции), поверхностными – силы, приложенные к поверхности, ограничивающей объем жидкости, или к поверхности, проведенной внутри этого объема. В общем случае (при равномерном распределении этих сил по поверхности) величина поверхностной силы пропорциональна площади, на которую она действует. В качестве примера поверхностной силы можно привести атмосферное давление, действующее на поверхность жидкости, помещенной в открытом сосуде.  [c.15]

На рис. 2.8 показан резервуар А, наполненный жидкостью, на поверхность которой действует давление Ро меньше атмосферного (например, из резервуара откачана часть воздуха при помощи вакуум-насоса). Точка К погружена в жидкость вспомогательного сосуда В на глубину h и соединена с резервуаром А изогнутой U-образной трубкой V, при помощи которой можно измерить давление в резервуаре А (такая трубка  [c.31]

На рис. 33 показан замкнутый сверху сосуд, вращающийся вокруг вертикальной оси и имеющий отверстие в центре крышки. Построим оси координат х, у, z с началом в точке О, расположенной в центре отверстия. Полагаем, что сосуд полностью заполнен жидкостью. В точке О, где х = у = z = О, давление рав но атмосферному р = рат- Это пограничное условие определяет постоянную интегрирования (63) равенством С = рат. Следовательно, здесь справедлив установленный выше закон распределения давления, выражающийся уравнением (64). При этом давление по плоскости Ох также будет определяться высотой столба жидкости, определяемой по зависимости (68).  [c.54]

Следовательно, реактивная сила, возникающая при вытекании жидкости из сосуда, направлена в сторону, противоположную движению струи. При этом реактивная сила в два раза больше силы гидростатического давления, которая действовала бы на плоскую задвижку в случае закрытия отверстия. В этом отношении мы имеем полную аналогию с активным давлением.  [c.223]

С тем, чтобы пояснить вопрос о неполном ударе, обратимся к рис. 9-22. При постепенном закрытии крана К, когда положительная волна давления (см. график I на рис. 9-22) отражается от жидкости в сосуде, мы получаем отрицательную отраженную волну, изображенную графиком II (рис. 9-22).  [c.364]

Задача 3.11. Сосуд Мариотта представляет собой плотно закрытый сосуд, в крышке которого укреплена трубка, сообщающая сосуд с атмосферой. Трубка может быть укреплена на различной высоте. В стенке сосуда имеется отверстие диаметром =10 мм, через которое происходит истечение в атмосферу. Какое давление установится в сосуде на уровне нижнего обреза трубки при истечении Определить скорость истечения и время опорожнения сосуда Мариотта от верха до нижнего обреза трубки. Объемом жидкости в трубке и сопротивлением при истечении пренебречь (е=1).  [c.52]

Предположим, что свободная поверхность жидкости в сосуде очень велика по отношению к отверстию. Все жидкие нити имеют свое начало на этой поверхности, где скорость V так мала, что ее можно считать равной нулю. Предположим, кроме того, что свободная поверхность находится под атмосферным давлением р . Тогда V я г обращаются в нуль одновременно при р=р , и это условие определяет постоянную С в предыдущем уравнении, которое принимает теперь вид  [c.301]

Гидростатика. Равновесие жидкости возможно только при силах, имеющих однозначный потенциал. Свободная поверхность жидкости есть эквипотенциальная поверхность. Тяжелая жидкость. Тяжелая вращающаяся жидкость. Вращающаяся жидкость, частицы которой притягиваются одной точкой и.т между собой по закону Ньютона. Сжатие Земли. Давления, которые жидкость производит на сосуд, в котором она заключается, или на погруженное твердое тело. Принцип  [c.110]

Последующие научные работы по гидравлике появились лишь в XVI и XVII веках. Наиболее крупные из них Леонардо да Винчи (1452-1519) – в области плавания тел, движения жидкости по трубам и открытым руслам С. Стевина (1548-1620) – законы давления жидкости на дно и стенки сосуда Г. Галилея (1564-1642) – в области равновесия и движения тел в жидкости Э. Торичелли (1608-1647)-по истечению жидкости через отверстия Б. Паскаля (1623-1662) – о передаче давления жидкости (закон Паскаля) И. Ньютона (1642-1727)-о внутреннем трении в жидкости (закон Ньютона) и сопротивлении тел при движении в жидкости.  [c.4]

Паскаль, как и многие до него, тоже часто пользуется понятием работа . При этом он распространяет его, а вместе с ним и принцип возможных перемещений, на жидкости. Во всех простых машинах – рычаге, блоке, бесконечном винте – путь увеличивается в той же пропорции, как и сила , в гидростатике же совершенно безразлично, заставить ли 100 фунтов воды пройти путь в один дюйм или один фунт воды – путь в 100 дюймов ,- писал Паскаль. Пользуясь этим принципом, он независимо и более четко и широко, чем Бенедетти, Стевин и Галилей, формулирует закон равного давления жидкостей на стенки сосудов, закон сообщающихся сосудов, принцип гидравлического пресса и другие положения гидростатики.  [c.76]

В учебном пособии рассмотрены математические приеш решения задач некоторых разделов гидравлики /технической гидромеханики/ давление жидкости на поверхности истечение жидкости из малых и больших отверстий сосудов различной ( ормы при постоянном и переменном напорах определение работы, эапрачиваемой при выкачивании жидкости, расширении и сжатии газа в цилиндре специальные вопросы гидравлики открытых русел и сооружений.  [c.2]

Сила давления жидкости на погруженное в нее тело при относительном покое в равномерно вращающемся сосуде складывается из подъемной архимедовой силы Рг = и дополнительной центростремительной силы  [c.619]

Интересно проследить, кок реактивная сила передается па стенки сосуда. Реактивная сила создается вследствие разности давлений на степки сосуда, разности, возникающей при вытекании струи. Давление на эадней стенке рис. 300) можно считать равным плюс гидростатическое давление ук (у – удельный вес жидкости, а Л – глубина точки), ибо скорость течения у этой степки очень мала, ничтожно мала по сравнению со скоростью в струе вытекающей жидкости. Давление на передней стенке сосуда (см. рис. 300), на гой стенке, в которой находится отверстие, не будет равным давлению на задней стенке. Если бы это было не так и давления на передней и задней стенках были бы одинаковы, то они уравновешивались бы во всех противолежащих площадках, за исключением площадки 5 = 5о, расположенной на задней стенке против отверстия площадью 5о. Поэтому общая сила давления жидкости на заднюю стенку, как и следовало ожидать, будет больше. Определим величину силы давления на площадку 5, полагая размеры ее очень малыми по сравиению с к. а сила Р, очевидно, будет равна  [c.374]

Термометр – прибор для измерения сравни-10льно низких температур (до 500°). Термометры изготовляются жидкостные, манометрические и сопротивления. Принцип устройства жидкостного термометра основан на расширении жидкостей при нагревании манометрического – на увеличении давления жидкостей и газов при их нагреве в замкнутых сосудах со-[фотивленйя – на изменении электрического сопротивления некоторых металлов при нагре-ва Нии.  [c.353]

Найти угловуЕО скорость о сосуда, при которой из него начнет выливаться жидкость. При этой угловой скорости определить силу давления Р жидкости на крышку К сосуда.  [c.101]

Формула (4.17) качественно правильно описывает и поведение жидкостей. В этом случае оба члена в правой ее части очень велики по сравнению с нормальными давлениями и вполне способны скомпенсировать друг друга. Для воды, например, константа А 10 К А , что дает при нормальных условиях для внутреннего давления, а/о, величину порядка 10 кбар. Все это соответствует тому, что жидкость, в принципе, может существовать, не оказывая никакого давления на стенки сосуда – при отсутствии силы тяжести, конечно. Иначе говоря, формула (4.17) позволяет ей иметь определенный объем и в отсутствии внещнего давления. Эта формула правильно отражает и слабую зависимость объема жидкости от давления при большой величине каждого из слагаемых в правой ее  [c.83]

Были, однако, случаи при некоторых температурах и определенных градиентах, когда уровень жидкости в сосуде явно поднимался выше уровня в ванне. С точки зрения температурной зависимости упругости пара это должно было бы означать, что при выделешги в резервуаре тепла температура содержащегося в нем голпя понижается, что совершенно абсурдно. Поэтому опыт был изменен теперь верх сосуда оставался открытым и, следовательно, не существовало разницы в давлении пара. Повторение того же самого эксперимента с протеканием тепла через капилляр в новых условиях (фиг. 8) дало поразительные результаты, а именно при выделении тепла уровень жидкости в резервуаре поднимался выше уровня в ванне. Авторам удалось значительно усилить этот эффект, нагревая светом трубку, плотно забитую наждачным порошком. Верхняя часть трубки оканчивалась узким соплом, выступающим из гелиевой ванны. В этих условиях свободная струя жидкого гелия поднималась на высоту 30 сл1 над уровнем жидкости в ванне.  [c.791]

Открытие термомехаиического эффекта сразу навело на мысль о возможности суш,ествования другого явления, противоположного ему в термодинамическом отношении. Термомеханический аффект показывает, что установление в жидком Не II разности температур вызывает появление разности давлений. Возникает вопрос, будет ли разность давлений вызывать соответствуюп1,ую разность температур. Этот механокалорический эффект был исследован в 1939 г. в Оксфорде Доунтом и Мендельсоном [18] (фиг. 9 и 10), установившими, что течение Не II от более высокого уровня к более низкому действительно сопровождается появлением градиента температуры. Эксперимент был проведен в маленьком дьюаровском сосуде, полностью закрытом, за исключением небольшого отверстия внизу (см. фиг. 9). Нижняя часть сосуда была заполнена плотно спрессованным крокусом, образую-ш,им пробку Р, со множеством тончайших каналов. Над пробкой укреплялся термометр Т. При частичном погружении сосуда в ванну с жидким Не II уровень жидкости внутри сосуда устанавливался на той же высоте, что и уровень в ванне, при этом температура жидкости внутри и снаружи была одинаковой. При приподнимании дьюаровского сосуда из ванны было видно.  [c.792]

Примечание. К этому же самому уравнению равновесия жидкости можно прийти при следующих условиях. Представим себе замкнутый сосуд произвольной формы, из которого выведены две цилиндрические трубки А и В с сечениями шд и Допустим, что сосуд заполнен жи/костью, на которую не действуют никакие непосредственно приложенные силы, и что трубки закрыты двумя поршнями Д и В, нд которые действуют нормальные давления Яц и Р . Если поршень А вдвинуть на бесконечно малую величину ц, то внутренний объем уменьшится на ЕдШо необходимо, следовательно, чтобы поршень В поднялся на такую величину 1, что овозможных работ Яд и Я , очевидно, равна Яд д – Я1Е1, то имеем уравнение равновесия  [c.227] Беседы о механике Изд4 (1950) — [ c.0 ]

Источник