Жидкость принимает форму сосуда

Основным отличием жидкостей от твердых (упругих) тел является способность легко изменять свою форму. Части жидкости могут свободно сдвигаться, скользя друг относительно друга. Поэтому жидкость принимает форму сосуда, в который она налита. В жидкость, как и в газообразную среду, можно погружать твердые тела. В отличие от газов жидкости практически несжимаемы.

На тело, погруженное в жидкость или газ, действуют силы, распределенные по поверхности тела. Для описания таких распределенных сил вводится новая физическая величина – давление.

Давление определяется как отношение модуля силы действующей перпендикулярно поверхности, к площади S этой поверхности:

В системе СИ давление измеряется в паскалях (Па):

Часто используются внесистемные единицы: нормальная атмосфера (атм) и миллиметр ртутного столба (мм Hg):

1 атм = 101325 Па = 760 мм Hg.

Французский ученый Блез Паскаль в середине XVII века эмпирически установил закон, названный законом Паскаля:

Давление в жидкости или газе передается во всех направлениях одинаково и не зависит от ориентации площадки, на которую оно действует.

Для иллюстрации закона Паскаля на рис. 1.15.1 изображена небольшая прямоугольная призма, погруженная в жидкость. Если предположить, что плотность материала призмы равна плотности жидкости, то призма должна находиться в жидкости в состоянии безразличного равновесия. Это означает, что силы давления, действующие на грани призмы, должны быть уравновешены. Это произойдет только в том случае, если давления, т. е. силы, действующие на единицу площади поверхности каждой грани, одинаковы: p1 = p2 = p3 = p.

Рисунок 1.15.1. Закон Паскаля: p1 = p2 = p3 = p

Давление жидкости на дно или боковые стенки сосуда зависит от высоты столба жидкости. Сила давления на дно цилиндрического сосуда высоты h и площади основания S равна весу столба жидкости mg, где m = ρghS – масса жидкости в сосуде, ρ – плотность жидкости. Следовательно

Такое же давление на глубине h в соответствии с законом Паскаля жидкость оказывает и на боковые стенки сосуда. Давление столба жидкости ρgh называют гидростатическим давлением.

Если жидкость находится в цилиндре под поршнем (рис. 1.15.2), то действуя на поршень некоторой внешней силой можно создавать в жидкости дополнительное давление p0 = F / S, где S – площадь поршня.

Таким образом, полное давление в жидкости на глубине h можно записать в виде:

Если на рис. 1.15.2 поршень убрать, то давление на поверхность жидкости будет равно атмосферному давлению: p0 = pатм.

Рисунок 1.15.2. Зависимость давления от высоты столба жидкости

Из-за разности давлений в жидкости на разных уровнях возникает выталкивающая или архимедова сила

Рис. 1.15.3 поясняет появление архимедовой силы. В жидкость погружено тело в виде прямоугольного параллелепипеда высотой h и площадью основания S. Разность давлений на нижнюю и верхнюю грани есть:

Поэтому выталкивающая сила будет направлена вверх, и ее модуль равен

где V – объем вытесненной телом жидкости, а ρV – ее масса.

Архимедова сила, действующая на погруженное в жидкость (или газ) тело, равна весу жидкости (или газа), вытесненной телом. Это утверждение, называемое законом Архимеда, справедливо для тел любой формы. (Тело впернутое в воду выпирает на свободу силой выпертой воды телом впернутым туды! так легче запомнить)

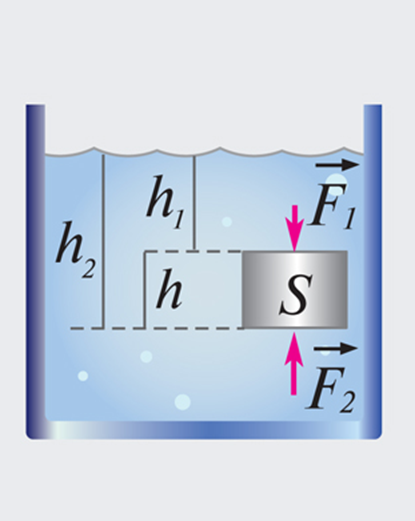Рисунок 1.15.3. Архимедова сила. FА = F2 – F1 = S(p2 – p1) = ρgSh, F1 = p1S, F2 = p2S

Из закона Архимеда вытекает, что если средняя плотность тела ρт больше плотности жидкости (или газа) ρ, тело будет опускаться на дно. Если же ρт < ρ, тело будет плавать на поверхности жидкости.

Тут можно и разобраться с вопросом «Почему корабль не тонет, он же железный?» Объем воды измещенной кораблем по весу больше веса корабля. Одна из основных характеристик судов так и называется – водоизмещение.

Объем погруженной части тела будет таков, что вес вытесненной жидкости равен весу тела. Для подъема воздушного шара в воздухе его вес должен быть меньше веса вытесненного воздуха. Поэтому воздушные шары заполняют легкими газами (водородом, гелием) или нагретым воздухом.

Из выражения для полного давления в жидкости p = p0 + ρgh вытекает, что в сообщающихся сосудах любой формы, заполненных однородной жидкостью, давления в любой точке на одном и том же уровне одинаковы (рис. 1.15.4).

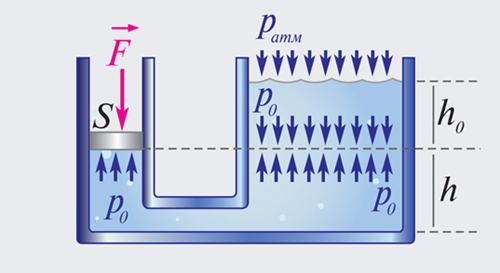Рисунок 1.15.4. Пример сообщающихся сосудов. В правом сосуде поверхность жидкости свободна. На уровне h давление в обоих сосудах одинаково и равно p0 = F / S = ρgh0 + pатм. Давление на дно сосудов p = p0 + ρgh

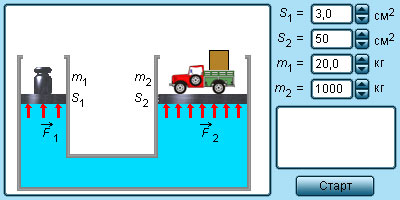
Если оба вертикально расположенных цилиндра сообщающихся сосудов закрыть поршнями, то с помощью внешних сил, приложенных к поршням, в жидкости можно создать большое давление p, во много раз превышающее гидростатическое давление ρgh в любой точке системы. Тогда можно считать, что во всей системе устанавливается одинаковое давление p. Если поршни имеют разные площади S1 и S2, то на них со стороны жидкости действуют разные силы F1 = pS1 и F2 = pS2. Такие же по модулю, но противоположно направленные внешние силы должны быть приложены к поршням для удержания системы в равновесии. Таким образом,

Если S2 >> S1, то F2 >> F1. Устройства такого рода называют гидравлическими машинами (рис. 1.15.5). Они позволяют получить значительный выигрыш в силе. Если поршень в узком цилиндре переместить вниз под действием внешней силы на расстояние то поршень в широком цилиндре переместится на расстояние

поднимая тяжелый груз.

Таким образом, выигрыш в силе в n раз обязательно сопровождается таким же проигрышем в расстоянии. При этом произведение силы на расстояние остается неизменным:

Это правило выполняется для любых идеальных машин, в которых не действуют силы трения. Оно называется «золотым правилом механики».

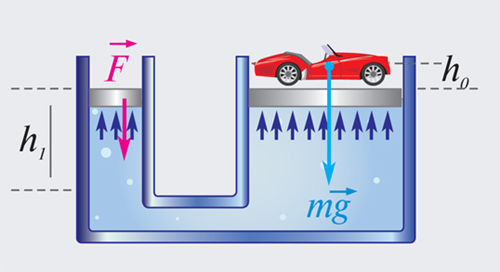Рисунок 1.15.5. Гидравлическая машина.

Гидравлические машины, используемые для подъема грузов, называются домкратами. Они широко применяются также в качестве гидравлических прессов. В качестве жидкости обычно используются минеральные масла.

Модель. Гидравлическая машина.

Еще статьи в этой категории:

• Условия равновесия тел

Источник

В этом состоянии сохраняется объем, но не сохраняется форма. Например, если перелить молоко из кувшина в стакан – молоко, имевшее форму кувшина, примет форму стакана. Кстати, в корове у молока тоже была другая форма.

Расстояние между молекулами в жидком состоянии чуть больше, чем в твердом, но все равно невелико. При этом частицы не собраны в кристаллическую решетку, а расположены хаотично. Молекулы почти не двигаются, но при нагревании жидкости делают это более охотно.

Вспомните, что происходит, если залить чайный пакетик холодной водой – он почти не заваривается. А вот если налить кипяточку – чай точно будет готов.

Агрегатных состояния точно три?

На самом деле, есть еще четвертое – плазма. Звучит, как что-то из научной фантастики, но это просто ионизированный газ – газ, в котором помимо нейтральных частиц, есть еще и заряженные. Ионизаторы воздуха как раз строятся на принципе перехода из газообразного вещества в плазму.

Сообщающиеся сосуды

Поскольку жидкость принимает форму сосуда, в который ее поместили, имеет место быть такое явление, как сообщающиеся сосуды.

• Сообщающиеся сосуды – это сосуды, соединенные между собой ниже уровня жидкости (в каждом сосуде). Так жидкость может перемещаться из одного сосуда в другой.

Какую бы форму не имели такие сосуды, на поверхности однородных жидкостей в состоянии покоя на одном уровне действует одинаковое давление.

Если в колена сообщающихся сосудов налить жидкости, плотности которых будут различны, то меньший объём более плотной жидкости в одном колене уравновесит больший объём менее плотной жидкости в другом колене сосуда.

Другими словами, высота столба жидкости с меньшей плотностью больше, чем высота столба жидкости с большей плотностью. Давайте рассчитаем, во сколько высота столба жидкости с меньшей плотностью больше высоты столба жидкости с большей плотностью, если эти две несмешивающиеся жидкости находятся в сообщающихся сосудах.

p = ρgh, p1 = p2, ρ1 gh1= ρ2 gh2,

Отсюда:

h1/h2 = ρ1/ρ2

ρ2 = (h1/h2) * ρ1

Применение сообщающихся сосудов

На принципе сообщающихся сосудов основано устройство очень простого прибора для определения плотности жидкости. Этот прибор состоит из двух сообщающихся сосудов: двух вертикальных стеклянных трубок, соединенных между собой третьей изогнутой трубкой.

Одна из вертикальных трубок заполняется жидкостью, плотность которой нужно определить, а другая – жидкостью известной плотности (например, водой, плотность которой равна 1000 кг/м^3). Жидкости должны заполнить трубки настолько, чтобы их уровень в изогнутой трубке посередине был на отметке прибора 0. Высоты жидкостей в трубках над этой отметкой измеряют и находят плотность исследуемой жидкости, зная, что высоты обратно пропорциональны плотностям (об этом мы говорили выше).

Также на законе сообщающихся сосудах основаны устройства, которые определяют уровень жидкости в закрытых сосудах: резервуарах, паровых котлах.

Чтобы судно могло переплыть из одной водного бассейна в другой, если уровни воды в них разные, необходимо использовать шлюз. Устройство шлюза также основано на принципе сообщающихся сосудов. В первых воротах шлюза открывается клапан, камера соединяется с водоёмом, они становятся сообщающимися сосудами, уровни воды в них выравниваются. После этого ворота открываются, и судно проходит в первую камеру. Открывается следующий клапан, после выравнивания уровней воды открываются ворота, и так повторяется столько раз, сколько камер имеет шлюз.

Давление столба жидкости

Выведем формулу давления столба жидкости через основную формулу давления.

Давление

p = F/S

p – давление [Па]

F – сила [Н]

S – площадь [м^2]

В случае давления жидкости на дно сосуда мы можем заменить силу в формуле на силу тяжести.

p = mg/S

Также мы можем представить массу жидкости, как произведение плотности на объем:

p = ρ*V*g/S

Из геометрии мы знаем, что объем тела вращения (например, цилиндра) – это произведение площади основания на высоту: V = Sh.

Следовательно, высота будет равна h = V/S. Подставляем в формулу высоту вместо отношения объема к площади.

p = ρ*g*V/S

p = ρgh

В сообщающихся сосудах давление жидкости на одном уровне (на одной и той же высоте) будет одинаковым.

А можно сделать так, чтобы давление было разным?

С помощью перегородки можно сделать так, чтобы уровень жидкости, а следовательно, и давления в сообщающихся сосудах отличались.

Перегородка, установленная между сосудами перекроет сообщение. Далее доливая жидкость в один из сосудов мы создаем дополнительное давление. Если затем убрать перегородку, то жидкость начнет перетекать в тот сосуд, где её уровень ниже – до тех пор, пока высота жидкости в обоих сосудах не станет одинаковой.

Этот принцип используют в водонапорной башне. Чтобы создать высокое давление, башню наполняют водой. Затем открывают трубы на нижнем этаже, и вода устремляется в дома в наши краны и батареи.

Задачка

Какой площади необходимо сделать малый поршень в гидравлическом прессе, для того, чтобы выигрыш в силе получился равным 2? Площадь большого поршня равна 10 см^2.

Решение:

Гидравлический пресс – это два цилиндрических сообщающихся сосуда. Площадь большого поршня, с приложенной силой F1, равна 10 см^2.

Площадь малого поршня обозначим Sмал, к нему приложена сила F2.

Давления в сообщающихся сосудах на одинаковой высоте равны: p1 = p2

Подставим формулу давления:

F1/Sбол=F2/Sмал.

Выразим Sмал, получим:

Sмал = (F2/F1) * Sбол

Так как по условию выигрыш в силе F2/F1 равен 2, то:

Sмал=2*Sбол= 2*10 = 20 см^2

Ответ: малый поршень необходимо сделать с площадью равной 20 см^2

Понимать и любить этот мир гораздо проще, когда разбираешься в физике. В этом помогут небезразличные и компетентные преподаватели онлайн-школы Skysmart.

Чтобы формулы и задачки ожили и стали более дружелюбными, на уроках мы разбираем примеры из обычной жизни современных подростков. Приходите на бесплатный вводный урок по физике и начните учиться в удовольствие уже завтра!

Источник

Авторы: А. М. Емельяненко, Н. В. Чураев

КАПИЛЛЯ́РНЫЕ ЯВЛЕ́НИЯ, со­во­куп­ность яв­ле­ний, обу­слов­лен­ных по­верх­но­ст­ным на­тя­же­ни­ем на гра­ни­це раз­де­ла не­сме­ши­ваю­щих­ся сред (в сис­те­мах жид­кость – жид­кость, жид­кость – газ или пар) при на­ли­чии ис­крив­ле­ния по­верх­но­сти. Ча­ст­ный слу­чай по­верх­но­ст­ных яв­ле­ний.

Рис. 1.

При от­сут­ст­вии си­лы тя­же­сти жид­кость ог­ра­ни­чен­ной мас­сы под воз­дей­ст­ви­ем по­верх­но­ст­но­го на­тя­же­ния стре­мит­ся за­нять объ­ём с ми­ним. по­верх­но­стью, т. е. при­ни­ма­ет фор­му ша­ра. В ус­ло­ви­ях дей­ст­вия си­лы тя­же­сти не слиш­ком вяз­кая жид­кость дос­та­точ­ной мас­сы при­ни­ма­ет фор­му со­су­да, в ко­то­рый на­ли­та, и её сво­бод­ная по­верх­ность при от­но­си­тель­но боль­шой пло­ща­ди (вда­ли от сте­нок со­су­да) ста­но­вит­ся пло­ской, т. к. роль по­верх­но­ст­но­го на­тя­же­ния ме­нее су­ще­ст­вен­на, чем си­лы тя­же­сти. При взаи­мо­дей­ст­вии с по­верх­но­стью др. жид­ко­сти или твёр­до­го те­ла (напр., со стен­ка­ми со­су­да) по­верх­ность рас­смат­ри­вае­мой жид­ко­сти ис­крив­ля­ет­ся в за­ви­си­мо­сти от на­ли­чия или от­сут­ст­вия сма­чи­ва­ния. Ес­ли име­ет ме­сто сма­чи­ва­ние, т. е. мо­ле­ку­лы жид­ко­сти 1 (рис. 1) силь­нее взаи­мо­дей­ст­ву­ют с мо­ле­ку­ла­ми по­верх­но­сти 3, чем с мо­ле­ку­ла­ми др. жид­ко­сти (или га­за) 2, то под воз­дей­ст­ви­ем раз­но­сти сил меж­мо­ле­ку­ляр­но­го взаи­мо­дей­ст­вия жид­кость 1 под­ни­ма­ет­ся по стен­ке со­су­да – уча­сток жид­ко­сти, при­мы­каю­щий к стен­ке, ис­крив­ля­ет­ся. Дав­ле­ние, вы­зы­вае­мое подъ­ё­мом жид­ко­сти, урав­но­ве­ши­ва­ет­ся ка­пил­ляр­ным дав­ле­ни­ем $Delta p$ – раз­но­стью дав­ле­ний над и под ис­крив­лён­ной по­верх­но­стью раз­де­ла. Ве­ли­чи­на ка­пил­ляр­но­го дав­ле­ния за­ви­сит от сред­не­го ра­диу­са $r$ кри­виз­ны по­верх­но­сти и оп­ре­де­ля­ет­ся фор­му­лой Ла­п­ла­са: $Delta p=2 sigma/r$, где $sigma$ – по­верх­но­ст­ное на­тя­же­ние. Ес­ли гра­ни­ца раз­де­ла фаз пло­ская ($r= infty$), то в ус­ло­ви­ях ме­ха­нич. рав­но­ве­сия сис­те­мы дав­ле­ния с обе­их сто­рон гра­ни­цы раз­де­ла рав­ны и $Delta p=0$. В слу­чае во­гну­той по­верх­но­сти жид­ко­сти ($r lt 0$) дав­ле­ние в жид­ко­сти ни­же, чем дав­ле­ние в гра­ни­ча­щей с ней фа­зе и $Delta p lt 0$; для вы­пук­лой по­верх­но­сти ($r>0$) $Delta p>0$.

Ес­ли стен­ки со­су­да при­бли­зить друг к дру­гу, зо­ны ис­крив­ле­ния по­верх­но­сти жид­ко­сти об­ра­зу­ют ме­ниск – пол­но­стью ис­крив­лён­ную по­верх­ность. Об­ра­зо­вав­шая­ся сис­те­ма на­зы­ва­ет­ся ка­пил­ля­ром; в нём в ус­ло­ви­ях сма­чи­ва­ния дав­ле­ние под ме­ни­ском по­ни­же­но и жид­кость в ка­пил­ля­ре под­ни­ма­ет­ся (над уров­нем сво­бод­ной по­верх­но­сти жид­ко­сти в со­су­де); вес стол­ба жид­ко­сти вы­со­той $h$ урав­но­ве­ши­ва­ет ка­пил­ляр­ное дав­ле­ние $Delta p$. Не­сма­чи­ваю­щая жид­кость в ка­пил­ля­ре об­ра­зу­ет вы­пук­лый ме­ниск, дав­ле­ние над ко­то­рым вы­ше, и жид­кость в нём опус­ка­ет­ся ни­же уров­ня сво­бод­ной по­верх­но­сти вне ка­пил­ля­ра. Вы­со­та под­ня­тия (опус­ка­ния) жид­ко­сти в ка­пил­ля­ре от­но­си­тель­но сво­бод­ной по­верх­но­сти (где $r= infty$ и $Delta p=0$) оп­ре­де­ля­ет­ся со­от­но­ше­ни­ем: $h=2 sigma cos theta/ Delta rho gr$, где $theta$ – крае­вой угол (угол ме­ж­ду ка­са­тель­ной к по­верх­но­сти ме­ни­ска и стен­кой ка­пил­ля­ра), $Delta rho$ – раз­ность плот­но­стей жид­ко­сти 1 в ка­пил­ля­ре и внеш­ней сре­ды 2, $g$ – ус­ко­ре­ние сво­бод­но­го па­де­ния.

Ис­крив­ле­ние по­верх­но­сти влия­ет на ус­ло­вия рав­но­ве­сия ме­ж­ду жид­ко­стью и её на­сы­щен­ным па­ром: со­глас­но Кель­ви­на урав­не­нию, дав­ле­ние па­ров над ка­п­лей жид­ко­сти по­вы­ша­ет­ся с умень­ше­ни­ем её ра­диу­са, что объ­яс­ня­ет, напр., рост боль­ших ка­пель в об­ла­ках за счёт ма­лых.

Рис. 2.

К ха­рак­тер­ным К. я. от­но­сят­ся ка­пил­ляр­ное впи­ты­ва­ние, по­яв­ле­ние и рас­про­стра­не­ние ка­пил­ляр­ных волн, ка­пил­ляр­ное пе­ре­дви­же­ние жид­ко­сти, ка­пил­ляр­ная кон­ден­са­ция, про­цес­сы ис­па­ре­ния и рас­тво­ре­ния при на­ли­чии ис­крив­лён­ной по­верх­но­сти. Ка­пил­ляр­ное впи­ты­ва­ние ха­рак­те­ри­зу­ет­ся ско­ро­стью, за­ви­ся­щей от ка­пил­ляр­но­го дав­ле­ния и вяз­ко­сти жид­ко­сти. Оно иг­ра­ет су­ще­ст­вен­ную роль в во­до­снаб­же­нии рас­те­ний, дви­же­нии во­ды в поч­вах и др. про­цес­сах, свя­зан­ных с дви­же­ни­ем жид­ко­стей в по­рис­тых сре­дах. Ка­пил­ляр­ная про­пит­ка – один из рас­про­стра­нён­ных про­цес­сов хи­мич. тех­но­ло­гии. В сис­те­мах с не­па­рал­лель­ны­ми стен­ка­ми (или ка­пил­ля­рах ко­нич. се­че­ния) кри­виз­на ме­ни­сков за­ви­сит от рас­по­ло­же­ния в них гра­нич­ных по­верх­но­стей жид­ко­сти, и ка­п­ля сма­чи­ваю­щей жид­ко­сти в них на­чи­на­ет дви­гать­ся к ме­ни­ску с мень­шим ра­диу­сом (рис. 2), т. е. в ту сто­ро­ну, где дав­ле­ние ни­же. При­чи­ной ка­пил­ляр­но­го пе­ре­дви­же­ния жид­ко­сти мо­жет слу­жить и раз­ни­ца сил по­верх­но­ст­но­го на­тя­же­ния в ме­ни­сках, напр. при су­ще­ст­во­ва­нии гра­ди­ен­та темп-ры или при ад­сорб­ции по­верх­но­ст­но-ак­тив­ных ве­ществ, сни­жаю­щих по­верх­но­ст­ное на­тя­же­ние.

Ка­пил­ляр­ной кон­ден­са­ци­ей на­зы­ва­ют про­цесс кон­ден­са­ции па­ра в ка­пил­ля­рах и мик­ро­тре­щи­нах по­рис­тых тел, а так­же в про­ме­жут­ках ме­ж­ду сбли­жен­ны­ми твёр­ды­ми час­ти­ца­ми или те­ла­ми. Не­об­хо­ди­мое ус­ло­вие ка­пил­ляр­ной кон­ден­са­ции – на­ли­чие сма­чи­ва­ния по­верх­но­сти тел (час­тиц) кон­ден­си­рую­щей­ся жид­ко­стью. Про­цес­су ка­пил­ляр­ной кон­ден­са­ции пред­ше­ст­ву­ет ад­сорб­ция мо­ле­кул па­ра по­верх­но­стью тел и об­ра­зо­ва­ние ме­ни­сков жид­ко­сти. В ус­ло­ви­ях сма­чи­ва­ния фор­ма ме­ни­сков во­гну­тая и дав­ле­ние $p$ на­сы­щен­но­го па­ра над ни­ми ни­же, чем дав­ле­ние на­сы­щен­но­го па­ра $p_0$ при тех же ус­ло­ви­ях над пло­ской по­верх­но­стью. Т. е. ка­пил­ляр­ная кон­ден­са­ция про­ис­хо­дит при бо­лее низ­ких, чем $p_0$, дав­ле­ни­ях.

Ис­крив­ле­ние по­верх­но­сти жид­ко­сти мо­жет су­ще­ст­вен­но вли­ять на про­цес­сы ис­па­ре­ния, ки­пе­ния, рас­тво­ре­ния, за­ро­ды­ше­об­ра­зо­ва­ния при кон­ден­са­ции па­ра и кри­стал­ли­за­ции. Так, свой­ст­ва сис­тем, со­дер­жа­щих боль­шое ко­ли­че­ст­во ка­пель или пу­зырь­ков га­за (эмуль­сий, аэ­ро­зо­лей, пен), и их фор­ми­ро­ва­ние во мно­гом оп­ре­де­ля­ют­ся К. я. Они ле­жат так­же в ос­но­ве мн. тех­но­ло­гич. про­цес­сов: фло­та­ции, спе­ка­ния по­рош­ков, вы­тес­не­ния неф­ти из пла­стов вод­ны­ми рас­тво­ра­ми по­верх­но­ст­но-ак­тив­ных ве­ществ, ад­сорб­ци­он­но­го раз­де­ле­ния и очи­ст­ки га­зо­вых и жид­ких сме­сей и т. п.

Впер­вые К. я. бы­ли ис­сле­до­ва­ны Ле­о­нар­до да Вин­чи. Сис­те­ма­тич. на­блю­де­ния и опи­са­ния К. я. в тон­ких труб­ках и ме­ж­ду пло­ски­ми, близ­ко рас­по­ло­жен­ны­ми стек­лян­ны­ми пла­сти­на­ми про­вёл в 1709 Ф. Хокс­би, де­мон­ст­ра­тор Лон­дон­ско­го ко­ро­лев­ско­го об-ва. Ос­но­вы тео­рии К. я. за­ло­же­ны в тру­дах Т. Юн­га, П. Ла­п­ла­са, а их тер­мо­ди­на­мич. рас­смот­ре­ние осу­ще­ст­вил Дж. Гиббс (1876).

Источник