Жидкость в сосуде движущемся с постоянной ускорением
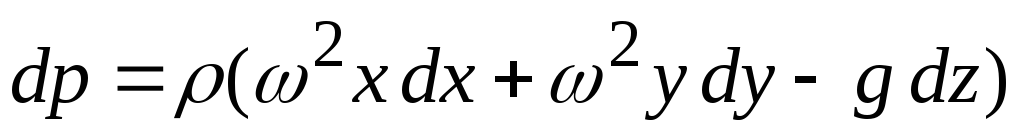
В зависимости от характера действующих массовых сил поверхность равного давления в жидкости, как и свободная поверхность, может принимать различную форму. Ниже рассматриваются некоторые случаи равновесия жидкости в движущихся сосудах.
1. Жидкость находится в сосуде, который движется в горизонтальном направлении с постоянным ускорением ±а (знак плюс соответствует ускорению сосуда, знак минус – замедлению ) (см. рисунок).
В данном случае жидкость подвержена воздействию не только поверхностных сил, но также массовых сил тяжести и инерции. Поверхность равного давления является наклонной плоскостью. Давление в любой точке жидкости определяется по формуле
p = p0 + ρ·(g·z ± a·x),
Для свободной поверхности жидкости, когда р=p0, уравнение принимает вид:
g·z = ± a·x
или
z/x = tg α = ± a/g,
где α – угол наклона свободной поверхности жидкости к горизонту.
Последнее приведенное выше выражение позволяет определять (при условии, чтобы жидкость не переливалась через задний борт сосуда длиной l) высоту борта h при заданном значении а или предельное ускорение а при заданном значении h.
Если сосуд движется равномерно (а = 0), уравнение приводим к виду:
p = p0 + ρ·g·z = p0·γ
В этом случае поверхность равного давления представляет горизонтальную плоскость.
2. Жидкость находится в открытом цилиндрическом сосуде, который вращается вокруг вертикальной оси с постоянной угловой скоростью ω.
В данном случае жидкость подвержена воздействию не только поверхностных сил, но также массовых сил тяжести и центробежной.
Поверхность равного давления представляет параболоид вращения. Распределение давления в жидкости по глубине определяется выражением:
p = p0 + γ·((ω2·r2)/(2·g) – z)
Для любой точки свободной поверхности жидкости, когда p = p0, уравнение принимает вид:
z = (ω2·r2)/(2·g) = u2/(2·g),
где окружная скорость u = ω·r (r – радиус вращения точки).
Высота параболоида вращения:
h = ω2·r20/(2·g),
где r0 – радиус цилиндрического сосуда.
Сила давления жидкости на дно сосуда:
P = γ·π·r20·h0 = γ·π·r20·(h1 + h/2),
где h0 – начальная глубина жидкости в сосуде до момента его вращения.
Давление на боковую стенку сосуда изменяется по линейному закону. Эпюра давления представляет прямоугольный треугольник ACD с высотой h1 + h и основанием γ·(h1 + h).
3. Жидкость находится в цилиндрическом сосуде, который вращается вокруг горизонтальной оси с постоянной угловой скоростью ω.
В данном случае жидкость также подвержена воздействию массовых сил тяжести и центробежной.
Поверхности равного давления представляют концентрически расположенные боковые поверхности цилиндров, оси которых горизонтальны и смещены относительно оси оу на величину эксцентриситета e = g/ω2 (см. рисунок а).
При большом числе оборотов сосуда влияние силы тяжести по сравнению с влиянием центробежной силы становится незначительным, и, следовательно, величиной эксцентриситета е можно пренебречь. Тогда поверхности равного давления становятся концентрическими цилиндрами, оси которых совпадают с осью сосуда (см. рисунок б).
Распределение давления по глубине жидкости определяется выражением:
p = p0 + γ·ω2·(r2 – r20)/(2·g)
где p и p0 – соответственно давления в точках цилиндрических поверхностей с радиусами r и r0.
Данное уравнение справедливо и тогда, когда сосуд радиусом r лишь частично заполнен жидкостью. Свободная поверхность жидкости в этом случае также будет цилиндрической с радиусом r0 и давлением во всех ее точках р0.
Как видно из последнего уравнения, закон распределения давления по радиусу является параболическим. Эпюра давления представленная на рисунке в. Такие приближенные решения могут применяться при любом положении оси вращения сосуда, однако при условии большого числа его оборотов.
Вильнер Я.М. Справочное пособие по гидравлике, гидромашинам и гидроприводам.
Источник
вующая массовая сила всегда действует нормально к поверхности уровня. Выбирая систему координат, жестко связанную со стенками сосуда, приходим к статической задаче, основой для решения которой служит диф-
ференциальное уравнение равновесия жидкости:
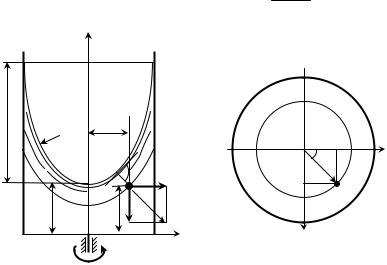
dp = ρ(Xdx + Ydy + Zdz), | (2.1) |
где x, y, z – координаты точек жидкости в системе отсчета, связанной с сосудом; p – давление в жидкости; ρ – плотность жидкости;
X, Y, Z – проекции единичной массовой силы на координатные оси.
Для определения формы поверхности уровня и характера распределения давления в этом сосуде следует в число действующих массовых сил включить также силы инерции.
Существуют два состояния относительного покоя жидкости:
-в сосуде, движущемся прямолинейно и равноускоренно;
-в сосуде, равномерно вращающемся вокруг вертикальной оси.
Сосуд с жидкостью движется с ускорением a вдоль прямой, накло-
z
z0
0(y)
α
Рис. 2.1. Относительное равновесие жидкости при прямолинейном равноускоренном движении сосуда
ненной к горизонту под углом α (рис. 2.1).
К массовым силам наряду с силой тяжести в данном случае относится еще и сила инерции j = – a, направленная противоположно ускорению сосуда. В системе координат (рис. 2.1) проекции единичных массовых сил будут равны
X = j – g sin α ; Y = 0 ; Z = – g cos α.
Подставляя эти выражения в уравнение равновесия (2.1), получаем
dp = ρ [(j – g sin α)dx – g cos α dz], | (2.2) |
а после интегрирования
p = ρ (j – g sin α) x – ρ g cos αz + C,
20
z − z0 =
где С – постоянная интегрирования, определяемая из граничных условий на свободной поверхности при x = 0, z = z0 и p = p0.
После подстановки граничных условий получаем закон распределения давления:
p = р0+ρ(j – g sin α) x +ρ g cos α (z0 – z). (2.3)
Так как на поверхности уровня давление одинаково в любой ее точке, полагая в уравнении (2.2) p = const, получаем уравнение поверхностей уровня
ρ( j – g sin α) x – ρ g cos α z + C1 = 0. | (2.4) |
Уравнение (2.4) дает семейство плоскостей, параллельных оси Y. Одной из этих плоскостей является свободная поверхность.
Подставляя в формулу (2.4) граничные условия x = 0 и z = z0, нахо-
дим
C1 = ρ g z0 cos α.
Уравнение свободной поверхности имеет вид
j − g sinα x , (2.5) g cosα
где | j − g sinα | = tgθ . |
g cosα | ||
2.3. Равновесие жидкости в цилиндрическом сосуде, равномерно вращающемся вокруг вертикальной оси
Равновесие жидкости в сосуде, вращающемся вокруг вертикальной оси, реализуется лишь при постоянной угловой скорости вращения ω = const (рис. 2.2).
По истечении достаточного времени после начала вращения жидкость приобретает ту же скорость вращения, что и сосуд, а свободная поверхность ее видоизменяется: в центральной части уровень жидкости понизится, у стенок – повысится и вся свободная поверхность станет некоторой поверхностью вращения (рис.2.2, а). На жидкость в этом случае будут действовать две массовые силы: сила тяжести и центробежная сила, кото-
рые, будучи отнесенными к единице массы, соответственно равны g и ω²r. При проецировании на оси координат равнодействующей массовых
сил (рис.2.2, б) получим выражения
X = ω2 r cos α= ω2 x ;Y = ω2 r sin α = ω2 y ; Z = – g.
Подставляя эти выражения в уравнение (2.1), получаем dp = ρ(ω2xdx +ω2ydy – gdz),
или
dp = ρ(ω2rdr – g dz).
21
После интегрирования находим | |||
p =с | щ2 r 2 | −сg z +C . | (2.6) |
2 | |||
Подставляя в уравнение (2.6) граничные условия r = 0, z = z0 и p = p0, | |||
находим постоянную интегрирования | |||
C = р0 + ρ g z0. | |||
Тогдазаконраспределениядавленияможновыразитьформулой | |||
p = p0 +сщ2r2 +сg(z0 − z) , | (2.7) | ||
2 | |||
т. е. в этом случае также справедлив линейный закон распределения давления по глубине. Изменение давления по радиусу подчиняется параболическому закону. Полагая p = const, из выражения (2.6) получим уравнение поверхностей уровня:
p =с | щ2 r 2 | −сgz +C1 . | (2.8) | |
2 | ||||
z | ||||
H | r | |||
p0 | O | |||
ω2r | r α y | x | ||
x | ||||
g | j | |||
z | ||||
O | x | y | ||
ω=const | ||||
а | б | |||
Рис. 2.2. Относительное равновесие жидкости в равномерно | ||||
вращающемся цилиндрическом сосуде | ||||
Эти поверхности уровня представляют собой параболоиды вращения. Одним из таких параболоидов является свободная поверхность жидкости.
Так как в вершине параболоида свободной поверхности r = 0, z = z0,
C1 = ρg z0 ,то уравнение свободной поверхности примет вид | ||||||
z − z0 | = | щ2 r 2 | . | (2.9) | ||
2g | ||||||
Зависимость | щ2 r 2 | |||||
z − z0 | = | h = | (2.10) | |||
2g | ||||||
при постоянном радиусе (r = const) устанавливает связь между величиной возвышения h любой точки, расположенной на свободной поверхности
над точкой, лежащей на оси вращения, и угловой скоростью ω. Она позволяет определить число оборотов цилиндра, если известно превышение h , что и используется при конструировании жидкостных тахометров, с помо-
22
Источник
05-3
Относительный покой жидкости в сосуде, движущемся с постоянным ускорением
и вращающемся вокруг вертикальной оси с постоянной угловой скоростью
Относительный покой (равновесие жидкости в движущемся сосуде)
При равновесии в движущемся сосуде жидкость движется вместе с сосудом как единое целое, т.е. находится в состоянии относительного покоя.
Сосуд, движущийся горизонтально и прямолинейно с постоянным ускорением
Рассмотрим равновесие жидкости, находящейся в сосуде, перемещающемся горизонтально с постоянным положительным ускорением 
.
|
В том случае из массовых сил действуют сила тяжести 
и сила инерции 
, направление которой противоположно направлению ускорения.
Проекция плотности распределения силы тяжести 
, а силы инерции 
.
Применим уравнение равновесия жидкости Эйлера в объединенном виде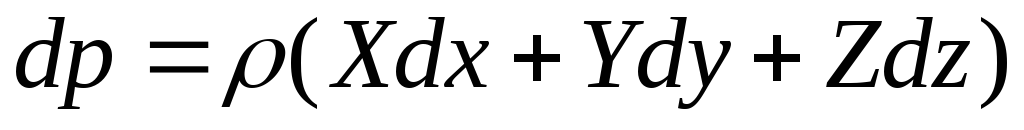 
После интегрирования 
При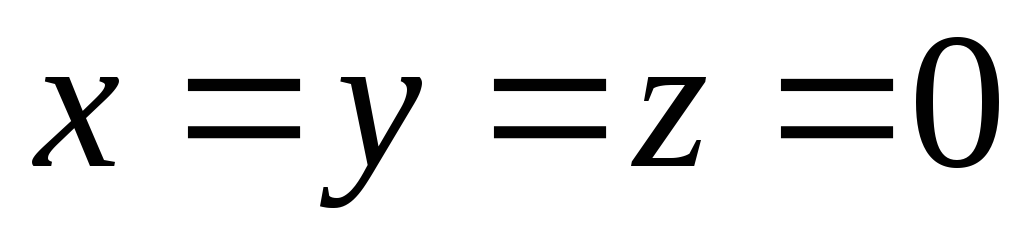 
имеем 
, окончательно 
.
Уравнение поверхностей равного давления из условия 
получим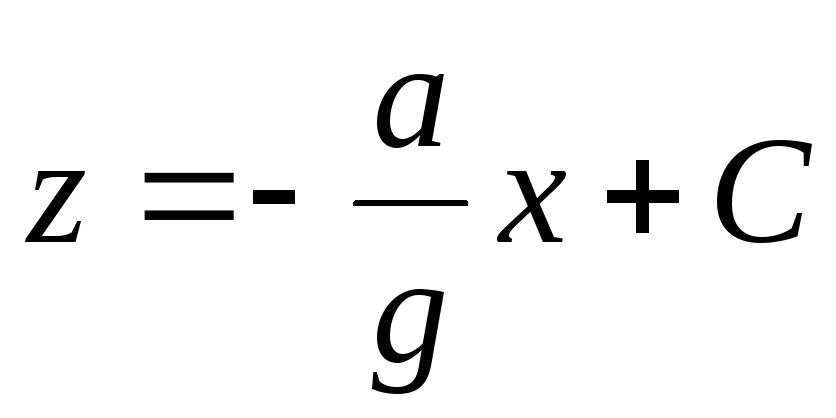
. Для свободной поверхности 
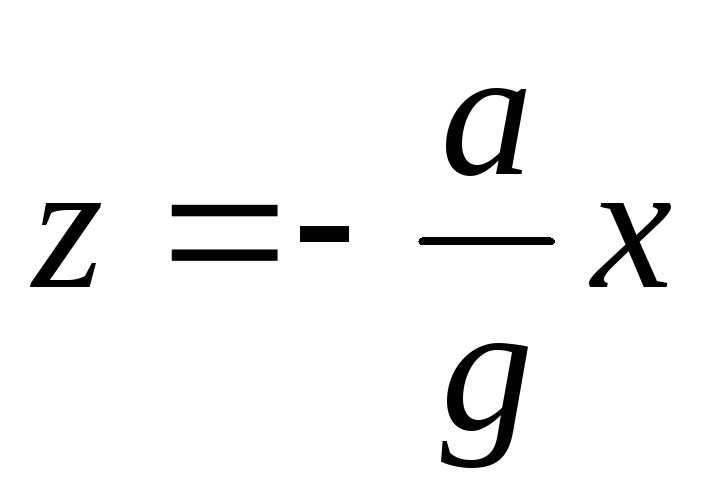. Тангенс угла наклона поверхностей равного давления 
(не зависит от 
).
Как распределено давление по глубине ? Обозначим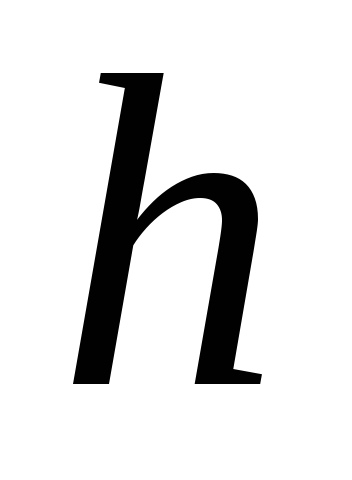 
– глубину точки, отсчитанную по вертикали от свободной поверхности. Тогда 
. Подставим в выражение для давления 
. Распределение давления по глубине подчиняется гидростатическому закону.
Сосуд, движущийся вертикально с постоянным ускорением
В этом случае положительные значения ускорения 
соответствуют ускорению, направленному вверх (по оси 
), а отрицательные -когда ускорение направлено вниз.
Уравнение поверхностей равного давления 
.
Давление 
.
Цилиндрический сосуд, равномерно вращающийся относительно вертикальной оси
| Рассмотрим цилиндрический сосуд, заполненный до некоторого уровня жидкостью плотностью На элементарную массу Ее проекции на оси координат (из подобия треугольников)
|
и приведенный во вращение с постоянной угловой скоростью 
относительно вертикальной оси. Через некоторое время после начала вращения сосуда жидкость под действием сил трения будет вращаться с той же скоростью, что и сосуд.
, расположенную от оси на расстоянии 
, действуют силы веса 
и центробежная сила инерции, направленная вдоль радиуса и равная 
.
, 
Проекции вектора плотности распределения массовых сил при этом:
от силы тяжести 
, 
, 
от центробежной силы инерции 
, 
, 
.
Применим уравнение равновесия жидкости Эйлера в объединенном виде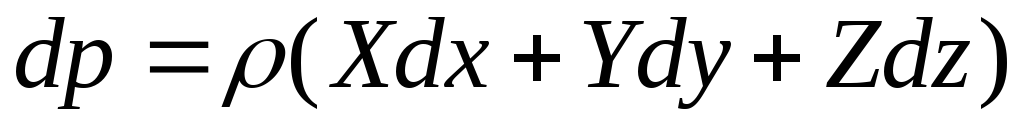 
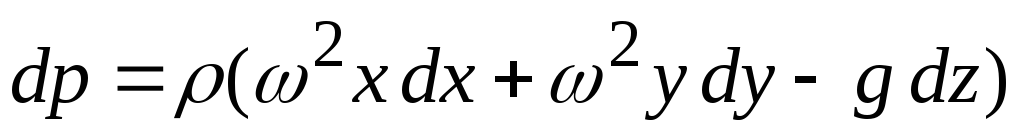
Для нахождения формы поверхностей равного давления произведем интегрирование при условии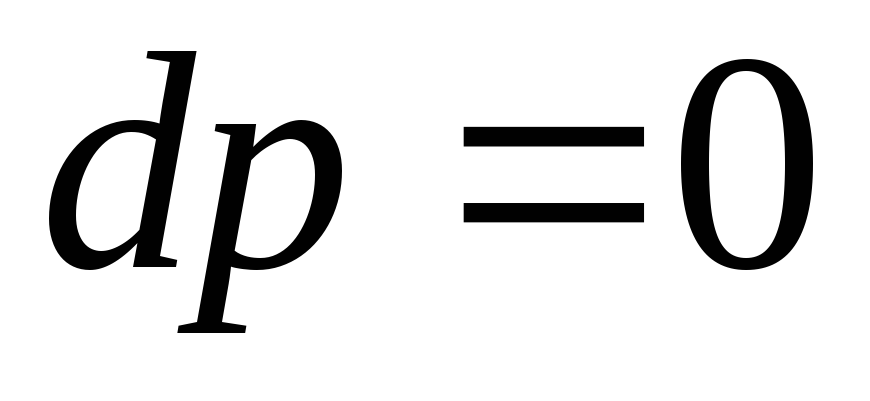 
.
или, поскольку 
,
, окончательно 
Из полученной формулы ясно, что поверхности равного давления представляют собой семейство конгруэнтных параболоидов вращения с вертикальной осью. Свободная поверхность – частный случай поверхности равного давления, во всех точках которой давление равно внешнему давлению 
. Координаты вершины параболоида 
, 
, 
, 
. 
.
Уравнение свободной поверхности 
Закон распределения давлений. Используем ранее полученное дифференциальное уравнение равновесия жидкости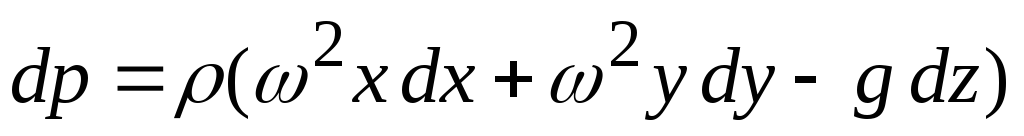 
. После интегрирования имеем:
. Из условий на вершине параболоида 
, 
, 
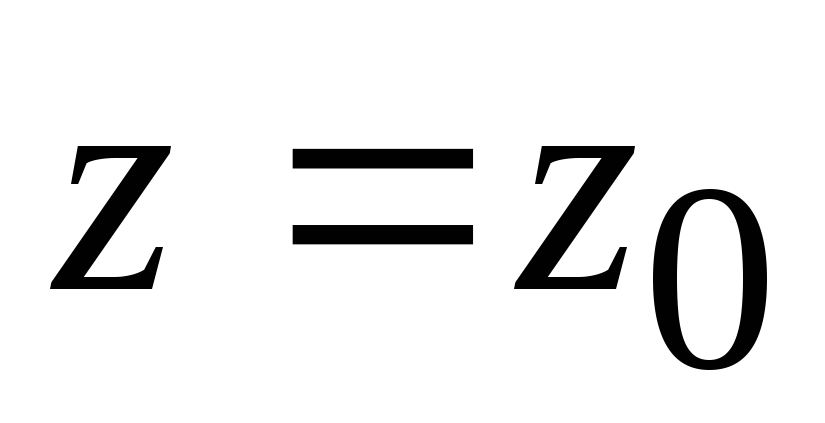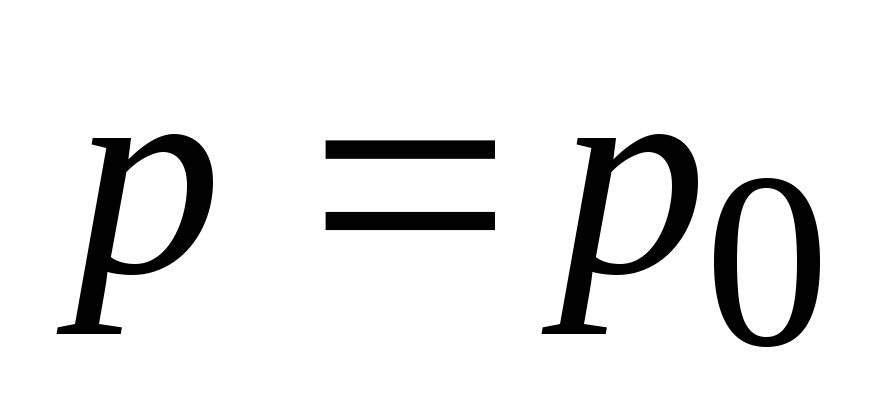найдем 
, после подстановки
Установим как распределяется давление по вертикали. Для этого подставим в полученное уравнение выражение из уравнения свободной поверхности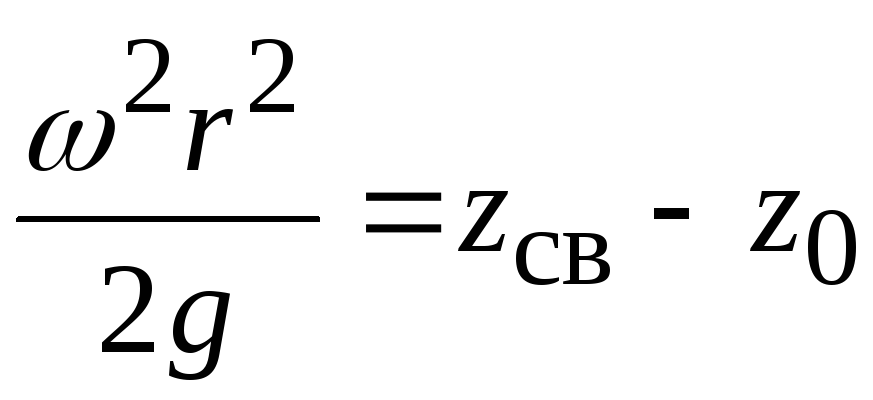 
.
, где
– глубина погружения точки под свободной поверхностью.
Таким образом, в жидкости, покоящейся в равномерно вращающемся сосуде, давление по вертикали распределяется по гидростатическому закону.
Соседние файлы в папке Lektsii
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Узнать стоимость
Под относительным покоем понимают неподвижное состояние жидкости относительно сосуда, который движется с постоянным ускорением. Например, в относительном покое может находиться жидкость в емкости, которая установлена на разгоняющейся транспортной машине (топливный бак автомобиля). В относительном покое будет также находиться жидкость в сосуде, вращающемся с постоянной скоростью.
Законы, действующие при относительном покое жидкости, принципиально не отличаются от ранее рассмотренных законов гидростатики. Но если в ранее рассмотренных случаях на жидкость действовала только одна массовая сила – сила тяжести, то при относительном покое появляется новая – сила инерции. Это приводит к изменению положения свободной поверхности жидкости и изменению давлений в различных ее точках.
Анализ относительного покоя удобно проводить для сил, действующих на условную частицу жидкости единичной массы (массой т = 1). При таком подходе сила всегда численно равна соответствующему ускорению. Например, на частицу единичной массы действует сила тяжести G = mg =1 g = g. Таким образом, математические зависимости существенно упрощаются.
Рассмотрим прямолинейное движение сосуда с постоянным ускорением (или замедлением) а. В этом случае на каждую частицу жидкости единичной массы действуют две силы: сила тяжести g сила инерции а (рисунок 2.9). Равнодействующая этих двух сил
(2.12)
определяет положение свободной поверхности жидкости, так как угол между этой поверхностью и силой всегда составляет 90°. Из геометрических соображений (см. рисунок 2.9) следует, что положение свободной поверхности может быть задано углом α, значение которого найдем из отношения
tga = а/g.
Для определения давления в произвольно выбранной точке на расстоянии l от свободной поверхности используется математическая зависимость
p = p0 + l ρ j. (2.13)
Она получена тем же методом, что и основное уравнение гидростатики, но учитывает действие не только сил тяжести, но и сил инерции.
Эта зависимость является более общей, чем основной закон гидростатики, который может быть получен из нее как частный случай. Действительно, при а= 0 из (2.12) следует j = g. Тогда c учетом l = h из (2.13) получим формулу (2.1), т.е. основное уравнение гидростатики.
Другим случаем относительного покоя жидкости является вращение сосуда с постоянной угловой скоростью ω (рисунок 2.10). При вращении на каждую частицу жидкости единичной массы, расположенную на радиусе r, также действуют две силы: сила тяжести g и сила инерции, вызванная центробежным ускорением, а = ω2 r. Равнодействующая этих двух сил
определяет положение свободной поверхности жидкости. Но в рассматриваемом случае центробежное ускорение является переменной величиной, так как зависит от радиуса расположения точки. Поэтому поверхность вращения принимает параболическую форму и описывается уравнением
,
где z0 – высота расположения точки свободной поверхности относительно дна сосуда;
h0 – высота жидкости на оси вращения.
Формула для определения давления р в любой точке жидкости может быть получена методом, использованным в подразделе 2.1. Тогда после математических преобразований найдем давление в точке, расположенной на радиусе r и высоте z относительно дна сосуда:
. (2.14)
На практике часто встречается другой частный случай – вращение сосуда с очень высокой скоростью. В этом случае центробежные силы существенно больше сил тяжести и жидкость отбрасывается центробежными силами к стенкам сосуда (рисунок 2.11), а ее свободная поверхность располагается на радиусе r0. Тогда некоторыми геометрическими величинами, входящими в формулу (2.12), можно пренебречь и формула для определения давления упрощается:
. (2.15)
Следует отметить, что формула (2.14) получена для сосуда, имеющего вертикальную ось вращения, а формула (2.15) применима для вращающихся сосудов с любым расположением оси в пространстве.
Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные корректировки и доработки. Узнайте стоимость своей работы.
Источник
: – ( ..) : : 1329 |
|
6., , . , , . . 1. , + (. 6.1, ) – (. 6, ).
6 . 6.1 , . . [1] = +(2 + )- () , = 0, gz = – (6.2) z – = tg ß = , (6.3) X g ß . 111 , , , .. = , = PS Z –X V 8 ) (6-4) (6.4) (0> /?) , z , .. , (. 6.2). , (6.4) = hc- – . (6.4) Z –X 8 7777) /////77//////?//// . 6.2 , . (< = 0), (6.1) = + 8? ■ , , , [2]. , [2]. 2. , + (. 6.3, ) – (. 6.3, ). = +8 V . . 1 + sm V 8 Z –X 8 , V (6.5) 113 . 6.3 (6.5) z + – 8 , , . ( = 90), (6.5) = Pq + Pg 1 + 8. ( = -90 ), . = Pq + Pg 1 gj z. (6.6) (6.7) (6.1)-(6.7) . (6.4) (6.5)-(6.7). . V, , (. 6.4): ={ +G+F = +Q, (6.8) { – ,
, = = P8hc, (6.9) . 6.4 114 hc – ( ); ; G – V, G = pgV; (6.10) F – , V , F = paV; (6.11) Q – , Q = G+F. (6.12) 3. , , – , . . P = Po+p(gz + wx)> (6.13) w – ; R X w = ‘R W = R (6.14) (6.15) – ; R – ; – . , = pQ, (6.13) gz = -wx (6.16) -=tgß= * g (6.17) ß – . pQ = 1 / W =8 z + -x , (6.18) V 8 W z ͗ X – 8 , . 115 (6.18) ( 0 > ) ( < /?) , z , .. , . 4. , . , . , , , w = G)V (öi – ), . , (. 6.6). (r,z)
z-z0 = () (6.19) + Zq ; , Z- . = . 6.6 2g ? – . 2 2 (!) 1″ = +–pg(z-z0), 2 (6.20) – z; 0- , z0. 116 , h ) P = Po+Pgh- (6-21) h ( – ) – ■ (6-22) (6.20) (. 6.6). ( ) hQ (. 6.6), hQ = – . 2 (6.23) , (. 6.7), = ^–2)- = 2 V 1 }2 2 (6.24) W R (!) . 6.7
117 , , , . . 6.8 , . Pz=PgVz, (6.25) Vz – , z, . 5. , . . , = (. 6.9, ). , , .. G)2r g. , (. 6.9, ). )7(7 -rQ2) = + (6.26) 0 – i% – .
CO . 6.9 119 (6.26) . . 6.9, . , (6.26) . 6.1. D = 1,2 L = 2,5 , ( 8 = 0,9 ) b = 1 , – ^ = 2 /2 (. 6.10). . g = 10 /. . ß, tgß= . 8 /, : La 2,5-2 Ah =–= -= 0,25. 2g 2- 2 7I-122 = pghCÄ(i)Ä = pg(b – Ah)-= 1 0,9 10(1 – 0,25)- = 7630 .
. 6.10 4 PB=PghCBB =pg(b + Ah) 1000-0,9-10(1+ 0,25) -1.212717. 6.2. , ( 5 = 0,9), / = 0,105. d = 0,7 , 120 (. 6.11) = 0,2 . , . . / = tgot. = 6. (6.3) (. 6.12) 2a/?cosoi d = ~g’ . 6.12 : 1 – ; 2 – ; 3 – .
. 6.12 . 6.11 : / = (/ – ) cosa = – tga V 2 J , , cosa. = — – tea 2 . ,1 cos2a 2 -g =
77777777777777777/ . 6.13 121 0 7 0,2-tg6 2 cos2 6 2 0,7 -9,81 = -4,52/2. – = -4,52 /. 6.3. , , ü = 36 / R = 300 . (. 6.13). . (6.15), . : >= =-= 0,333 / . R 300 (6.17) : ß = arctg 8 arctg 0 ,JJJ 9,81 -2, Di *4 , . 6.4. D{ = 300 L = 250 , D7 = 200 , = 900 / = 180 (. 6.14). , , . . , . . , 1, (. 6.15): ή . 6.14 4 3,14 2 4 4 V 2 0,25 0, 02 2 1,374-10 2 3. . 3,14-0, j 4 0,18: = 1,272-10″2 ~
124 VH < V, , 2 . (6.24), : = TigL2 3,14-9,81-0,252 = 25,4 “ 11,272 1 (2 – ^- (,32 – 0,22 ),25 (6.25): P = pgK=pgb =pg^-J:^ G)’ G)’ [ 8g 8g 900-3,14-25,4 64 (o,32 -0,22)2 = 71,2H. 6.1. L = 1 , = 0,5 = 0,7 h = 0,5 . , (. 6.16). 6.2. (- , (. 6.17). , h = 10 / = 20 ? 6.3. 6 = 1 , = 0,2g, , =1 h2 = 1,75 (. 6.18). , 1{ = 2 , l2 = 1 . 125
. 6.16 . 6.17 . 6.18 6.4. L = 2 , = 1 , b = 1 , = 6 /, h = 0,5 . , 0 = 0,2 105 (. 6.19). 6.5. = 4,0 /. , , L = 0,5 , b = 0,4 , = 0,2 , h = 10 (. 6.20). , , . 6.6. , = 1 /2, d = 0,2 , h = 0,4 (. 6.21). L . 6.19 . 6.20 .6.21 6.7. D = 2,4 L = 5,0 , ( 5 = 0,9) 6 = 2 , = 2 / (. 6.22). , ( . 6.22 ) V = 0,5 . g = 10 /. 126 6.8. (hc /), , = g (. 6.23). , : L = 2,88 , = 1,2 , h = 1,0 .
. 6.23 6.9. = 45 = 5,0 / , (. 6.24). , / = 0,5 . 1, 2 3, 4, , , b = 1 . 6.10. , h = 0,1 = 900 /, a = g (. 6.25). , , L = 1 , D = 0,5 . , / = 0,1 .
L . 6.24 . 6.25 127 6.11. – h = 0,48 (. 6.26). v = 36 / , . / = 3,0 , = 0,96 , -. 6.12. (hc /), , = 36 / R = 25 (. 6.27). , : = 1,8 , = 1,2 1,0 .
. 6.26 ////// 77777? . 6.27 6.13. =0,3 h = 0,2 . , , , , D = 100 (. 6.28). 6.14. , , . 6.29, . : D = 240 , d = 120 , = 50 . . , , , , . 6.15. , ) =) d = 0,60 , = 0,40 (. 6.30). 128 D D . 6.28 . 6.29 6.16. d , ) =10 “1, // = 0,86 (. 6.31). 6.17. d = 0,60 =1,5 , // = 1,0 , = 10 “1. (. 6.32). 6.18. , = 25 “1, (3 = 200 d = 150 D = 300 (. 6.33). . . d . 6.32 . 6.33 6.19. , D = 0,3 , d = 0,2 , b = 0,25 + b = 0,42 , = 450 /. , , = 50 (. 6.34). . 129 6.20. , , , ( = 900 /3) = 8000 / (. 6.35). , D = 120 , d = 30 . 0 = 0,5 . 6.21. D = 90 d = 20 (. 6.36). ), , h = 0,06 . , .
. 6.34 . 6.35 . 6.36 6.22. D = 180 = 0,6 ) = 200 “1. 7 – , 25 % (. 6.37). 6.23. . D = 200 = 1000 0 = 600 . , h = 100 (. 6.38). 6.24. , , d = 180 5 = 20 . 130 = 7000 / = 1000 / (. 6.39). D D
. 6.38 . 6.39 I 1 1 I I – 6.25. D = 380 6 = 210 , = 1000 /, V = 6 (. 6.40). , , . 6.26. , , / = 0,2. , (. 6.11). 6.27. , , , h{ = 1,0 h2 = 1,5 . , (. 6.18). 6.28. L = 2 , = 6 /2, h = 0,5 . , = 1,0 , 0 = 0,2-105 (. 6.19). . 6.40 132 6.29. , : L = 0,5 , b = 0,4 , = 0,2 , h = 10 (. 6.20), 7 . , . , , . 6.30. , = 160 , d = 0,2 , h = 0,4 . (. 6.21)? 6.31. D = 2,4 L = 5,0 , 6 = 1,8 , . , (. 6.22). 6.32. . = 0,5#, = 1,2 , L = 3,0 , h = 1,0 (. 6.23). 6.33. ( = 8000 /3). , , = 1000 /, D = 150 , d = 100 (. 6.41). 6.34. ( = 7000 /). , = 500 /, D = 1000 (. 6.42).
. 6.41 . 6.42 133 6.35. , , R = 100 60 /. , , : L = 3 , = 0,8 , = 1,8 . V = 3,0 3. , = 0,05 (. 6.43). 6.36. R = 50 / = 0,05. , (. 6.43). 6.37. = 250 d = 300 = 200 /. , d (. 6.44).
. 6.43 – 6 44 6.38. R = 100 , , // = 10. 6 = 10 . . 6.39. , , . , , , 1 . 134 .1 . 6.45 100 (. 6.41)? 6.40. . R (. 6.45). , , . h. 6.41. = 0,8 D = 0,4 ) =16 “1. , . 6.42. 頠 頠 = 0,75 D = 0,35 0 =0,3-105 . , , = 300 /. 6.43. < = 0,5 /” (. 6.46). , = 6 , = 4 , L = 10 , h = 0,8 , = 800 /3. 6.44. R = 200 20 /. , = 6 , L = 10 , = 4 (. 6.47). h = 0,8 , = 900 /3. . + L L R . 6.46 . 6.47 135 6.45. L = 2 , R = 0,5 8 = 10 . , 8 = 1 ? = 7000 / . 6.46. ( ) R = 50 = 25 (. 6.48). , ( = 800 /3) . 6.47. 8 = 10 , = 2 R = 0,5 , ) =142 “1 . , , – = 7000 / , 8 = 1 . 6.48. = 100 , 3/4 , = 10000 / (. 6.49). .
. 6.48 . 6.49 6.49. L = 2 R = 0,5 ay = 99 “1 . , . = 7000 /3. 136 6.50. R = 0,6 , , h = 1,2 : 1) = 12 “1; 2) , =12 “1 (. 6.50). 6.51. L = 2 R = 0,5 ( = 8000 / ) 5=10 . , = +1 . = 7000 /3. 6.52. , , = 36 / R = 300 (. 6.51). , .
. 6.51 6.53. D{ = 300 L = 250 , D2 = 200 , = 850 /3 = 200 = 20 “1 (. 6.14). , . 137 6.54. , 45 . , , v = 250 /. 6.55. D = 400 = 600 . , , , (. 6.52), h = 200 . 6.56. D = 300 = 400 , (. 6.53). , , , , ) = 20 “1. 6.57. (. 6.54) D = 200 =300 a = (),5g. , h = 100 , – . . D |
Источник