Жидкость в u образном сосуде
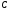
В огромном числе случаев при попытке построить модель какого-либо объекта либо невозможно прямо указать фундаментальные законы или вариационные принципы, которым он подчиняется, либо, с точки зрения наших сегодняшних знаний, вообще нет уверенности в существовании подобных законов, допускающих математическую формулировку. Одним из плодотворных подходов к такого рода объектам является использование аналогий с уже изученными явлениями.
Жидкость занимает часть
сосуда U-образной формы, представляющего собой изогнутую трубку
радиуса rо. Масса жидкости М0, ее плотность рo0. Стенки
сосуда идеально гладкие, поверхностным натяжением пренебрегается,
атмосферное давление Ро и ускорение свободного падения g постоянны.
В состоянии равновесия жидкость, очевидно, покоится, ее высота в обоих коленах сосуда одинакова. Если ее вывести из равновесия, то
начнется движение, характер которого установим с помощью ЗСЭ.
Потенциальную энергию системы вычислим через работу, которую необходимо совершить, чтобы переместить ее из состояния равновесия в положение, изображенное на рисунке.
где Р – вес той части жидкости в левом колене, уровень которой
превышает величину h2. Работа сил атмосферного давления равна нулю,
так как для разных колен соответствующие перемещения направлены
в разные стороны.
Неизвестные величины h1(t) и h2(t) связаны соотношением h1(t) + h2(t) = const > 0, выражающим постоянство полной длины столба жидкости в сосуде с постоянным сечением. Подставляя последнее равенство в выражение для Еп получаем после интегрирования
При вычислении кинетической энергии учтем постоянство сечения
трубки и несжимаемость жидкости. Это означает, что столб жидкости
движется как целое, и ее скорость v(t) одинакова во всех сечениях.
Примем за v(t) величину dh2(t)/dt и тогда
а из ЗСЭ следует
Так как dE/dt = 0, то, продифференцировав это выражение, получаем
что, с учетом такого же соотношения для величины h1(t), дает
уравнение
где h = (h2 – h1)/2 – отклонение уровня жидкости от положения
равновесия.
Т.е. в данной системе будут происходить незатухающие гармонические колебания.
48. Электрический колебательный контур.
В огромном числе случаев при попытке построить модель какого-либо объекта либо невозможно прямо указать фундаментальные законы или вариационные принципы, которым он подчиняется, либо, с точки зрения наших сегодняшних знаний, вообще нет уверенности в существовании подобных законов, допускающих математическую формулировку. Одним из плодотворных подходов к такого рода объектам является использование аналогий с уже изученными явлениями.
Это устройство представляет собой конденсатор, соединенный проводами с катушкой индуктивности. В момент t = 0 цепь замыкается, и заряд с обкладок
конденсатора начинает распространяться по цепи.
Сопротивление проводов будем считать равным нулю, емкость конденсатора равна С, индуктивность катушки L. Для изменяющейся со временем величины q(t), где q(t) – заряд на обкладках
конденсатора, необходимо получить соответствующее уравнение.
Ток i(t) и напряжение u(t) также являются функциями времени.
По физическому смыслу величины С в любой момент времени имеем равенство u(t) = q(t)С (емкость равна величине заряда, который необходимо поместить на обкладки конденсатора для увеличения разности потенциалов между ними на единицу).
Так как электрическое сопротивление в цепи отсутствует, то падения напряжения на проводах нет, и разность потенциалов u(t), существующая на конденсаторе, подается непосредственно на катушку. При переменном токе в катушке возникает электродвижущая сила самоиндукции, равная
 = -Ldi/dt. L- Коэффициент пропорциональности между изменением силы тока и ЭДС
= -Ldi/dt. L- Коэффициент пропорциональности между изменением силы тока и ЭДС
Закон Ома для цепи в отсутствие сопротивления выглядит следующим
образом: u(t) = – (t), или q(t)/C = –
(t), или q(t)/C = – (t) = Ldi/dt.
(t) = Ldi/dt.
Так как по определению i = -dq/dt (i- скорость изменения заряда
Э проходящего через сечение проводника), то из последнего соотношения
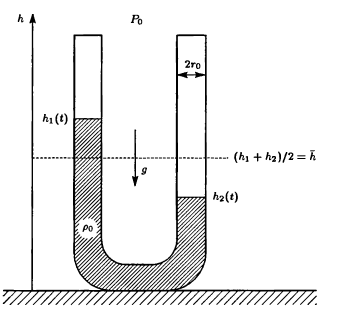
получаем уравнение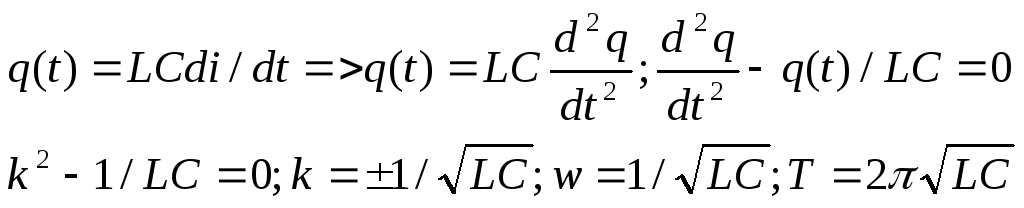
Т.е. в системе «емкость-индуктивность» колебания происходят также, как и в системе «шарик-пружина».
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник
U-образный манометр – это жидкостный манометр, состоящий из сообщающихся сосудов, в которых измеряемое давление определяют по одному или нескольким уровням жидкости/16/.
В U-образных стеклянных манометрах свободный конец трубки сообщается с атмосферой, а к другому концу подводится измеряемое давление. Простейшая схема измерения давления жидкостным стеклянным манометром показана на рис. 3.1.
Рис. 3.1. Схема функционирования стеклянного жидкостного манометра |
Атмосферное давление ратм воздействует на один конец U-образной трубки, частично заполненной рабочей жидкостью. Другой конец трубки с помощью различного рода подводящих устройств соединен с областью измеряемого давления рабс. При рабс > ратм жидкость, находящаяся в части подведенного измеряемого давления, будет вытесняться в часть, соединенную с атмосферой. В результате между уровнями жидкостей, находящимися в разных частях U-образной трубки, образуется столб жидкости, высота h которого определяется из выражения
h = (рабс – ратм)/((rж – rатм )g), (3.1)
где рабс- абсолютное измеряемое давление; rж – плотность рабочей жидкости; rатм – то же окружающей атмосферы; g – ускорение свободного падения, принимаемое в среднем равным 9,80665 м/с2, но имеющее зависимость от географической широты местности.
Высота столба рабочей жидкости h состоит из двух частей: высоты h1, представляющей понижение столба жидкости относительно начального – «нулевого» уровня, и высоты h2 – отражающей его повышение в другой части U-образной трубки, т. е. увеличение относительно начального положения – («нуля»).
Плотностью окружающей среды, т. е. воздуха из-за условия rж >> rатм можно пренебречь. Учитывая выражение (1.3), определяющее разность между абсолютным и атмосферным давлением как избыточное, зависимость (3.1) может быть представлена как
h = ризб/(rж g). (3.2)
Здесь ризб – измеряемое избыточное давление.
Из (3.2) измеряемое избыточное давление, определяемое с помощью стеклянного жидкостного манометра, может определяться как
ризб = hrж g. (3.3)
Для измерения давления разряженных газов используются жидкостные стеклянные манометры, схема которых представлена на рис. 3.2.
Рис. 3.2. Схема стеклянного жидкостного вакуумметра абсолютного давления |
В этих приборах к одному концу стеклянной U-образной трубки подводится вакуумметрическое давление, другой конец герметично запаян. Для этого случая выражение (3.1) в общем виде можно представить как
– h = (ратм – рабс)/(rж g). (3.4)
В торце запаянного конца давление равно нулю.
Если в запаянном конце будет находиться воздух, то вакуумметрическое избыточное давление может быть определено как
ратм – рабс = ризб – hrж g. (3.5)
В некоторых типах приборов воздух в запаянном конце «откачивается» и при заполнении рабочей жидкостью близко к «абсолютному нулю», т. е. прибор заполняется рабочей жидкостью под вакуумом и давление противодействия ратм = 0. Тогда выражение (3.5) может быть представлено в следующем виде:
рабс= hrж g. (3.6)
Конструкция, в которой запаянный конец перед заполнением рабочей жидкостью вакууммируется, может использоваться в качестве барометра. Отсчет значения барометрического давления производится по величине столба жидкости в запаянной части трубки.
Минус в уравнении (3.4) определяет вакуумметрическое давление. Высота столба жидкости h в этом случае определяет верхний предел диапазона измерения и является составляющей
h = h1 + h2. (3.7)
Здесь h1 и h2 – высота столбов жидкости, вытесненной под воздействием измеряемого давления от начальной отметки – нуля в двух трубках U-образного манометра.
Рис. 3.3. U-образный жидкостный стеклянный мановаку-умметр: 1 – U-образная стеклянная трубка; 2 – крепежные скобы; 3 – основание; 4 – шкальная пластина |
На рис.3.3 показан U-образный жидкостный стеклянный мановакуумметр. U-образная стеклянная трубка 1 с помощью скоб 2 крепится на металлическом или деревянном основании 3. На нем же между двумя трубками установлена шкальная пластина 4 с нанесенной линейной разметкой. Трубка заполняется рабочей жидкостью до нулевой отметки относительно шкальной пластины. Утолщения на концах стеклянной трубки предназначены для более плотного подсоединения резиновых шлангов.
При измерении избыточного давления к одному концу U-образной трубки подается среда измеряемого давления. Второй выход остается свободным и сообщается с атмосферой. Аналогичная ситуация происходит при измерении вакуумметрического давления. Симметричность линейной разметки на шкальной пластине обеспечивает применимость прибора для измерения избыточного и (или) вакуумметрического давления.
При измерении дифференциального (разностного) давления «плюсовый» и «минусовый» каналы подсоединяются к концам стеклянной U-образной трубки 1. Из-за симметричности линейной разметки практически отсутствуют различия в соответствии подведенного давления
на концах трубки.
U-образные жидкостные манометры с водой в качестве рабочей жидкости могут использоваться как напоромеры, тягонапоромеры и тягомеры для измерения давления воздуха, неагрессивных газов в диапазоне ±10 кПа. При давлении ±0,1 МПа рабочей жидкостью манометра может служить ртуть. Такие приборы применяются для измерения давления воды, неагрессивных жидкостей и газов.
Ниже приведены приблизительные оценки основных погрешностей, воздействующих, по данным С. Ф. Чистякова/2/, на точность показаний стеклянного жидкостного ма-нометра:
· погрешность градуировки шкалы составляет до 0,2-0,4 мм;
· смачиваемость стекла – капиллярные силы вносят неточность до 0,1-0,2 мм;
· отклонение прибора от строго вертикального положения может приводить к погрешности до 0,03 % на каждый градус.
Кроме этого, достаточно большую погрешность могут вносить: неравномерность сечения стеклянных трубок по их высоте, а при точных измерениях, как это следует из (3.3), варьирование плотности рабочей жидкости rж с изменением ее температуры, а также ускорение свободного падения g.
При использовании табличных данных погрешность определения плотности рабочей жидкости rж, по показателям разных авторов, не превышает 0,005 %. Следует обратить внимание на применение жидкостей, способных поглощать влагу или испаряться. Так, в большинстве случаев теоретическая и реальная плотности спиртов различаются, и табличные данные принимаются по некорректным начальным параметрам, что изначально приводит к появлению погрешности.
Некоторые производители к документации на жидкостный измеритель давления прилагают таблицу изменения плотности рабочей жидкости и поправок на вариацию этой плотности в зависимости от температуры, а также, например, для спиртов, таблицу зависимости плотности от его крепости.
Ускорение свободного падения g незначительно зависит от географической широты местности. его величина остается постоянной в рабочем регионе, не зависит от измеряемого давления, и поэтому вносимые этим параметром погрешности не превышают 10-3-10-4 %.
Визуальная оценка оператором уровня также может влиять на погрешность измерения. Разработаны различные методы снижения такой погрешности. Например, установка несложной оптической системы, позволяющей «накладывать» реальный и перевернутый мениски жидкости, обеспечивает значительное повышение точности отсчета уровня жидкости в жидкостном манометрическом приборе.
М. А. Гуляев и А. В. Ерюхин /24/ предложили в зависимости от применяемых способов следующие значения погрешностей отсчета уровня ртутного манометра:
· по миллиметровой шкале – ±1 мм;
· по зеркальной шкале – ±0,2-0,3 мм;
· с помощью нониусного устройства – ±0,05-0,1 мм;
· катетометром – ±0,2 мм;
· интерференционным методом – ±10-5 мм.
При отсчете измеряемого уровня необходимо учитывать свойства рабочих жидкостей, у которых угол смачиваемости x различен (рис. 3.4). Так, при использовании высокосмачиваемых жидкостей (вода, спирт) отсчет рекомендуется вести по вогнутой части мениска, а при применении несмачиваемых жидкостей (таких, как ртуть) – по выпуклой его части на оси трубки. Кроме этого, смачиваемость и текучесть жидкости предопределяют минимальный диаметр используемых трубок. При применении спирта в качестве рабочей жидкости рекомендуется минимальный внутренний диаметр стеклянных трубок 5 мм, ртути – 8 мм, воды – 15 мм.
Рис. 3.4. Вид менисков для различных жидкостей: а – смачивающей и б – несмачивающей |
При использовании ртути в качестве рабочей жидкости, особенно при точных измерениях, когда в чашечных манометрах применяются капилляры и сечения широкого сосуда и капилляра существенно отличаются, может наблюдаться эффект капиллярной депрессии. Сущность этого эффекта состоит в различии уровней несмачиваемой жидкости в сообщающихся капилляре и широком сосуде при воздействии одного и того же давления на поверхности жидкостей в этих объемах.
В промышленных условиях, как следует из приведенного выше материала, требуется тщательный контроль применяемых в жидкостных манометрах стеклянных трубок, так как их внутренний диаметр на практике может колебаться от 8 до 12 мм, что вносит существенные погрешности в результат измерения.
По данным разных специалистов/25/, без дополнительных оптических приспособлений погрешность показаний стеклянных жидкостных манометров принимается в лучшем случае равной ±1 мм. При использовании U-образных жидкостных манометрических приборов отсчет двух уровней (на каждой трубке) приводит к погрешности измерений ±2 мм при температуре окружающей среды 20 ± 5 °С. Верхние пределы измерений для стеклянных жидкостных манометров 100, 160, 250, 400, 600 и 1000 мм. Соответственно при одной и той же погрешности отсчета высоты столба жидкости класс точности жидкостного прибора колеблется от 2 до 0,2.
Для обеспечения корректности измерений обязательным является очистка внутренних поверхностей стеклянных трубок от пыли и грязи. С этой целью стеклянные жидкостные манометры промывают насыщенным раствором двухромовокислого калия (хромпика) в серной кислоте, затем – спиртом и водой.
Источник
Рассмотрим процессы колебаний в объектах различной природы. Покажем, что несмотря на разную сущность объектов, им соответствуют одни и те же математические модели.
1. Жидкость в u – образном сосуде.
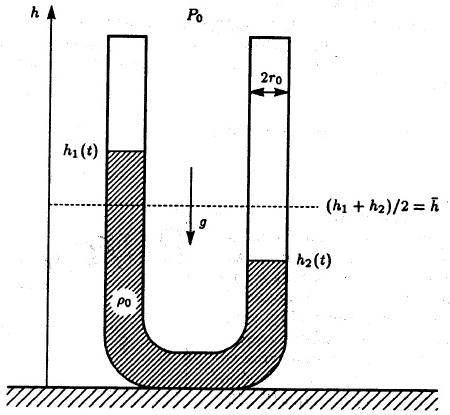
Жидкость занимает часть сосуда U – образной формы, представляющего собой изогнутую трубку радиуса . Масса жидкости , ее плотность . Стенки сосуда идеально гладкие, поверхностным натяжением пренебрегается, атмосферное давление и ускорение свободное падение постоянны.
В состоянии равновесия жидкость, очевидно, покоится, ее высота в обоих коленах сосуда одинакова. Если ее вывести из равновесия, то начнется движение, характер которого установим с помощью закона сохранения энергии, поскольку в силу сделанных предположений ее потери в системе отсутствуют.
Потенциальную энергии системы вычислим через работу, которую необходимо совершить, чтобы переместить ее из состояния равновесия (где ) в положение неравновесия.
Она равна
, , ,
где – вес той части жидкости в левом колене, уровень которой превышает величину . Работа сил атмосферного давления равна нулю, так как для разных колен соответствующие перемещения направлены в разные стороны.
Неизвестные величины и связаны очевидным соотношением , выражающим постоянство полной длины столба жидкости в сосуде с постоянным сечением. Поставляя последнее равенство в выражение для , получаем после интегрирования
.
При вычислении кинетической энергии учтем постоянство сечения трубки и несжимаемость жидкости. Это означает, что столб жидкости движется как целое, и ее скорость одинакова во всех сечениях. Примем за величину , и тогда
,
а из закона сохранения энергии следует
.
Так как , то продифференцировав это выражение, получаем
,
что с учетом такого же соотношения для величины , дает уравнение
,
где – отклонение уровня жидкости от положения равновесия. Оно с точностью до обозначений совпадает с уравнением для системы «шарик – пружина» (в данном случае аналогом шарика служит столб жидкости, а роль пружины играет тяготение). Последовательный отказ от идеализации объекта дает более полные его модели.
2. Колебательный электрический контур.
Это устройство представляет собой конденсатор, соединенный проводами с индуктивной катушкой. В момент цепь замыкается, и заряд с обкладок конденсатора начинает распространяется по цепи.
Сопротивление проводов будем считать равным нулю, емкость конденсатора равна , индуктивность катушки . Для изменяющейся со временем величины , где – заряд на обкладках конденсатора, необходимо получить соответствующее уравнение. Очевидно, что ток и напряжение также являются функциями времени. По физическому смыслу величины в любой момент времени имеет место равенство (емкость равна величине заряда, который необходимо поместить на обкладки конденсатора для увеличения разности потенциалов между ними на единицу).
Так как электрическое сопротивление в цепи отсутствует, то падение напряжения на проводах нет, и разность потенциалов , существующая на конденсаторе, подается непосредственно на катушку. При переменном токе в катушке возникает электродвижущая сила самоиндукции, равная . Закон Ома в цепи в отсутствие сопротивления выглядит следующим образом
,
или
.
Так как по определению (при изменении заряда на конденсаторе в цепи возникает ток), то из последнего соотношения получаем выражение
,
описывающее процесс колебаний величины (а, следовательно, и величин и ) в простейшем электрическом контуре. В системе «емкость – индуктивность» колебания происходят также, как и в системе «шарик – пружина».
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник
