Жидкость во вращающемся сосуде

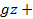
Возьмем открытый цилиндрический сосуд с жидкостью и сообщим ему постоянную угловую скорость w вращения вокруг вертикальной оси. Жидкость постепенно приобретет ту же угловую скорость, что и сосуд, а свободная поверхность ее видоизменится: в центральной части уровень жидкости понизится, у стенок – повысится, и вся свободная поверхность жидкости станет некоторой поверхностью вращения (рис. 2.11).

На жидкость в этом случае будут действовать две массовые силы, сила тяжести и центробежная сила, которые, будучи отнесенными к единице массы, соответственно равны g и w2r. Равнодействующая массовая сила j увеличивается с увеличением радиуса за счет второй составляющей, а угол наклона ее к горизонту уменьшается. Эта сила нормальна к свободной поверхности жидкости, поэтому угол наклона поверхности к горизонту возрастает с увеличением радиуса. Найдем уравнение положения свободной поверхности.

Рис. 2.11

Учитывая, что сила j нормальна к свободной поверхности, получим

отсюда
или после интегрирования
В точке пересечения свободной поверхности с осью вращения C = h, поэтому окончательно будем иметь
                                       (2.10)
т. е. свободная поверхность жидкости является параболоидом вращения.

Максимальную высоту подъема жидкости можно определить исходя из равенства объемов неподвижной жидкости и жидкости во время вращения.
На практике очень часто приходится иметь дело с вращением сосуда, заполненного жидкостью, вокруг горизонтальной оси. При этом угловая скорость w столь велика, что сила тяжести на порядок меньше центробежных сил, и ее действие можно не учитывать. Закон изменения давления в жидкости для этого случая получим из рассмотрения уравнения равновесия элементарного объема с площадью основания dS и высотой dr, взятой вдоль радиуса (рис. 2.12). На выделенный элемент жидкости действуют силы давления и центробежная сила.

Обозначив давление в центре площадки dS, расположенной на радиусе r, через p, а в центре другого основания объема (на радиусе r + dr) через p + dp, получим следующее уравнение равновесия выделенного объема в направлении радиуса

или

Рис. 2.12

После интегрирования

Постоянную C найдем из условия, что при r = r0 p = p0.
Следовательно

Подставив ее значение в предыдущее уравнение, получим связь между p и r в следующем виде:
(2.11)
Очевидно, что поверхностями уровня в данном случае будут цилиндрические поверхности с общей осью – осью вращения жидкости.

Часто бывает необходимо определить силу давления вращающейся вместе с сосудом жидкости на его стенку, нормальную к его оси вращения. Для этого определим силу давления, приходящуюся на элементарную кольцевую площадку радиусом r и шириной dr. Используя формулу (2.11), получим

а затем следует выполнить интегрирование в требуемых пределах.

При большой скорости вращения жидкости получается значительная суммарная сила давления на стенку. Это используется в некоторых фрикционных муфтах, где для сцепления двух валов требуется создание больших сил давления.

Источник

Рассмотрим случай, когда на жидкость, помимо объемных сил тяжести, действует еще другая система объемных сил, например, система центробежных сил инерции.

Возьмем круглоцилиндрический сосуд, наполненный жидкостью, причем будем считать, что этот сосуд вращается вокруг своей вертикальной оси равномерно, т. е. с постоянной угловой скоростью (рис. 2-14). Благодаря силам трения стенки вращающегося сосуда будут вначале увлекать за собой жидкость, а по истечении некоторого времени вся жидкость начнет вращаться вместе с сосудом с той же угловой скоростью Ω, находясь по отношению к стенкам сосуда в покое. Силы трения при этом внутри жидкости, а также между жидкостью, стенками сосуда и его дном, будут отсутствовать.

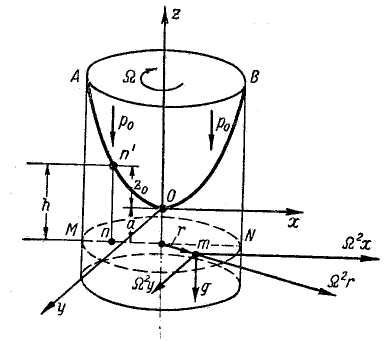
Жидкость во вращающемся сосуде

Рис. 2-14. Цилиндрический сосуд, вращающийся относительно вертикальной оси Oz

АОВ — свободная поверхность жидкости

Если оси координат, расположенные, как показано на чертеже, будем считать скрепленными с вращающимся сосудом, то по отношению к таким вращающимся осям координат жидкость также будет находиться в покое. Поэтому для исследования вращающейся жидкости при указанных подвижных осях координат могут быть применены известные уравнения Эйлера (2-14).

В эти уравнения входит объемная сила , действующая на единицу массы жидкости. В данном случае сила будет слагаться из двух сил: силы тяжести и центробежной силы.

С тем чтобы найти проекцию центробежной силы на оси координат, наметим внутри жидкости точку т и выделим у нее элементарную массу жидкости δM. Масса δM будет вращаться вокруг оси сосуда, двигаясь по окружности, имеющей радиус r и лежащей в плоскости, нормальной к оси сосуда. Центробежная сила, действующая на данную массу, будет

I’= , (2-62)

где υ – скорость движения массы δM по окружности радиуса r.

Центробежная сила, отнесенная к единице массы жидкости, сосредоточенной в точке т,

I = = Ω2r. (2-63)

Эта сила, так же как и сила I’, направлена по радиусу от оси сосуда наружу. Проекции силы I (отнесенной к единице м- ассы) на оси координат

Ix = Ω2rcos(r,x) = Ω2x

Iy = Ω2rcos(r,y) = Ω2y

Iz = 0 (2-64)

Проекции объемной силы тяжести, отнесенной к единице массы, выражаются зависимостью (2-28). Складывая объемные силы тяжести и объемные центробежные силы, отнесенные к единице массы, получаем

= 0 +Ω2x = Ω2x;

= 0 + Ω2y = Ω2y;

= – (2-65)

Подставляя (2-65) в (2-17), найдем

dpA = ρ(Ω2xdx + Ω2ydy – , (2-66)

что после интегрирования дает

dpA = ρ( + – ) + C = (x2 + y2) – ρ C. (2-67)

Постоянную интегрирования С устанавливаем, написав (2-67) применительно к точке, находящейся в начале координат, для которой x = y = z =0; p = p0. Как видно,

C = p0 (2-68)

причем (2-67) перепишется в виде:

pA = p0 + (x2 +y2) – γz (2-69)

Это последнее уравнение и выражает закон распределения давления в рассматриваемой жидкости. Пользуясь таким уравнением, можно найти поверхности равного давления.

Действительно, уравнение поверхности, во всех точках которой давление pA = pi= const, запишется в виде

(x2 +y2) – γz = pi – p0. (2-70)

Уравнение (2-70) выражает поверхность, являющуюся параболоидом вращения (с вертикальной осью).

Свободная поверхность жидкости, характеризуемая постоянным давлением pi = p0, представляет собой также параболоид вращения; уравнение ее будет:

(x2 +y2) – γz = 0. (2-71)

Если учесть, что x2 + y2 = r2, то, решив (2-71) относительно z, получим следующее уравнение, по которому легко построить параболу АОВ, дающую свободную поверхность:

z0 = r2 (2-72)

где z0- ордината кривой АОВ.

Распределение давления в горизонтальной плоскости MN, лежащей ниже начала координат на величину a, можно найти, пользуясь (2-69):

pA = p0 + (x2 +y2) +γa = p0 + ρ r2+ γa = p0 + γ( r2+ a). (2-73)

Учитывая (2-72), получаем

pA = p0 + γ(a + z0) = p0 + γh (2-74)

где h = a +z0 показано на рис. 2-14.

Таким образом, давление в жидкости, находящейся внутри равномерно вращающегося сосуда, выражается зависимостью того же вида, что и для случая тяжелой покоящейся жидкости [см. (2-39)]; под величиной h здесь надо понимать только заглубление рассматриваемой точки под криволинейной свободной поверхностью.

Источник

Сегодня я заварил себе чай и задумался

Сегодня утром я задумался, пока размешивал два кубика сахара в чашке с только что заваренным чаем. Задумался о форме жидкости, которую она принимает при вращении. Безусловно, все представляют себе что будет, если очень быстро начать размешивать сахар в чашке с чаем. Мне захотелось рассмотреть этот банальный и привычный процесс подробнее и попытаться рассказать Вам немного интересного из физики окружающих нас в быту явлений.

Идея эксперимента

Давайте представим, что мы имеем некоторую цилиндрическую тару, в которой находится некоторая жидкость. Вращаться жидкость можно заставить, как минимум, двумя очевидными способами: размешать её каким-нибудь предметом или начать вращать цилиндрическую тару, что, благодаря силам трения между жидкостью и поверхностью сосуда, приведет к вращению жидкости, увлекаемой содержащим её вращающимся сосудам.

Физическая модель

Остановимся на втором варианте. Итак, у нас есть вращающийся с постоянной циклической частотой сосуд, в котором при динамическом равновесии с постоянной циклической частотой вращается жидкость в том же направлении.

Вырежем из всей жидкости элементарный бесконечно малый объем около поверхности и рассмотрим какие силы на него действуют. В силу симметрии задачи, будем ориентироваться на цилиндрические координаты, что заметно упростит расчеты.

Качественный расчет формы поверхности

Запишем второй закон Ньютона для элементарного кусочка объема жидкости:

К примеру, после размешивания ложкой сахара в чашке только что заваренного чая, жидкость вращается вокруг оси симметрии, отсюда наш элементарный кусочек объема имеет центростремительное ускорение. Поэтому спроецируем наш закон Ньютона на ось, совпадающую с радиусом-вектором от элементарного объема до оси симметрии. Не будем учитывать вязкость и поверхностное натяжение. Сила, сообщающая центростремительное ускорение (в правой части нашего закона движения) возникнет из-за разности давлений столбов жидкости, что можно увидеть на увеличенной части первого рисунка.

Таким образом, у нас получится следующее выражение:
, где , а та самая сила определится как , где площадью эффективного сечения обозначена та площадь нашего элементарного объема, на которую действует разница давлений столбов жидкости .
Получаем силу

Масса нашего элемента объема определяется по знакомой всем формуле , а сам объем будет равен (элементарный объем в цилиндрических координатах).
В итоге, 2 закон Ньютона для нашей маленькой задачки расписывается в следующее выражение:

После небольших сокращений и преобразований получаем:

Теперь проинтегрируем обе части выражения, используя неопределенные интегралы:

Детальный расчет формы поверхности

Теперь мы получили вполне ясную зависимость для формы поверхности и с уверенностью можем сказать, что это параболоид. Но нам неизвестна постоянная величина . Давайте её определим для полного понимания физики процесса.

Так как объем жидкости не меняется (мы считаем, что не пролили ни капли, пока размешивали наш чай ツ), то запишем объемы до вращения и во время вращения с постоянной циклической частотой.

До вращения:
, где — это высота жидкости в цилиндрической поверхности в спокойном состоянии (вращения нет).

Во время вращения:

Данные объемы равны, поэтому:

Отсюда выражается ранее неизвестная постоянная:
И окончательное уравнение формы поверхности вращающейся жидкости имеет вид:
или преобразовав

Некоторые заметки

Хотелось бы обратить внимание на то, что форма поверхности зависит от частоты вращения, ускорения свободного падения, геометрических параметров сосуда, первоначального объема жидкости, но не зависит от плотности жидкости. Это выражение мне показалось довольно интересным, так как с его помощью можно легко смоделировать примерное расположение жидкости внутри вращающегося вокруг своей оси симметрии цилиндрического сосуда. Для этого можно воспользоваться MathCAD’ом и построить несколько графиков.

Графическое представление результатов расчета

Возьмем вполне реальные параметры системы, соизмеримые с размерами чашки или стакана.
Радиус цилиндрической поверхности:
Высота жидкости в цилиндрической поверхности без вращения:
Ускорение свободного падения:
Циклическая частота вращения цилиндрической поверхности:
(Все значения этих величин заданы в системе Си)

Далее перепишем нашу функцию для её отображения в MathCAD.
Для 2D отображения сечения:

Для 3D отображения поверхности:

В качестве изменяющегося параметра будем менять циклическую частоту вращения . Результаты можно наблюдать на рисунках ниже:

При циклической частоте

Выводы

Видно, что если циклическая частота превысит значение , то мы увидим дно вращающегося цилиндрического сосуда, и, начиная с этой частоты, жидкость будет плавно «переходить» на стенки сосуда, всё сильнее оголяя дно. Очевидно, что при очень больших частотах вся жидкость растечется по стенкам сосуда. Теперь мы знаем все параметры такой жидкости. Зная её уравнение, не составит большого труда рассчитать толщину слоя жидкости на стенке сосуда на определенной высоте при определенной частоте.

upd. Отдельно хотелось бы подчеркнуть те противоречащие друг другу допущения, которые были приняты при рассмотрении задачи:
1. Считалось что, жидкость вращается благодаря вращению сосуда, который её содержит. Это может быть только при учете внутреннего трения, вязкости и поверхностного натяжения.
2. Но при выводе формы поверхности эти явления не учитываются для того, чтобы упростить решение и показать только качественный результаты моделирования. Т.е. решение немного противоречит описываемой изначально модели. Учет всех явлений, включая нелинейность процесса при высоких частотах, настолько бы усложнил задачу, что её вряд ли можно было бы решить аналитически и показать примерную и понятную модель для человека, который не связан с математикой/физикой.
3. Цель состоялась в том, чтобы показать лишь очень приближенное и самое простое решение, включающее в себя ряд допущений.

Источник

Содержание:

Равновесие жидкости в сосуде, равномерно вращающемся относительно вертикальной оси.

Равновесие жидкости в сосуде, равномерно вращающемся относительно вертикальной оси

Равновесие жидкости в сосуде, равномерно вращающемся относительно вертикальной оси. В состоянии равновесия в движущемся сосуде жидкость движется вместе со всем контейнером. То есть, жидкость находится в относительном состоянии покоя. Рассмотрим цилиндрический контейнер радиусом H (рис. 2.9), заполненный до определенного уровня жидкостью плотностью p и вращающийся с постоянной угловой скоростью относительно вертикальной оси.

Через некоторое время после начала вращения сосуда жидкость под действием трения вращается с той же скоростью, что и сосуд. Равновесие жидкости устанавливается для сосуда, другими словами, для неинерциальных систем координат x, y, r, которые вращаются вместе с сосудом. При написании уравнений равновесия в неинерциальных системах необходимо ввести силу подвижной инерции в число рабочих forces.

В абсолютно покоящейся жидкости (сосуд неподвижен) действующей массовой силой (в поле сил тяжести) является только сила тяжести.
Людмила Фирмаль

В рассматриваемом случае такая сила направлена вдоль радиуса и равна & M (центробежная сила равна n2g элементарной массы AM, которая вращается на расстоянии r от вертикали axis. In помимо центробежной силы, гравитация DM ^действует на любую частицу AM-это: за счет силы тяжести ^ = ° ;=°; ПГХ = —§; От портативной инерции п *. =<sup class=»reg»>®</sup>ГХ Риш-0)2 в> пр%= 0、 Где*и y-горизонтальные координаты произвольно выбранной точки А в жидкости. Рассмотрим 2 вопроса здесь. 39.

Форма поверхности одинакового давления. Используйте уравнение поверхности равного давления (2.10)’ Rhyh + ру ю + Rghyg-0 Когда вы назначаете ему выражения Px, Py и Pr, вы находите co2 x yx + co2 yy-diig-0. После интеграции、 гг-(* 2 + У2) §Р= С Или Х2 + У2-Г2.、 СО2-Р2 / 2 §р= с(2.23） Как видно из (2.23), поверхность равного давления в этом случае представляет собой семейство совпадающих 1-вращающихся параболоидов с вертикальной осью. Различные значения константы C соответствуют различным параболам одинакового давления.

Свободная поверхность это также поверхность, на которой давление во всех точках равно давлению, равному внешнему давлению p0. Найти значение любой константы c параболоида свободной поверхности. Х-0; У = 0; РСВ = Р0.Если подставить эти координаты в Формулу (2.23), то: Ц0 = § 0. Уравнения свободной поверхности * С ш-Р0 = ^ (*2 +! 2. ） 2-й. Или Огнестрел-20 = СО2 Г2 / 2Д, (2.24） Частицы жидкости, находящиеся в относительном стационарном состоянии во вращающемся сосуде на расстоянии радиуса r от оси вращения, имеют линейную скорость u-(π.

Высота, на которой точка свободной поверхности выше вершины параболоида(например、 Б = РК-Р0 = СО2 Р2 /2§= С2 / 2С (2.25） 1 матч-фигура, которая будет объединена при наложении. 40. 20 ордината вершины параболоида свободной поверхности при заданной угловой скорости зависит от количества жидкости в сосуде. Если перед вращением сосуда уровень жидкости был установлен на горизонтальную и высоту H, то объем жидкости был равен 2N2H.

Законы относительного равновесия жидкости находят широкое применение в промышленности, а именно, в измерительной технике (жидкостные тахометры), в металлургии (центробежное литье) и других областях техники.
Людмила Фирмаль

При вращении сосуда свободная поверхность становится параболой, форма объема жидкости изменяется, а величина при p = const{остается неизменной： | (Р0 +(r212d О2 ） О После интеграции、 Ч ■= рН + П2 К2 / 4Д Или Р0 = я-п * д * / 4#. Предполагая, что 20 = 0, мы знаем угловую скорость a, когда свободная поверхность жидкости касается дна контейнера. w = 2 Уды / я. Закон распределения давления. Используя дифференциальное уравнение жидкостных равновесий (2.5) и подставляя в него проекцию распределения плотности массовых сил, он выглядит следующим образом: гг = pY2(xc1x + ыыы) Сделай сам.

После интегрирования уравнения(2.26)、 / ? п(w2g72-ДГ)+ КБ(2.27） Если подставить координаты r = 0, r-r0 и давление p = p0 в уравнение (2.27), то получим Cp. С1! = Р0-Р (н0)= Р0 + rd0 Подставляя найденные значения C1 в(2.27), получаем 2r2 / 2d = H ’позволяет переписать любую точку в виде (2.28). Здесь k-глубина погружения точки под свободную поверхность, то есть вертикальное расстояние от свободной параболы до точки задачи. Поэтому в жидкости, которая неподвижна в равномерно вращающемся сосуде, вертикальное давление распределяется по закону гидростатического давления.

Смотрите также:

Задачи по гидравлике

Возможно эти страницы вам будут полезны:

Равновесие однородной несжимаемой жидкости относительно земли.
Геометрическая интерпретация основного уравнения гидростатики.
Силы давления покоящейся жидкости на горизонтальные и наклонные плоские площадки (стенки).
Силы давления покоящейся жидкости на цилиндрические стенки.

Источник

В зависимости от характера действующих массовых сил поверхность равного давления в жидкости, как и свободная поверхность, может принимать
различную форму. Ниже рассматриваются некоторые случаи равновесия жидкости в движущихся сосудах.

1. Жидкость находится в сосуде, который движется в горизонтальном направлении с постоянным ускорением ±а (знак плюс соответствует ускорению сосуда, знак минус – замедлению ) (см. рисунок).

Жидкость во вращающемся сосуде

В данном случае жидкость подвержена воздействию не только поверхностных сил, но также массовых сил тяжести и инерции.
Поверхность равного давления является наклонной плоскостью. Давление в любой точке жидкости определяется по формуле

p = p0 + ρ·(g·z ± a·x),

Для свободной поверхности жидкости, когда р=p0, уравнение принимает вид:

g·z = ± a·x
или
z/x = tg α = ± a/g,

где α – угол наклона свободной поверхности жидкости к горизонту.

Последнее приведенное выше выражение позволяет определять (при условии, чтобы жидкость не переливалась через задний борт сосуда длиной l)
высоту борта h при заданном значении а или предельное ускорение а при заданном значении h.

Если сосуд движется равномерно (а = 0), уравнение приводим к виду:

p = p0 + ρ·g·z = p0·γ

В этом случае поверхность равного давления представляет горизонтальную плоскость.

2. Жидкость находится в открытом цилиндрическом сосуде, который вращается вокруг вертикальной оси с постоянной угловой скоростью ω.

Жидкость во вращающемся сосуде

В данном случае жидкость подвержена воздействию не только поверхностных сил, но также массовых сил тяжести и центробежной.

Поверхность равного давления представляет параболоид вращения. Распределение давления в жидкости по глубине определяется выражением:

p = p0 + γ·((ω2·r2)/(2·g) – z)

Для любой точки свободной поверхности жидкости, когда p = p0, уравнение принимает вид:

z = (ω2·r2)/(2·g) = u2/(2·g),

где окружная скорость u = ω·r (r — радиус вращения точки).

Высота параболоида вращения:

h = ω2·r20/(2·g),

где r0 – радиус цилиндрического сосуда.

Сила давления жидкости на дно сосуда:

P = γ·π·r20·h0 = γ·π·r20·(h1 + h/2),

где h0 – начальная глубина жидкости в сосуде до момента его вращения.

Давление на боковую стенку сосуда изменяется по линейному закону. Эпюра давления представляет прямоугольный треугольник ACD с высотой h1 + h и основанием γ·(h1 + h).

3. Жидкость находится в цилиндрическом сосуде, который вращается вокруг горизонтальной оси с постоянной угловой скоростью ω.

В данном случае жидкость также подвержена воздействию массовых сил тяжести и центробежной.

Поверхности равного давления представляют концентрически расположенные боковые поверхности цилиндров, оси которых горизонтальны и смещены относительно оси оу на величину эксцентриситета e = g/ω2 (см. рисунок а).

Жидкость во вращающемся сосуде

При большом числе оборотов сосуда влияние силы тяжести по сравнению с влиянием центробежной силы становится незначительным, и, следовательно, величиной эксцентриситета е можно пренебречь. Тогда поверхности равного давления становятся концентрическими цилиндрами, оси которых совпадают с осью сосуда (см. рисунок б).

Распределение давления по глубине жидкости определяется выражением:

p = p0 + γ·ω2·(r2 – r20)/(2·g)

где p и p0 – соответственно давления в точках цилиндрических поверхностей с радиусами r и r0.

Данное уравнение справедливо и тогда, когда сосуд радиусом r лишь частично заполнен жидкостью. Свободная поверхность жидкости в этом случае также будет цилиндрической с радиусом r0 и давлением во всех ее точках р0.

Как видно из последнего уравнения, закон распределения давления по радиусу является параболическим. Эпюра давления представленная на рисунке в.
Такие приближенные решения могут применяться при любом положении оси вращения сосуда, однако при условии большого числа его оборотов.

Вильнер Я.М. Справочное пособие по гидравлике, гидромашинам и гидроприводам.

Источник