Жидкости в крае сосуда
Среди процессов, которые можно объяснить с помощью поверхностного натяжения и смачивания жидкостей, стоит особо выделить капиллярные явления. Физика – это загадочная и необыкновенная наука, без которой жизнь на Земле была бы невозможна. Давайте рассмотрим наиболее яркий пример этой важной дисциплины.
В жизненной практике такие интересные с точки зрения физики процессы, как капиллярные явления, встречаются весьма часто. Все дело в том, что в повседневной жизни нас окружает много тел, которые легко впитывают в себя жидкость. Причина этому – их пористая структура и элементарные законы физики, а результат – капиллярные явления.
Узкие трубки
Капилляр – это очень узкая трубка, в которой жидкость ведет себя особым образом. Примеров таких сосудов много в природе – капилляры кровеносной системы, пористых тел, почвы, растений и т. д.

Капиллярным явлением называется подъем или опускание жидкостей по узким трубкам. Такие процессы наблюдаются в естественных каналах человека, растений и других тел, а также в специальных узких сосудах из стекла. На картинке видно, что в сообщающихся трубках разной толщины установился разный уровень воды. Отмечено, что чем тоньше сосуд, тем выше уровень воды.
Эти явления лежат в основе впитывающих свойств полотенца, питания растений, движения чернил по стержню и многих других процессов.
Капиллярные явления в природе
Описанный выше процесс чрезвычайно важен для поддержания жизнедеятельности растений. Почва довольно рыхлая, между ее частицами существуют промежутки, которые представляют собой капиллярную сеть. По этим каналам поднимается вода, питая корневую систему растений влагой и всеми необходимыми веществами.
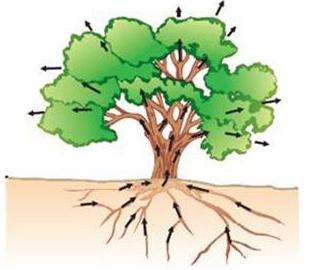
По этим же капиллярам жидкость активно испаряется, поэтому необходимо производить вспахивание земли, которое разрушит каналы и удержит питательные вещества. И наоборот, прижатая земля быстрее испарит влагу. Этим обусловлена важность перепашки земли для удержания подпочвенной жидкости.
В растениях капиллярная система обеспечивает подъем влаги от мелких корешков до самых верхних частей, а через листья она испаряется во внешнюю среду.
Поверхностное натяжение и смачивание
В основе вопроса о поведении жидкости в сосудах лежат такие физические процессы, как поверхностное натяжение и смачивание. Капиллярные явления, обусловленные ими, изучаются в комплексе.

Под действием силы поверхностного натяжения смачивающая жидкость в капиллярах находится выше уровня, на котором она должна находиться согласно закону сообщающихся сосудов. И наоборот, несмачивающая субстанция располагается ниже этого уровня.
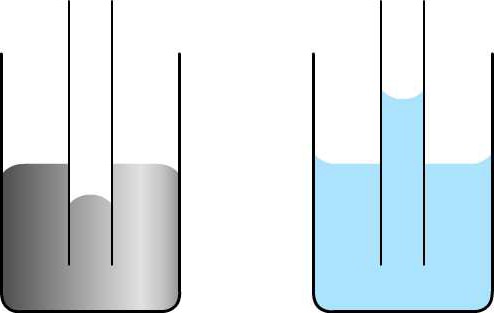
Так, вода в стеклянной трубке (смачивающая жидкость) поднимается на тем большую высоту, чем тоньше сосуд. Напротив, ртуть в стеклянной пробирке (несмачивающая жидкость) опускается тем ниже, чем тоньше эта емкость. Кроме того, как указано на картинке, смачивающая жидкость образует вогнутую форму мениска, а несмачивающая – выпуклую.
Смачивание
Это явление, которое происходит на границе, где жидкость соприкасается с твердым телом (другой жидкостью, газами). Оно возникает по причине особого взаимодействия молекул на границе их контакта.
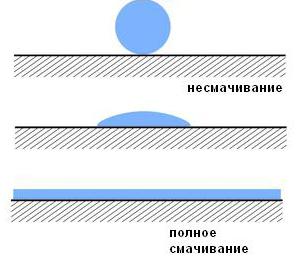
Полное смачивание означает, что капля растекается по поверхности твердого тела, а несмачивание преобразует ее в сферу. На практике чаще всего встречается та или иная степень смачивания, нежели крайние варианты.
Сила поверхностного натяжения
Поверхность капли имеет шарообразную форму и причина этому закон, действующий на жидкости, – поверхностное натяжение.

Капиллярные явления связаны с тем, что вогнутая сторона жидкости в трубке стремится выпрямиться до плоского состояния благодаря силам поверхностного натяжения. Это сопровождается тем, что наружные частицы увлекают за собой вверх тела, находящиеся под ними, и субстанция поднимается вверх по трубке. Однако жидкость в капилляре не может принимать плоскую форму поверхности, и этот процесс подъема продолжается до определенного момента равновесия. Чтобы рассчитать высоту, на которую поднимется (опустится) столб воды, нужно воспользоваться формулами, которые будут представлены ниже.
Расчет высоты подъема столба воды
Момент остановки подъема воды в узкой трубке наступает, когда сила тяжести Ртяж субстанции уравновесит силу поверхностного натяжения F. Этот момент определяет высоту подъема жидкости. Капиллярные явления обусловлены двумя разнонаправленными силами:
- сила тяжести Ртяж заставляет жидкость опускаться вниз;
- сила поверхностного натяжения F двигает воду вверх.
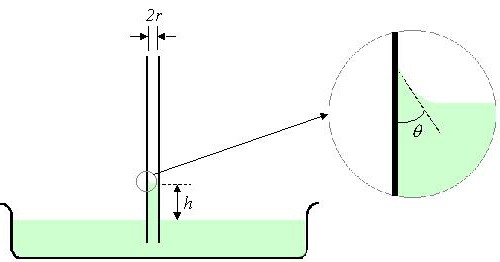
Сила поверхностного натяжения, действующая по окружности, где жидкость соприкасается со стенками трубки, равна:
F = σ2πr,
где r – радиус трубки.
Сила тяжести, действующая на жидкость в трубке равна:
Ртяж = ρπr2hg,
где ρ – плотность жидкости; h – высота столба жидкости в трубке;
Итак, субстанция прекратит подниматься при условии, что Ртяж = F, а это значит, что
ρπr2hg = σ2πr,
отсюда высота жидкости в трубке равна:
h=2σ/pqr.
Точно так же для несмачивающей жидкости:
h – это высота опускания субстанции в трубке. Как видно из формул, высота, на которую поднимется вода в узком сосуде (опустится) обратно пропорционально радиусу емкости и плотности жидкости. Это касается смачивающей жидкости и несмачивающей. При других условиях нужно делать поправку по форме мениска, что будет представлено в следующей главе.
Лапласовское давление
Как уже отмечалось, жидкость в узких трубках ведет себя так, что создается впечатление нарушения закона сообщающихся сосудов. Этот факт всегда сопровождает капиллярные явления. Физика объясняет это с помощью лапласовского давления, которое при смачивающей жидкости направлено вверх. Опуская очень узкую трубку в воду, наблюдаем, как жидкость втягивается на определенный уровень h. По закону сообщающихся сосудов, она должна была уравновеситься с внешним уровнем воды.
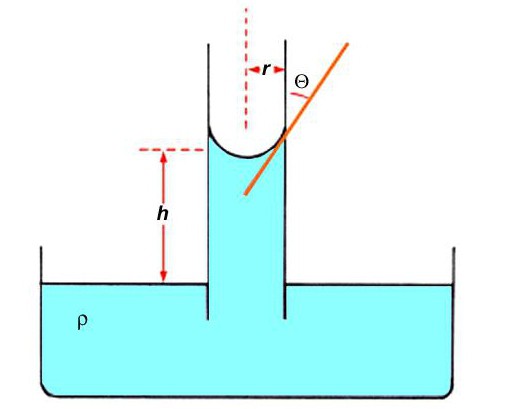
Это несоответствие объясняется направлением лапласовского давления pл:
pл=2σ/R,
В данном случае оно направлено вверх. Вода втягивается в трубку до уровня, где приходит уравновешивание с гидростатическим давлением pг столба воды:
pг=pqh,
а если pл=pг, то можно приравнять и две части уравнения:
2σ/R= pqh.
Теперь высоту h легко вывести в виде формулы:
h=2σ/pqR.
Когда смачивание полное, тогда мениск, который образует вогнутая поверхность воды, имеет форму полусферы, где Ɵ=0. В таком случае радиус сферы R будет равен внутреннему радиусу капилляра r. Отсюда получаем:
h=2σ/pqr.
А в случае неполного смачивания, когда Ɵ≠0, радиус сферы можно вычислить по формуле:
R=r/cosƟ.
Тогда искомая высота, имеющая поправку на угол, будет равна:
h=(2σ/pqr)cosƟ.
Из представленных уравнений видно, что высота h обратно пропорциональна внутреннему радиусу трубки r. Наибольшей высоты вода достигает в сосудах, имеющих диаметр человеческого волоса, которые и называются капиллярами. Как известно, смачивающая жидкость втягивается вверх, а несмачивающая – выталкивается вниз.
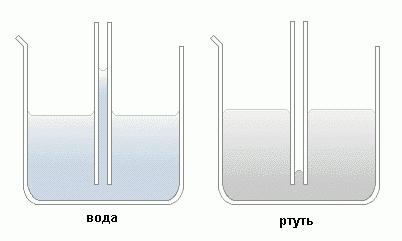
Можно провести эксперимент, взяв сообщающиеся сосуды, где один из них широкий, а другой – очень узкий. Налив туда воду, можно отметить разный уровень жидкости, причем в варианте со смачивающей субстанцией уровень в узкой трубке выше, а с несмачивающей – ниже.
Важность капиллярных явлений
Без капиллярных явлений существование живых организмов просто невозможно. Именно по мельчайшим сосудам человеческое тело получает кислород и питательные вещества. Корни растений – это сеть капилляров, которая вытягивает влагу из земли, донося ее до самых верхних листьев.
Простая бытовая уборка невозможна без капиллярных явлений, ведь по этому принципу ткань впитывает воду. Полотенце, чернила, фитиль в масляной лампе и множество устройств работает на этой основе. Капиллярные явления в технике играют важную роль при сушке пористых тел и других процессах.
Порой эти же явления дают нежелательные последствия, например, поры кирпича впитывают влагу. Чтобы избежать отсыревания зданий под воздействием грунтовых вод, нужно защитить фундамент с помощью гидроизолирующих материалов – битума, рубероида или толя.
Промокание одежды во время дождя, к примеру, брюк до самых колен от ходьбы по лужам также обязано капиллярным явлениям. Вокруг нас множество примеров этого природного феномена.
Эксперимент с цветами
Примеры капиллярных явлений можно найти в природе, особенно если говорить о растениях. Их стволы имеют внутри множество мелких сосудов. Можно провести эксперимент с окрашиванием цветка в какой-либо яркий цвет в результате капиллярных явлений.

Нужно взять ярко окрашенную воду и белый цветок (или лист пекинской капусты, стебель сельдерея) и поставить в стакан с этой жидкостью. Через какое-то время на листьях пекинской капусты можно наблюдать, как краска продвигается вверх. Цвет растения постепенно изменится соответственно краске, в которую он помещен. Это обусловлено движением субстанции вверх по стеблям согласно тем законам, которые были рассмотрены нами в этой статье.
Источник
Авторы: А. М. Емельяненко, Н. В. Чураев
КАПИЛЛЯ́РНЫЕ ЯВЛЕ́НИЯ, совокупность явлений, обусловленных поверхностным натяжением на границе раздела несмешивающихся сред (в системах жидкость – жидкость, жидкость – газ или пар) при наличии искривления поверхности. Частный случай поверхностных явлений.

Рис. 1.
При отсутствии силы тяжести жидкость ограниченной массы под воздействием поверхностного натяжения стремится занять объём с миним. поверхностью, т. е. принимает форму шара. В условиях действия силы тяжести не слишком вязкая жидкость достаточной массы принимает форму сосуда, в который налита, и её свободная поверхность при относительно большой площади (вдали от стенок сосуда) становится плоской, т. к. роль поверхностного натяжения менее существенна, чем силы тяжести. При взаимодействии с поверхностью др. жидкости или твёрдого тела (напр., со стенками сосуда) поверхность рассматриваемой жидкости искривляется в зависимости от наличия или отсутствия смачивания. Если имеет место смачивание, т. е. молекулы жидкости 1 (рис. 1) сильнее взаимодействуют с молекулами поверхности 3, чем с молекулами др. жидкости (или газа) 2, то под воздействием разности сил межмолекулярного взаимодействия жидкость 1 поднимается по стенке сосуда – участок жидкости, примыкающий к стенке, искривляется. Давление, вызываемое подъёмом жидкости, уравновешивается капиллярным давлением $Delta p$ – разностью давлений над и под искривлённой поверхностью раздела. Величина капиллярного давления зависит от среднего радиуса $r$ кривизны поверхности и определяется формулой Лапласа: $Delta p=2 sigma/r$, где $sigma$ – поверхностное натяжение. Если граница раздела фаз плоская ($r= infty$), то в условиях механич. равновесия системы давления с обеих сторон границы раздела равны и $Delta p=0$. В случае вогнутой поверхности жидкости ($r lt 0$) давление в жидкости ниже, чем давление в граничащей с ней фазе и $Delta p lt 0$; для выпуклой поверхности ($r>0$) $Delta p>0$.
Если стенки сосуда приблизить друг к другу, зоны искривления поверхности жидкости образуют мениск – полностью искривлённую поверхность. Образовавшаяся система называется капилляром; в нём в условиях смачивания давление под мениском понижено и жидкость в капилляре поднимается (над уровнем свободной поверхности жидкости в сосуде); вес столба жидкости высотой $h$ уравновешивает капиллярное давление $Delta p$. Несмачивающая жидкость в капилляре образует выпуклый мениск, давление над которым выше, и жидкость в нём опускается ниже уровня свободной поверхности вне капилляра. Высота поднятия (опускания) жидкости в капилляре относительно свободной поверхности (где $r= infty$ и $Delta p=0$) определяется соотношением: $h=2 sigma cos theta/ Delta rho gr$, где $theta$ – краевой угол (угол между касательной к поверхности мениска и стенкой капилляра), $Delta rho$ – разность плотностей жидкости 1 в капилляре и внешней среды 2, $g$ – ускорение свободного падения.
Искривление поверхности влияет на условия равновесия между жидкостью и её насыщенным паром: согласно Кельвина уравнению, давление паров над каплей жидкости повышается с уменьшением её радиуса, что объясняет, напр., рост больших капель в облаках за счёт малых.

Рис. 2.
К характерным К. я. относятся капиллярное впитывание, появление и распространение капиллярных волн, капиллярное передвижение жидкости, капиллярная конденсация, процессы испарения и растворения при наличии искривлённой поверхности. Капиллярное впитывание характеризуется скоростью, зависящей от капиллярного давления и вязкости жидкости. Оно играет существенную роль в водоснабжении растений, движении воды в почвах и др. процессах, связанных с движением жидкостей в пористых средах. Капиллярная пропитка – один из распространённых процессов химич. технологии. В системах с непараллельными стенками (или капиллярах конич. сечения) кривизна менисков зависит от расположения в них граничных поверхностей жидкости, и капля смачивающей жидкости в них начинает двигаться к мениску с меньшим радиусом (рис. 2), т. е. в ту сторону, где давление ниже. Причиной капиллярного передвижения жидкости может служить и разница сил поверхностного натяжения в менисках, напр. при существовании градиента темп-ры или при адсорбции поверхностно-активных веществ, снижающих поверхностное натяжение.
Капиллярной конденсацией называют процесс конденсации пара в капиллярах и микротрещинах пористых тел, а также в промежутках между сближенными твёрдыми частицами или телами. Необходимое условие капиллярной конденсации – наличие смачивания поверхности тел (частиц) конденсирующейся жидкостью. Процессу капиллярной конденсации предшествует адсорбция молекул пара поверхностью тел и образование менисков жидкости. В условиях смачивания форма менисков вогнутая и давление $p$ насыщенного пара над ними ниже, чем давление насыщенного пара $p_0$ при тех же условиях над плоской поверхностью. Т. е. капиллярная конденсация происходит при более низких, чем $p_0$, давлениях.
Искривление поверхности жидкости может существенно влиять на процессы испарения, кипения, растворения, зародышеобразования при конденсации пара и кристаллизации. Так, свойства систем, содержащих большое количество капель или пузырьков газа (эмульсий, аэрозолей, пен), и их формирование во многом определяются К. я. Они лежат также в основе мн. технологич. процессов: флотации, спекания порошков, вытеснения нефти из пластов водными растворами поверхностно-активных веществ, адсорбционного разделения и очистки газовых и жидких смесей и т. п.
Впервые К. я. были исследованы Леонардо да Винчи. Систематич. наблюдения и описания К. я. в тонких трубках и между плоскими, близко расположенными стеклянными пластинами провёл в 1709 Ф. Хоксби, демонстратор Лондонского королевского об-ва. Основы теории К. я. заложены в трудах Т. Юнга, П. Лапласа, а их термодинамич. рассмотрение осуществил Дж. Гиббс (1876).
Источник
Капиллярные явления
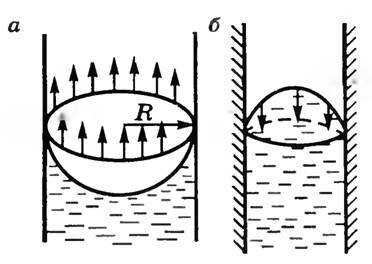
Искривление поверхности жидкости у краев сосуда особенно отчетливо видно в узких трубках, где искривляется вся свободная поверхность жидкости. В трубках с узким сечением эта поверхность представляет собой часть сферы, ее называют мениском. У смачивающей жидкости образуется вогнутый мениск (рис. 1, а), а у несмачивающей — выпуклый (рис. 1, б). Так как площадь поверхности мениска больше, чем площадь поперечного сечения трубки, то под действием молекулярных сил искривленная поверхность жидкости стремится выпрямиться.

Рис. 1
Силы поверхностного натяжения создают дополнительное (лапласово) давление под искривленной поверхностью жидкости.
Для расчета избыточного давления предположим, что поверхность жидкости имеет форму сферы радиуса R (рис. 2. а), от которой мысленно отсечен шаровой сегмент, опирающийся на окружность радиуса r = R sin α.
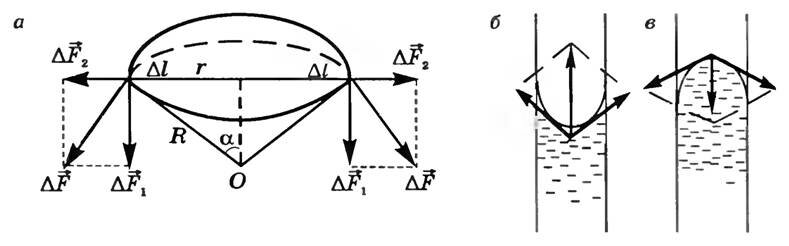
Рис. 2
На каждый бесконечно малый элемент длины Δl этого контура действует касательная к поверхности сферы сила поверхностного натяжения, модуль которой (~Delta F = alpha Delta l). Разложим вектор (~Delta vec F) на две составляющие силы (~Delta vec F_1) и (~Delta vec F_2). Из рисунка 2, а видим, что геометрическая сумма сил
(~Delta vec F_2) для двух выделенных диаметрально противоположных элементов Δl равна нулю. Поэтому сила поверхностного натяжения направлена перпендикулярно плоскости сечения внутрь жидкости (рис. 2, в) и модуль ее равен
(~F = sum Delta F_1 = sum Delta F sin alpha = sum alpha Delta l frac rR = frac{alpha r}{R} sum Delta l = frac{alpha r}{R} cdot 2 pi r = frac{2 alpha pi r^2}{R} .)
Избыточное давление, создаваемое этой силой[~p = frac FS], где S = πr2 — площадь основания сферического сегмента. Поэтому
(~p = frac{2 alpha pi r^2}{R cdot pi r^2} = frac{2 alpha}{R} .)
Если поверхность жидкости вогнутая, то сила поверхностного натяжения направлена из жидкости (рис. 2, б) и давление под вогнутой поверхностью жидкости меньше, чем под плоской, на ту же величину (~p = frac{2 alpha}{R}) . Эта формула определяет лапласово давление для случая сферической формы свободной поверхности жидкости. Она является частным случаем формулы Лапласа, определяющей избыточное давление для произвольной поверхности жидкости двоякой кривизны:
(~p = alpha left( frac{1}{R_1} + frac{1}{R_2} right),)
где R1 и R2 — радиусы кривизны двух любых взаимно перпендикулярных нормальных сечений поверхности жидкости. Радиус кривизны положителен, если центр кривизны соответствующего сечения находится внутри жидкости, и отрицателен, если центр кривизны находится вне жидкости. Для цилиндрической поверхности (R1 = l; R2 = ∞) избыточное давление (~p = frac{alpha}{R}) .
Если поместить узкую трубку (капилляр) одним концом в жидкость, налитую в широкий сосуд, то вследствие наличия силы лапласова давления жидкость в капилляре поднимается (если жидкость смачивающая) или опускается (если жидкость несмачивающая) (рис. 3, а, б), так как под плоской поверхностью жидкости в широком сосуде избыточного давления нет.
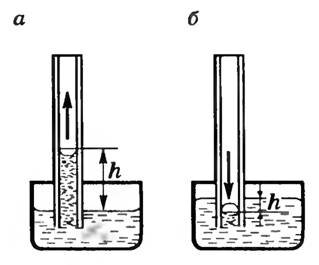
Рис. 3
Явления изменения высоты уровня жидкости в капиллярах по сравнению с уровнем жидкости в широких сосудах называются капиллярными явлениями.
Жидкость в капилляре поднимается или опускается на такую высоту h, при которой сила гидростатического давления столба жидкости уравновешивается силой избыточного давления, т.е.
(~frac{2 alpha}{R} = rho gh .)
Откуда (~h = frac{2 alpha}{rho gR}). Если смачивание не полное θ ≠ 0 (θ ≠ 180°), то, как показывают расчеты, (~h = frac{2 alpha}{rho gR} cos theta).
Капиллярные явления весьма распространены. Поднятие воды в почве, система кровеносных сосудов в легких, корневая система у растений, фитиль и промокательная бумага — капиллярные системы.
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 182-184.
Источник
