Жук ползет по дну сосуда

Задача 9. На плоскости, тангенс угла наклона которой равен коэффициенту трения, лежит монета. В горизонтальном направлении вдоль плоскости монете сообщили скорость v. Найдите установившуюся скорость монеты.

Эта задача со звездочкой, значит трудная (олимпиадная). Сделаем рисунок)

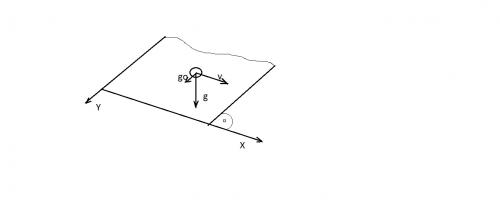
На этом рисунке g направлено вертикально вниз, вектор скорости V вдоль плоскости горизоньально, а вектор g0 это составляющая вектора g на плоскость (g0 = g sin α ). Выберем оси Х и Y.После некоторого времени движение будет установившемся. Запишем уравнения движения по осям.

may = mg sin α – μmg cos α

max = μmg cos α. Откуда ay = g sin α – μg cos α; ax = μg cos α. Проекции скоростей имеют вид

 vy = gt sin α – μgt cos α; vx = v – μgt cos α. Сделаем два замечания: условие равновесия монеты в исходном состоянии имеет вид μmg cos α = mg sin α, значит μ = tg α. Это условие означает, что ускорение вдоль оси Y отсутствует, а vx примет вид vx = v – gt sin α. Но формально второе выражение есть vy без начальной скорости. Получим: vx = v – vy или (обозначив u = vx = vy  установившуюся скорость), получим u = v / 2. Это ответ. Решение слабое, может, и неверное. Но хотя бы один балл может быть заработан.

Задача 9. Тело, находящееся на горизонтальной плоскости, тянут за нить в горизонтальном направлении. Нарисуйте график зависимости силы трения, действующей на тело со стороны плоскости, от силы натяжения нити. Первоначально тело неподвижно. Масса тела 10 кг, коэффициент трения 0,51

 Сделаем рисунок и расставим силы.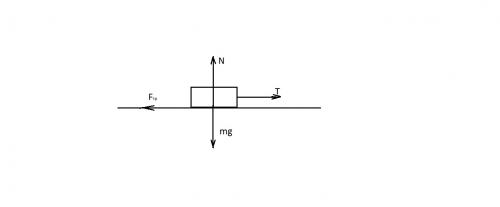

 Сила трения покоя равна Т, чем больше Т, тем больше сила трения. Сила трения будет расти до Fтр макс= μN = =μmg.  Запишем второй закона Ньютона

0 = T – Fтр, откуда Fтр = Т.  Когда начнется

скольжение, Fтр = Fтр макс = const. График будет выглядеть следующим образом:

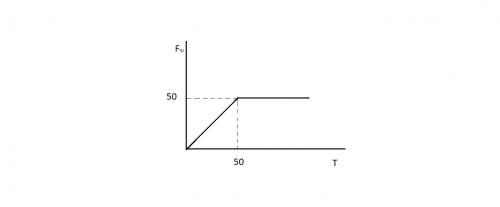
Эта задача уровня В, или даже А

Задача 10. К свободному концу нити, прикрепленной к стенке и переброшенной через ролик, подвешен груз. Ролик закреплен на бруске массы m0,  который может скользить по горизонтальной плоскости без трения. В начальный момент нить с грузом отклоняют от вертикали на угол α и затем отпускают. Определите ускорение бруска, если угол, образованный нитью с вертикалью, не меняется при движении системы

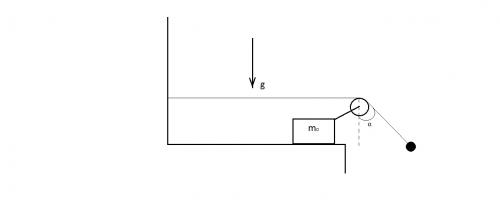
Задача со звездочкой. Сделаем рисунок и расставим силы. Сразу же заметим, что отклонив грузик колебаний не происходит. Почему? Предположим, что система движется влево с ускорением. Тогда грузик действительно останется в покое в отклоненном состоянии. Видимо, это важное предположение.

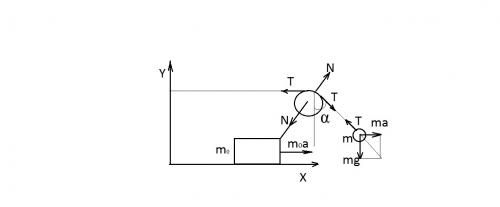
Сила Т – сила натяжения нити, N – сила реакции опоры блока и сила со стороны блока на тело mo. Эти силы обусловлены невесомостью блока и нити, а также нерастяжимости нити. Силы m0a и ma – силы инерции, сила mg – сила тяжести. Тело m0 в покое, т.к. сила инерции m0 компенсируется силой N, котороя, в свою очередь, равна сумме N = T + T (это векторы). Ускорение системы найдем  по формуле

tg α = ma / mg, откуда a = g tg α. Это первый ответ. Спроецируем на горизонтальное направление уравнение движения. В движущейся неинерциальной системе тело mo в покое, значит

0 = m0a – T + Tsin α. Подставим значение ускорения и силы Т = mg /cos α получим m0ag·tg α = mg(1 / cos α – tg α)  , из которого найдем массу m = m0 sin α /(1 – sin α).  Это второй ответ, который, к сожалению не совпал с приведенным в задачнике (m = m0 sin α /(1 – sin α)2 ). Попробуйте найти ошибку или дать другое решение, а меня извините, если я неправильно привел ответ.

 Задача 11. Две заряженные частицы массы mи 2m, равные по модулю импульсы, одновременно вылетают навстречу друг другу из точек А и В. Частицы взаимодействуют только друг с другом. По траектории частицы массы 2m, приведенной на рисунке, восстановите траекторию другой частицы.

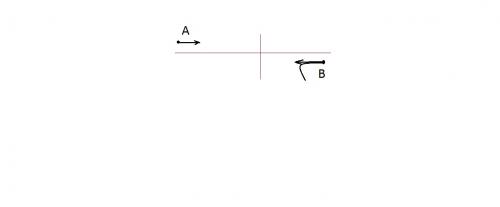
 Это задача качественная. Может в чем-то и полезная. Сделаем рисунок. 

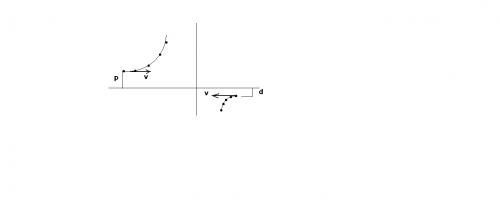
Воспользуемся законом сохранения момента импульса (который в базовой школе не изучается):

mvp = 2mvd, откуда p = 2d, т.е. отклонение левой частицы в 2 раза больше. При d → | – ∞ | p → + ∞. 

Соскучились по задачам со звездочкой?

Задача 12. На гладком полу стоит сосуд, заполненный водой плотностью ρ0; Объем воды V. Оказавшийся на дне сосуда жук объема Vи плотностью ρ через некоторое время начинает ползти по дну сосуда со скоростью uотносительно него. С какой скоростью станет двигаться сосуд по полу? Массой сосуда пренебречь, уровень воды все время остается горизонтальным.          

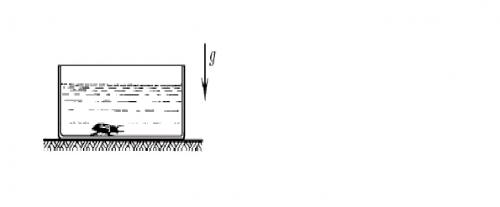
Это задача на движение центра масс. Внешними силами будут вертикальные силы P’ж = Рж – ρ0gV, где Рж = ρgV – сила тяжести жука, N – сила реакции опоры (см. рисунок). На направление оси Х проекции этих сил равны нулю. В начальный момент скорость центра масс равна нулю хс = 0.

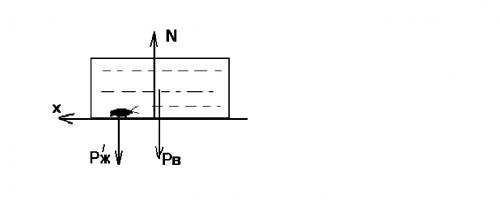
Пусть перемещение сосуда равно ξ2 = x, а перемещение жука равно ξ1 = – (L – x) . Тогда ξ1P’ж + ξ2 Р0  = 0 . Это уравнение (и ему подобное надо запомнить), Оно означает, что если система замкнута, то положение центра масс, даже если тела системы перемещаются, остается неизменным. Запищем последнее равенство в виде: Р0x – P’ж ·(L – х). Решим относительно х:

x = L(ρ – ρ0) /[ρV -ρ0(V0 – V)]. Разделим на время t, получим: v = u(ρ – ρ0)V / (ρV + ρ0V0).  Здесь мы учли, что V << V0.

Задача очень полезна и поучительна. В частности, например, для задачи, когда человек переходит с носа лодки на корму.

Задача 13. На гладкой горизонтальной плоскости находится клин с углом α при основании. Тело массы m, положенное на клин, опускается с ускорением, направленным под углом β > α к горизонтали. Определите массу клина.

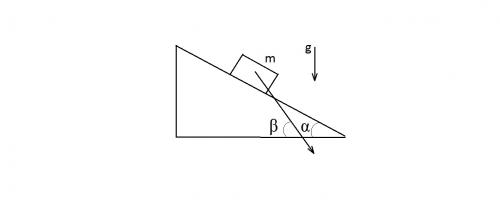
Эта задача без звездочки. Кажется, что ее надо решать стандартно. Однако есть подводные камни. Поступим следующим образом: разложим ускорение тела а0 в горизонтальном направлении a1 и вдоль наклонной плоскости a  (см. рисунок):

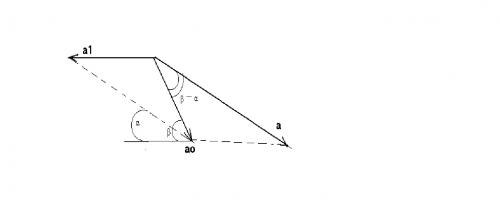
Воспользуемся теоремой синусов: a1 / sin(β – α) = a / sin(π – β).

 Где a1 – ускорение клина, которое возникает под действием тела, а точнее – под действием силы инерции ma cos α.  Т.е. Ma1 = ma cos α.

 Подставляя значение ускорения, получим Ma·sin(β – α) / sin β = ma cos α.

 Откуда, после несложных преобразований, получим M = m tg α / (tg β – tg α).  Это ответ. Надеюсь, что задача полезная в плане обогащения опытом.

Напомню формулу sin(β – α) = sin β cos α – cos β sin α.

Задача 14. Груз массы m, подвешенный на пружине жесткости k, находится на подставке. Пружина при этом не деформирована. Подставку быстро убирают. Определите максимальное удлинение пружины и максимальную скорость груза.  

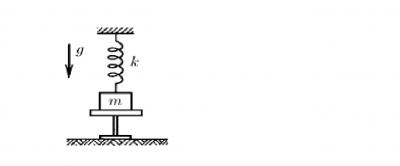
Рассмотрим систему тел – пружину и груз. Запишем изменение потенциальной энергии этой системы.

В начальном состоянии Ep1 = 0. В конечном состоянии Ep2 = kx2 / 2 -mgh.

Полное изменение потенциальной энергии равно нулю, отсюда следует, что

 kx2макс / 2 = mgh, а максимальное удлинение xмкас = 2mg / k.

 Груз под действием пружины начнет колебаться, уравнение колебаний будет иметь вид:

x = xмакс sin ωt, скорость колебаний vмакс = xмакс ω, где ω = (k / m)1/2. Подставляем это значение, получим

vмакс = 2mg / k ·(k / m)1/2 = 2g(m / k)1/2.  Несложная задача.

Задача15. Тело массы m, подвешенное на пружине жесткости k, лежит на доске таким образом, что пружина не деформирована. Доску начинают опускать с ускорением а. Чему равно удлинение пружины в момент отрыва тела от доски?  Каково максимальное удлинение пружины?

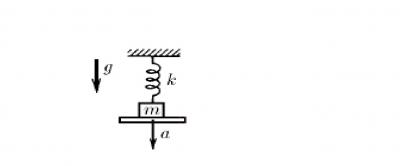
Опять задача со звездочкой. Она решается вполне стандартно. Но пришлось потратить на нее немалое время. Сделаем рисунок и расставим силы. На тело действуют силы упругости, сила реакции опоры, сила тяжести. Само тело движется ускоренно. Запишем второй закон Ньютона: ma = mg – N -kx. 

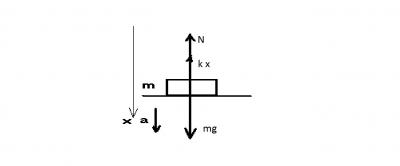
В момент отрыва N = 0, тогда удлинение в момент отрыва составит

    x = m(g – a)/g                                             (1)

Найдем скорость тела в момент отрыва: x = v2/2a, откуда с учетом (1), получим   

v2  = 2am(g – a) / k.                                        (2) 

После отделения подставки тело, за счет инертности, продолжит движение до тех пор, пока не остановится. Пусть оно остановится в точке x0.

Поскольку диссипативных сил нет и внешние силы отсутствуют, то полная энергия после отделения подставки, остается постоянной. Найдем изменения энергии тел, входящих в систему. Изменение кинетической энергии тела равно:

 ΔEk = 0 – mv2/2 = – mv2/2.

Изменение потенциальной энергии тела: ΔEp1 = – mg(x0 – x).  Знак ” – ” означает убыль потенциальной энергии тела.

Изменение потенциальной энергии пружины составит: ΔEp2 = kx02 /2 – kx2 /2. Сумма этих изменений энергий равна нулю:

ΔEk + ΔEp1 + ΔEp2 = 0. Подставляя эти значения, после некоторых алгебраических преобразований, получим квадратное уравнение:

 x20 – (2mg/k)·x0 – 2m2ag/k2 + m2a2/k2 + m2g2/k2 = 0

Решение которого и даст наибольшее отклонение: x0 = m(g + √2ag -a2) / k.  Это второй ответ. Конечно,  эта задача высокого уровня или олимпиадного. Но тренироваться надо на трудных задачах.

Задача 16. На горизонтальной плоскости лежат два бруска массы m1 и m2, соединенных недеформированной пружиной. Определите, какую наименьшую постоянную силу нужно приложить к левому бруску, чтобы сдвинулся и правый, если коэффициент трения грузов о плоскость µ.

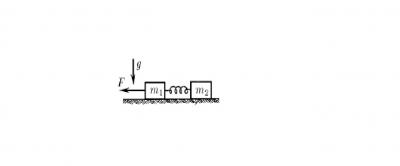 Делать рисунок не будем. Будем считать, что скорость перемещения первого тела небольшая, тогда работа внешней силы F и работа силы трения, действующей на первое тело равно изменению потенциальной энергии пружины ΔEp = A – Aтр.  Или kx2/2 = Fx – μm1gx,  откуда  kx = 2F -2μm1g. С другой стороны, условие трогания с места второго тела является  kx ≥ μm2g. С учетом этого наибольшая сила равна

2F = 2μm1g + μm2g или F = μg(m1 + m2/2) . Подумайте, почему надо найти именно наименьшую силу.

Задача 17. На каком минимальном расстоянии от места закругления склона должна располагаться стартовая площадка лыжников, чтобы они, достигнув закругления, начали свободный полет? Угол склона α, радиус его закругления R, коэффициент трения между лыжами и снегом μ < tg α. Стартовой скоростью лыжников пренебречь.

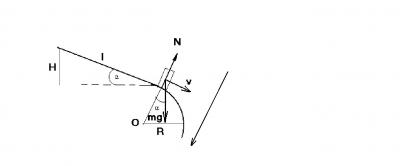 Похожие задачи встречаются в ЕГЭ (Я видел задачу, когда тело въезжает на наклонную плоскость, а затем по закруглению). Эта задача на стыке динамики и закона сохранения энергии. Сделаем рисунок и расставим силы.

 Запишем второй закон Ньютона на направление, указанное стрелкой: maц = mgcosα – N или mv2/R = mgcosα – N. Выразим силу реакции опоры N = mg cosα – mv2/R. Свободный полет будет тогда, когда сила реакции опоры обратится в нуль (N = 0).

 Из этого условия найдем скорость v2 =gR cosα или v = √ gR cosα. Запишем для лыжника значение потенциальной и кинетической энергий в начальном и конечном положениях.

 Ep1 = mgh, Ek1 = 0, Ep2 = 0, Ek2 = mv2/2. Изменения этих энергий равны ΔEp = – mgh, ΔEk = mv2/2. Т.к. ΔEp + ΔEk = – Aтр

т.е. mv2/2 – mgh = – μmgl cos α. Здесь Fтр = μmg cos α, Aтр = – Fтрl.

Это ответ. Теперь становится ясным, почему в задаче оговорено условие  А в самом деле почему?