В сосуде находится газ неон

Решебник
ВСЕ
ФИЗИКА
МАТЕМАТИКА
ХИМИЯ
Задача по физике – 8862
В одном сосуде находятся $10^{19}$, в другом $4 cdot 10^{18}$ молекул одного и того же газа. Сосуды приводят в тепловой контакт. Вначале внутренняя энергия газа в первом сосуде была на 1,9 Дж больше, чем во втором. В конечном состоянии средняя энергия одной молекулы уменьшилась на 25%. Какова внутренняя энергия газа в первом сосуде в конечном состоянии? Теплообменом с окружающими телами пренебречь.
Подробнее
Задача по физике – 8863
Определите работу, совершаемую 1 молем газа в замкнутом цикле, показанном на рис. Температуры в точках 1 и 3 равны соответственно $T_{1}$ и $T_{2}$. Точки 2 и 4 лежат на одной изотерме.

Подробнее
Задача по физике – 8864
Состояние идеального газа изменяется по закону $p = alpha V$. Найдите работу моля идеального газа при повышении его температуры от $T_{1}$ до $T_{2}$.
Подробнее
Задача по физике – 8865
При расширении одноатомного газа его давление растет по линейному закону $p = alpha V$. Определите совершаемую при этом газом работу и изменение его внутренней энергии. Начальные давление и объем газа $p_{1}, V_{1}$, а конечные $p_{2}, V_{2}$.
Подробнее
Задача по физике – 8866
В сосуде находится газ неон, который изобарно расширяется. К нему было подведено количество теплоты 100 кДж. Чему равна работа расширения? На какую величину изменится внутренняя энергия неона?
Подробнее
Задача по физике – 8867
В цилиндре под невесомым поршнем, находящемся на высоте 20 см, содержится воздух. Площадь поршня $100 см^{2}$. Какую работу необходимо совершить, чтобы поднять поршень на 30 см? Атмосферное давление $10^{5} Па$. Температура воздуха постоянна.
Подробнее
Задача по физике – 8868
Определите КПД тепловой машины, работающей по циклу, изображенному на рис. В качестве рабочего вещества используется азот. Масса газа 14 г. Сравните с КПД идеальной тепловой машины. Считать, что температуры нагревателя и холодильника равны соответственно максимальной и минимальной температурам данного цикла.

Подробнее
Задача по физике – 8869
Чему равны теплоемкость одного моля одноатомного идеального газа при изобарном и изохорном процессах?
Подробнее
Задача по физике – 8870
Одноатомный газ, имеющий постоянную массу, может переходить из состояния 1 в состояния А, В и С (рис.). При этом $T_{C} = T_{B}, V_{A} = V_{B}, T_{1} = T_{2}$. Сравните для каждого из этих процессов совершаемые газом работы, изменения внутренней энергии и количества теплоты, сообщаемые газу.

Подробнее
Задача по физике – 8871
Моль идеального одноатомного газа, первоначально находившегося при нормальных условиях, переводят в состояние $p_{2} = 2p_{0}$ с помощью изобарного и изохорного процессов. Газу передано количество теплоты $Q$. Определите конечную температуру газа $T_{2}$, если начальная температура была $T_{0}$.
Подробнее
Задача по физике – 8872
Моль идеального газа нагревается при постоянном давлении, а затем при постоянном объеме переводится в состояние с температурой 300 К, которая равна начальной. Газу при этом сообщили количество теплоты $2,27 cdot 10^{4} Дж$. Во сколько раз изменился объем газа?
Подробнее
Задача по физике – 8873
Вычислите работу, совершаемую одним молем газа в круговом процессе, показанном на рис., если $p_{2}/p_{1} = 2, T_{1} = 280 К$ и $T_{2} = 360 К$.

Подробнее
Задача по физике – 8874
Идеальный одноатомный газ, занимавший объем $2 м^{3}$, расширяется. При этом на p-V-диаграмме расширение описывается прямой линией. Начальное давление $10^{5} Па$. Определите объем газа в конце расширения, если известно, что газ совершил работу $1,1 cdot 10^{5} Дж$.
Подробнее
Задача по физике – 8875
Относительная влажность воздуха при температуре $20^{ circ} С$ равна 20%. Насколько должна увеличиться масса воды в одном кубометре воздуха, чтобы выпала роса? Давление насыщенных паров при этой температуре 2,33 кПа.
Подробнее
Задача по физике – 8876
Вычислите отношение масс $1 м^{3}$ сухого воздуха и $1 м^{3}$ воздуха с влажностью 70% при температуре $20^{ circ} С$ и атмосферном давлении $1,013 cdot 10^{5} Па$. Давление насыщенных паров при этой температуре равно 2,33 кПа. Молярная масса воздуха 0,029 кг/моль.
Подробнее
Источник
Задача по физике – 8854
В расположенном вертикально цилиндре переменного сечения между закрепленными поршнями находится $n$ молей воздуха. Массы поршней $m_{1}$ и $m_{2}$, площади сечений $S_{1}$ и $S_{2}$. Поршни соединены стержнем длиной $l$ и закреплены на одинаковом расстоянии от стыка (рис.). Насколько переместятся поршни, если убрать крепления?

Подробнее
Задача по физике – 8855
Поршень массой 1 кг делит объем сосуда, расположенного вертикально, на части в отношении 1 : 2. С каким ускорением должен двигаться сосуд, чтобы поршень делил сосуд ровно пополам? Давление в нижней половине сосуда равнялось 1,5 атм. Площадь поршня 0,05 $м^{2}$.
Подробнее
Задача по физике – 8856
Цилиндрический сосуд расположен под углом $30^{ circ} С$ к горизонту. В сосуде находится поршень, обладающий теплоизоляционными свойствами и делящий сосуд пополам. Массы газа в обеих половинах сосуда одинаковы. Определите отношение температур газа в обеих половинах сосуда, если давление в нижней половине сосуда 1 атм, площадь поршня $80 см^{2}$, а его масса 2 кг.

Подробнее
Задача по физике – 8857
Сосуд с поршнем, к которому с наружной стороны прикреплен стержень, вращаются в горизонтальной плоскости с угловой скоростью 10 рад/с. Поршень находится в цилиндре, площадь поперечного сечения поршня и цилиндра $50 см^{2}$. Масса поршня 1 кг. Длина стержня 60 см. При горизонтальном положении сосуда в неподвижном состоянии поршень находится от дна сосуда на расстоянии 20 см. На какое расстояние перемещается поршень относительно дна сосуда при вращении сосуда? Считать, что во время движения стержень не деформируется.
Подробнее
Задача по физике – 8858
Поршень массой $m$ лежит на пружине, прикрепленной ко дну сосуда. Под поршнем газ отсутствует. Какая должна быть масса газа $m_{x}$, заполняющего сосуд под поршнем, чтобы деформация пружины была такой же по величине, но пружина растянута? Температура газа $T$, атмосферное давление $p_{атм}$. В недеформированном состоянии длина пружины $l_{0}$, площадь поперечного сечения сосуда и поршня $S$, молярная масса газа $M$, жесткость пружины $k$.
Подробнее
Задача по физике – 8859
Цилиндрический сосуд высотой $H$ разделен на две половины перегородкой. В перегородке есть отверстие, закрытое пробкой. В верхней половине находится вода, в нижней — воздух при атмосферном давлении $p_{0}$. Пробку вынимают, и вода начинает выливаться из верхней половины в нижнюю. Каким будет уровень воды в нижней половине сосуда, когда пузырьки воздуха начнут двигаться по водному слою вверх? Температуру считать постоянной, плотность воды $p$.
Подробнее
Задача по физике – 8860
На пути молекулярного пучка находится стенка. Найдите давление, испытываемое при этом стенкой, если скорость молекул $10^{3} м/с$, их концентрация $5 cdot 10^{17} м^{-3}$, а масса молекулы $3,3 cdot 10^{-27} кг$. Стенка движется навстречу пучку со скоростью 50 м/с.
Подробнее
Задача по физике – 8861
В сосуде давление газа во всех точках одинаково. Температуры стенок $T_{1}$ и $T_{2}$. Определите отношение числа соударений молекул со стенками сосуда за один и тот же промежуток времени. Считать, что у стенки температура газа равна температуре стенки.
Подробнее
Задача по физике – 8862
В одном сосуде находятся $10^{19}$, в другом $4 cdot 10^{18}$ молекул одного и того же газа. Сосуды приводят в тепловой контакт. Вначале внутренняя энергия газа в первом сосуде была на 1,9 Дж больше, чем во втором. В конечном состоянии средняя энергия одной молекулы уменьшилась на 25%. Какова внутренняя энергия газа в первом сосуде в конечном состоянии? Теплообменом с окружающими телами пренебречь.
Подробнее
Задача по физике – 8863
Определите работу, совершаемую 1 молем газа в замкнутом цикле, показанном на рис. Температуры в точках 1 и 3 равны соответственно $T_{1}$ и $T_{2}$. Точки 2 и 4 лежат на одной изотерме.

Подробнее
Задача по физике – 8864
Состояние идеального газа изменяется по закону $p = alpha V$. Найдите работу моля идеального газа при повышении его температуры от $T_{1}$ до $T_{2}$.
Подробнее
Задача по физике – 8865
При расширении одноатомного газа его давление растет по линейному закону $p = alpha V$. Определите совершаемую при этом газом работу и изменение его внутренней энергии. Начальные давление и объем газа $p_{1}, V_{1}$, а конечные $p_{2}, V_{2}$.
Подробнее
Задача по физике – 8866
В сосуде находится газ неон, который изобарно расширяется. К нему было подведено количество теплоты 100 кДж. Чему равна работа расширения? На какую величину изменится внутренняя энергия неона?
Подробнее
Задача по физике – 8867
В цилиндре под невесомым поршнем, находящемся на высоте 20 см, содержится воздух. Площадь поршня $100 см^{2}$. Какую работу необходимо совершить, чтобы поднять поршень на 30 см? Атмосферное давление $10^{5} Па$. Температура воздуха постоянна.
Подробнее
Задача по физике – 8868
Определите КПД тепловой машины, работающей по циклу, изображенному на рис. В качестве рабочего вещества используется азот. Масса газа 14 г. Сравните с КПД идеальной тепловой машины. Считать, что температуры нагревателя и холодильника равны соответственно максимальной и минимальной температурам данного цикла.

Подробнее
Источник
11. МКТ и Термодинамика (объяснение явлений)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
На рисунке показана зависимость давления газа (p) от его плотности (rho) в циклическом процессе, совершаемом 2 моль идеального газа в идеальном тепловом двигателе. Цикл состоит из двух отрезков прямых и четверти окружности.
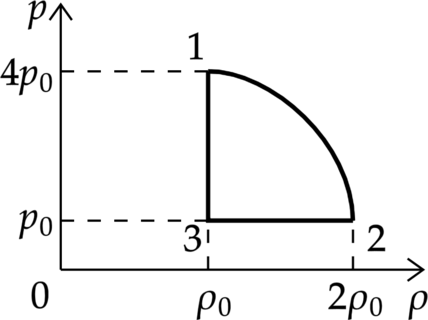
На основании анализа этого циклического процесса выберите два верных утверждения.
1) В процессе 1−2 температура газа уменьшается.
2) В состоянии 3 температура газа максимальна.
3) В процессе 2−3 объём газа уменьшается.
4) Отношение максимальной температуры к минимальной температуре в цикле равно 8.
5) Работа газа в процессе 3−1 положительна.
“Демоверсия 2017”
1) По уравнению Клапейрона – Менделеева: [p=dfrac{rho}{mu}RT,] где (T) – температура, (mu) – молярная масса газа.
Давление уменьшилось в 4 раза, а плотность увеличилась в 2 раза, следовательно, температура уменьшилась в 8 раз.
Утверждение 1 – (color{green}{small text{Верно}})
2) Аналогично предыдущему пункту [p=dfrac{rho}{mu}RT] Максимальная температура будет в состоянии 1 (давление максимально, плотность минимальна)
Утверждение 2 – (color{red}{small text{Неверно}})
3) В процессе 2 – 3 плотность меньшается, а по формуле: [rho =dfrac{m}{V}] Объем увеличивается
Утверждение 3 – (color{red}{small text{Неверно}})
4) Аналогично пункту 2, минимальность температуры будет достигнута в точке с наименьшим давлением и наибольшей плотностью (т. 2), а отношение температур действительно равно 8
Утверждение 4 – (color{green}{small text{Верно}})
5) В процессе 2 – 3 плотность постоянна, следовательно, объем постоянен и газ не совершает работу.
Утверждение 5 – (color{red}{small text{Неверно}})
Ответ: 14
Сосуд разделён на две равные по объёму части пористой неподвижной перегородкой. В начальный момент времени в левой части сосуда содержится 4 моль гелия, в правой – 40 г аргона. Перегородка может пропускать молекулы гелия и является непроницаемой для молекул аргона. Температура газов одинаковая и остаётся постоянной. Выберите два верных утверждения, описывающих состояние газов после установления равновесия в системе.
1) Концентрация гелия в правой части сосуда в 2 раза меньше, чем аргона.
2) Отношение давления газов в правой части сосуда к давлению газа в левой части равно 1,5.
3) В правой части сосуда общее число молекул газов меньше, чем в левой части.
4) Внутренняя энергия гелия и аргона одинакова.
5) В результате установления равновесия давление в правой части сосуда увеличилось в 3 раза.
“Демоверсия 2020”
Перегородка проницаема только для молекул гелия, поэтому в результате установления равновесия парциальное давление гелия в левой части будет равно парциальному давлению гелия в правой части. Давление газа можно вычислить по формуле: [p=dfrac{nu R T}{V}] Парциальные давления гелия в левой и правой части одинаковы, одинаковы температуры и объёмы частей, следовательно, одинаковы и количества вещества гелия в левой и правой частях сосуда, то есть в левой и правой части сосуда будет содержаться по 2 моля гелия.
Найдём связь концентрации и количества вещества: [n=dfrac{N}{V}=dfrac{nu N_A}{V}] То есть концентрации и количества вещества зависят прямо пропорционально друг от друга, также заметим, что чем больше количество вещества, тем больше и количество молекул.
Найдём количество вещества аргона: [nu_{Ar}=dfrac{m_{Ar}}{mu_{Ar}}=dfrac{40text{ г}}{40text{ г/моль}}=1text{ моль}]
Используя полученное выше, рассмотрим данные в задании утверждения.
Концентрация гелия в два раза больше концентрации аргона в правой части сосуда
1) (color{red}{small text{Неверно}})
Концентрация гелия в два раза больше концентрации аргона в правой части сосуда
2) (color{green}{small text{Верно}})
Отношение давлений: [dfrac{p_text{ п}}{p_text{ л}}=dfrac{nu_text{ г.п}+nu_{Ar}}{nu_text{ г.л}}=dfrac{2text{ моль}+1text{ моль}}{2text{ моль}}=1,5] Где (nu_{text{ г.п.}},nu_{text{ г.л.}}) – количество вещества гелия в правой части, количество вещества гелия в левой части соответственно.
3) (color{red}{small text{Неверно}})
Количество вещества газов в правой части сосуда больше количества вещества газа в левой части сосуда, следовательно, в правой части сосуда общее число молекул газа больше, чем в левой части сосуда.
4) (color{red}{small text{Неверно}})
Внутренняя энергия одноатомного идеального газа может быть вычислена по формуле: [U=dfrac{3}{2}nu R T] Температура газов одинакова. Количество вещества гелия больше количества вещества аргона, следовательно, внутренняя энергия гелия больше внутренней энергии аргона.
5) (color{green}{small text{Верно}})
айдём отношение конечного давления в правой части сосуда к начальному давлению в правой части сосуда: [dfrac{p_{k}}{p_text{ н}}=dfrac{nu_{text{ г.п.}}+nu_{Ar}}{nu_{Ar}}=dfrac{2text{ моль}+1text{ моль}}{1text{ моль}}=3]
Ответ: 25
В цилиндрическом сосуде под поршнем находится газ. Поршень может перемещаться в сосуде без трения. На дне сосуда лежит стальной шарик (см. рисунок). Газ нагревают.
Выберите из предложенного перечня два верных утверждения, верно описывающие данный процесс, и укажите их номера.
1) Объём газа в этом процессе остаётся неизменным.
2) Давление газа в сосуде остаётся неизменным.
3) Плотность газа в этом процессе увеличивается.
4) Сила Архимеда, действующая на шарик, уменьшается.
5) Концентрация молекул газа в сосуде увеличивается.
1) Так как поршень подвижный (не закреплен), то процесс будет происходить при постоянном давлениии.
Уравнение состояния газа: [pV=nu RT] где (nu) — количество вещества, (T) — температура в Кельвинах, (p) — давление газа, (V) — объем, занимаемый газом, (R) — универсальная газовая постоянная. Выразим объем [V=dfrac{nu RT}{p}] При нагревании газа объем увеличивается.
Утверждение 1 — (color{red}{smalltext{Неверно }})
2) Утверждение 2 — (color{green}{smalltext{Верно }})
3) Плотность газа: [rho=dfrac{m}{V}] При нагревании объем увеличивается, значит плотность уменьшается.
Утверждение 3 — (color{red}{smalltext{Неверно }})
4) Сила Архимеда: [F_{text{Арх}}=rho gV] где (rho) — плотность газа, (V) — объем шарика, (g) — ускорение свободного падения. Плотность уменьшается, значит, сила Архимеда уменьшается.
Утверждение 4 — (color{green}{smalltext{Верно }})
5) Концентрация: [n=dfrac{N}{V}] При нагревании газа объем увеличивается, концентрация уменьшается.
Утверждение 5 — (color{red}{smalltext{Неверно }})
Ответ: 24
На (pV)—диаграмме отображена последовательность трёх процессов (1 — 2 — 3) изменения состояния 2 моль идеального газа. 
Из предложенного перечня утверждений выберите два правильных и укажите их номера.
1) В процессе 1 газ отдаёт положительное количество теплоты.
2) Процесс 2 является изотермическим.
3) В процессе 3 газ совершает работу.
4) В процессе 2 происходит расширение газа при постоянной температуре.
5) В процессе 1 происходит сжатие газа при постоянной температуре.
Работа газа находится как площадь под графиком 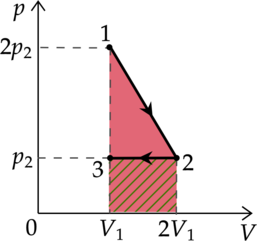
1) Первое начало термодинамики: [Q=Delta U+A] где (Delta U) — изменение внутренней энергии, (A) — работа газа, (Q) — количество теплоты, полученное газом. (Delta U=0), так как температура в процессе 1 не изменяется. При увеличении давления в изотермическом процессе объём уменьшается. (Delta V<0), следоватлеьно, (A<0). Таким образом, (Q<0), то есть газ отдает кол-во теплоты в данном процессе.
Утверждение 1 — (color{green}{smalltext{Верно }})
2) В процессе 2 температура увеличивается.
Утверждение 2 — (color{red}{smalltext{Неверно }})
3) (p=const), следовательно (Vsim T)
Температура уменьшается, то есть объем тоже уменьшается, (Delta V<0), (A<0)
Утверждение 3 — (color{red}{smalltext{Неверно }})
4) В процессе 2 температура увеличивается.
Утверждение 4 — (color{red}{smalltext{Неверно }})
5) Температура в процессе 1 не изменяется. По закону Бойля-Мариотта (p V=const) так как давление увеличивается объём уменьшается.
Утверждение 5 —(color{green}{smalltext{Верно }})
Ответ: 15
На рисунке показан график циклического процесса, проведённого с одноатомным идеальным газом, в координатах (V-T), где (V) — объём газа, (T) — абсолютная температура газа. Количество вещества газа постоянно. 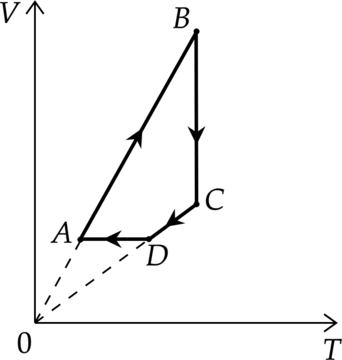
Из приведённого ниже списка выберите два правильных утверждения, характеризующие процессы на графике, и укажите их номера.
1) В состоянии (B) концентрация газа максимальна.
2) В процессе (AB) газ отдаёт некоторое количество теплоты.
3) В процессе (BC) внутренняя энергия газа увеличивается.
4) Давление газа в процессе (CD) постоянно, при этом внешние силы совершают над газом положительную работу.
5) В процессе (DA) давление газа изохорно уменьшается.
1) В точке (B) объем максимален, а концентрация минимальна:
Утверждение 1 —(color{red}{smalltext{Неверно }})
2) Первое начало термодинамики: [Q=Delta U+A] где (Delta U) — изменение внутренней энергии, (A) — работа газа, (Q) — количество теплоты, полученное газом. В процессе (AB) работа равна (0), температура увеличивается, то есть (Delta U>0), значит (Q>0), то есть газ получает тепло
Утверждение 2 — (color{red}{smalltext{Неверно }})
3) Процесс (BC) — изотермический. Внутренняя энергия не меняется.
Утверждение 3 — (color{red}{smalltext{Неверно }})
4) Процесс (СD) — изобарное сжатие. При уменьшении объема внешние силы совершают положительную работу.
Утверждение 4 — (color{green}{smalltext{Верно }})
5) Процесс (DA) — изохорное охлаждение ((psim T)). Следовательно, при уменьшении температуры давление уменьшается.
Утверждение 5 — (color{green}{smalltext{Верно }})
Ответ: 45
Идеальный газ перевели из состояния 1 в состояние 3 так, как показано на графике зависимости давления р газа от объёма V. Количество вещества газа при этом не менялось. 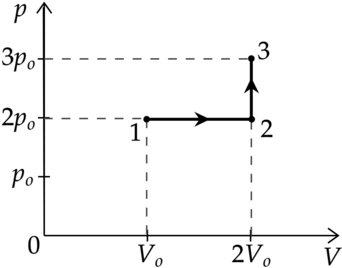
Из приведённого ниже списка выберите два правильных утверждения, характеризующие процессы на графике.
1)Абсолютная температура газа минимальна в состоянии 2.
2)В процессе 1-2 абсолютная температура газа уменьшилась в 2 раза.
3)В процессе 2-3 абсолютная температура газа уменьшилась в 1,5 раза.
4)Плотность газа максимальна в состоянии 1.
5)В ходе процесса 1-2-3 средняя квадратичная скорость теплового движения молекул газа увеличилась в (sqrt{3}) раза.
1) Уравнение состояния газа: [pV=nu RT] где (p) — давление газа, (V) — объем, занимаемый газом, (nu) — количество вещеста, (R) — универасальная газовая постоянная, (T) — температура. Температура максимальна там, где максимально произведение (pV), поэтому из графика видно, что (T_1 – min), (T_3 – max), (T_1<T_2<T_3)
Утверждение 1 — (color{red}{smalltext{Неверно }})
2) Процесс 1-2 — изобарное расширение ((Vsim T)). Объем увеличился в 2 раза, то есть температура тоже увеличилась в 2 раза.
Утверждение 2 — (color{red}{smalltext{Неверно }})
3) Процесс 2-3 — изохорное нагревание. (V=const), следовательно (psim T) Давление увеличивается в 1,5 раза, то есть температура тоже увеличивается в 1,5 раза.
Утверждение 3 — (color{red}{smalltext{Неверно }})
4) В точке 1 — объем минимален, следовательно, плотность там максимальна.
Утверждение 4 — (color{green}{smalltext{Верно }})
5) [E_{k}=dfrac{3}{2}kT] [dfrac{m_0 v^2}{2}=dfrac{3}{2}kT] где (m_0) — масса газа, (v^2) средняя квадратичная скорость [v^2sim T] [vsim sqrt{T}] Температура в процессе 1-2-3 увеличилась в 3 раза, значит средняя квадратичная скорость увеличилась в (sqrt{3}) раз
Утверждение 5 — (color{green}{smalltext{Верно }})
Ответ: 45
Сосуд разделён на две равные по объёму части пористой неподвижной перегородкой. В левой части сосуда содержится 40 г неона, в правой — 2 моль гелия. Перегородка может пропускать молекулы гелия и является непроницаемой для молекул неона. Температура газов одинакова и остаётся постоянной.
Выберите два верных утверждения, описывающих состояние газов после установления равновесия в системе.
1) Внутренняя энергия гелия в сосуде меньше, чем внутренняя энергия неона.
2) Концентрация гелия в левой части сосуда в 2 раза больше концентрации неона.
3) В левой части сосуда общее число молекул газов в 3 раза больше, чем в правой части.
4) Внутренняя энергия гелия в сосуде в конечном состоянии меньше, чем в начальном.
5) В конечном состоянии давление в левой части сосуда в 3 раза больше, чем в правой.
1) Молярная масса неона (M=20) г/моль. Количество неона: [nu=dfrac{m}{M}=dfrac{40text{ г}}{20text{ г/моль}}=2 text{ моль}] Гелий займет все пространство сосуда, значит в левой части будет 3 моля вещества (1 моль гелия и 2 моль неона).
В правой части будет тоже 1 моль гелия.
Внутренняя энергия газа: [U=dfrac{i}{2}nu RT] Газы находятся при одинаковой температуре, количество гелия равно количеству неона. Внутренняя энергия гелия равна внутренней энергии неона
Утверждение 1 — (color{red}{smalltext{Неверно }})
2) В левой части сосуда количество гелия в два раза меньше количества неона. Следовательно, концентрация гелия в два раза меньше концентрации неона.
Утверждение 2 — (color{red}{smalltext{Неверно }})
3) Так как количество вещества в левой части сосуда больше в 3 раза, чем в правой, то и количество молекул также больше в 3 раза.
Утверждение 3 — (color{green}{smalltext{Верно }})
4) Так как температура гелия и общее количество гелия в сосуде не изменилось, то и внутреннняяя энергия не поменялась.
Утверждение 4 — (color{red}{smalltext{Неверно }})
5) Давление газа: [p=nkT] Так как кол-во вещества в левой части сосуда больше в 3 раза, чем в правой, температуры одинаковые, то давление в конечном состоянии больше в левой части в 3 раза, чем в правой.
Утверждение 5 — (color{green}{smalltext{Верно }})
Ответ: 35
Источник
