В три сосуда различной формы налили жидкость таким образом чтобы
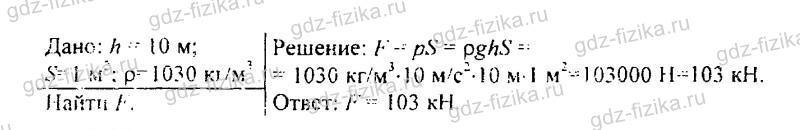
В
заданиях ЕГЭ по математике встречаются задачи, в которых речь идёт о
погружении детали в жидкость или о переливании жидкости из одного сосуда
в другой.
Вопросы
в условии связаны с нахождением объёма погружаемого в жидкость тела или
с нахождением какого-либо параметра сосуда. Форма сосуда может быть
различной: цилиндр, призма.
Что необходимо понимать?
Если
жидкость залита в цилиндрический сосуд, то она принимает форму
цилиндра. Если она залита в имеющий форму призмы, то соответственно
принимает форму призмы. Это означает, что формулы для объёмов цилиндра и
призмы работают и для объёмов жидкостей помещённых в такие сосуды.
Формула объёма (цилиндра и призмы):
Если
жидкость перливается в аналогичный сосуд с меньшим основанием, уровень
(высота) жидкости увеличивается; если в сосуд с большим основанием, то
уровень жидкости уменьшается.
Рекомендации!
В
задачах на погружение детали в жидкость следует найти объём полученный
после её погружения, далее найти разность объёмов до и после (если
данные в условии это позволяют). Можно такие задачи решать и другим
способом, используя закон Архимеда. Примеры рассмотрены ниже.
В
задачах, где идёт речь о переливании жидкости в другой сосуд (с
уменьшенной или увеличенной площадью основания) помните о том, что сам
объём жидкости остаётся неизменным. Вы можете выразить его через площадь
основания и высоту (S1 и H1) одного сосуда и площадь основания и высоту (S2 и H2) другого сосуда, далее полученные выражения приравнять.
При
дальнейших преобразованиях получите отношение соответствующих величин –
либо площадей оснований, их рёбер, либо высот. Пример такой задачи
рассмотрен ниже в статье.
В цилиндрический сосуд налили 5000 см3
воды. Уровень жидкости оказался равным 40 см. В воду полностью
погрузили деталь. При этом уровень жидкости в сосуде поднялся на 15 см.
Чему равен объем детали? Ответ выразите в см3.
Мы знаем, что объём цилиндра равна произведению площади основания на высоту:
В
жидкость погружаем деталь. Её уровень поднимается. Для того, чтобы
вычислить объём детали необходимо из полученного объёма (полученного
после погружения детали) вычесть объём жидкости, который был изначально.
Высота это есть уровень жидкости.
Итак, из имеющихся данных можем найти площадь основания:
Основание
цилиндра у нас величина неизменная, но изменилась высота жидкости (при
погружении детали) на 15 сантиметров, то есть она стала
40 +15 = 55 см.
Найдём полученный объём:
Теперь можем вычислить объём детали: 6875 – 5000 = 1875 см3
Можно решать подобные задачи более рациональным способом.
По закону Архимеда объем детали равен объему вытесненной ею жидкости. Объем вытесненной жидкости равен 15/45 исходного объема:
Ответ: 1875
Решить самостоятельно:
Посмотреть решение
В сосуд, имеющий форму правильной треугольной призмы, налили 2500 см3 воды
и полностью в нее погрузили деталь. При этом уровень жидкости в сосуде
поднялся с отметки 20 см до отметки 24 см. Чему равен объем детали?
Ответ выразите в см3.
Принцип решения тот же самый, что и в предыдущей задаче.
Мы знаем, что объём призмы равен произведению площади основания на высоту:
В
жидкость погружаем деталь. Её уровень поднимается. Для того, чтобы
вычислить объём детали необходимо из полученного объёма (полученного
после погружения детали) вычесть объём жидкости, который был изначально.
Из имеющихся данных можем найти площадь основания призмы:
Основание призмы не изменилось, но изменилась высота жидкости (при погружении детали) она стала 24см.
Найдём полученный объём:
Теперь можем вычислить объём детали: 3000 – 2500 = 500 см3
Второй способ:
По закону Архимеда объем детали равен объему вытесненной ею жидкости. Объем вытесненной жидкости равен 4/20 исходного объема:
Ответ: 500
Решить самостоятельно:
Посмотреть решение
В
сосуд, имеющий форму правильной треугольной призмы, налили воду.
Уровень воды достигает 250 см. На какой высоте будет находиться уровень
воды, если ее перелить в другой такой же сосуд, у которого сторона
основания в 5 раз больше, чем у первого? Ответ выразите в см.
В
подобных задачах с переливаниями жидкости следует помнить, что объём её
остаётся прежним (он не изменен – куда бы её не перелили).
Объем
жидкости в данном случае это объём правильной треугольной призмы (в
её основании лежит правильный треугольник). Он равен произведению
площади основания призмы на высоту:
Суть
дальнейших действий сводится к тому, что мы можем выразить объёмы
жидкостей в двух призмах: первой и второй (основание которой в 4 раза
больше), а затем приравнять полученные выражения, в итоге после
преобразований получим отношение двух высот.
Естественно, что высота жидкости уменьшится, если увеличить площадь основания.
Обозначим исходную высоту жидкости Н1, полученную после переливания Н2.
Найдём площадь основания призмы, обозначив его сторону как а. Площадь правильного треугольника равна:
Таким образом, объём залитой жидкости в первую призму равен:
Площадь основания второй призмы равна:
Объём залитой жидкости во вторую призму равен:
Найдём отношение высот:
Таким образом, при том же объёме жидкости её высота уменьшится в 25 раз и будет равна 10.
Или можно сказать так:
При увеличении стороны основания а в 5 раз уровень воды уменьшится в 25 раз.
Ответ: 10
Решить самостоятельно:
Посмотреть решение
В
цилиндрический сосуд, в котором находится 14 литров воды, опущена
деталь. При этом уровень жидкости в сосуде поднялся в 1,1 раза. Чему
равен объем детали? Ответ выразите в литрах.
Объём цилиндра равна произведению площади его основания на высоту:
Жидкость в сосуде имеет цилиндрическую объёмную форму.
Уровень
жидкости поднялся в 1,1 раза – означает, что высота цилиндра
увеличилась в 1,1 раза. Исходя из формулы объёма цилиндра понятно, что
при увеличении высоты в 1,1 раза влечёт за собой увеличение объёма также
в 1,1 раза (так как зависимость величин прямопропорциональная).
Это означает, что после погружения детали объём будет равен 14∙1,1 = 15,4 литра.
Таким образом, объём детали будет равен: 15,4 – 14 = 1.4 литра.
Ответ: 1,4
Решить самостоятельно:
Посмотреть решение
Если ход решения сразу не увидели, ставьте вопрос – что можно найти исходя из условия?
Например,
если дан начальный объём и высота жидкости (в сосуде формы призмы или
цилиндра), то мы можем найти площадь основания. Затем, зная площадь
основания и высоту жидкости после погружения детали мы можем найти
полученный объём.
Далее
найти разницу между объёмами не составит труда (это относится к первым
двум задачам). В последней задаче для решения требуется немного
логики.
Источник
Проверка: Каким способом можно осуществить проверку? (Действия с наименованиями)
Задача 5:
На дополнительную оценку. В сосуде с водой на подставках находится цилиндр без дна. Высота выступающей из воды части цилиндра равна . Внутрь цилиндра наливают керосин. Какую высоту должен иметь цилиндр, чтобы его можно было заполнить маслом целиком?
Найти: Решение:
Керосин, наливаемый внутрь цилиндра, будет
вытеснять из него воду. Из условия известно,
что давление столба высотой ( – высота цилиндра)
должно быть равно давлению столба воды высотой
(на глубине нижнего конца цилиндра).
, решив уравнение относительно :
,
Ответ: .
Проверка:
Полный анализ:
1. Что описывается в условии задачи? (В задаче описывается сосуд, в котором находится цилиндр без дна)
2. Можно ли данную ситуацию изобразить графически (рисунок, схема, график)? (см. рис.).
Частный анализ:
1) Что нам известно о цилиндре? (Нам известно, что высота выступающей из воды части цилиндра равна .)
2) Что наливают внутрь цилиндра? (Внутрь цилиндра наливают керосин).
3) Что необходимо найти в задаче? (В задаче необходимо найти, высоту, которую должен иметь цилиндр, чтобы его можно было заполнить маслом целиком).
Поиск решения:
1) Что будет происходить с водой, если в цилиндр будем наливать воду? (Вода будет вытесняться под действием веса керосина)
2) Что можно сказать о давлениях воды и керосина на глубине нижнего конца цилиндра? Почему? (Они будут равны).
3) Чему равно давление керосина? ()
4) Чему равно давление воды? ()
5) Какой вид будет иметь уравнение для искомой величины? ().
6) Чему равна высота цилиндра? ()
Проверка: Каким способом можно осуществить проверку? (Действия с наименованиями)
X. Конспект учебного занятия:
№ | Название этапа | Деятельность учителя | Деятельность ученика |
I | Организационный момент. | Добрый день! Садитесь. | |
II | Предъявление домашнего задания | Сегодня домашнее задание будет заключаться в следующем: вам надо решить задачи, которые напечатаны на листочке, а также дорешить те задачи, которые не успеем решить в классе. Кто желает получить дополнительную оценку, может решить задачу на дополнительную оценку из листка-минимума. | Записывают дом. задание. |
III | Вступительная часть | Сегодня мы с вами будем решать задачи по теме «Давление жидкостей. Сообщающиеся сосуды». Научимся применять наши знания при решении задач разных типов, познакомимся с обобщенным планом решения физических задач. | |
IV | Повторение ранее изученного материала | Сейчас вы напишите небольшую проверочную работу по тому, что мы изучили на прошлых уроках. На выполнение этого задания даю вам 5-7 минут. | Дети пишут проверочную работу. |
V | Изучение нового материала | Откройте тетради и запишите сегодняшнее число и тему урока. Перед вами обобщенный план решения физических задач. Сегодня мы с вами будем пользоваться ими при решении задач. Сейчас мы приступим к решению задач. Тот, кто решит все 4 задач, получит пять. Кто хочет дополнительную оценку может решить 5 задачу. 3 и 4 задачи решаем в парах, а потом обсудим ваши решения все вместе! Первая задача будет на вычисление давления на определенной глубине. См СНВ и оформление задачи №1. Молодцы, мы справились с этой задачей. Сейчас мы попробуем решить задачу потруднее. Здесь главное внимательное чтение условия задачи. См. СНВ и оформление задачи № 2 Хорошо, сейчас вы решаете 3 и 4 задачу в парах. Если у кого-то появятся вопросы по ходу решения, поднимайте руки, и я подойду, мы вместе попытаемся разобраться. См. СНВ и оформление задач №3 и №4 Не забывайте о задаче на дополнительную оценку, она трудная, но вы всегда можете спросить меня, если возникают какие-то вопросы. См. СНВ и оформление задачи №5. | Дети записывают: «Давление жидкостей. Сообщающиеся сосуды» Водолаз в жестком скафандре может погружаться на глубину 250 м, искусный ныряльщик – на 20 м. Определите давление воды в море на этих глубинах. В цилиндрический сосуд налиты ртуть, вода и керосин. Определите общее давление, которое оказывают жидкости на дно сосуда, если объемы всех жидкостей равны, а верхний уровень керосина находится на высоте 12 см от дна сосуда. |
VI | Заключительное слово | Итак, ребята. Чему мы с вами сегодня научились? Итак, оценки за сегодняшний урок….. В следующий раз в начале урока мы проверим с вами решение домашних задач. Всем спасибо, до свидания. | Мы сегодня научились решать задачи разных типов. Познакомились с обобщенным планом решения физических задач. |
XI. Дидактический раздаточный материал:
Проверочная работа:
Вариант 1
1. Напишите схему устройства водопровода.
2. Что будет происходить, если с однородной жидкостью, если открыть кран (см. рис)?
3. Как установятся поверхности разнородной жидкости в сообщающихся сосудах разной формы?
Вариант 2
1. Что такое шлюз?
2. Как установятся поверхности однородной жидкости в сообщающихся сосудах разной формы?
3. В три сосуда различной формы налили жидкость таким образом, чтобы ее уровень был во всех сосудах одинаков. В каком сосуде давление жидкости на дно сосуда больше?
Вариант 3
1. Определите, в какой из трубок находится ртуть, а в какой – вода (см. рис.1).
2. Что произойдет, если в среднее колено сообщающихся сосудов с водой долить воды (см. рис.2)?
3. В сообщающиеся сосуды налили воду и подсолнечное масло. Нарисуйте схематично, как расположатся эти жидкости в сосуде.
Листок-минимум задач по теме:
«Давление жидкости. Сообщающиеся сосуды»
1.  Цилиндрические сосуды уравновешены на весах (рис.1). Нарушится ли равновесие весов, если в них налить воды столько, что поверхность ее установится на одинаковом уровне от дна сосудов? Одинаково ли будет давление на дно сосудов?
Цилиндрические сосуды уравновешены на весах (рис.1). Нарушится ли равновесие весов, если в них налить воды столько, что поверхность ее установится на одинаковом уровне от дна сосудов? Одинаково ли будет давление на дно сосудов?
2. Водолаз в жестком скафандре может погружаться на глубину 250 м, искусный ныряльщик – на 20 м. Определите давление воды в море на этих глубинах.
3. В цилиндрический сосуд налиты ртуть, вода и керосин. Определите общее давление, которое оказывают жидкости на дно сосуда, если объемы всех жидкостей равны, а верхний уровень керосина находится на высоте 12 см от дна сосуда.
4. В цистерне, заполненной нефтью, на глубине 3 м имеется кран, площадь отверстия которого 30 см2. С какой силой давит нефть на кран?
5. В сообщающихся сосудах находится ртуть и вода ( рис.2). Высота столба воды 68см. Какой высоты столб керосина следует налить в левое колено, чтобы ртуть установилась на одинаковом уровне?
6. На дополнительную оценку. В сосуде с водой на подставках находится цилиндр без дна. Высота выступающей из воды части цилиндра равна . Внутрь цилиндра наливают масло. Какую высоту должен иметь цилиндр, чтобы его можно было заполнить маслом целиком?
Задачи для домашней работы:
4. Высота столба воды в стакане 8 см. Какое давление на дно стакана оказывает вода? Какое давление оказывала бы ртуть, налитая до того же уровня?
5. Какую силу испытывает каждый квадратный метр площади поверхности водолазного костюма при погружении в морскую воду на глубину 10м?
6. В левом колене сообщающихся сосудов налита вода, а в правом – керосин. Высота столба керосина 20 см. Рассчитайте, на сколько уровень воды в левом колене ниже верхнего уровня керосина.
XII. Диагностика результативности обучения:
1. Решать следующие задачи:
· Водолаз в жестком скафандре может погружаться на глубину 250 м, искусный ныряльщик – на 20 м. Определите давление воды в море на этих глубинах.
· В цилиндрический сосуд налиты ртуть, вода и керосин. Определите общее давление, которое оказывают жидкости на дно сосуда, если объемы всех жидкостей равны, а верхний уровень керосина находится на высоте 12 см от дна сосуда.
· В цистерне, заполненной нефтью, на глубине 3 м имеется кран, площадь отверстия которого 30 см2. С какой силой давит нефть на кран?
· В сообщающихся сосудах находится ртуть и вода ( рис.1). Высота столба воды 68см. Какой высоты столб керосина следует налить в левое колено, чтобы ртуть установилась на одинаковом уровне?
· Высота столба воды в стакане 8 см. Какое давление на дно стакана оказывает вода? Какое давление оказывала бы ртуть, налитая до того же уровня?
· Какую силу испытывает каждый квадратный метр площади поверхности водолазного костюма при погружении в морскую воду на глубину 10м?
· В левом колене сообщающихся сосудов налита вода, а в правом – керосин. Высота столба керосина 20 см. Рассчитайте, на сколько уровень воды в левом колене ниже верхнего уровня керосина.
Осуществлять проверку различными способами (экспериментально, действия с наименованиями).
XIII. Литература для учителя:
1. Кириллова для чтения по физике: Учеб. пособие для учащихся 6 – 7 кл. ср. шк. /Сост. . – 2-е изд., перераб. – М.: Просвещение, 1986. – 207 с., ил. (стр.67 – 71)
2. развитие самостоятельности школьников в учении в условиях обновления информационной культуры общества: В 2 ч.: Ч. I. Моделирование информационно-образовательной среды учения: Монография / Перм. гос. пед. ун-т. – Пермь, 2003. – 294 с. (стр. 247 – 253)
3. Элементарный учебник физики: Учеб. пособие. В 3 т./Под ред. : Т. 1. Механика. Теплота. Молекулярная физика. – 12-е изд. – М.: ФИЗМАТЛИТ, 2000 г. – 608с. (стр. 293 – 295)
4. Физика: Занимательные материалы к урокам. 7 Кл./ Авт.-сост. . – М.: Изд-во НЦ ЭНАС, 2004. – 120 с. – (Портфель учителя).
5. Остер . – М.: «Росмэн», 1994. – 128 с.
6. Книга для чтения по физике. Часть I. Механика. М.:1985 г.
7. , Иванова задач по физике для 7 – 9 классов общеобразовательных учреждений. – 13-е изд. – М.: Просвещение, 2000. – 224 с.: ил. (стр. 72 – 77).
8. Лукашик олимпиада в 6 – 7 классах средней школы. Пособие для учащихся. – 2-е изд., перераб. И доп. – М.: Просвещение, 1987. – 192с.: ил. (стр. 39 – 45).
| Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 |
Источник
504. Сосуд с жидкостью наклонили (рис. 131). Одинаковое ли давление оказывает после этого жид¬кость на боковые стенки А и В в точках, лежащих на одном горизонтальном уровне?
Жидкость оказывает одинаковое давление на одном горизонтальном уровне везде, в том числе и на стенках А и В (см. рис. 131).
505. Сосуд с водой имеет форму, изображенную на рисунке 132. Одинаково ли давление воды на боковые стенки сосуда на уровне аб?
На уровне ab давление воды на боковые стенки одно и то же (см. рис. 132).
506. Цилиндрические сосуды уравновешены на весах (рис. 133). Нарушится ли равновесие весов, если в них налить воды столько, что поверхность ее установится на одинаковом уровне от дна сосудов? Одинаково ли будет давление на дно сосудов?
Равновесие весов нарушается, так как в разных сосудах различная масса воды. Давление на дно сосуда будет одинаковым, так как высота столба воды в обоих сосудах одна и та же (см. рис. 133)
507. Цилиндрические сосуды уравновешены на весах (см. рис. 133). Мальчик налил в оба сосуда воду одинаковой массы. Нарушилось ли равновесие весов? Одинаково ли будет давление воды на дно сосудов?
Равновесие весов не нарушилось. Давление воды на дно сосуда будет различным, так как уровень налитой воды будет различным (см. рис. 133).
508. В цилиндрический сосуд, частично заполненный водой, опустили деревянный брусок. Изменилось ли давление воды на дно сосуда?
Давление воды на дно увеличилось, так как при опускании в воду деревянного бруска ее уровень поднялся.
509. В трех сосудах с одинаковой площадью дна налита вода до одного уровня (рис. 134). В каком сосуде налито больше воды? Одинаково ли давление на дно в этих сосудах? Почему?
Воды налито больше в крайнем левом сосуде. Давление на дно будет одинаковым во всех трех сосудах, так как везде вода налита до одного уровня (см. рис. 134).
510. Уровень воды в сосудах одинаковый (рис. 135). Будет ли переливаться вода из одного сосуда в другой, если открыть кран?
При открывании крана вода из одного сосуда в другой переливаться не будет, так как уровень воды в сосудах будет одинаковый, а следовательно давление воды на любом уровне так же одинаково (см. рис. 135).
511. Уровень жидкостей в сосудах (см. рис. 135) одинаковый. В левом налита вода, в правом — керосин. Одинаковы ли давления на дно? Одинаковы ли давления на кран? Будет ли переливаться жидкость из одного сосуда в другой, если открыть кран?
Давление воды на дно и на кран больше, чем давление керосина. Объясняется это тем, что плотность воды больше плотности керосина. Если кран открыть, то вследствие разности давлений вода потечет в сосуд с керосином (см. рис. 135).
512. В левой части сосуда над жидкостью находится воздух (рис. 136). Какую высоту столба жидкости следует учитывать при расчете давления на дно сосуда: высоту Н или высоту H1? Ответ объясните.

513. В полиэтиленовый мешок налита вода (рис. 137). Что показывают динамометры: давление или силы, действующие на столики динамометров? Стрелка правого динамометра закрыта листом бумаги. Каково показание правого динамометра? Будут ли изменяться показания динамометров, если воду в мешок доливать (выливать)? Ответы обоснуйте.
Динамометры показывают силы давления жидкости на боковые стенки сосуда с водой. Показания их одинаковы и равны 70Н. Если воду в мешок доливать, то показания динамометров увеличатся, а если воду выливать, то уменьшатся, т.к. увеличится либо уменьшится давление столба жидкости (см. рис.137).
514. Одинаково ли давление воды на дно сосудов (рис. 138)? Чему равно это давление? Изменится ли давление, если воду заменить керосином? Чему оно будет равно в этом случае?

515. Высота столба воды в стакане 8 см. Какое давление на дно стакана оказывает вода? Какое давление оказывала бы ртуть, налитая до того же уровня?
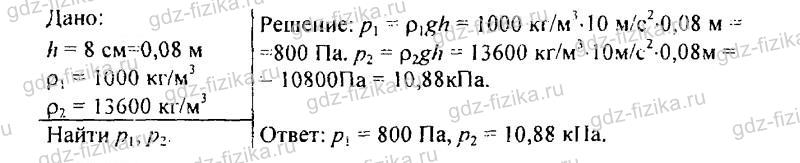
516. Какое давление на дно сосуда оказывает слой керосина высотой 0,5 м?

517. В цилиндрический сосуд налиты ртуть, вода и керосин. Определите общее давление, которое оказывают жидкости на дно сосуда, если объемы всех жидкостей равны, а верхний уровень керосина находится на высоте 12 см от дна сосуда.
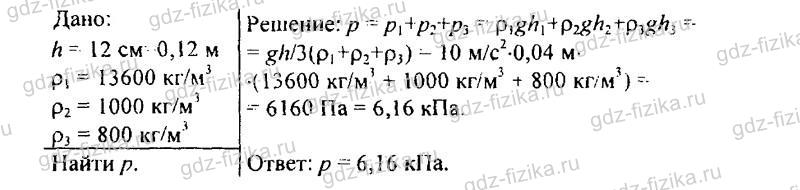
518. Сосуды с водой имеют равные площади дна (рис. 139). В каком из них избыточное давление воды на дно (без учета атмосферного давления) больше и во сколько раз?

519. Водолаз в жестком скафандре может погружаться в море на глубину 250 м, искусный ныряльщик — на глубину 20 м. На сколько и во сколько раз отличаются давления воды на этих глубинах?
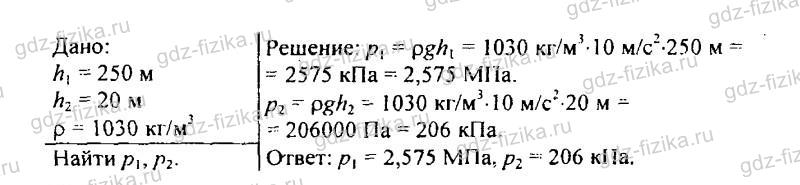
520. Рассчитайте давление воды: а) на самой большой глубине Тихого океана — 11 035 м; б) на наибольшей глубине Азовского моря — 14 м (плотность воды в нем принять равной 1020 кг/м3).
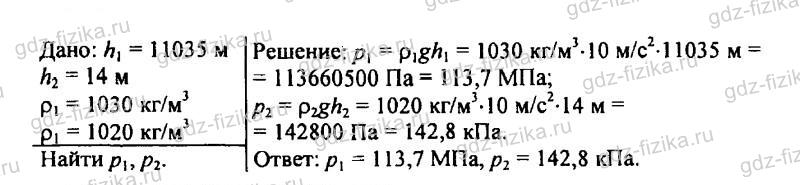
521. Определите по графику (рис. 140) глубину погружения тела в озеро, соответствующую давлению воды 100, 300 и 500 кПа.
10 м; 30 м; 50 м (рис. 140).
522. Аквариум наполнен доверху водой. С какой силой давит вода на стенку аквариума длиной 50 см и высотой 30 см?
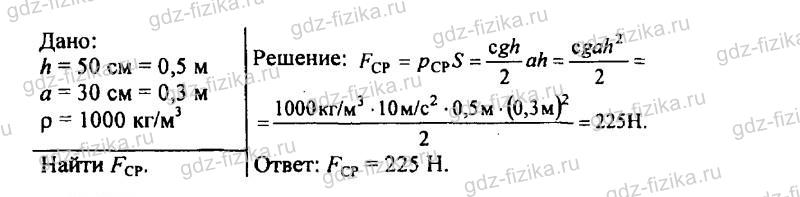
523. В аквариум высотой 32 см, длиной 50 см и шириной 20 см налита вода, уровень которой ниже края на 2 см. Рассчитайте: а) давление воды на дно; б) вес воды; в) силу, с которой вода действует на стенку шириной 20 см.
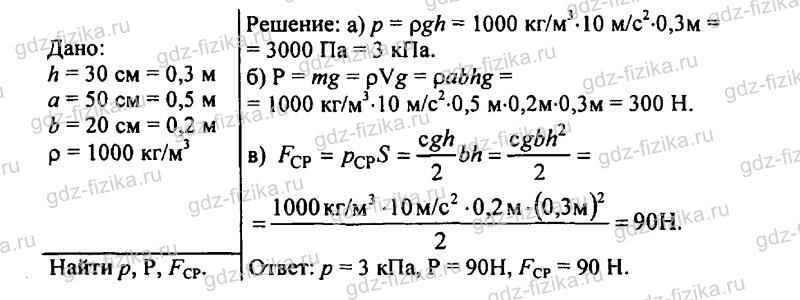
524. Ширина шлюза 10 м. Шлюз заполнен водой на глубину 5 м. С какой силой давит вода на ворота шлюза?
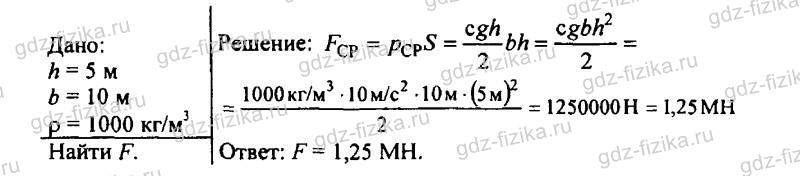
525. В цистерне, заполненной нефтью, на глубине 3 м имеется кран, площадь отверстия которого 30 см2. С какой силой давит нефть на кран?

526. Прямоугольный сосуд вместимостью 2 л наполовину наполнен водой, а наполовину керосином, а) Каково давление жидкостей на дно сосуда? б) Чему равен вес жидкостей в сосуде? Дно сосуда имеет форму квадрата сo стороной 10 см.

527. Определите силу, с которой действует керосин на квадратную пробку площадью поперечного сечения 16 см2, если расстояние от пробей до уровня керосина в сосуде равно 400 мм (рис. 141).

528. Какую силу испытывает каждый квадратный метр площади поверхности водолазного костюма при погружении в морскую воду на глубину 10 м?
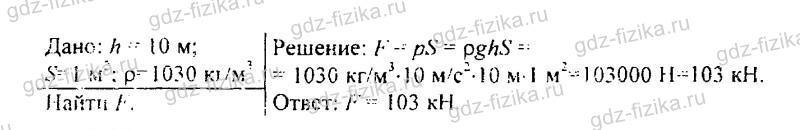
529. Плоскодонная баржа получила пробоину в дне площадью 200 см2. С какой силой нужно давить на пластырь, которым закрывают отверстие, чтобы сдержать напор воды на глубине 1,8 м? (Вес пластыря не учитывать.)
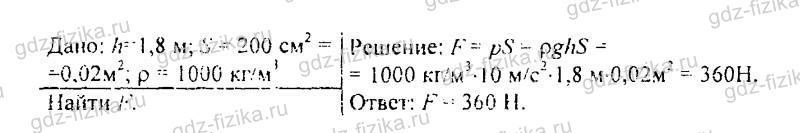
530. Определите высоту уровня воды в водонапорной башне, если манометр, установленный у ее основания, показывает давление 220000 Па.
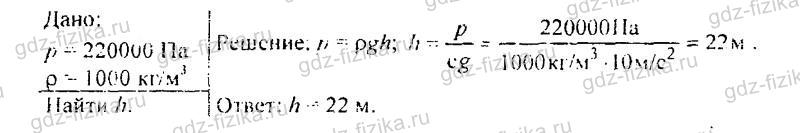
531. На какой глубине давление воды в море равно 412 кПа?
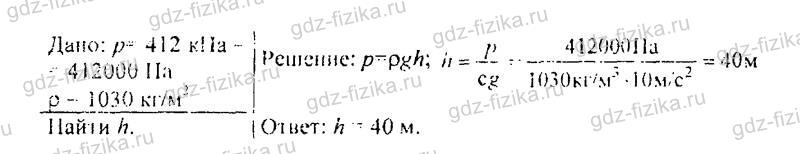
532. Напор воды в водокачке создается насосом. Определите на какую высоту поднимается вода, если давление, созданное насосом, равно 400 кПа?
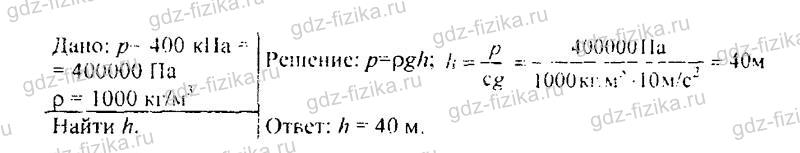
533. Брусок размером 0,5×0,4×0,1 м находится в баке с водой на глубине 0,6 м (рис. 142). Вычислите: а) с какой силой вода давит на верхнюю грань бруска; б) на нижнюю грань бруска; в) сколько весит вода, вытесненная бруском.
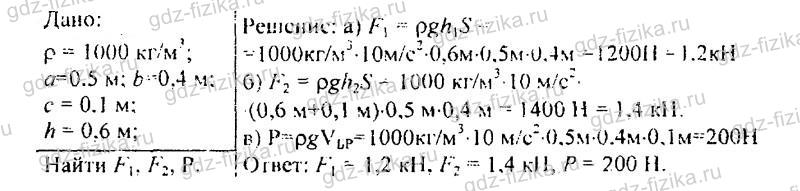
534. Произведите расчет, взяв данные предыдущей задачи, предполагая, что воду заменили керосином.
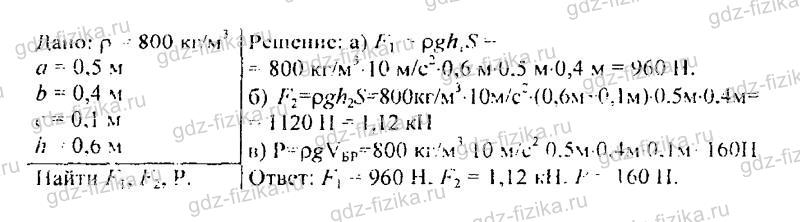
535. Используя результаты двух предыдущих задач, вычислите, на сколько сила, действующая на тело снизу, больше силы, действующей на тело сверху: а) в воде; б) в керосине. Сравните полученные результаты с весом вытесненной воды и с весом вытесненного керосина.

536. Один из кофейников, изображенных на рисунке 143, вмещает больше жидкости, чем другой. Укажите какой и объясните.
Правый кофейник вмещает больше жидкости, чем левый, гак как у него кончик носика находится выше.
537. Точкой А обозначен уровень воды в левом колене трубки (рис. 144). Сделайте рисунок и на нем отметьте точкой В уровень воды в правом колене трубки.

538. В сообщающиеся сосуды налита вода. Что произойдет и почему, если в левый сосуд долить немного воды (рис. 145); в средний сосуд долить воды (рис. 146)?
Уровень воды увеличится во всех сосудах на одинаковую высоту. Таким образом, уровни снова выравнятся (рис. 145, 146).
539. Справедлив ли закон сообщающихся сосудов в условиях невесомости? Объясните почему.
Закон сообщающихся сосудов в условиях невесомости не действует, так как жидкости в состоянии невесомости не обладают весом и потому не оказывают давления на дно сосудов.
540. Как при помощи сообщающихся сосудов проверить, горизонтально ли нанесена филенка (линия, отделяющая окраску панели от верхней части стены)?
Нужно взять длинную тонкую резиновую трубку, вставить стеклянные трубки на концах, залить эту систему водой, а концы стеклянных трубок подвести к филенке. Используя свойство сообщающихся сосудов, пройтись с одной из стеклянных трубок вдоль стены.
541. Объясните действие фонтана (рис. 147).
Действие фонтана объясняется тем, что давление жидкости в верхнем конце правой трубки будет больше атмосферного, так как уровень воды в этой трубке меньше уровня воды в левой трубке.
542. В левом колене сообщающихся сосудов налита вода, в правом — керосин (рис. 148). Высота столба керосина 20 см. Рассчитайте, на сколько уровень воды в левом колене ниже верхнего уровня керосина.
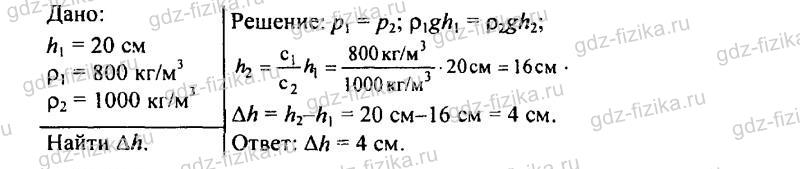
543. В сообщающихся сосудах находятся ртуть и вода (рис. 149). Высота столба воды 68 см. Какой высоты столб керосина следует налить в левое колено, чтобы ртуть установилась на одинаковом уровне?

544. В сообщающихся сосудах находилась ртуть. Когда в правую трубку налили слой керосина высотой 34 см, то уровень ртути в левой трубке поднялся на 2 см. Какой высоты следует налить слой воды в левую трубку, чтобы ртуть в трубках установилась на одинаковом уровне (рис. 149)?
545. В сообщающихся сосудах находятся ртуть, вода и керосин (рис. 150). Какова высота слоя керосина, если высота столба воды равна 20 см и уровень ртути в правом колене ниже, чем в левом, на 0,5 см?

Источник

