В дне сосуда отверстие
В сечении /—I геометрический напор 2] = Я, а в сечении I]—II напор 22 = 0. Сосуд открыт, истечение через отверстие происходит в пространство с атмосферным давлением следовательно, р = р2. Скоростью в поперечном сечении сосуда, по сравнению со скоростью в отверстии, можно пренебречь, т. е. принять w = 0. Сделав соответствующие подстановки и сокращения в уравнении (6-28), получим [c.164]
Формулы (6-73) и (6-76) могут быть применены при расчете истечения через отверстие в стенке, разделяющей два сосуда, причем в данном случае Н представляет собой разность постоянных уровней жидкости в сосудах. [c.166]
ИСТЕЧЕНИЕ ЧЕРЕЗ ОТВЕРСТИЯ И НАСАДКИ ПРИ ПЕРЕМЕННОМ НАПОРЕ (ОПОРОЖНЕНИЕ СОСУДОВ) [c.134]
Истечение через отверстие в дне сосуда при постоянном уровне жидкости к сосуде, В этом случае (рис. 10) сила напора И затрачивается на создание скорости истечения Шд жидкости и преодоление сопротивления в отверстии. Если эго сопротивление отсутствует, т. е. происходит истечение идеальной жидкости, то согласно уравнению Бернулли весь статический напор в отверстии переходит в скоростной [c.48]
Величина коэффициента сжатия зависит от характера сжатия, которое бывает полным и неполным, совершенным и несовершенным. Сжатие называется совершенным, если оно наблюдается при истечении через отверстия в тонком плоском дне, при котором боковые стенки сосуда влияния на сжатие не оказывают. Последнее имеет место, если стенки расположены на расстоянии с от отверстия, не меньшем утроенной длины соответствующей стороны отверстия (рис. 1.65,1). [c.66]
Истечение через отверстие в дне сосуда [c.203]
Задача анализа — определение массового расхода газа G при стационарном его истечении через отверстие, сопло или насадок из сосуда с повышенным давлением в газовую среду с более низким. [c.209]
Скорость истечения зернистой среды через отверстие сосуда так же, как и при истечении жидкостей, определяется нормальным давлением над плоскостью, нормальной к направлению потока материала в зоне течения [c.434]
При вибрировании тиксотропных влажных паст наблюдается их истечение через отверстия в дне сосуда, подобно тому как вытекает вязкая жидкость под гидростатическим давлением. [c.157]
Расчетная формула для расхода жидкости при истечении через отверстие в днище сосуда будет иметь вид [c.83]
Уменьшение объема жидкости в левом сосуде будет равно расходу ее при истечении через отверстие, расположенное между сосудами. Можно написать [c.84]
При истечении через отверстие в боковой стенке (см. рис. 6-19,6) напор не будет одинаковым для всех точек по сечению отверстия и уравнения (6-71) и (6-72), строго говоря, будут применимы только для элемента сечения высотой йН. В этом случае расход жидкости может быть точно определен только путем суммирования, т. е. интегрирования элементарных расходов по всему сечению отверстия. Однако в технических расчетах для отверстия в тонкой боковой стенке можно с достаточной точностью пользоваться теми же расчетными уравнениями, что и для отверстия в дне сосуда. Лишь для отверстий больших размеров следует учитывать изменения коэффициентов расхода, значения которых приводятся в справочниках. [c.166]
Однако в технических расчетах истечения через отверстие в тонкой боковой стенке можно с достаточной точностью пользоваться теми же расчетными уравнениями, что и при истечении через отверстие в дне сосуда. [c.58]
Теперь рассмотрим истечение через отверстие в тонком днище при переменном уровне жидкости в сосуде с целью определения времени опорожнения сосудов. [c.65]
Заключив в замкнутый сосуд образец какого-либо газа, мы можем измерить его массу, объем, давление на стенки сосуда, вязкость, температуру, теплопроводность и скорость распространения в нем звука. Легко также измерить скорость эффузии (истечения) газа через отверстие в сосуде и скорость, с которой один газ диффундирует в другой. В данной главе будет показано, что все эти свойства не являются независимыми друг от друга, а связаны при помощи довольно простой теории, основанной на предположении, что газы состоят из непрерывно движущихся и сталкивающихся частиц. [c.114]
При выгрузке через отверстие в стенке или дне сосуда псевдоожиженный материал принимает форму струи. Последняя на выходе из отверстия очень похожа на струю капельной жидкости независимо от агрегатного состояния ожижающего агента (газ или жидкость). Струи материала наблюдаются и при гравитационном движении массы твердых частиц через горизонтальные отверстия в дне бункеров, содержащих сухие сыпучие материалы. Известно, однако, что через отверстия в боковой стенке сосуда горизонтальное движение твердого материала в последнем случае практически отсутствует и струя никогда не образуется. У псевдоожиженных систем.на уровне отверстия поддерживается гидростатический напор, способствующий горизонтальному движению зернистого материала и выгрузке его из аппарата. Условия экспериментального исследования процесса истечения псевдоожиженных систем приведены в табл. XV-1. [c.568]
Сыпучесть является комплексной характеристикой способности материала образовывать дискретно-непрерывный устойчивый поток. Простейший способ экспериментального определения сыпучести состоит в определении максимальной скорости свободного истечения материала из сосуда через отверстие определенного диаметра. [c.47]
Рассмотрим истечение жидкости из открытого сосуда (рис. И-14), имеющего площадь поперечного сечения Р и донное отверстие площадью Ро. За бесконечно малый промежуток времени йТ через отверстие вытечет объем жидкости 0 , равный [c.58]
В отличие от истечения жидкостей из сосудов движение сыпучих материалов происходит неравномерно по поперечному сечению бункера, в результате этого в центре образуется воронка, постепенно достигающая стенок аппарата. В дальнейшем по мере разгрузки материала через нижнее отверстие стенки воронки обрушиваются. Среднюю скорость истечения сыпучего материала из отверстия бункера можно рассчитать по приближенному уравнению [c.360]
Расход и скорость истечения несжимаемой жидкости через отверстие в дне сосуда, при постоянном уровне Я (рис. 1-12) и постоянных давлениях р> [c.403]
Истечение жидкостей. Определим расход жидкости при ее истечении через круглое отверстие в тонком днище открытого сосуда, в котором поддерживается постоянный уровень Н жидкости (рис. П-20, а). [c.61]
Сжатие струи имеет место из-за наличия инерции газовых струй при входе в отверстие или сопловой канал. Нанбольшее сжатие происходит при истеченпп через выступающую внутрь сосуда тонкостенную трубу. В случае истечения через отверстие с острыми краями коэффициент сжатия е = 0,60- 0,62. [c.202]
Закон Грема. При равных давлениях скорости истечения газов из не1больШ Их отверстий (только при истечении через отверстия тонкостенных шайб или сосудов, когда не сказываются силы трения) обратно пропорциональны корням квадратным из их плотностей [c.83]
Сосуд с водой взвешивают и, вычитая из полученного веса вес пустого цилиндра, находят количество воды. После того как на приборе будет закрыт клапан 5 и левая кнопка перекидных рычагов поставлена до упора в верхнее положение, прибор может быть использован для последующей работы. Измерение с воздухом повторяют три раза и для расчета принимают среднее значс ние. Количество воды, протекающей за время, одинаковое со временем истечения через отверстие испытуемого газа, определяют аналогичным путем, за исключением того, что газоподводящую трубку 2 подключают к источнику анализируемого газа, продувают прибор и наполняют колокол газом, находящимся под давлением в газопроводе. [c.124]
В тех случаях, когда отверстие настолько велико, что газ гидродинамически вытекает из него сплошной струей. Но если условия истечения газа таковы, что через отверстие в сосуде способны проходить только изолированные молекулы, совершающие беспорядочные движения в стационарном газе, предсказания молекулярно-кинетической теории вьшолн5потся точно. [c.149]
Аппарат Энглера был несколько видоизменен Уббелоде (357), снабдившим его более длинной и узкой трубкой истечения. Этот вариант пригоден для определения вязкости очень подвижных масел. Отличие от аппарата Эш лера состоит в том, что наблюдается скорость истечения только 100 см наполнение сосуда А (фиг. 53) производится автоматически до некоторого уровня, определяемого отводной трубкой d. Для более густых жидкостей, чем керосин, даже для тех, вязкость которых хорошо оиределяется энглеровским прибором, видоизменение Уббелоде дает, вообш е говоря, более точные-цифры. Настояш,ая область применения аппарата—определение вязкости лри температурах выше 50°. Уббелоде предложил еще один вариант вискозиметра, в котором постоянная температура иоследуемого масла поддерживается парами какой-нибудь кипящей однородной жидкости (анилин, нитробензол и т. п.). Рубашка, окружающая сосуд с маслом, закрыта наглухо в крьипке ее имеется отверстие для наливания жидкости и другое для обратного холодильника. Потеря через лучеиспускание происходит только через крышку сосуда с маслом, которая изолируется дурными проводниками тепла. [c.255]
Движение псевдоожиженных твердых частиц может происходить через отверстия в стенках аппарата или по вертикальным трубам, связывающим его с рядом стоящими аппаратами. В зависимости от того, происходит ли истечение из отверстий в свободное пространство или в другие псевдоожиженные слои, говорят о свободном или затопленном истечении. Во втором случае два соседних слоя могут находиться в общем сосуде частицы и газ будут перераспределяться между слоями в соответствии с перепадом давлений, устанавливающимся в зависимости от высоты слоев по разные стороны разделяющей перегородки. При движении плотной фазы твердых частиц по вертикальным трубам, связанным с аппаратами для псевдоожижения, мы имеем дело с движущимися псевдоожиженными системами их результирующая скорость относительно стенок сосуда отлична от нуля, а перепад давления — постоянен. Примеры движения псевдоожиженной плотной фазы через отверстия или по вертикальным трубам легко найти в нефтеперерабатывающей промыш.ген-ности циркуляция катализатора между реактором и регенераторо.ч в установках каталитического крекинга. [c.568]
Истечение из отверстия в дне сосуда при постоянном напоре. На рис.4.11 представлен сосуд с отверстием в горизонтальнои дне, через которое вытекает жидкость. Давление над уровнем жидкости в сосуде ран/м , давление среды, в которую происхс-дит истечение, рн/м . Расстояние от произвольно взятой плоскости сравнения х—х до уровня а—Ь жидкости в сосуде — го л. то же до сечения с—с( иа уровне отверстия — г м. [c.128]
Смотреть страницы где упоминается термин Истечение через отверстие в дне сосуда:
[c.77]
[c.164]
Источник
Закон Торричелли
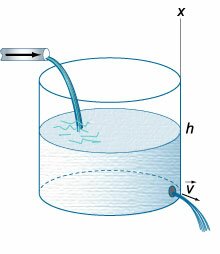
Итальянский ученый Эванджелиста Торричелли, изучавший движение жидкостей,
в (1643) году экспериментально обнаружил, что скорость вытекания жидкости через малое отверстие на дне открытого сосуда (рисунок (1)) описывается формулой:
[v = sqrt {2gh} ,]
где (h) − высота уровня жидкости над отверстием, (g) − гравитационная постоянная.
|
|
Рис.1 | Рис.2 |
Такая же формула описывает скорость тела, свободного падающего с высоты (h) в поле тяжести Земли в вакууме.
В действительности, найденная формула не совсем точна. В более точном приближении скорость жидкости зависит от формы и размера отверстия, от вязкости жидкости и режима течения. Поэтому,
формула Торричелли часто записывается с дополнительным множителем (varphi:)
[v = varphisqrt {2gh} ,]
где коэффициент (varphi) близок к (1.) Значения параметра (varphi) для отверстий различной формы и размера можно найти в гидравлических справочниках.
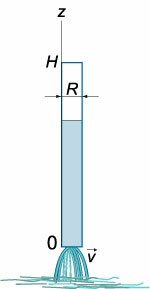
Вытекание жидкости из тонкой трубки
Вытекание жидкости из тонкой длинной трубки (рисунок (2)) имеет ряд особенностей. Здесь важную роль играют капиллярные эффекты, обусловленные
поверхностным натяжением и смачиванием вследствие контакта со стенками трубки.
Скорость вытекания жидкости из капиллярных трубок приблизительно пропорциональна высоте столба жидкости над отверстием, то есть
[v = kh,]
где (k) − некоторая константа, зависящая от вязкости жидкости, геометрии и материала трубки.
Далее мы будем описывать вытекание жидкости с помощью дифференциальных уравнений из сосудов обоих типов (широкого и тонкого).
Дифференциальное уравнение вытекания жидкости
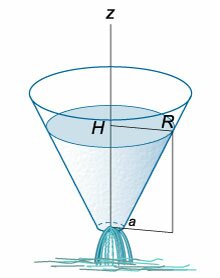
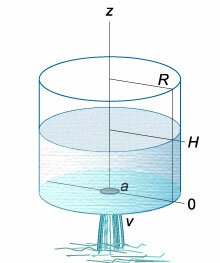
Данное дифференциальное уравнение можно вывести, рассматривая баланс жидкости в сосуде. Возьмем, например, цилиндрический сосуд с широким основанием, радиус
которого равен (R.) Предположим, что жидкость вытекает через малое отверстие радиуса (a) на дне сосуда (рисунок (3)).
|
|
Рис.3 | Рис.4 |
Скорость жидкости описывается формулой Торричелли:
[v = sqrt {2gz} ,]
где (z) − высота жидкости над отверстием. Тогда поток жидкости определяется выражением:
[q = – pi {a^2}sqrt {2gz} .]
Здесь (pi {a^2}) соответствует площади отверстия, через которое вытекает жидкость, а знак “минус” означает,
что уровень жидкости уменьшается по мере ее вытекания из резервуара.
Уравнение баланса жидкости в резервуаре описывается следующим образом:
[frac{{dV}}{{dt}} = q.]
Поскольку изменение объема (dV) можно выразить как
[dV = Sleft( z right)dz,]
то мы получаем дифференциальное уравнение
[frac{{Sleft( z right)dz}}{{dt}} = qleft( z right).]
Подставим функцию (qleft( z right)) в это уравнение:
[frac{{Sleft( z right)dz}}{{dt}} = – pi {a^2}sqrt {2gz} .]
Поперечное сечение ({Sleft( z right)}) цилиндрического сосуда не зависит от высоты (z) и равно
[Sleft( z right) = pi {R^2},]
где (R) − радиус основания цилиндра. Тогда
[require{cancel}
cancel{pi} {R^2}frac{{dz}}{{dt}} = – cancel{pi} {a^2}sqrt {2gz} .
]
В результате получаем уравнение с разделяющимися переменными:
[frac{{dz}}{{sqrt z }} = – frac{{{a^2}}}{{{R^2}}}sqrt {2g} dt.]
Теперь проинтегрируем полученное уравнение, считая, что начальный уровень жидкости составляет (H,) и за время (T) он уменьшается до (0:)
[
{intlimits_H^0 {frac{{dz}}{{sqrt z }}} = – intlimits_0^T {frac{{{a^2}}}{{{R^2}}}sqrt {2g} dt} ,};;
{Rightarrow 2left[ {left. {left( {sqrt z } right)} right|_H^0} right] = – frac{{{a^2}}}{{{R^2}}}sqrt {2g} left[ {left. {left( t right)} right|_0^T} right],};;
{Rightarrow 2sqrt H = frac{{{a^2}}}{{{R^2}}}sqrt {2g} T,};;
{Rightarrow sqrt {2H} = frac{{{a^2}}}{{{R^2}}}sqrt g T.}
]
Отсюда следует выражение для полного времени вытекания жидкости (T:)
[T = frac{{{R^2}}}{{{a^2}}}sqrt {frac{{2H}}{g}} .]
Интересно, что в предельном случае (a = R) (когда площади отверстия и самого цилиндра равны), полученная
формула преобразуется в известную формулу (T = sqrt {largefrac{{2H}}{g}normalsize}, )
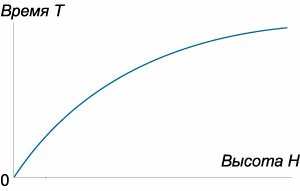
которая определяет время падения материального тела с высоты (H.) Зависимость времени (T) от высоты (H) схематически показана на рисунке (4.)
Аналогично можно описать вытекание жидкости и из сосуда другой формы.
Вывести дифференциальное уравнение вытекания жидкости из конического сосуда и определить полное время вытекания (T.)
Радиус верхнего основания конического сосуда равен (R,) а радиус нижнего основания (a.) Начальная уровень жидкости составляет (H) (рисунок (5)).
|
|
Рис.5 | Рис.6 |
Изменение уровня жидкости на высоте (z) описывается дифференциальным уравнением
[Sleft( z right)frac{{dz}}{{dt}} = qleft( z right),]
где (Sleft( z right)) − площадь поперечного сечения сосуда на высоте (z,) а (qleft( z right)) − поток жидкости, зависящий от высоты (z.)
Принимая во внимание геометрию сосуда, можно предположить, что закон Торричелли выполняется. Поэтому, можно записать:
[qleft( z right) = – pi {a^2}sqrt {2gz} ,]
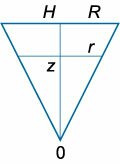
где (a) − радиус отверстия на дне конического сосуда. Учитывая, что отверстие достаточно малое, осевое сечение можно рассматривать как треугольник
(рисунок (6) выше). Из подобия треугольников следует, что
[frac{R}{H} = frac{r}{z}.]
Следовательно, площадь поверхности жидкости на высоте (z) будет равна
[
{Sleft( z right) = pi {r^2} }
= {pi {left( {frac{{Rz}}{H}} right)^2} }
= {frac{{pi {R^2}{z^2}}}{{{H^2}}}.}
]
Подставляя (Sleft( z right)) и (qleft( z right)) в дифференциальное уравнение, имеем:
[frac{{pi {R^2}{z^2}}}{{{H^2}}}frac{{dz}}{{dt}} = – pi {a^2}sqrt {2gz} .]
После простых преобразований получаем следующее дифференциальное уравнение:
[{z^{largefrac{3}{2}normalsize}}dz = – frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} dt.]
Проинтегрируем обе части, учитывая, что уровень жидкости уменьшается от начального значения (H) до нуля за время (T:)
[
{intlimits_H^0 {{z^{largefrac{3}{2}normalsize}}dz} = – intlimits_0^T {frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} dt} ,};;
{Rightarrow left. {left( {frac{{{z^{largefrac{5}{2}normalsize}}}}{{frac{5}{2}}}} right)} right|_0^H = frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} left[ {left. {left( t right)} right|_0^T} right],};;
{Rightarrow frac{2}{5}{H^{largefrac{5}{2}normalsize}} = frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} T,};;
{Rightarrow frac{1}{5}sqrt {frac{{2H}}{g}} = frac{{{a^2}}}{{{R^2}}}T,};;
{Rightarrow T = frac{{{R^2}}}{{5{a^2}}}sqrt {frac{{2H}}{g}} .}
]
Здесь мы снова видим аналогию с падением материального тела с высоты (H) в гравитационном поле Земли. Как известно,
время падения описывается формулой:
[T = sqrt {frac{{2H}}{g}}. ]
Если мы сравним этот результат со случаем вытекания жидкости из цилиндрического сосуда, то видно, что при тех же самых
значениях (H, R) и (a) время вытекания жидкости из конического сосуда ровно в (5) раз меньше, чем из цилиндра (хотя
объем конического сосуда меньше лишь в (3) раза!). Такие целочисленные отношения в природе выглядят удивительными, не правда ли?
Исследовать вытекание жидкости из тонкой трубки радиусом (R) и высотой (H,) считая трубку полностью заполненной жидкостью.
|
|
Рис.7 | Рис.8 |
Аналогично разобранным выше примерам, мы можем записать уравнение баланса жидкости на некоторой произвольной высоте (z) в следующей форме:
[Sleft( z right)frac{{dz}}{{dt}} = qleft( z right).]
В данном случае площадь поперечного сечения (Sleft( z right)) является константой:
[Sleft( z right) = S = pi {R^2},]
и поток жидкости, вытекающей из сосуда, определяется формулой:
[qleft( z right) = – kz,]
где (k) зависит от размера отверстия, смачиваемости и других параметров.
В результате получаем простое дифференциальное уравнение:
[pi {R^2}frac{{dz}}{{dt}} = – kz,]
или после разделения переменных:
[frac{{dz}}{z} = – frac{k}{{pi {R^2}}}dt.]
Теперь это уравнение можно проинтегрировать, считая, что уровень жидкости уменьшается с высоты (H) до (h) за время от (0) до (t:)
[
{intlimits_H^h {frac{{dz}}{z}} = – intlimits_0^t {frac{k}{{pi {R^2}}}dt} ,};;
{Rightarrow left. {left( {ln z} right)} right|_h^H = frac{k}{{pi {R^2}}}t,};;
{Rightarrow t = frac{{pi {R^2}}}{k}left( {ln H – ln h} right) = frac{{pi {R^2}}}{k}ln frac{H}{h}.}
]
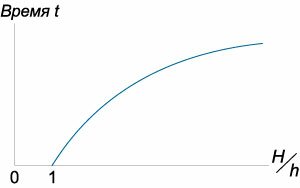
Зависимость времени (t) от отношения (largefrac{H}{h}normalsize) показана схематически на рисунке (8.)
Данная кривая аналогична зависимости времени (T) от высоты (H) для широкого цилиндрического сосуда, для которого справедлив закон Торричелли.
Интересно, что в данной простой модели время вытекания жидкости (t) формально стремится к бесконечности при (h to 0.)
Источник